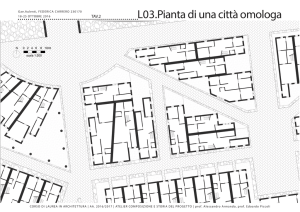
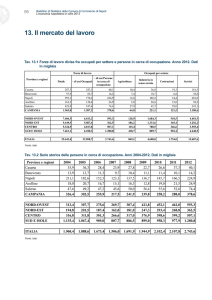
/
/
'
-~~~~~~---~
IUAV' VENEZIA
AREA SERV. BIBLIOGRAFICI
E DOCUMENTALI
DEPCIA
w
287
luigi brasca
prontuario
,·'~ per calcoli finanziari
e attuariali a cura di eugenio levi e cesare brasca
'1
27a edizione
ghisetti e corvi editori
ii
g/Slc
m
< -m
Zi r-
E
o
-t
o
m
;;;;
(")
'
)>
1""'
j·~
~
(/)
(10 ...
~
()r.;i
'C7
tl1
~ \)
f ";
INDICE SISTEMATICO
Indice analitico ................................................... pag.
Sommario dei Chiarimenti (§§ 53 - 6 I) . . . . . . . . . . . . . . . . . . . . • . . . . . . . . . . . »
11
14
Parte prima
INTERESSE E SCONTO SEMPLICE
Tav.
»
»
»
I. Interesse semplice di una lira (anno civile) . .................
»
»
» »
» (anno commerciale) ...........
2.
3. Divisori fissi e moltiplicandi fissi
4. Valore attuale di una lira esigibile dopo g giorni (sconto razionale)
..........................
»
»
»
»
16
18
20
22
»
»
26
28
30
34
54
78
Parte seconda
INTERESSE E SCONTO COMPOSTO
Tav. 5.
»
6.
»
7.
»
8.
»
9.
» 10.
Interesse composto di una lira, per giorni . . . . . . . . . . . . . . . . . .
Montante di una lira dopo m mesi. . . . . . . . . . . . . . . . . . . . . . . . .
Valore attuale di una lira esigibile dopo m mesi . . . . . . . . . . . .
Montante di una lira dopo n anni. - Valori di (1
i)n . . . . .
Valore attuale di una lira esigibile dopo n anni. - Valori di vn. . .
Tempo necessario perchè un capitale divenga multiplo di se stesso
+
»
»
»
»
Parte terza
TASSI EQUIVALENTI
Equivalenze fra tassi posticipati
Tav. 11. Tassi equivalenti: a) valori di ik, dato i
))
))
» 12.
b) valori di Ìk· dato i
)) 13.
: c) valori di i, dato Ìk
»
»
...................
...................
...................
Equivalenze fra tassi anticipati e tassi
e viceversa
))
))
80
83
84
posticipati.~
Tav. 14. Tassi equivalenti: d) valori di i, dato ia (interesse semplice)
))
))
»
: e) valori di ia, dato i (interesse semplice)
15.
(~ »
))
»
: /) valori di i, dato ia (interesse composto)
16.
tl
/
»
))
»
»
86
88
90
7
Parte quarta
VERSAMENTI PERIODICI
J
Tav. 17. Montante della rendita unitaria. - Valori di 6nii ••••...•.••• pag.
»
18. Valore attuale della rendita unitaria immediata. - Valori di Unii. »
»
19. Rata annua posticipata di ammortamento del debito di una lira. Valori di cxnii • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • »
»
20. Rata annua anticipata di ammortamento del debito di una lira. Valori di Oinii • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • »
»
21. Rata annua posticipata per la costituzione del capitale di una lira
dopo n anni. - Valori di ami .•.......... • .. · . · · · · · · • · · · · · »
22. Rata annua anticipata per la costituzione del capitale di una lira
»
dopo n anni. - Valori di crnii •.....•.......... · · · · · · · · · · · · »
» 23. Fattore di correzione per rendite frazionate:
a) a rate posticipate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . »
b) a rate anticipate. . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . »
» 24. Rata per la costituzione del capitale di una lira dopo un anno,
a interesse semplice:
a) rata posticipata....................................
b) rata anticipata . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . »
» 25. Rata per la costituzione del capitale di una lira dopo un anno,
a interesse composto:
a) rata posticipata. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . »
b) rata anticipata . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . »
26. Rata semestrale posticipata di ammortamento del debito di una
»
»
94
112
134
162
166
170
174
175
178
179
180
181
»
»
186
188
....................................
»
29. Valori di Log 6nii· ••• • • • • • • • • • • • • .. • • • • • • • • • • • • • • • • • • • • • • •
30. Valori di Log ami ...•....... • · · · • • • • · · • · • • · · • · · · · · · · · · • · ·
»
»
ì 94
198
202
»
»
»
»
208
210
212
214
lira. - Valori di cxnii • i 2/i ......... · · · · · · · · · · · · · · · · · · · · · · · ·
27. Piani di ammòrtamento (metodo progressivo o francese) . . . . .
Parte quinta
LOGARITMI DEI VALORI
DELLE FUNZIONI FINANZIARIE
Tav. 28. Valori di Log (1
»
»
+ ir
Parte sesta
TAVOLE ATTUARIALI
Tav. 31. S.I. m 1901 - Tavola di sopravvivenza e demografico-finanziaria 4% . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
» 32. Italia m 1950-53 Tavola di sopravvivenza . . . . . . . . . . . . . . .
»
33. Italia f 1950-53 »
»
»
»
»
»
»
34. Italia mf 1950-53 -
8
Tav. 35. Italia m 1950-53 - Tavola demografico-finanziaria 4%:
a) valori dei simboli di commutazione e loro logaritmi ... pag.
b) valori di ax, Àx, Px, lfiix ............. ~........... »
» 36. Italia m 1960-62 Tavola di sopravvivenza . . . . . . . . . . . . . . . »
»
» 37. Italia { 1960-62 »
»
»
»
»
»
»
»
38. Italia mf 1960-62 » 39. Italia m 1960-62 - Tavola demografico-finanziaria 4%:
a) valori <lei simboli di commutazione e loro logaritmi . . »
b) valori di ax, Àx, Àx, Px, Px, lfiix . . . . . . . . . . . . . . . . »
» 40. Italia m 1970-72 - Tavola di sopravvivenza . . . . . . . . . . . . . . . »
» 41. Italia f 1970-72 »
»
»
............... »
» 42. Italia mf 1970-72 »
»
»
............... »
» 43. Italia m 1970-72 - Tavola demografico-finanziaria 4%:
a) valori dei simboli di commutazione e loro logaritmi . . »
b) valori di ax, Àx, Àx, Px, Px, l/iix . . . . . . . . . . . . . . . . »
» 44. S.I. mf 1931 - Usufrutto vitalizio e nuda proprietà . . . . . . . . .
»
» 45. Italia m 1970-72 - Valore attuale della rendita vitalizia
»
» 46. Italia f 1970-72 »
»
»
»
»
»
216
220
222
224
226
228
232
234
236
238
240
244
246
248
249
Parte settima
TAVOLE ARITMETICHE
Tavole numeriche
1
1
. ; n,
- v.a;Tav. 47. Valori di n, n a, v
n, . 1.000, rm, - n;n 2
n
4
•
•
2
»
252
»
»
272
273
276
»
280
.......
»
»
»
»
284
286
288
290
Tav. 56. Conversione dal sistema decimale al sistema binario . . . . . . . . .
»
290
»
»
»
»
»
292
292
293
296
332
»
»
»
»
48. Valori di n 4 , n 5, n 6 • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
49. Numeri primi compresi fra 1 e 10.000......................
50. Scomposizione in fattori primi dei numeri da 1 a 1.000 . . . . . . . .
51.
»
»
»
»
»
»
da 1.001 a 10.000, non
divisibili per 2, 3, 5, 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
»
Tavole di decimalizzazione
Tav.
»
»
»
52.
53.
54.
55.
Conversione di frazioni in numeri decimali .................
Conversione di giorni in decimali di anno (anno civile) . ......
Conversione di giorni e mesi in decimali di anno (anno commerciale)
Conversione di minuti e secondi in decimali di grado
Tavola di conversione al sistema binario
Parte ottava
TAVOLE LOGARITMICHE
Tav. 57. Trasformazione di logaritmi decimali in neperiani e viceversa.
» 58. Costanti e loro logaritmi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . • .
» 59. Mantisse dei logaritmi dei numeri da 1 a 1.000 . . . . . . . . . . . . .
» 60. Mantisse dei logaritmi dei numeri da 1.000 a 10.000 . . . . . . . .
» 61. Ma~1tisst\'.a 7 decimali) dei logaritmi dei numeri da 10.000 a 11.500
I
9
/
APPENDICE
Tav. 62. Giorni.. trascorsi dal principio dell'anno ..................... pag.
» 63. Giorni mancanti alla fine dell'anno . . . . . . . . . . . . . . . . . . . . . . . . »
» 64. Coefficienti binomiali, fattoriali e numeri d'uso frequente
»
»
65. Curva normale standard di probabilità. - Valori di f(z) • . . . »
»
66.
»
»
»
»
»
- Valori di F(z) . . . . »
» 67. Potenze del numero e. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . »
» 68. Tavole di ragguaglio:
a) delle unità di misura del sistema inglese . . . . . . . . . . . . »
b) delle unità di misura del sistema U.S.A. . . . . . . . . . . . . »
e) delle unità di misura agrarie locali italiane. . . . . . . . . . . »
» 69. Conversione di misure inglesi in misure del sistema metrico decimale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . »
344
345
346
348
349
350
352
353
354
354
AVVERTENZE PER L'USO DELLE TAVOLE
E CHIARIMENTI DIVERSI
Osservazioni sugli arrotondamenti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Nota sull'interpolazione lineare e sull'approssimazione dei risultati con
essa ottenibili . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Avvertenze per l'uso delle tavole (§§ 1-52) .. .. .. .. .. .. .. .. .. .. .. .. ..
Chiarimenti riguardanti la risoluzione di problemi che implicano l'uso
della matematica finanziaria (§§ 53-64) (o) . . . . . . . . . . . . . . . . . . . . . . .
Riepilogo delle formule finanziarie fondamentali . . . . . . . . . . . . . . . . . . . . .
(0)
10
Ved. Sommario a pag. 14.
»
355
»
»
356
358
»
406
414
»
INDICE
ANALITICO
Ammortamento di un debito: ved. Rata
di ammortamento. e Piani di ammortamento
Antilogaritmo, § 42
Approssimazione ottenibile con l'interpolazione lineare, pag. 356
Arrotondamento, pag. 355
Base dei logaritmi, § 39
cambiamento di base dei logaritmi, § 45
Capitalizzazione continua, §§ 51, 10 e 13
Capitalizzazione frazionata (semestrale,
trimestrale, ecc.), § 8
Caratteristica di un logaritmo decimale,
§ 40
Coefficienti binomiali, tav. 64, § 49
Cologaritmo, §§ 39 e 41
Conversione:
di frazioni in numeri decimali, tav. 52,
§ 37
di giorni in decimali di anno (anno
civile), tav. 53
di giorni e mesi in decimali di anno
(anno commerciale), tav. 54
di minuti e secondi in decimali di grado,
tav. 55
dal sistema decimale al sistema binario,
tav. 56, § 38
di misure inglesi in misure del sistema
metrico decimale, tav. 69, § 52
Costituzione di un capitale: ved. Rata di
costituzione di un capitale
Costo effettivo di un prestito:
ammortizzabile mediante rate annue
costanti, §§ 61 e 63
ammortizzabile mediante rate semestrali, trimestrali, ecc. costanti, §§
59 e 62
Criterio del minimo errore (nell'arrotondamento), pag. 355
Cubi dei numeri interi, tav. 47
Curva di Gauss, § 50
Curva normale standard di probabilità:
area sottostante alla curva [F(z)], tav.
66, § 50
ordinata della. curva [f(z)], tav. 65,
I~
§ 50
il
/
Decimalizzazione di frazioni, tav. 52, § 37
Distribuzione normale di probabilità, § 50
Divisori fissi, tav. 3, § 2
e (numero), § 46
potenze di e, tav. 67, § 51
Fattore di correzione per rendite frazionate:
a rate semestrali, trimestrali, ecc. posticipate: tav. 23, a; § 19
a rate semestrali, trimestrali, ecc. anticipate: tav. 23, b; § 19
Fattoriali, tav. 64, § 49
Formule :finanziarie fondamentali (riepilogo), pag. 414, § 25
Frequenza, § 50
Gauss (curva di), § 50
Giorni mancanti alla fine dell'anno, tav.
63, § 48
Giorni trascorsi dal principio dell'anno,
tav. 62, § 48
Interesse composto, per giorni, tav. 5, § 5
(ved. anche Montante)
Interesse semplice:
con l'anno civile, tav. 1, § 1
con l'anno commerciale, tav. 2, § 1
Interpolazione lineare (approssimazione
dei risultati con essa ottenibili), pag.
356
Leasing, § 60
Logaritmi:
decimali (o in base 10): tav. 59, 60 e 61;
§§ 40 e 41
neperiani (o naturali, o in base e), § 46
base dei lÒgaritmi, § 39
calcolo dei logaritmi decimali,§§ 40 e 41
cambiamento di base dei logaritmi, § 45
proprietà dei logaritmi, § 39
uso dei logaritmi decimali come strumento di calcolo (esempi riepilogativi), § 43
Mantisse dei logaritmi decimali:
dei numeri da 1 a 1.000, tav. 59, § 41
dei numeri da 1.000 a 10.000, tav. 60,
§ 41
11
/
dei numeri da 10.0QO a 11.500, tav.
61, § 44
Moltiplicandi fissi, tav. 3, § 2
Montante di una lira:
dopo n anni [(1
i)n], tav. 8, § 5
dopo m mesi, tav. 6, § 5
dopo n anni ed una frazione d'anno,
§5
Montante di una rendita:
posticipata di durata n anni ( 6nii),
tav. 17, § 15
anticipata di durata n anni (3nii), da
tav.17, §15
frazionata (a rate semestrali, trimestrali, ecc., posticipate): da tav. 17 e
23, a; § 19
frazionata (a rate semestrali, trimestrali, ecc., anticipate): da tav. 17 e
23, b; § 19
poliennale, § 20
Morti fra l'età x e l'età (x
1) (ossia d,),
§ 27, tav. 40, ecc.
+
+
Nuda proprietà, § 31, tav. 44
Numeri primi, tav. 49
Pagamenti rateali (tasso effettivo), § 60
Piani di ammortamento di un debito:
a rata costante annuale, tav. 27, § 23
a rata costante semestrale, trimestrale, ecc., § 24
Potenze dei numeri interi:
seconde (o quadrati), tav. 47
terze (o cubi), tav. 47
quarte, quinte e seste, tav. 48
Potenze del numero e, tav. 67, § 51
Premio annuo vitalizio per assicurare una
lira:
alla fine dell'anno nel quale avverrà la
morte (Px), § 28, tav. 43, ecc.
all'atto della morte, in qualunque momento accada (Px), § 2B, tav. 43, ecc.
Premio unico puro per assicurare una lira:
alla fine dell'anno nel quale avverrà la
morte (Ax), § 28, tav. 43, ecc.
all'atto della morte, in qualunque momento accada (Az), § 28, tav. 43, ecc.
Premio unico puro per assicurare una
rendita vitalizia di una lira all'anno:
posticipata (ax), § 28, tav. 43, ecc.
anticipata (iix), § 28, da tav.- 43, ecc.
Probabilità (curva normale standard): ved.
Curva normale standard di probabilità
12
ti
Probabilità di morte (probabilità, per un
individuo di età x, di morire entro
l'anno seguente) (qx), § 27, tav. 40, ecc.
Probabilità di vita (probabilità, per un
individuo di età x, di essere in vita
dopo 1 anno) (px), § 27, tav. 40, ecc.
Procedimento per tentativi, § 54
Quadrati dei numeri interi, tav. 4 7
Radiante, tav. 64
Radici quadrate e cubiche dei numeri
interi, tav. 47
Rata di ammortamento di un debito:
rata annua posticipata ( ocnii), tav. 19,
§ 17
rata annua anticipata (<Xnii), tav. 20,
§ 17
rata semestrale posticipata (per le durate 5, 10, 15, 20, 25 e 30 anni),
tav. 26, § 22
rata semestrale, trimestrale, ecc. posticipata: da tav. 19 e 25, a; § 21, punto a); §§ 57 e 58
rata semestrale, trimestrale, ecc. anticipata: da tav. 19 e 25, b; § 21, punto b)
Rata di costituzione di un capitale:
rata annua posticipata (ermi)• tav. 21,
§ 18
rata annua anticipata (omi), tav. 22,
§ 18
rata semestrale, trime~trale, ecc. posticipata: da tav. 21 e 25, a;§ 21, punto c)
rata semestrale, trimestrale, ecc. ·anticipata: da tav. 21e25, b; § 21, punto d)
Rateazioni di pagamento (tasso effettivo),
§ 60
Reciproci dei numeri interi, tav. 47
Rendita:
posticipata, § 14
anticipata, § 14
immediata, § 14
differita, § 14
frazionata (a rate semestrali, ecc.),
§ 19
poliennale, § 20
tavole: ved. Montante di una rendita e
Valore attuale di una rendita
Scarto quadratico medio, § 50
Scomposizione in fattori primi, tav. 50 e
51, § 36
Sconto:
semplice commerciale, tav. 1 e 2, § l
composto, § 4
razionale, tav. 4, § 3
Simboli di .commutazione (Dx• Nx• Sx•
Cx• Mx• Rx)• § 28, tav. 43, ecc.
Sopravviventi all'età x. (ossia lx)• § 27,
tav. 40, ecc.
Tartaglia (triangolo di), tav. 64, § 49
Tassi equivalenti:
equivalenze fra tassi posticipati:
a) valori di ik, dato i: tav. 11, § 10
b) valori di jk, dato i: tav. 12, § 10
c) valori di i, dato h: tav. 13, § 10
equivalenze fra tassi anticipati e tassi
posticipati, e viceversa:
d) valori di i, dato ia (interesse semplice): tav. 14, § 11
e) valori di ia• dato i (interesse semplice): tav. 15, § 12
f) valori di i, dato ia (interesse composto): tav. 16, § 13
Tasso istantaneo di mortalità (µx), § 27,
tav. 40, ecc.
Tasso nominale convertibile k volte nell'anno (ossia convertibile semestralmente, trimestralmente, ecc.), § 10
Tempo intercorrente fra due date, § 48,
tav. 62 e 63
Tentativi (procedimento per), § 54
Trasformazione di logaritmi:
decimali in neperiani, § 47, tav. 57
neperiani in decimali, § 47, tav. 57
Triangolo di Tartaglia, tav. 64, § 49
/
Unità di misura:
del sistema inglese: tav. 68, a; § 52
del sistema USA: tav. 68, b; § 52
agrarie locali italiane: 'tav. 68, c; § 52
Usufrutto vitalizio, § 31, tav. 44
Valore attuale di una lira esigibile:
dopo n anni ('Vn), tav. 9, § 7
dopo m mesi, tav. 7, § 7
dopo g giorni (sconto razionale), tav.
4, § 3
dopo n anni ed una frazione d'anno,§ 7
Valore attuale di una rendita:
posticipata di durata n anni (ami)• tav.
18, § 16
anticipata di durata n anni (iim;). da
tav. 18, § 16
frazionata (a rate semestrali, trimestrali, ecc., posticipate): da tav. 18 e
23, a; § 19
frazionata (a rate semestrali, trimestrali, ecc., anticipate): da tav. 18 e
23, b; § 19
perpetua, § 16
poliennale, § 20
vitalizia posticipata (ax): tav. 43, ecc.,
§ 28; tav. 45 e 46, § 32
vitalizia anticipata ( iix): da tav. 43,
ecc., § 28; da tav. 45 e 46, §§ 32 e 28
Valore :finale: ved. Montante
Valore iniziale: ved. Valore attuale
Valore scontato: ved. Valore attuale
Vita media di un individuo di età x (ossia
~x), § 27, tav. 40, ecc.
Vita probabile di un individuo di età x
(ossia "x)• § 27, tav. 40, ecc.
13
luigi brasca
m. marchi / a. fa cchinetti
I c. bra sca
TAVOLE MATEMATICHE
ad uso del le facoltà universitari e
2a edizione
Un testo che rappresenta lo sviluppo, a livello universitario, dei notissimi
testi del prof. Brasca.
Una efficace ed organica sintesi di nozioni fondamentali, riguardanti tutti
i principali argomenti della matematica.
Un'ampia raccolta di schemi riassuntivi.
Un importante strumento ausiliario per la preparazione degli esami di matemat ica generale e di statistica.
Oltre 1.000 integrali calcolati, con l'indicazione della traccia completa di
calcolo.
Un testo assimilabile ad un dizionario della matematica (l'indice analitico
comprende circa 1.000 voci) .
Un prezzo eccezionalmente basso.
INDICE DEL VOLUME
Parte I.
Cap.
»
•
•,.
)I
»
»
»
))
1
2
3
4
5
6
7
8
9
10
Richiami di teoria (539 pagine)
Algebra astratta
pag.
3
Algebra elementare
» 11
)I
Calcolo vettoriale
19
)I
Derivate
29
)I
Equu1oni differenziali
33
Funzioni esponenziali
)I
e iperboliche
67
Funzioni speciali
» 75
Geometria analitica
» 85
))
Geometria elementare
107
Integrali - Nozioni fonda))
mentali
117
Cap. 11
» 12
)I
13
» 14
» 15
)I
16
» 17
))
))
))
18
19
20
Integrali indefiniti calcolati pag.
)I
Integrali definiti calcolati
)I
Matrici, determinanti, ecc.
)I
Momenti di inerzia
)I
Numeri complessi
Studio dell'andamento delle
»
funzioni
Successioni e serie
»
Trasformata di laplace
»
))
Trasformate di Fourier
Trigonometria
»
149
461
473
483
487
491
497
515
521
527
Parte Il. Guida alla r iaoluzlone d i problemi (89 pagg.) (matematica finanziaria e calcoli di
convenienza economica; sistemi di numerazione a base 2, 8 e 16; statistica e calcolo
delle probabilità; ecc.)
Parte 111. Tavole (341 pagg.) (sono riportate, oltre alle tavole di uso più ricorrente, numerose altre
tavole, quali le tavole riguardanti le funzioni esponenziali e iperboliche, le funzioni
speciali, la statistica ed il calcolo delle probabilità, ecc.: in complesso 83 tavole)
L. 12. 5 0 0
/
.
'~
.,