Riepilogo dei moduli

LICEO SCIENTIFICO “L. DA VINCI” - ANNO SCOLASTICO 2013/2014
PROGRAMMA DI FISICA
Svolto nella classe 2^ sezione L
Riepilogo dei moduli
Num.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Titolo
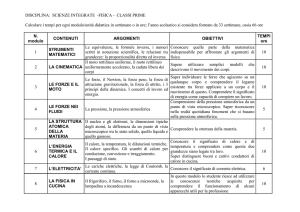
Strumenti matematici
La velocità
L’accelerazione
I moti nel piano
I principi della dinamica
Le forze e il movimento
L’energia e la quantità di moto
La temperatura
Il calore
Tempi
settembre
ottobre
novembre
novembre - dicembre
gennaio
febbraio
febbraio - marzo
marzo - aprile
aprile-maggio
Modulo 1: Strumenti matematici
Prerequisiti
Calcolo aritmetico e algebrico.
Competenze
• Utilizzare le funzioni goniometriche per risolvere triangoli rettangoli.
• Utilizzare correttamente il linguaggio specifico ed il simbolismo per scopi
comunicativi ed operativi.
• Utilizzare le tecniche e le procedure del calcolo aritmetico ed algebrico,
rappresentandole anche sotto forma grafica. Individuare le strategie
appropriate per la soluzione di problemi.
Abilità
• Trasformare gli angoli da gradi a radianti e viceversa.
• Saper usare la calcolatrice per il calcolo delle funzioni goniometriche.
• Saper risolvere triangoli rettangoli.
Conoscenze
• Definizione di radiante. Misura in radianti di angoli notevoli.
1
• Introduzione alle funzioni goniometriche seno,coseno,tangente.
• La risoluzione di triangoli rettangoli mediante le funzioni goniometriche.
Modulo 2: La velocità
Prerequisiti
Strumenti matematici. Unità di misura.
Competenze
• Descrivere la posizione e lo spostamento dei corpi in adeguati sistemi di
riferimento.
• Analizzare e classificare il moto dei corpi.
Tracciare ed interpretare il grafico spazio – tempo.
Abilità
• Riconoscere il sistema di riferimento associato ad un moto.
• Calcolare la velocità media, lo spazio percorso, l’intervallo di tempo in un
moto. Interpretare il coefficiente angolare nel grafico spazio-tempo.
• Conoscere le caratteristiche del moto rettilineo uniforme.
Conoscenze
• Il punto materiale in movimento. I sistemi di riferimento.
• Il moto rettilineo. La velocità media.
• Calcolo della distanza e del tempo. Il grafico spazio-tempo.
• Il moto rettilineo uniforme.
• Calcolo della posizione e del tempo nel moto uniforme.
Modulo 3: L’accelerazione
Prerequisiti
Modulo precedente.
Competenze
• Analizzare e classificare il moto dei corpi ricorrendo alle grandezze velocità
ed accelerazione.
2
• Tracciare ed interpretare i grafici spazio-tempo e velocità-tempo.
Abilità
• Calcolare la velocità istantanea e l’accelerazione media.
• Calcolare l’accelerazione da un grafico velocità-tempo.
• Ricavare lo spazio percorso da un grafico velocità-tempo.
Conoscenze
• I concetti di velocità istantanea, di accelerazione media ed istantanea.
• Le caratteristiche del moto uniformemente accelerato.
• Le leggi del moto.
• I grafici spazio-tempo e velocità-tempo.
Modulo 4: I moti nel piano
Prerequisiti
Strumenti matematici. Unità di misura. Grafici cartesiani.
Competenze
• Riconoscere questioni che possono essere indagate in modo scientifico.
• Applicare conoscenze scientifiche in una data situazione.
• Schematizzare situazioni reali selezionando i parametri significativi.
• Formulare ipotesi, sperimentare e/o interpretare leggi fisiche, proporre e
utilizzare modelli e analogie.
Abilità
• Applicare le conoscenze sulle grandezze vettoriali ai moti nel piano.
• Operare con le grandezze fisiche scalari e vettoriali. Calcolare le grandezze
caratteristiche del moto circolare uniforme.
• Risolvere semplici problemi sul moto circolare uniforme.
Conoscenze
• I vettori posizione, spostamento e velocità.
• Il moto circolare uniforme.
• Periodo, frequenza e velocità istantanea nel moto circolare uniforme.
L’accelerazione centripeta.
• Approfondimenti: il moto armonico.
3
Modulo 5: I principi della dinamica
Prerequisiti
Strumenti matematici. Unità di misura. Grafici cartesiani. Moduli precedenti.
Competenze
• Saper riconoscere i vari tipi di forze che sono coinvolti in semplici contesti
fenomenologici.
• Saper formalizzare e risolvere semplici problemi che coinvolgono varie
forze, utilizzando i principi della dinamica.
• Saper esprimere il concetto di forza come interazione fra corpi.
Abilità
• Analizzare il moto dei corpi quando la forza risultante applicata è nulla.
Riconoscere i sistemi di riferimento inerziali.
• Studiare il moto di un corpo sotto l’azione di una forza costante.
• Applicare il terzo principio della dinamica.
• Proporre esempi di applicazione della legge di Newton.
Conoscenze
• I principi della dinamica. L’enunciato del primo principio della dinamica.
• I sistemi di riferimento inerziali.
• Il principio di relatività galileiana. Il secondo principio della dinamica.
• Unità di misura delle forze nel SI.
• Il concetto di massa inerziale. Il terzo principio della dinamica.
Modulo 6: Le forze e il movimento
Prerequisiti
Strumenti matematici. Unità di misura. Grafici cartesiani. Moduli precedenti.
Competenze
• Schematizzare situazioni reali selezionando i parametri significativi.
• Formulare ipotesi, sperimentare e/o interpretare leggi fisiche, proporre e
utilizzare modelli e analogie.
Abilità
• Analizzare il moto di caduta dei corpi.
4
• Distinguere tra peso e massa di un corpo.
• Studiare il moto dei corpi lungo un piano inclinato.
• Analizzare il moto dei proiettili con velocità iniziali diverse. Risolvere
semplici problemi.
• Comprendere le caratteristiche del moto armonico e del moto del pendolo.
Conoscenze
• Il moto di caduta libera dei corpi.
• La differenza tra i concetti di peso e di massa.
• Il moto lungo un piano inclinato.
• La forza centripeta.
• Approfondimenti: le caratteristiche del moto dei proiettili. Il moto
armonico e il pendolo.
Modulo 7: L’energia
Prerequisiti
Strumenti matematici. Unità di misura. Moduli precedenti.
Competenze
• Schematizzare situazioni reali selezionando i parametri significativi.
• Formulare ipotesi, sperimentare e/o interpretare leggi fisiche, proporre e
utilizzare modelli e analogie.
• Risolvere semplici problemi.
Abilità
• Calcolare il lavoro compiuto da una forza.
• Calcolare la potenza.
• Ricavare l’energia cinetica di un corpo, anche in relazione al lavoro svolto.
Calcolare l’energia potenziale gravitazionale di un corpo e l’energia
potenziale elastica di un sistema oscillante. Applicare il principio di
conservazione dell’energia meccanica.
Conoscenze
• La definizione di lavoro.
• La potenza. Il concetto di energia.
• L’energia cinetica e la relazione tra lavoro ed energia cinetica.
• L’energia potenziale gravitazionale e l’energia elastica.
5
• Il principio di conservazione dell’energia meccanica.
• La conservazione dell’energia totale.
Modulo 8: La temperatura
Prerequisiti
Strumenti matematici. Moduli precedenti.
Competenze
• Applicare il fenomeno della dilatazione termica.
• Applicare le leggi di Boyle .
Abilità
• Comprendere la differenza tra un termometro ed un termoscopio.
• Calcolare la dilatazione dei corpi solidi e liquidi sottoposti a riscaldamento.
Riconoscere diversi tipi di trasformazione di un gas.
Conoscenze
• Definizione operativa di temperatura.
• Termoscopi e termometri. Scale termometriche.
• La dilatazione termica.
• Le trasformazioni dei gas.
• Legge di Boyle
Attività di laboratorio
Dilatazione termica.
Modulo 9: Il calore
Prerequisiti
Modulo precedente. Lavoro, energia, principi di conservazione dell’energia. Stati
di aggregazione della materia.
Competenze
• Individuare le diverse modalità di trasformazione del calore.
• Calcolare le quantità di calore trasferite durante il riscaldamento di un
corpo o durante un passaggio di stato.
6
Abilità
• Comprendere come riscaldare un corpo con il calore o con il lavoro.
• Distinguere tra capacità termica dei corpi e calore specifico delle sostanze.
Calcolare la temperatura di equilibrio in un calorimetro.
• Distinguere i diversi modi di trasformazione del calore.
Conoscenze
• Calore e lavoro come forme di energia in transito.
• Unità di misura per il calore. Capacità termica, calore specifico. Il
calorimetro. Meccanismi di propagazione del calore.
• Cambiamenti di stato.
Attività di laboratorio
Calorimetro- Temperatura di equilibrio.
Gli alunni
______________________
_______________________
La docente
Prof.ssa Gesualda Laganà
______________________
7
LICEO SCIENTIFICO”L. DA VINCI”ANNO SCOLASTICO 2013/14
PROGRAMMA SVOLTO DI FISICA
CLASSE 3^ SEZIONE L
Riepilogo dei moduli
Num.
Titolo
1
Le grandezze scalari e vettoriali
2
Raccordo primo biennio – secondo biennio.
Moti
3
Principio di composizione dei movimenti
4
Dinamica
5
Moto circolare e moto armonico
6
Lavoro ed energia .
7
La quantità di moto
8
La gravitazione
Modulo 1: Le grandezze scalari e vettoriali
Prerequisiti
• Teorema di Pitagora
Competenze
• Utilizzare le tecniche e le procedure del calcolo aritmetico ed algebrico
Confrontare grandezze scalari e vettoriali.
Abilità
• Distinguere le grandezze scalari da quelle vettoriali.
• Eseguire la somma di vettori con il metodo punto-coda e con il metodo
del parallelogramma.
• Eseguire la sottrazione tra due vettori, la moltiplicazione di un vettore per
un numero, il prodotto scalare e vettoriale di due vettori.
• Saper scomporre un vettore nelle sue componenti cartesiane utilizzando i
versori.
Conoscenze
• Le caratteristiche di un vettore.
1
• La differenza tra grandezze scalari e vettoriali.
• Le operazioni di somma, sottrazione moltiplicazione, la scomposizione e la
proiezione di un vettore.
• Il prodotto scalare e vettoriale.
• L’espressione in coordinate cartesiane dei vettori e delle operazioni sui
vettori.
Attività di laboratorio
Esperienze sui vettori.
Modulo 2: Raccordo primo biennio – secondo biennio. Moti
Prerequisiti
• Le basi dell’algebra dei numeri relativi.
• Le principali proporzionalità tra grandezze.
• Le basi del metodo sperimentale.
• La struttura logica delle teorie scientifiche.
• I vettori. Velocità media e accelerazione media.
• La legge oraria. La tangente di una curva in un punto.
• Il coseno di un angolo. L’angolo al centro.
• La definizione operative di durata, lunghezza e massa con le loro unità di
misura. I sistemi di riferimento.
• Risolvere equazioni di primo grado.
• Utilizzare in modo corretto le unità di misura del S. I.
Competenze
• Interpretare grafici di moto ed effettuare derivazione e integrazione grafica.
Utilizzare le leggi dei moti.
• Analizzare fenomeni fisica e applicazioni tecnologiche, riuscendo a
individuare le grandezze fisiche caratterizzanti e a proporre relazioni
quantitative tra esse.
Abilità
• Esser in grado di descrivere i fenomeni osservati con un linguaggio
appropriato. Saper rappresentare in grafici (spazio -tempo), (velocità tempo) i diversi tipi di moto osservati.
• Saper interpretare grafici. Saper dedurre da grafici i diversi tipi di moto
osservati. Saper enunciare le leggi relative a spostamento, velocità e tempo
quando l’accelerazione è costante.
• Saper individuare le grandezze fisiche necessarie per la descrizione del
fenomeno osservato.
• Saper risolvere semplici problemi utilizzando un linguaggio algebrico e
grafico appropriato.
2
Conoscenze
• Concetti fondamentali per la descrizione del moto: punto materiale,
traiettoria, legge oraria.
• Il moto rettilineo uniforme; grafici.
• Il moto vario; velocità media e istantanea, accelerazione media e istantanea;
grafici.
• Il moto rettilineo uniformemente vario: la dipendenza velocità-tempo,
spazio- tempo, velocità-spazio; grafici.
• Moti uniformemente accelerati: moto di caduta di un grave; moto di caduta
di un corpo su un piano inclinato.
Attività di laboratorio
Moto rettilineo uniforme e uniformemente accelerato su rotaia.
Modulo 3: Principio di composizione dei movimenti
Prerequisiti
• Le basi dell’algebra dei numeri relativi.
• Le principali proporzionalità tra grandezze.
• Le basi del metodo sperimentale.La struttura logica delle teorie
scientifiche.
• I vettori. Velocità media e accelerazione media. La legge oraria.
• La tangente di una curva in un punto. Il coseno di un angolo. L’angolo al
centro. La definizione operative di durata, lunghezza e massa con le loro
unità di misura. I sistemi di riferimento.
• Gli errori sperimentali.
• Risolvere equazioni di primo grado.
• Utilizzare in modo corretto le unità di misura del S. I.
Competenze
• Analizzare fenomeni fisica e applicazioni tecnologiche, riuscendo a
individuare le grandezze fisiche caratterizzanti e a proporre relazioni
quantitative tra esse.
Abilità
• Esser in grado di descrivere i fenomeni osservati con un linguaggio
appropriato. Saper individuare le grandezze fisiche necessarie per la
descrizione del fenomeno osservato.
• Saper risolvere semplici problemi utilizzando un linguaggio algebrico e
grafico appropriato.
3
Conoscenze
• Principio di inerzia.
• Il principio di composizione dei movimenti. Il moto parabolico.
• Trasformazioni galileiane.
Modulo 4: Dinamica
Prerequisiti
• Il moto rettilineo uniforme.
• Il moto rettilineo uniformemente accelerato.
• Il moto circolare uniforme Il moto parabolico.
• Determinare la posizione e calcolare la velocità nei vari tipi di moto.
• La rappresentazione grafica delle grandezze fisiche. I sistemi di
riferimento.
• Utilizzare in modo corretto le unità di misura del S.I.
Competenze
• Formulare ipotesi, sperimentare e/o interpretare leggi fisiche, proporre e
utilizzare modelli e analogie.
• Analizzare fenomeni fisici e applicazioni tecnologiche, riuscendo a
individuare
• le grandezze fisiche caratterizzanti e a proporre relazioni quantitative tra
esse. Risolvere problemi utilizzando il linguaggio algebrico e grafico,
nonché il Sistema Internazionale delle unità di misura.
• Abilità
• Essere in grado di definire i concetti di forza e di massa e di enunciare i
principi della dinamica.
• Essere in grado di proporre esempi di sistemi inerziali e non inerziali e
riconoscere le forze apparenti e quelle attribuibili a interazioni.
• Essere in grado di applicare le proprietà vettoriali delle grandezze fisiche
incontrate allo studio dei fenomeni esaminati e risolvere esercizi e
problemi.
• Essere in grado di proporre esempi di sistemi inerziali e non inerziali e
riconoscere le forze apparenti e quelle attribuibili a interazioni.
4
Conoscenze
• La prima legge della dinamica.
• La seconda legge: la relazione fra forza e accelerazione.
• Massa e peso di un corpo.
• Il principio di azione e reazione.
• La seconda legge della dinamica e la forze di attrito.
• Applicazioni della seconda legge della dinamica.
• Leggi della dinamica e sistemi di riferimento.
Attività di laboratorio
Verifica dei principi della dinamica su rotaia. Piano inclinato (liscio e scabro).
Modulo 5: Moto circolare e moto armonico
Prerequisiti
• Il moto rettilineo uniforme.
• Il moto rettilineo uniformemente accelerato.
• Il moto circolare uniforme.
• Determinare la posizione e calcolare la velocità nei vari tipi di moto.
• La rapprsentazione grafica delle grandezze fisiche. I sistemi di riferimento.
• Utilizzare in modo corretto le unità di misura del S.I.
Competenze
• Formulare ipotesi, sperimentare e/o interpretare leggi fisiche, proporre e
utilizzare modelli e analogie.
• Analizzare fenomeni fisici e applicazioni tecnologiche, riuscendo a
individuare le grandezze fisiche caratterizzanti e a proporre relazioni
quantitative tra esse. Risolvere problemi utilizzando il linguaggio algebrico
e grafico, nonché il SI delle unità di misura.
Abilità
• Distinguere la forza centripeta e centrifuga apparente.
• Comprendere le caratteristiche del moto armonico e del moto del pendolo.
Conoscenze
• I moti curvilinei, velocità e accelerazioni.
• Il moto circolare uniforme: la cinematica e la dinamica.
• Cinematica del moto uniformemente accelerato.
• Dinamica del moto uniformemente accelerato.
5
• Moto armonico. Velocità ed accelerazione nel moto armonico.
• Dinamica del moto armonico: la forza elastica.
• Pendolo semplice.
Modulo 6: Lavoro ed energia
Prerequisiti
• I diversi tipi di moto.
• Le forze. Scomposizione delle forze.
• Il momento di una forza e le condizioni di equilibrio.
• Le leggi della dinamica e le loro applicazioni.
• La rappresentazione vettoriale delle grandezze fisiche.
• I sistemi di riferimento.
• Utilizzare in modo corretto le unità del S.I.
Competenze
• Calcolare il lavoro svolto o la potenza erogata.
• Distinguere tra forze conservative e non conservative.
• Applicare il teorema dell’energia cinetica a situazioni semplici.
• Descrivere trasformazioni di energia da una forma a un’altra.
• Applicare il principio di conservazione dell’energia meccanica.
Abilità
• Calcolare il lavoro fatto da una forza costante nei diversi casi di angolo tra
direzione della forza e direzione dello spostamento.
• Calcolare la potenza impiegata.
• Ricavare l’energia cinetica di un corpo in relazione al lavoro svolto.
• Determinare il lavoro svolto da forze dissipative.
Conoscenze
• Lavoro. Potenza. Forze conservative e non conservative.
• Energia potenziale ed energia conetica.
• Pendolo elastico. La conservazione dell’energia meccanica in un pendolo.
6
Modulo 7: La quantità di moto e il momento angolare
Prerequisiti
• Lavoro ed energia cinetica.
• L’energia potenziale. L’attrito.
• Moto circolare uniforme. Moto rotatorio.
Competenze
• Distinguere tra forze conservative e non conservative.
• Utilizzare nell’analisi di un sistema fisico la conservazione della quantità di
moto totale e del momento angolare totale.
Abilità
• Calcolare la quantità di moto di un corpo e l’impulso di una forza.
• Applicare la legge di conservazione della quantità di moto.
• Comprendere la distinzione tra urti elastici e anelastici.
• Analizzare casi di urti lungo una retta di urti obliqui.
• Individuare la posizione del centro di massa di un sistema fisico.
Conoscenze
• La relazione tra quantità di moto e impulso di una forza.
• La legge di conservazione della quantità di moto per un sistema isolato.
• Urti elastici e anelastici su una retta e nel piano.
• Il centro di massa e le sue proprietà.
Modulo 8: La gravitazione
Prerequisiti
• Equazioni del moto circolare uniforme.
• Forza centripeta e moto circolare.
• Principi della dinamica.
• Moto parabolico.
• Principi di conservazione.
• Definizione di ellisse.
Competenze
• Formulare ipotesi, sperimentare e/o interpretare leggi fisiche, proporre e
utilizzare modelli e analogie.
• Analizzare fenomeni fisici, riuscendo a individuare
7
le grandezze fisiche caratterizzanti e a proporre relazioni quantitative tra
esse.
• Risolvere problemi utilizzando il linguaggio algebrico e grafico, nonché il
SI delle unità di misura.
Abilità
• Applicare i principi della dinamica e la legge di gravitazione universale allo
studio del moto dei pianeti e dei satelliti nel caso di orbite circolari.
• Applicare il principio di conservazione dell’energia.
Conoscenze
• Modelli geocentrici ed eliocentrici.
• La rivoluzione copernicana. Tycho Brahe. Le leggi di Keplero.
• La legge di gravitazione universale.
• Applicazioni della legge di gravitazione universale.
• Il campo gravitazionale.
• Energia potenziale gravitazionale.
Gli alunni
___________________________
___________________________
La docente
Prof.ssa Gesualda Laganà
________________________
8
9
LICEO SCIENTIFICO”L. DA VINCI”ANNO SCOLASTICO 2013/14
PROGRAMMA SVOLTO DI MATEMATICA
CLASSE 3^ SEZIONE L
Riepilogo dei moduli
Num.
1
Titolo
Richiami di geometria euclidea
2
Insiemi numerici e strutture
3
Il metodo delle coordinate
4
Relazioni e funzioni – Trigonometria
5
Geometria analitica
Modulo 1: Richiami di geometria euclidea
Prerequisiti
Geometria euclidea relativa alle proprietà dei triangoli e della circonferenza
Conoscenze
UDA 1
•
•
•
•
•
Teoremi di Euclide- applicazione della similitudine
Lunghezza della circonferenza e area del cerchio.
Lunghezza di un arco.
Area di un settore circolare e di un segmento circolare.
Raggio del cerchio inscritto e circoscritto ad un triangolo.
Modulo 2: Insiemi numerici e strutture
Prerequisiti
Disequazioni di primo grado
Competenze disciplinari
Acquisire la tecnica di risoluzione delle disequazioni per l’applicazione in vari campi degli
studi successivi
1
Abilità
Saper risolvere equazioni e disequazioni.
Conoscenze
UDA 1
UDA 2
EQUAZIONI
• Equazioni lineari, di secondo grado, di grado superiore al II,
• fratte. Equazioni irrazionali ed in valore assoluto.
DISEQUAZIONI
• Disequazioni lineari, di secondo grado, di grado superiore al II,
fratte.
• Disequazioni irrazionali ed in valore assoluto.
• Sistemi di disequazioni
Modulo 3: Il metodo delle coordinate
Prerequisiti
Teorema di Pitagora, punto medio di un segmento, teorema di Talete.
Competenze disciplinari
Introdurre lo studio della geometria analitica formalizzando le conoscenze elementari.
Abilità
Saper definire la misura di un segmento orientato. Saper determinare la distanza tra due
punti,., il punto medio di un segmento, il baricentro di un triangolo. Saper scrivere le
equazioni di una simmetria centrale. Saper determinare e utilizzare le formule della
traslazione degli assi.
Conoscenze
UDA 1
IL METODO DELLE COORDINATE
• Segmenti orientati e loro misura. Ascisse sulla retta.
• Coordinate cartesiane ortogonali nel piano.
• Distanza di due punti.
• Coordinate del punto di mezzo di un segmento.
• Coordinate del baricentro di un triangolo.
• Area di un triangolo. Traslazione.
Modulo 4: Relazioni e funzioni – Trigonometria
Prerequisiti
Teoria degli insiemi - Angolo e misura di un angolo, il radiante, geometria piana
Competenze disciplinari
• Comprendere il concetto di relazione binaria, definirne e saperne riconoscere le
proprietà. Definire il concetto di funzione
• Convertire un’ampiezza in gradi in una in radianti e viceversa; definire le funzioni
goniometriche con le loro proprietà, stabilire le relazioni fondamentali fra le funzioni,
2
risolvere problemi che coinvolgono triangoli rettangoli .
Abilità
• Saper operare con le funzioni
• Saper definire le funzioni goniometriche. Saper rappresentare graficamente le funzioni
goniometriche. Saper determinare le funzioni goniometriche di angoli particolari. Saper
ricavare le relazioni che legano tra loro gli archi associati. Saper risolvere espressioni
applicando le formule studiate.
Conoscenze
UDA 1
RELAZIONI E FUNZIONI
• Relazioni binarie.
• Funzioni. Funzioni iniettive, suriettive e biettive.
UDA 2
FUNZIONI GONIOMETRICHE
• Sistema cartesiano ortogonale associato ad un angolo orientato.
Seno , coseno , tangente , cotangente , secante e cosecante di un
angolo orientato e loro proprietà.
• Funzioni goniometriche di alcuni angoli notevoli.
• Espressione di tutte le funzioni goniometriche di un dato angolo
orientato mediante una sola di esse.
• Angoli associati.
• Riduzione al primo quadrante.
• Formule di addizione, sottrazione, duplicazione, bisezione,
prostaferesi
Modulo 5: Geometria analitica
Prerequisiti
Il teorema di Talete, abilità di calcolo algebrico (equazioni e sistemi).Sistema cartesiano.
Richiami di geometria euclidea sulle trasformazioni geometriche piane. Le proprietà
geometriche della circonferenza, i sistemi algebrici di II grado e di grado superiore al
secondo. Elementi fondamentali del piano cartesiano e della funzione lineare. Calcolo
algebrico
Competenze disciplinari
• Determinare l’equazione cartesiana della retta. Acquisire il significato del coefficiente
angolare della retta. Studiare il parallelismo e la perpendicolarità, distanza di un punto da
una retta ,angolo di due rette, equazioni di assi, bisettrici, mediane e altezze di un
triangolo, fasci di rette.
• la circonferenza come luogo geometrico, determinarne l’equazione canonica,
evidenziarne le proprietà.
• Definire la parabola come luogo geometrico di punti.
•
Abilità
• Saper scrivere l’equazione di una retta. Saper determinare il coefficiente angolare di una
retta. Saper determinare il punto di intersezione di rette incidenti. Saper studiare fasci di
rette. Saper risolvere problemi sulla retta
• Saper definire dal punto di vista geometrico le principali isometrie (simmetrie,
traslazioni e rotazioni) e le similitudini; saper determinare le equazioni analitiche di tali
3
trasformazioni e saperne ritrovare, per via analitica, le più importanti proprietà
• Saper definire la circonferenza come luogo geometrico, saper determinare l’equazione
canonica. Saper riconoscere le posizioni di una retta rispetto ad una circonferenza. Saper
risolvere problemi relativi alla circonferenza ed ai fasci di circonferenze.
• Saper riconoscere l’equazione di una parabola. Saper scrivere l’equazione di una
parabola. Saper riconoscere parabole in posizioni particolari. Saper riconoscere le
posizioni reciproche di una retta e una parabola. Saper scrivere le equazioni di una/delle
retta/e tangente/i ad una parabola. Saper risolvere problemi relativi.
Conoscenze
UDA 1
UDA 2
UDA 4
LA FUNZIONE LINEARE
• Corrispondenza biunivoca fra retta ed equazione lineare in due
variabili
• Forma implicita, esplicita e segmentaria di una retta
Rappresentazione grafica di una retta ; coefficiente angolare
• Casi particolari dell’equazione di una retta
• Condizione di parallelismo e perpendicolarità
• Intersezione fra due rette
• Distanza di un punto da una retta
• Asse di un segmento
• Bisettrice di un angolo ; angolo fra due rette
• Fasci di rette propri e impropri – applicazioni
CIRCONFERENZA E FASCI DI CIRCONFERENZE
• L’equazione cartesiana della circonferenza.
• Circonferenza con particolari valori di coefficienti.
• Questioni elementari sulla circonferenza.
• Posizioni di rette e circonferenza; problema delle tangenti.
• Fascio di circonferenze: circonferenze per due punti; circonferenze
tangenti ad un retta in un punto; circonferenze concentriche.
Problemi relativi.
• Grafici di curve di data equazione.
PARABOLA E FASCI DI PARABOLE
• Conoscere la definizione di parabola .
• Equazione cartesiana.
• Mutue posizioni di una retta ed una parabola.
Gli alunni
__________________________
___________________________
La docente
Prof.ssa Gesualda Laganà
______________________
4
LICEO SCIENTIFICO”L. DA VINCI”ANNO SCOLASTICO 2013/14
PROGRAMMA SVOLTO DI MATEMATICA
CLASSE 4^ SEZIONE L
Riepilogo dei moduli
Num.
Titolo
1
2
3
4
Approfondimenti di geometria analitica
Trigonometria
Funzione esponenziale e logaritmica
Complementi di algebra
5
Geometria dello spazio
6
Calcolo combinatorio
Modulo 1: Approfondimenti di geometria analitica
Conoscenze
•
U.A.
Luoghi
geometrici
Contenuti
Principali luoghi geometrici
Modulo 2: Goniometria e Trigonometria
Competenze
• identità ed equazioni goniometriche
di vario tipo
• disequazioni goniometriche di vario
tipo
• principali formule di applicazione
della trigonometria alla geometria
Abilità
• applicare le principali formule
goniometriche per dimostrare
identità, risolvere equazioni e
disequazioni, risolvere problemi di
geometria
Conoscenze
U.A.
Contenuti
Addizione. Sottrazione. Duplicazione. Bisezione. Prostaferesi.
• formule di
trasformazione Werner. Formule parametriche.
1
•
Identità –
Identità goniometriche – equazioni goniometriche elementari,
Equazioni
lineari in senx e cosx, omogenee di II grado, biquadratiche
goniometriche omogenee, simmetriche
•
Disequazioni Disequazioni goniometriche elementari o riconducibili ad
goniometriche esse, lineari in senx e cosx, di II grado omogenee.
•
Applicazioni
Risoluzione dei triangoli – area di un triangolo – area di un
parallelogrammo – raggio delle circonferenze inscritta,
circoscritta ed exinscritta in un triangolo – area di un
quadrilatero
Modulo 3: Funzione esponenziale e logaritmica
•
•
•
•
•
•
Competenze
concetto di potenza
proprietà delle potenze
grafico della funzione esponenziale
concetto di logaritmo
proprietà dei logaritmi
grafico della funzione logaritmica
Abilità
• risolvere equazioni e disequazioni
esponenziali
• risolvere equazioni e disequazioni
logaritmiche
• costruire il grafico di funzioni
esponenziali e logaritmiche
Conoscenze
U.A.
Funzione
esponenziale
Contenuti
Potenza con esponente reale di un numero reale positivo –
funzione esponenziale – grafico delle funzioni esponenziali
•
Funzione
logaritmica
Concetto di logaritmo – proprietà dei logaritmi – funzione
logaritmica e suo grafico – passaggio da un sistema di
logaritmi ad un altro – logaritmi decimali
•
Equazioni e
Equazioni esponenziali – equazioni logaritmiche – equazioni
disequazioni risolte graficamente – disequazioni esponenziali – disequazioni
logaritmiche e logaritmiche –
esponenziali
•
Modulo 4: Complementi di algebra
Competenze
• concetto di numero complesso
• rappresentazioni geometriche dei
numeri complessi
Abilità
• eseguire operazioni sui numeri
complessi
• rappresentare geometricamente e
2
• forma trigonometrica dei numeri
complessi
• teorema fondamentale dell’Algebra
• definizione di progressione
aritmetica e geometrica e relative
formule
• definizione di sistema di coordinate
polari
•
•
•
•
•
trigonometricamente i numeri
complessi
eseguire operazioni sui numeri
complessi scritti in forma
trigonometrica
risolvere equazioni di secondo grado
nel campo complesso
riconoscere successioni e
progressioni
applicare le formule delle
progressioni aritmetiche e
geometriche
utilizzare il sistema di coordinate
polari
Conoscenze
•
•
U.A.
Contenuti
Numeri
Definizione di numero complesso – operazioni sui numeri
complessi complessi – il campo complesso come ampliamento del campo
reale – rappresentazioni geometriche dei numeri complessi –
piano di Gauss – coordinate polari- coordinate polari ed equazioni
delle curve- forma trigonometrica dei numeri complessi –
prodotto e quoziente di due numeri complessi scritti in forma
trigonometrica – potenza con esponente intero di un numero
complesso – equazioni di secondo grado nel campo complesso –
Progressio Definizione di successione –progressioni aritmetiche – calcolo del
ni
termine an di una progressione aritmetica – somma di termini
consecutivi – progressioni geometriche – calcolo del termine an di
una progressione geometrica – prodotto e somma di termini
consecutivi
Modulo 5: Geometria dello spazio
Competenze
• posizioni reciproche di rette e piani
nello spazio
• diedri e piani perpendicolari
• angoloide, prisma, parallelepipedo,
Abilità
• riconoscere le posizioni reciproche
di rette e piani nello spazio
• calcolare superfici e volumi dei solidi
3
piramide, tronco di piramide,
poliedri regolari
• solidi di rotazione
• superfici e volumi dei solidi
Conoscenze
•
•
•
U.D.
Rette e
piani
nello
spazio
Poliedri e
solidi di
rotazione
Contenuti
Assioma di partizione dello spazio – posizioni reciproche di due
rette nello spazio – posizioni reciproche di due piani nello spazio –
posizioni reciproche di una retta e di un piano nello spazio – diedri
e piani perpendicolari
Definizione di angoloide – prisma indefinito – prismi retti e regolari
– parallelepipedo e cubo – piramide – tronco di piramide – poliedri
regolari – cilindro – cono – tronco di cono – superficie sferica –
sfera – parti della superficie sferica e della sfera
Superfici Area della superficie di: prisma retto, parallelepipedo rettangolo,
e volumi cubo, piramide retta, tronco di piramide regolare, cilindro, cono,
dei solidi tronco di cono, sfera e parti della sfera – principio di Cavalieri –
equivalenze notevoli – volume dei solidi studiati
Modulo 6: Calcolo combinatorio
Conoscenze
UA 1
Calcolo
combinatorio
•
•
•
•
•
Fattoriale
disposizioni, permutazionicombinazioni semplici e con ripetizione –
coefficienti binomiali e loro proprietà –
formula del binomio di Newton
Gli alunni __________________________
___________________________
La docente
Prof.ssa Gesualda Laganà
4
5