Fisica dell’Atmosfera
Lezione 1
Gaetano Festa
Atmosfera
• L’atmosfera ha ca 400 Myr, da quando la terra è ricoperta di alberi
Generata da materiale volatile emesso di vulcani
Prodotti eruttivi: 85% H2O, 10 % CO2, Solfuri
La CO2 proviene dai carbonati, l’H2O dagli oceani.
L’ossigeno si è formato per foto-dissociazione dell’acqua. L’azoto non
è stato inglobato nei cristalli e ha stazionato nell’atmosfera, i gas
nobili per decadimento radioattivo.
• Lo spessore totale è l’ 1% del
raggio della Terra
Semplici modelli di Atmosfera
• La temperatura media della superficie terrestre è 288 K
Il flusso medio di potenza per unità di area proveniente dal Sole
(costante solare) è Fs=1370 W/m2.
Flusso incidente parallelo alla Terra, contenuto in un tubo di area
πa2
P = (1 − A) FS π a 2
A Albedo medio : A = 0.3
Terra come corpo Nero
Assumendo che la Terra irradi a temperatura costante T con potenza
per unità di area pari a
I = σT 4
La potenza associata, se l’emissione è isotropa è
P ' = 4π a 2σ T 4
Eguagliando si ha che
2
4
4π a σ T = (1 − A) Fsπ a
2
(1 − A) Fs
T=
= 255 K
4σ
4
Atmosfera a due strati
F0
Ta
Fa
Atmosfera
AsF0
Tg
AtFg
Fa
Fg
Suolo
L’atmosfera trasmette una frazione As della radiazione solare a
piccola lunghezza d’onda (visibile) al suolo e re-emette verso
l’esterno una frazione At a più grande lunghezza d’onda (infra-rosso).
Tenendo conto della differenza fra le superfici di flusso e l’albedo
1
2
F0 = (1 − A) Fs = 240W / m
4
Modello a due strati
Emissione del suolo
Fg = σ Tg4
Emissione dell’atmosfera
4
a
Fa = (1 − At )σ T
Bilanciando i flussi
F0 = Fa + At Fg
Fg = As F0 + Fa
Da cui
1 + As
Fg =
F0
1 + At
Modello a due strati
In un modello di effetto serra si ha che
As = 0.9
At = 0.2
Fg = σ Tg4 ⇒ Tg = 286 K
Analogamente
1 + At As
Fa =
F0
1 + At
Ta = 245 K
Idee sul riscaldamento globale
Variazioni di temperatura per perturbazioni di As, At, A
1
1 + As
1 + As
δ Fg = F0
δ As −
δ At −
δ A
2
1 + At
1
(1
)
+
A
−
A
(
)
1
+
A
(
)
t
t
δ Fg
Fg
=
δ As
1 + As
−
δ At
1 + At
−
δA
(1 − A)
=4
δ Tg
Tg
Una diminuzione nella trasmissione termica
δ At < 0 ⇒= δ Tg > 0
Un aumento dell’albedo
δ A > 0 ⇒= δ Tg < 0
Temperatura e stratificazione
Stratificazione
• Troposfera
• Stratosfera
• Mesosfera
• Termosfera
• Esosfera
Perché la temperatura varia:
• la densità diminuisce
• raffreddamento radiativo del
vapore
• assorbimento dell’O3 e O2
Troposfera
• Il gradiente è 6.5 °K/km.
• La temperatura diminuisce perché l’aria è compressibile, a causa
della diminuzione di densità essa si espande
• Il limite superiore (tropopausa) è indicato da un’inversione di
temperatura: è uno strato termico limite (per la convezione)
• Lo spessore della tropopausa varia tra 8km (poli) e 16 km
(equatore): i gradienti termici sono meridionali
• Alle medie latitudini la tropopausa è interrotta : interazione tra
stratosfera e troposfera (passaggio di vapore acqueo e ozono).,
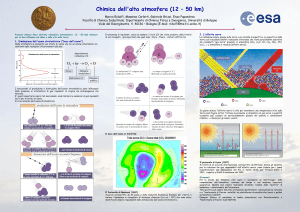
Stratosfera
• Si estende per ca 50 km.
• Ricca di ozono. Variazioni di temperatura sono prodotte
dall’assorbimento differenziale della radiazione con la quota.
• L’assorbimento maggiore è alla stratopausa.
•. Variazioni stagionali : freddi inverni polari possono essere seguiti
da rapide variazioni di temperatura.
• Nella stratosfera equatoriale : venti con ciclicità biennale.
Variazioni zonali di temperatura media
Variazioni zonali di velocità di venti
Composizione dell’Atmosfera
• Atmosfera come una miscela meccanica di gas
•H20 e O3 variano molto rapidamente in spazio e tempo, CO2 cresce
lentamente nel tempo
• N2 e O2, sebbene predominanti, hanno scarsa influenza sulla
dinamica dell’atmosfera, la concentrazione stabile fino a ≈ 100 km
Gas serra
• Assorbono la radiazione ri-emessa dalla terra.
• La loro concentrazione è legata all’attività antropica.
Quali sono ?
CO2 (Anidride carbonica)
O3 (Ozono), distrutto da ossidi di azoto e CFCl
CH4 (Metano)
CH4 + O2 + 2x→ C02 + 2xH2 (x = H, OH, NO…)
N2O (Monossido di azoto)
CFC, HFC (Cloro o Idro – Fluoro – Carburi)
H2O (Acqua)
Ozono
• Prodotto per interazione tra la
radiazione solare (UV) e
l’ossigeno a tra 30 km e 60 km
• L’ozono migra verso i poli
durante i mesi invernali (le notti
polari)
• Ciclo dell’ozono
formazione
O2 + O → O3
distruzione
H + O → H2 O
Cl + O3 → ClO + O2
Buco dell’ Ozono
•Fenomeno Antartico a partire
dagli anni ’70
• Talvolta osservato anche nelle
regioni Artiche
Termodinamica dell’Atmosfera
leggi di stato dei gas perfetti
PV = cost;
(Tcost)
T = costV;
( Pcost)
PV = nrT = NkT
m Nmx mx P
ρ= =
=
V
V
k T
k = 1.381 10−23 J molec −1K −1
−1
r = 8,314 J mol K
−1
m nM x M x P
P
ρ= =
=
=
V
V
r T RxT
Legge dei gas perfetti
Se M è la massa molare dell’aria
r
P = ρ RT = ρ T
M
r = 287 J / ( Kg K )
•La densità varia tra 1.2 kg/m3 (superficie) a 0.7 kg/m3 (5000 m)
•Il 50% della massa dell’atmosfera è contenuta nei primi 5 km
Pressione
Livello medio di pressione dovuto al peso dell’atmosfera:
P = ( Mg 0 ) / (4π a 2 ) = (5.141018 9.81) / (4 3.14 6.3610 6 ) = 1bar
La pressione media è 1013.25 mb
La pressione decresce con la quota. In condizioni di equilibrio
idrostatico si ha
P
dP = −
gdz
dP = − ρ gdz
RT
P
∫
P0
dP '
g
=−
P'
R
z
dz '
∫0 T
Pressione
Nel semplice caso in cui la temperatura è costante
P = P0 e
−
gz
RT
La pressione decresce esponenzialmente. Per un’atmosfera isoterma
a T=260 K, la lunghezza caratteristica
RT
H =
= 7.6 km
g
In un modello a gradiente: T = T0 − Γ z
P
∫
P0
z
T0
dP '
g
dz '
g
=− ∫
=−
log
P'
R 0 T0 − Γ z '
RΓ
T0 − Γ z
T0
P = P0
−
Γ
T
z
0
−
g
RΓ
Entropia
Prima legge della termodinamica
δ U = −δ W + δ Q
Le quantità sono riferite al calore fornito al sistema ed al lavoro fatto
dal sistema.
cvδ T = − pδ V + T δ S = − Rδ T + V δ p + T δ S
c pδ T = V δ p + T δ S
Dividendo per T si ha
δ S = cp
δT
V
δT
δp
− δ p = cp
−R
T
T
T
p
Entropia
Integrando si ha
S = c P log(T ) − R log( p ) + S 0
R 2
−K
S = c P log(Tp ) + S 0 ;
K =
=
cP 7
In un processo adiabatico si ha che
δS = 0
δT
T
=K
δp
p
Da cui
K
p
p0
T
log = log
⇒θ =T
θ
p
p0
K
Temperatura potenziale
p0
θ =T
p
K
θ è la temperatura potenziale di una particella d’aria alla
temperatura T e alla pressione p, definito il valore di riferimento p0=
1000 hPa.
S = c P log(θ ) + S1
Particella d’aria
Consideriamo una particella d’aria in modo tale da poterla
etichettare e seguire la sua posizione e le sue caratteristiche
termodinamiche nel tempo (formalismo lagrangiano). La sua
pressione è la stessa dell’ambiente circostante, ma densità e
temperatura possono essere proprie.
In una trasformazione adiabatica
cp
δT
δp
Rρ g
=R
=
dz
T
p
p
g
dT
=−
= 9.8 K / km
cp
dz δ S = 0
Gradiente adiabatico
z
DALR
v
Effettivo
v
Effettivo
DALR
T
T
Le pressioni sono uguali
Temperatura minore;
Densità maggiore;
Riscende; eq. stabile
Temperatura maggiore;
Densità minore;
Sale; eq. instabile