BSc Federico Guercilena - (INFN)

Corso di laurea triennale in Fisica
STUDIO DI CORRELAZIONE FRA RAGGI COSMICI NELLA
REGIONE DELL’EEV E SORGENTI GALATTICHE CON I DATI
DELL’OSSERVATORIO PIERRE AUGER
Relatore: Dr Lino Miramonti
Correlatore: Dr Viviana Scherini
Elaborato di Federico Guercilena
matricola 709793
Anno Accademico 2009/2010
2
Indice
1 Raggi Cosmici
1.1 Composizione . . . . . . . . . . . . . . .
1.2 Lo Spettro Energetico . . . . . . . . . .
1.3 Origine dei Raggi Cosmici . . . . . . . .
1.3.1 Accelerazione secondo Fermi . . .
1.3.2 Sorgenti Astrofisiche . . . . . . .
1.4 Propagazione dei Raggi Cosmici . . . . .
1.4.1 Effetto dei campi magnetici . . .
1.4.2 L’effetto GZK . . . . . . . . . . .
1.4.3 Propagazione di neutroni e fotoni
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Rivelazione dei raggi cosmici e l’Ossevatorio Pierre Auger
2.1 Fisica degli sciami di particelle atmosferiche . . . . . . . . .
2.1.1 Il modello di Heitler per le cascate elettromagnetiche
2.1.2 Sciami adronici . . . . . . . . . . . . . . . . . . . . .
2.2 Rivelatori di superficie . . . . . . . . . . . . . . . . . . . . .
2.3 Rivelatori di fluorescenza . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
7
8
9
10
11
12
15
15
16
17
.
.
.
.
.
21
22
23
24
25
27
3 Identificazione di eccessi di raggi cosmici nella regione dell’EeV
3.1 Il campione di dati . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Significanza secondo Li-Ma . . . . . . . . . . . . . . . . . . . .
3.3 Generazione del fondo isotropo di riferimento . . . . . . . . . .
3.4 Strategia di scan e ottimizzazione . . . . . . . . . . . . . . . .
3.5 Software e risorse di calcolo . . . . . . . . . . . . . . . . . . .
3.6 Risultati . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 Possibili sorgenti e
4.1 X-Ray Binaries
4.2 Pulsars . . . . .
4.3 Magnetars . . .
studio di
. . . . . .
. . . . . .
. . . . . .
31
32
32
33
34
35
36
correlazione
39
. . . . . . . . . . . . . . . . . . . . 40
. . . . . . . . . . . . . . . . . . . . 41
. . . . . . . . . . . . . . . . . . . . 42
3
4.4
4.5
Supernova Remnants . . . . . . . . . . . . . . . . . . . . . . . 42
Il Centro Galattico . . . . . . . . . . . . . . . . . . . . . . . . 43
5 Conclusioni
47
4
Introduzione
Nonostante siano trascorsi 98 anni dalla scoperta dei raggi cosmici, molte
domande riguardo la loro origine e natura rimangono tuttora senza risposta.
Negli ultimi anni tuttavia è stato effettuato un grande sforzo nel campo della
fisica delle astroparticelle che ha portato ad un notevole miglioramento delle
prestazioni dei rivelatori. Grazie ad i nuovi dati raccolti dagli esperimenti
di ultima generazione si sta ora entrando in una fase nella quale finalmente
sarà possibile cominciare la ricerca di risposte a tali questioni aperte.
In questo panorama occupa una posizione particolare l’Osservatorio Pierre
Auger (Pierre Auger Observatory, PAO). Il progetto dell’Osservatorio sfrutta le più avanzate tecniche di rivelazione, combinando inoltre in un unico
esperimento dispositivi di rivelazione di superficie e di fluorescenza; impiega
due siti di ossevazione, l’uno completo nell’emisfero australe ed un secondo
nell’emisfero boreale (la cui realizzazione è purtroppo compromessa a causa
della mancanza di fondi), ottenendo quindi una completa copertura del cielo
e la massima esposizione totale finora raggiunta; beneficia infine di una collaborazione internazionale di circa 300 scienziati provenienti da 17 nazioni.
I dati raccolti dall’Osservatorio permettono ora studi che hanno come scopo
di rispondere alle domande sui raggi cosmici di cui sopra, in particolare domande relative alle sorgenti ed ai meccanismi di accelerazione che possano
spiegare l’osservazione di particelle con energie di centinaia di EeV.
Scopo di questo lavoro è lo studio della correlazione fra le direzioni di
arrivo di raggi cosmici di energia maggiore o uguale all’EeV e le posizioni di
possibili sorgenti galattiche utilizzando i dati dell’Osservatorio Pierre Auger.
La presente relazione è organizzata nella maniera seguente:
• Il capitolo 1 fornisce una presentazione dello stato attuale della ricerca sui raggi cosmici, trattando la propagazione degli stessi nel campo magnetico galattico e le possibili sorgenti, argomenti di particolare
rilevanza per il presente lavoro.
• Il capitolo 2 funge da panoramica sulle tecniche di rilevazione dei raggi
cosmici di altissima energia e la loro implementazione presso l’Osservatorio Auger.
• Il capitolo 3 insieme al successivo rappresenta il cuore di questo lavoro.
Sono descritti qui in dettaglio lo scopo scientifico del lavoro stesso, i dati
utilizzati e la procedura di analisi degli stessi studiata e implementata
per raggiungerlo.
5
• Il capitolo 4 presenta i risultati dei metodi descritti nel capitolo precedente, vale a dire le posizioni di eccessi di eventi sulla sfera celeste e la
correlazione di queste con vari cataloghi di possibili sorgenti.
• Il capitolo 5 riassume risultati e conclusioni di questo studio e avanza
proposte per l’estensione della ricerca in questo campo.
Al termine dello studio sono stati trovati sei eccessi di eventi rispondenti
alle caratteristiche precedentemente accennate dotati di un’alta significanza.
Tuttavia essi non presentano una significativa correlazione con nessuna delle
cinque tipologie di possibili sorgenti considerate (pulsars, magnetars, LMXB,
HMXB, SNR), mentre è stata trovato un indizio di correlazione con l’area
del Centro Galattico.
6
Capitolo 1
Raggi Cosmici
A partire dalla scoperta di Victor Hess nel 1912 [19], lo studio dei raggi cosmici assunse rapidamente una grande importanza come strumento di indagine in
vari campi della fisca, particolarmente la fisica delle particelle e l’astrofisica.
A partire dallo studio delle reazioni indotte dalla radiazione di origine cosmica si arrivò nell’ambito della fisica particellare alla scoperta del positrone,
del muone e del pione. Inoltre, poichè i raggi cosmici pervengono sulla
Terra con energie sinora irraggiungibili dagli accelleratori costruiti dall’uomo, essi rappresentano un indispensabile strumento per estendere la nostra
conoscenza della fisica delle interazioni fondamentali.
Questi stessi raggi cosmici sono d’altra parte oggetto di interesse per l’astrofisca, in quanto portatori di informazione provenienti da sorgenti galattiche ed extragalattiche. In particolare i cosiddetti UHECR (ultra high energy cosmic rays), caratterizzati da energie superiori ai ∼ 1018 eV, dovrebbero puntare direttamente ai propri siti di accelerazione, fornendo una nuova
finestra di osservazione sul cosmo complementare allo studio della radiazione
elettromagnetica.
L’esistenza di UHECR di energia superiore ai 1020 eV, inizialmente riconosciuta da Linsley nel 1966 [25], è stata riconfermata da molti esperimenti
successivi. Rimangono tuttora sostanzialmente ignote però la composizione
e la natura di questi eventi, e nessun oggetto o fenomeno astrofisico è stato
chiaramente identificato come sorgente. Sono stati però elaborati con successo modelli riguardanti la propagazione dei raggi cosmici, la loro interazione
con i campi magnetici galattici ed intergalattici, e con la radiazione di fondo
cosmico. Sono stati inoltre compiuti progressi nel capire quali meccanismi
agiscano nell’accelerazione di queste particelle ad energie tanto elevate. Al7
cuni di questi modelli propongono una nuova fisica come spiegazione delle
osservazioni, come il decadimendo o l’annichilazione di particelle esotiche, e
possono essere testati sperimentalmente.
1.1
Composizione
Il flusso di raggi cosmici che investe il nostro pianeta decresce all’aumentare
dell’energia di questi ultimi, ed oltre una certa soglia (∼ 1014 eV, [11])è cosı̀
basso da richiedere tecniche di rivelazione tali da rendere estremamente difficoltosa l’identificazione delle particelle che li costituiscono. Di conseguenza,
la composizione dei raggi cosmici è sperimentalmente nota solo per basse
energie.
Fino a circa 100 GeV i raggi cosmici sono costituiti per l’ 86% da protoni,
per l’ 11% da nuclei di elio (particelle alfa), da nuclei di elementi pesanti
per l’1% e per il 2% da elettroni. Sono presenti infine anche piccole quantità di antiprotoni e positroni [31]. Fra i vari nuclidi sono particolarmente
abbondanti due gruppi di elementi: Li, Be, B e Sc, Ti, Va, Cr, Mn; al contrario idrogeno ed elio risultano essere meno abbondanti di quanto non siano
mediamente all’interno del sistema solare [6].
La relativa mancanza di questi due elementi non è del tutto compresa: potrebbe riflettere la composizione degli oggetti responsabili della loro
accelerazione, o dipendere dal fatto che elementi più pesanti sono di più
facile ionizzazione e quindi accelerazione. Invece è nota l’abbondanza di Li,
Be e B essere dovuta a processi di spallazione del carbonio e dell’ossigeno.
Questi comuni elementi possono frammentarsi durante il loro tragitto fra
la sorgente e la Terra, interagendo con l’elio e l’idrogeno del mezzo interstellare, e producendo quindi elementi più leggeri. Analogamente si spiega
l’abbondanza di Sc, Ti, Va, Cr, Mn con processi di spallazione del ferro.
La composizione dei raggi cosmici è invece simile a quella del sistema solare
nell’abbondanza di carbonio, ossigeno, azoto e ferro; in entrambe si riscontra
inoltre una relativa abbondanza o deficienza di elementi a seconda che essi
abbiano numero atomico pari o dispari, dovuta ad una maggiore o minore
stabilità degli stessi. La composizione degli oggetti sedi dei meccanismi di
accelerazione dei raggi cosmici in questa finestra energetica pare quindi non
essere dissimile da quella galattica locale. Per quanto riguarda la piccola
frazione di elettroni e positroni, i primi sono considerati di origine galattica,
ed accellerati direttamente da sorgenti primarie, mentre i secondi sono probabilmente generati secondariamente, ad esempio dalla produzione di coppie
da parte degli elettroni primari [6].
8
1.2
Lo Spettro Energetico
Lo spettro energetico caratteristico della radiazione cosmica varia su più di
30 ordini di grandezza in energie comprese fra il GeV e le centinaia di EeV,
seguendo una legge di potenza dN/dE ∼ E −α dove l’indice α assume diversi
valori in diverse finestre energetiche.
Figura 1.1: La figura mostra lo spettro energetico differenziale dei raggi
cosmici, evidenziando i punti in cui si trovano il ginocchio e la caviglia. Da
[11].
Per basse energie α assume un valore di circa 2.7. All’energia di circa
5·1015 eV compare la prima variazione dello spettro, il cosiddetto “ginocchio”
(“knee”), dove la diminuzione del flusso della radiazione si fa più rapida, con
un indice α di valore circa 3. A 5 · 1017 eV compare un secondo ginocchio
e l’indice α arriva al valore di 3.3. Infine ad energie intorno ai 1019 eV
si ha la “caviglia” (“ankle”), dove lo spettro si fa decisamente più piatto,
proseguendo con un indice α di valore circa 2.7. Il flusso decade quindi da
9
circa una particella per metro quadro per secondo a 100 GeV fino ad una
particella per kilometro quadro per anno sopra i 10 EeV [11][21].
Fino alle energie in cui è situata la caviglia si pensa che i raggi cosmici siano di origine galattica. Il modello standard per la descrizione delle
osservazioni in questa regione dello spettro, della presenza del ginocchio in
particolare, vuole che i raggi cosmici siano accellerati da processi (accelerazione secondo Fermi) aventi luogo in supernova remnants (SNR). Poichè la
massima energia raggiungibile da questi processi dipende dalla rigidità delle
particelle, l’energia di soglia, oltre la quale lo spettro diventa più ripido e il
flusso decresce più rapidamente, risulta proporzionale in questo modello alla
carica elettrica delle particelle stesse. Di conseguenza l’energia di soglia dello
spettro galattico risulta essere di circa 5 ∼ 8 · 1016 eV, vale a dire l’energia di
soglia per il ferro. Esistono vari modelli più o meno simili a questo, i quali
giungono ad una stessa forma dello spettro totale della radiazione, mentre
differiscono nel calcolo dello spettro delle singole componenti (cio lo spettro
relativo a nuclei incidenti aventi diverso numero atomico); è stato inoltre proposto che il ginocchio sia un indicazione di nuovi processi che avverrebbero
al momento dell’interazione dei raggi cosmici con l’atmosfera, processi che
involverebbero il trasferimento di parte dell’energia a particelle non osservabili (o non ancora osservate, come particelle supersimmetriche o gravitoni)
appiattendo cosı̀ lo spettro. Un’ ampia rassegna di questi modelli si può
trovare in [21].
Si pensa invece che la presenza della caviglia sia legata all’emergere alle
energie in cui essa è situata di una nuova popolazione di raggi cosmici di
origine extragalattica [20]. In questa regione lo spettro di origine extragalattica, caratterizzato da un minor indice α, attraverserebbe il più ripido spettro
galattico, cosı̀ generando la caviglia. Lo spettro extragalattico è coerente con
quello originato dall’accelerazione di particelle in fronti d’urto ultrarelativistici. Il problema è spiegare una composizione dominata da nuclei pesanti
fino a 1019 eV. La soluzione potrebbe quindi risiedere in un modello caratterizzato da una composizione mista della radiazione extragalattica, come
proposto da [3]. Un altro modello, basato su una componente extragalattica caratterizzata da protoni, spiega la caviglia attraverso la produzione di
coppie elettrone-positrone attivata dall’interezione con il fondo cosmico di
microonde [4].
1.3
Origine dei Raggi Cosmici
La determinazione di quali oggetti astrofisici siano sede dei processi che generano l’accelerazione di raggi cosmici fino alle più elevate energie e quale
10
sia l’esatta natura di questi processi è uno dei problemi fisici più difficili e
stimolanti. Molti modelli teorici sono stati proposti in questo ambito, suddividibili in tre classi principali: accelerazione da sorgenti astrofisiche (modelli “bottom-up”), non accelerazione (modelli “top-down”), e modelli ibridi
basati su entrambe le ipotesi.
Dal punto di vista sperimentale la ricerca di anisotropie significative nelle
direzioni d’arrivo degli eventi rilevati è stata effettuata da vari esperimenti,
in diversi intervalli di energia e a diverse scale angolari. La distribuzione dei
punti d’arrivo risulta sostanzialmente isotropa in un’ampia banda di energia.
Eccessi di eventi dal Centro Galattico o raggruppamenti a piccole scale angolari in corrispondenza di sorgenti compatte non sono stati confermati. Il proseguimento di questo indirizzo di ricerca con l’Osservatorio Auger dovrebbe
fornire in tempi brevi risposte non ambigue a questi interrogativi.
1.3.1
Accelerazione secondo Fermi
Un ingegnoso meccanismo stocastico adatto a spiegare l’accelerazione dei
raggi cosmici fu proposto da Enrico Fermi nel 1949 [12] [34]. Egli illustrò come
l’interazione di una particella carica con nubi di gas interstellare magnetizzate
possa condurre ad un guadagno di energia per la particella.
Si assuma che una particella relativistica di energia E0 incontri una nube
di grande massa dotata di un campo magnetico caotico. Poichè la particella
è relativistica E0 ' p0 , mentre la massa della nube è infinita rispetto a quella
della particella, e la sua velocità vale βcl . La particella penetra nella nube
con angolo θ1 rispetto alla velocità della nube e diffonde sulle irregolarità del
campo magnetico al suo interno, quindi ne fuoriesce con angolo θ2 . L’energia
iniziale della particella nel sistema di rifermiento della nube è:
E0∗ = γcl E0 (1 − βcl cosθ1 ),
dove γcl è il fattore di Lorentz relativo alla nube, mentre l’energia finale
nel sistema di laboratorio vale:
E1 = γcl E1∗ (1 + βcl cosθ2∗ ),
E0∗
Siccome le collisioni della particella all’interno della nube sono elastiche,
= E1∗ . Da ciò risulta:
1 − βcl cosθ1 + βcl cosθ2∗ − βcl2 cosθ1 cosθ2∗
∆E
=
− 1.
E
1 − βcl2
È necessario ora mediare su tutte le possibili direzioni di entrata e di uscita
della particella ripetto alla nube. A causa della natura casuale delle collisioni
11
della particella all’interno della nube, < cosθ2∗ >= 0, mentre la media sulla
direzione d’entrata dipende dalla velocità relativa dei due oggetti: assumendo
βcl 1 risulta < cosθ1 >= −βcl /3. Da ciò risulta un guadagno medio di
energia pari a:
∆E
4
' βcl2 .
E
3
Questo meccanismo è tuttavia poco efficiente, poichè il guadagno energetico ad ogni collisione nube-particella è quadratico rispetto a βcl . Siccome
il valore di βcl è molto piccolo, l’accelerazione ad energie elevate richiederebbe
un grande numero di interazioni ed un tempo elevato.
Un meccanismo simile ma più efficiente fu proposto negli anni ’70 [34]:
l’accelerazione di raggi cosmici in fronti d’urto generati da fenomeni energetici
come nove, supernove, AGN e simili. Un simile fronte è generato dall’espandersi del materiale espulso dalla sorgente a velocità vr molto maggiore della
velocità del suono nel mezzo interstellare. La velocità vs del fronte dipende
R
vr . Una particella può difda vr e dal rapporto di compressione R: vs = R−1
fondere sulle irrogolarità magnetiche del mezzo interstellare e attraversare il
fronte. A prescindere dalla direzione di attraversamento, essa vede la materia
dall’altro lato avvicinarsi a velocità vr , perciò ad ogni attraversamento del
fronte vi è un guadagno di energia. Detti ora θ2∗ e θ1 gli angoli di attraversamento della direzione della particella rispetto al piano del fronte dalla parte
posteriore del fronte a quella anteriore e viceversa rispettivamente, si possono
calcolare i valori medi < cosθ2∗ >= 2/3 e < cosθ1 >= −2/3. Dalla formula
precedente si ha ora per il guadagno di energia ad ogni passaggio del fronte:
4
∆E
' βcl ,
E
3
vale a dire esso è ora del primo ordine in βcl , ed il mecanismo di accelerazione è quindi molto più efficiente.
1.3.2
Sorgenti Astrofisiche
La forma regolare dello spettro dei raggi cosmici entro un ampio intervallo
di energia suggerisce un meccanismo di accelerazione comune che potrebbe
aver luogo in diversi oggetti e fenomeni astrofisici. Sono stati avanzati molti
modelli e proposte diverse sorgenti capaci di accelerare particelle ad energie
eccedenti l’EeV, ma a tutt’oggi nessuno è stato verificato sperimentalmente.
Vi sono basilarmente due meccanismi di accelerazione riguardanti i raggi
cosmici: accelerazione diretta di particelle cariche da parte di campi elettromagnetici ed accelerazione stocastica secondo Fermi, avente luogo in nubi
12
Figura 1.2: Rappresentazione grafica dell’accelerazione di raggi cosmici in
fronti d’urto. Da [34].
magnetizzate. In entrambi i casi l’energia massima delle particelle che una
data sorgente può generare impone dei limiti all’intensità dei campi magnetici presenti in quella regione di spazio e alle dimensioni della regione stessa.
Detta Emax l’energia massima che un dato oggetto oggetto astrofisico può
conferire a particelle cariche, essa può essere raggiunta solo se le particelle
in questione rimangono confinate nella regione di spazio assegnata [34]. In
altri temini il raggio di girazione delle particelle all’interno del campo magnetico della sorgente deve essere minore o uguale alle dimensioni lineari della
sorgente stessa:
Emax = γqBR
dove B è l’intensità del campo magnetico della sorgente, R il suo raggio,
q la carica della particella e γ il fattore di Lorentz del mezzo in cui avviene
l’accelerazione.
Data quindi una certa specie di particelle (e specificatane la carica elettrica) di data energia, si possono determinare quali oggetti possano costituirne
i siti di accelerazione. Tali considerazioni possono essere riassunte nel grafico
detto plot di Hillas, in cui in scala bilogaritmica vengono riportate in ordinate
l’intensità del campo magnetico ed in ascisse le dimensioni lineari di varie
possibili sorgenti. Quelle in alto a destra, al di sopra della zona ombreggiata
soddisfano i requisiti necessari ad accelerare protoni ad energie di 100 EeV,
mentre la linea più scura rappresenta il limite per l’accelerazione di nuclei di
ferro a 100 EeV.
Come si può vedere esistono nel primo caso solo quattro tipi di sistemi che
possano essere responsabili per questo fenomeno: stelle di neutroni dotate
di grande campo magnetico, nuclei galattici attivi, lobi di radiogalassie e
fronti d’urto su scale del gigaparsec nel mezzo extragalattico. È utile una
panoramica sulle varie tipologie di sorgenti che si trovano in letteratura:
13
Figura 1.3: Plot di Hillas. La parte superiore della banda ombreggiata rappresenta il limite inferiore per l’accelerazione di protoni a 100 EeV, la linea
scura il limite inferiore per nucledi di ferro a 100 EeV. Da [34]
• Fronti d’urto associati alla formazione di strutture su larga scala. Simili
fronti possono formarsi a causa dell’attrazione gravitazionale e generare
in principio campi magnetici. L’energia massima è dipendente dalle
dimensioni del fronte: assumendo valori del nanogauss per i campi
extragalattici e del microgauss per i campi generati dal fronte, essa
eccede i 1020 eV per dimensioni di 50 Mpc.
• Ammassi di galassie. Sono stati osservati in questi sistemi campi magnetici di 5 µG su distanze di 500 kpc, e ciò porta ad una energia
massima di 1020 eV.
• Radiogalassie. In particolare galassie di tipo FR II presentano lobi di
dimensioni fino a 100 kpc e campi stimati in 10 µG, per energie massime
intorno ai 1021 eV.
• Nuclei galattici attivi. In principio qualunque AGN potrebbe essere
sorgente di UHECR, visti i campi di circa 5 G in volumi delle dimensioni
di 0.02 pc, nei pressi del buco nero centrale. Il problema sono le ampie
perdite di energia nella zona centrale dell’AGN.
• Gamma-ray bursts. Nei jet relativistici (γ = 100 ∼ 1000) dei GRB
potrebbero avere luogo efficienti processi di accelerazione di UHECR.
14
La principale obiezione sono le distanze cosmologiche di questi oggetti
che li rendono sorgenti poco probabili a causa dell’effetto GZK.
• Collisioni di galassie. Il movimento delle galassie all’interno degli ammassi e le loro collisioni potrebbero generare ampi fronti d’urto. Fronti
di dimensioni pari a 30 kpc e campi magnetici di 20 µG potrebbero
accelerare raggi cosmici fino a 1020 eV.
• Buchi neri non attivi. è stato suggerito che l’accelerazione di UHECR
potrebbe avvenire all’orizzonte degli eventi di buchi neri massivi in
rotazione. Il modello richiede buchi neri di almeno un miliardo di masse
solari entro 50 Mpc dalla Terra.
Altre possibili sorgenti particolarmente rilevanti per il presente lavoro
(pulsars,magnetars,LMXB,HMXB,SNR) sono trattate in maggiore dettaglio
nel quarto capitolo.
1.4
1.4.1
Propagazione dei Raggi Cosmici
Effetto dei campi magnetici
Durante il tragitto fra il sito di accelerazione e la Terra i raggi cosmici
sono naturalmente deflessi dalla presenza di campi magnetici. L’intensità
di questi campi viene determinata dallo studio della rotazione del piano di
polarizzazione della radiazione elettromagnetica emessa da lontane sorgenti
extragalattiche come pulsar o sorgenti radio. Campi magnetici intergalattici
regolari sono fortemente limitati a valori di circa 10−9 G o inferiori da queste
misure, mentre ammassi di galassie potrebbero avere campi magnetici più
intensi coerenti sulla scala del megaparsec.
È noto che il campo magnetico della nostra Galassia possiede una struttura regolare su grande scala. Esso mostra un intensità tipica di alcuni microgauss, approssimativamente uniforme su distanze di qualche kiloparsec.
Le linee di forza di questo campo seguono la struttura a spirale dei bracci
galattci. Vari modelli del campo esistono che differiscono per il segno del
campo nei bracci e per la simmetria rispetto al piano galattco [17].
L’entità della deflessione subita da un raggio cosmico che interagisca con
il campo magnetico galattico dipende dalla sua rigidità. Protoni di energia 1
EeV sono intrappolati nelle strutture del campo magnetico stesso e assumono
una traiettoria elicoidale spiraleggiante intorno alle linee di forza. Il raggio di
girazione di questa traiettoria per un campo di 3 µG è approssimativamente
300 pc, circa lo spessore del piano galattico. Protoni di energia maggiore
15
Figura 1.4: La figura mostra le traiettorie seguite da protoni nel campo
magnetico galattico. Le linee continue rappresentano protoni da 1 EeV,
quelle tratteggiate protoni da 10 EeV. Da [17].
o uguale a 10 EeV (o particelle di ancora maggiore rigidità) invece sono
poco influenzate dalla presenza del campo magnetico, avendo un raggio di
girazione il cui ordine di grandezza è pari a quello della distanza percorsa.
In questo caso l’informazione sulla direzione originaria della particella viene
preservata ed possibile ricostruirla. La quantità chiave per determinare
la deflessione angolare rispetto alla direzione di provenienza è il raggio di
girazione (o di Larmor) della particella rL ' E/(Z · B⊥ ), dove Z è la carica
della particella e B⊥ la componente del campo magnetico perpendicolare al
momento della particella. Assumendo un campo magnetico costante lungo
la distanza percorsa d, si ottiene:
E
dθ(E, d) ' d/rL ' 0.52 · Z ·
100 EeV
◦
−1 ·
B
10−9
d
·
G
M pc
!
Questo equivale ad una deviazione di meno di 1◦ per un protone da 100
EeV su una disanza di un kiloparsec in un campo di 1 µG, o equivalentemente
una distanza di un magaparsec in un campo di un nG [7][29].
1.4.2
L’effetto GZK
Alle più alte energie alle quali vengono accellerati i raggi cosmici non solo
l’interazione con i campi magnetici gioca un ruolo importante nello studio
16
della loro propagazione, ma anche l’interazione con la radiazione cosmica
di fondo di microonde, infrarossa e radio. Ciò presenta ripercussioni anche
per l’interpretazione dello spettro energetico. A seguito della scoperta del
fondo cosmico di microonde (da parte di Penzias e Wilson [30]), Greisen
[16], Zatsepin e Kuz’min [23] predissero una forte soppressione del flusso di
protoni a partire da energie di circa ∼ 5 · 1019 eV a causa di processi di
fotoproduzione di pioni per intereazione sul CMB. I principali processi che
coinvolgono i protoni in questo range di energie sono:
p + γCM B −→ p + π 0
p + γCM B −→ n + π +
p + γCM B −→ p + e+ + e− .
Nel sistema di riferimento di laboratorio, l’energia al quadrato del sistema
vale:
s = m2p + 2Ep (1 − β cos θ),
dove è l’energia del fotone, θ è l’angolo di incidenza fra protone e fotone e
c = 1. L’energia di soglia perché questo processo avvenga in una collisione
frontale e considerando una tipica energia per il fotone di ∼ 6·10−4 eV risulta
essere circa ∼ 1020 eV, ma può essere anche inferiore poichè lo spettro del
CMB si estende fino ad energie di circa ∼ 10−3 eV.
La lunghezza di interazione per i protoni si può ricavare nota la sezione
d’urto di questo processo e la densità di fotoni del fondo cosmico, e risulta
pari a:
1
' 8 M pc
λp =
σ · nCM B
Poichè la perdita di energia del protone per ogni collisione è di circa il 20%,
la lunghezza di attenuazione oltre la quale essa scende al di sotto dell’energia
di soglia necessaria perché il processo di fotoproduzione avvenga si aggira
su alcune decine di Mpc. Questo porta come conseguenza che le sorgenti
di UHECR di energie superiori al cutoff GZK devono essere contenute in
una sfera di raggio non superiore a questo valore, altrimenti la loro energia
verrebbe dissipata prima che essi possano raggiungere la Terra.
1.4.3
Propagazione di neutroni e fotoni
Come detto precedentemente è di grande importanza al fine di compiere studi
relativi ai siti di accelerazione tenere conto dell’effetto dei campi magnetici
nella propagazione dei raggi cosmici carichi. Ciò vale in particolare per particelle di energia relativamente bassa (E < 10 EeV) e di origine verosimilmente
17
Figura 1.5: Andamento dell’energia dei protoni in funzione della distanza
secondo l’effetto GZK. Si noti come quale che sia l’energia di partenza, a
circa 100 Mpc dalla sorgente essa scenda a ∼ 1020 eV. Da [11].
galattica quali quelli di interesse per il presente lavoro. La ricerca in questo
settore si muove in due direzioni strettamente legate: da un lato si cerca
di capire l’effetto del campo magnetico galattico sulla distribuzione delle direzioni di provenienza dei raggi cosmici, dall’altro si inverte il procedimento
per ricavare informazioni sul campo nota la distribuzione dei raggi.
In generale comunque per il range di energie in questione si è visto come
la presenza del campo magnetico galattico isotropizzi sostanzialmente la distribuzione dei raggi cosmici: ne segue che eventuali eccessi di misure in date
direzioni devono essere dovuti a perticelle neutre, non influenzate dal campo
magnetico. In particolare i candidati principali sono neutroni e fotoni. Essi
possono propagarsi in linea retta e rilevandoli all’arrivo sulla Terra è in linea
di principio possibile risalire alla loro sorgente.
Bisogna tuttavia tenere conto delle altre possibili interazioni che interessano fotoni e neutroni e che possono impedirne la propagazione indisturbata
fin sul nostro pianeta. Per i neutroni in particolare il problema principale è
l’instabilità: un neutrone libero effettua decadimento β con una vita media di
circa 15 minuti. Se si considera però l’effetto della dilatazione temporale per
un neutrone ultrarelativistico (E ' 1 EeV) risulta che esso può propagarsi in
media per ∼ 10E kpc prima di decadere, vale a dire possono giungere sulla
18
Terra neutroni di 1 EeV prodotti entro una sfera di raggio pari a 10 kpc, o
più estesa se l’energia è superiore. Tenendo conto che il raggio della Galassia
è approssimativamente pari a 15 kpc e la Terra dista da Centro Galattico
circa 8 kpc, possono giungere sulla Terra neutroni da quasi qualunque punto
della Galassia.
Per quanto riguarda i fotoni, vi sono invece argomenti che sembrano suggerire una più difficile propagazione oltre energie pari a circa 1014 . Innanzitutto i fotoni interagiscono più facilmente con il mezzo interstellare ed in
particolare possono essere in alcuni casi completamente schermati da nubi di
polvere. Inoltre ad energie cosı́ elevate possono indurre cascate elettromagnetiche a partire dalla produzione di coppie elettrone-positrone. I limiti attuali
sulla frazione di fotoni nel flusso di raggi cosmici nella regione dell’EeV sono
pari al 2-3 % [2].
19
20
Capitolo 2
Rivelazione dei raggi cosmici e
l’Ossevatorio Pierre Auger
Ad energie di circa 1014∼15 eV il flusso di raggi cosmici incidenti sulla Terra si riduce notevolmente, fino a valori dell’ordine di un evento per metro
quadro per anno. Risulta perciò impraticabile la rivelazione diretta, tipicamente a mezzo di piccoli rivelatori allogiati in satelliti artificiali e posti
al di sopra dell’atmosfera. Vengono sfruttate invece tecniche di rivelazione
sensibili ai prodotti dell’interazione fra i raggi cosmici e le molecole dell’atmosfera, e costruiti rivelatori dotati di una grande superficie di raccolta cosı̀
da controbilanciare la poca entità del flusso.
La prima rivelazione di questi prodotti secondari, oggi denominati cascate
di particelle (extensive air showers, EAS) fu effettuata da Pierre Auger nel
1939 [5]. Egli riportò l’osservazione di segnali coerenti in contatori disposti
a varie altezze su un ampia area, dimostrando la presenza di raggi cosmici
primari di energie di circa ∼ 1015 eV.
Da allora è ampiamente cresciuto l’interesse verso lo studio di questi
fenomeni, e parallelamente si è assistito allo sviluppo delle tecniche sperimentali necessarie a supportare tale studio. Col tempo è cresciuta la dimensione
dei rivelatori, in modo da soddisfare i requisiti relativi all’apertura del campo di vista e all’efficienza del processo di rivelazione. è stata inoltre messa
a punto la tecnica di rivelazione di fluorescenza, che consente di studiare lo
sviluppo del profilo longitudinale degli sciami grazie alla luce prodotta da
questi durante l’attraversamento dell’atmosfera.
L’Osservatorio Pierre Auger occupa una posizione di punta in questo
panorama, specialmente per la combinzione di entrambe le tecniche sopra
21
citate, cosa che permette di ottenere misure indipendenti delle stesse quantità
e di effettuare una calibrazione incrociata dei rivelatori.
2.1
Fisica degli sciami di particelle atmosferiche
Un raggio cosmico costituito da un nucleone o nucleo atomico al raggiungimento della Terra incide sugli strati più alti dell’atmosfera, interagendo con
le molecole presenti in essa. Risultato dell’interazione è la produzione di un
grande numero di particelle secondarie, le quali ricevono parte dell’energia
del raggio cosmico primario, propagandosi verso la superficie terrestre ed interagendo a loro volta con l’atmosfera: questo scenario viene indicato con il
nome di cascata o sciame di particelle.
Una cascata attraversa l’atmosfera terrestre raggiungendo il massimo
sviluppo ad una certa profondità che dipende dall’energia e dalla tipologia del primario che l’ha generata; in seguito l’energia delle particelle che la
compongono scende sotto la soglia critica necessaria alla produzione di nuove
particelle, la cascata progressivamente si attenua.
Il comportamento di una cascata è determinato dalle caratteristiche del
primario (energia, tipo di particella, direzione di impatto sull’atmosfera. . . ),
dunque in linea di principio è possibile ricostruirele studiando le particelle
secondarie che esso genera nell’atmosfera. L’interpretazione di questi eventi
è però difficoltosa. Gli apparati registrano particelle che attraversano quasi
contemporaneamente il piano di rivelazione, energia e tipo del raggio cosmico vanno ricavate dal numero di particelle della cascata e da altri parametri,
ma poichè il punto di origine di quest’ultima è ignoto ne va prima stimato
il grado di sviluppo. Inoltre una cascata è usualmente divisa in tre componenti: una elettromagnetica composta di fotoni, elettroni e positroni; una
muonica, composta da muoni; ed una adronica, in cui rientrano tutte le altre
particelle (pioni per la maggior parte). Non è ugualmente facile modellizzare
efficacemente lo sviluppo di tutte le tre componenti.
In pratica la ricostruzione delle cascate viene effettuata mediante metodi Monte Carlo, in cui le caratteristiche dello sciame sono confrontate con
modelli teorici per risalire alle caratteristiche del primario. Risultati possono essere raggiunti sulla base di un numero statisticamente significativo di
eventi.
Anche questi metodi presentano tuttavia delle difficoltà: la natura delle
interazioni adroniche ad energie elevate non è infatti nota, ma viene estrapolata da valori misurati a più basse energie. Differenti estrapolazioni por22
tano di conseguenza a differenti ricostruzioni degli sciami e differenti stime
riguardo le caratteristiche dei primari.
Nonostante queste difficoltà è tuttavia possibile stimare con precisione
soddisfacente energia e direzione d’arrivo dei UHECR, e prosegue il lavoro
sulla discriminazione di adroni e fotoni e su tecniche di rivelazione della
componente muonica degli sciami.
2.1.1
Il modello di Heitler per le cascate elettromagnetiche
Un modello molto semplice ma efficace per la descrizione delle cascate elettromagnetiche è quello proposto da Heitler [34][18].
Egli descrive uno sciame consistente di particelle dello stesso tipo, ciascuna delle quali è caratterizzata da una lunghezza di interazione λ. Ad ogni
interazione, due nuove particelle vengono create, ciscuna di energia pari alla
metà dell’energia della particella primaria che le ha generate.
Figura 2.1: Rappresentazione grafica del modello di Heitler. Da [34].
Partendo da una singola particella di energia E0 , dopo una lunghezza di
interazione si avranno quindi due particelle di energia E = E0 /2, dopo una
lunghezza pari a 2λ si avranno 22 particelle di energia E = E0 /22 , ed in
generale dopo N interazioni, cioè dopo N λ in termini spaziali, si avranno 2N
particelle di energia E = E0 /2N . Questo processo prosegue finchè l’energia
delle particelle secondarie non scende sotto una certa soglia critica Ec , alla quale la sezione d’urto di produzione di nuove particelle si annulla. A
questo punto il numero di particelle non cresce più, il modello di Heitler si
interrompe e lo sciame si attenua. Dunque il numero massimo di particelle
di uno sciame è pari a Nmax = E0 /Ec , e viene raggiunto ad una profondità
Xmax = λ log 2E0 /Ec .
23
Secondo il modello di Heitler la profondità di massimo sviluppo di uno
sciame è proporzionale al logaritmo dell’energia del primario ed il numero
di particelle a questa profondità è direttamente proporzionale all’energia del
primario. Benchè questo modello sia molto semplice esso descrive in maniera
qualitativamente corretta lo sviluppo degli sciami elettromagnetici. Ciò è
principalmente dovuto al fatto che per energie al di sopra di 1 MeV i processi
dominanti sono la radiazione di bremsstralhung per elettroni e positroni e la
produzione di coppie per i fotoni, e questi processi sono caratterizzati da
un’unica lunghezza di interazione λ.
In prima approssimazione questo modello è valido anche par cascate
adroniche. Si consideri un raggio cosmico primario di energia E0 costituito
da un nucleo di numero atomico A. Allora si può immaginare di modellizare
lo sciame risultante come la sovrapposizione degli sciami prodotti separatamente da ciascun nucleone, dove i nucleoni hanno energia E ∗ = E0 /A. Il
punto di massimo sviluppo dello sciame sarà dato da Xmax = λ log 2E0 /A,
vale a dire lo sviluppo massimo sarà raggiunto prima nel caso di un nucleo
con elevato valore di A piuttosto che che da un singolo nucleone, a parità di
energia.
2.1.2
Sciami adronici
Uno sciame adronico viene avviato dall’interazione di un nucleo o un nucleone
su di un nucleo atmosferico. In entrambi i casi circa la metà dell’energia totale
viene trasferita a mesoni secondari, principalemente pioni neutri e carichi. In
questo processo il numero di pioni carichi è circa due volte il numero di pioni
neutri. Il resto dell’energia iniziale si trova in un nucleone secondario, il
quale dopo aver percorso mediamente una lunghezza di interazione produce
a sua volta una seconda cascata di pioni. Nel frattempo i pioni di prima
generazione interagiscono accrescendo lo sciame, e questo processo continua
fino a che l’energia non scende al di sotto della soglia critica di interazione
[34].
A meno di non avere energia estremamente alta, i pioni neutri decadono
quasi immediatamente in fotoni, essendo caratterizzati da una lunghezza di
interazione pari circa 10−8 m. I fotoni iniziano quindi degli sciami elettromagnetici. I pioni carichi invece hanno una lunghezza di interazione molto maggiore, circa 7.8 m: essi possono decadere o interagire di nuovo. Lo sviluppo
longitudinale dello sciame è determinato quindi dai dettagli dell’interazione
e del decadimento dei pioni: pioni carichi di alta energia tendono ad interagire, mentre pioni di bassa energia tendono a decadere in muoni e neutrini
muonici. Il quadro è complicato dal variare del comportamento delle parti24
celle al variare delle densità atmosferica man mano che lo sciame prosegue
verso terra.
Una parametrizzazione dello sviluppo longitudinale del fascio è stata
proposta da Gaisser e Hillas [34] nella forma:
N (X) = Nmax
X − X1
Xmax − λ
−λ
Xmax
λ
X − X1
· exp −
λ
dove X1 è il punto di prima interazione del primario nell’atmosfera. Questa formula è un fit standard per lo sviluppo longitudinale degli sciami.
Analogamente è stata sviluppata da Greisen e Nishimura-Kamata una
teoria che conduce ad una parametrizzazione per la distribuzione laterale del
fascio, vale a dire la densità di particelle ad una distanza r dall’asse del fascio
al livello del suolo. Essa è:
C1 (s)Ne
ρ(r) =
2πr12
r
r1
s−2 r
1+
r1
s−9/2
1 + C2
r
r1
δ !
dove il parametro r1 è detto raggio di Molière.
2.2
Rivelatori di superficie
L’idea alla base della progettazione dei rivelatori di superficie (surface detectors, SD) è molto semplice: si tratta di attrezzare una area opportunamente
scelta con dei rivelatori che permettano di campionare le particelle di uno
sciame, in modo da poterne stimare numero, natura, direzione di arrivo e
correlare poi queste caratteristiche a quelle del primario.
Questo metodo presenta il chiaro vantaggio di poter in principio disporre
di una superficie di raccolta molto ampia, cosı́ da aumentare l’esposizione
e poter rivelare un numero statisticamente significativo anche di eventi di
altissima energia, per cui il flusso è molto basso. Naturalmente vari motivi,
principalmente economici, impediscono di ricoprire l’intera area disponibile
con rivelatori. Essi, di superficie pari a qualche metro quadro, sono posti
invece ad una certa distanza l’uno dall’altro secondo una configurazione regolare. La distanza fra i rivelatori è frutto di un compromesso fra i costi di
costruzione, l’area da ricoprire e la distribuzione laterale degli sciami che si
cerca di rivelare. Un altro parametro di cui tenere conto è l’altezza del rivelatore sul livello del mare: essa deve corrispondere alla profondità alla quale
gli sciami di energia di interesse raggiungono il massimo sviluppo. I rivelatori di cui l’apparato è costituito sono generalmente rivelatori Cherenkov o
scintillatori.
25
Figura 2.2: Disposizione geografica e geometrica dei rivelatori di superficie
dell’Osservatorio Auger. Da [34].
Il sito sud dell’Osservatorio Pierre Auger dispone di un rivelatore di superficie costituito da 1600 detector Cherenkov, separati da circa 1.5 km e disposti su di una griglia triangolare regolare che si estende per circa 3000 km2 ,
ad una altezza media di 1400 m sul livello del mare. Altezza e distanza
dei rivelatori sono state studiate per ottenere piena efficienza per sciami di
energia maggiore o uguale a 10 EeV. Ciascun detector è costituito da una
tanica di acqua di 3.6 m di diametro e 1.2 m di profondità, per un volume
di 12 m3 e una superficie di raccolta di 10 m2 . All’interno di ogni tanica
sono presenti 3 tubi fotomoltiplicatori da 200 mm di diametro per la rivelazione della luce Cherenkov, mentre all’ esterno si trovano i pannelli solari e
le batterie necessarie all’alimentazione dell’elettronica e le antenne di comunicazione: un antenna radio per la trasmissione del segnale ed una GPS per
la sincronizzazione. L’acqua è deionizzata e purificata al fine di ottenere la
massima lunghezza di attenuazione per la luce Cherenkov, inoltre il rivestimento interno delle taniche è costituito da polietilene e tyvek, materiale che
garantisce una riflettività prossima al 100% [32].
Dall’analisi dei segnali rilevati da ciascun detector è possibile ricavare i
parametri di un fascio e da questi le caratteristiche del primario. Il primo passo è la determinazione della direzione dell’asse del fascio in termini
dell’angolo zenitale ed azimutale. ciò si ricava dal confronto fra i tempi di
arrivo del fascio su almeno tre detector non allineati: ad esempio detta dij
la distanza fra due rivelatori e tij l’intervallo di tempo trascorso fra i segnali
26
registrati, l’angolo zenitale si ricava come
ctij
θ = arcsin
dij
!
.
La risoluzione angolare dipende dal numero di particelle rilevate e dalla
risoluzione temporale dei rivelatori, e nel caso dell’Osservatorio Auger raggiunge valori tipici di 1◦ . Stabilita la direzione di arrivo è possibile trovare il
core del fascio, cioè il punto di intersezione fra l’asse ed il terreno, che non
è possibile stabilire a priori dalla direzione del fascio perché la distribuzione
NKG è definita sul piano perpendicolare all’asse, non sul piano del terreno.
A questo punto è possibile stimare il numero di particelle di cui il fascio è
costituito e ricavarne il valore dell’energia del primario.
2.3
Rivelatori di fluorescenza
Le particelle energetiche di uno sciame nel transitare attraverso l’atmosfera
eccitano le molecole di azoto in essa presenti, e la successiva diseccitazione di
queste molecole avviene mediante emissione di quella che viene chiamata luce
di fluorescenza. Sotto opportune condizioni sperimentali (principalmente climatiche), è possibile rilevarla e ricavare informazioni sullo sciame che l’ha
prodotta.
Lo schema concettuale di un rivelatore in grado di effettuare questa
misura è molto semplice: si tratta di un telescopio che focalizzi la luce di
fluorescenza su di un array di fototubi che la rivelino. Le condizioni necessarie al funzionamento di questi sistemi sono: assenza di fonti luminose
nel campo di vista del telescopio, cielo limpido ed assenza di perturbazioni
atmosferiche. Praticamente ciò significa che buone misure possono essere effettuate solamente di notte, con cielo non nuvoloso ed evitando il disturbo
della luce lunare. Di conseguenza il duty cycle di questi rivelatori è molto
basso.
L’Osservatorio Auger dispone di quattro stazioni per la rivelazione della
luce di fluorescenza da sciami atmosferici. Ciascuna è dotata di sei telescopi,
per un campo di vista di 180◦ in azimuth e 30◦ in elevazione. Ogni telescopio è
costituito da uno specchio sferico, un diaframma per eliminare le aberrazioni
da coma, un filtro che trasmette luce con lunghezza d’onda compresa fra circa
300 e 400 nm per l’eliminazione del fondo luminoso ed un anello collettore
per la riduzione dell’aberrazione sferica. La luce viene riflessa da questo
sistema su di un array di 440 tubi fotomoltiplicatori, ed i dati acquisiti sono
trasmessi da un collegamento wireless al CDAS (Central Data Acquisition
27
Figura 2.3: A sinistra rappresentazione della traccia vista da un rivelatore
di fluorescenza sull’array di PMT. A destra visualizzazione della traiettoria
dello sciame vista dal telescopio. Da [34].
System) [32]. Il duty cycle è pari circa al 12%. È infine presente una facility
laser nel centro dell’Osservatorio per la calibrazione del sistema.
La luce di fluorescenza è emessa in modo isotropo da ogni punto dello sciame, quindi i rivelatori FD possono effettuare misure anche su sciami
il cui core non cada vicino alla posizione del telescopio. Essi vedono uno
sciame come un punto in moto alla velocià della luce che lascia una traccia
in coordinate celesti sull’array di fototubi. Le grandezze più importanti da
determinare nell’analisi di uno sciame sono il parametro d’impatto R⊥ , cioè
la minima distanza fra la traiettoria dello sciame e il rivelatore, e il piano
definito dalla traiettoria dello sciame e il punto in cui si trova il telescopio.
Risulta a questo punto facile determianare la traiettoria se la rivelazione è
stata stereoscopica, cioè se lo sciame è stato visto da due rivelatori posti in
locazioni diverse. L’incertezza è molto più grande se sono disponibili dati da
un solo rivelatore. Determinati i paramtetri geometrici dello sciame è possibile studiarne lo sviluppo longitudinale. La stima della luce emessa lungo
l’asse dello sciame viene effettuata integrando i segnali dei fotomoltiplicatori nell’intervallo di tempo in cui la traccia permane nel campo di vista di
ciascuno di essi, tenendo ovviamente conto della loro effcienza quantica e
dellattenuazione atmosferica, continuamente monitorata. Il numero di fotoni
raccolti da uno specchio è pari a:
A
T (r)∆L
4πr2
dove Ne è il numero di particelle cariche del fascio (nell’angolo sotteso
dalla traccia vista dal rivelatore), A l’area del telescopio, r la distanza dallo
Nγ = Ne Yγ
28
sciame, T (r) una funzione che descrive la propagazione luminosa nell’atmosfera e ∆L la lunghezza della traccia sull’array di PMT e Yγ il numero di
fotoni prodotti da una particella carica per unità di cammino percorso (resa
luminosa). Nota Yγ è possibile trovare Ne in funzione di X (profondità dello
sciame nell’atmosfera), cioè il profilo longitudinale. Integrandolo è possibile
stimare l’energia del primario:
E=α
Z +∞
0
Ne (X)dX
dove α è un parametro che dipende dall’energia critica dell’elettrone e
2
dalla lunghezza di radiazione in aria, e vale circa 2 M eVg cm . A questa energia
va applicata una correzione del 10% dovuta al contributo di particelle non
rilevabili come neutrini e muoni, che essendo più penetranti non rilasciano
energia nell’atmosfera.
29
Figura 2.4: Rappresentazione grafica di un evento visto dal rivelatore di superficie e dalle quattro stazioni di fluorescenza dell’Osservatorio Pierre Auger.
Da sito ufficiale dell’Osservatorio, http://www.auger.org/
30
Capitolo 3
Identificazione di eccessi di
raggi cosmici nella regione
dell’EeV
Raggi cosmici di energia poco superiore ai 1018 eV sono ritenuti essere in
grande maggioranza di origine galattica, e considerato il grande volume di
dati raccolti da esperimenti come l’Osservatorio Auger è possibile cercare di
identificarne le sorgenti.
Come illustrato nei capitoli precedenti, la maggior parte degli eventi rilevati è quasi certamente dovuta a particelle cariche, protoni e nuclei. Per
energie simili a quelle considerate d’altro canto la rigidità magnetica di queste
particelle è sufficientemente bassa da risultare in una notevole deflessione da
parte del campo magnetico galattico durante il tragitto fino alla Terra. Di
conseguenza l’informazione riguardante il punto d’origine di queste particelle
è persa, e si può assumere che esse giungano sulla Terra con una distribuzione
isotropa.
Questo tuttavia non vale per particelle neutre, cioè in questo caso neutroni e fotoni: questi viaggiano in linea retta nei campi magnetici, preservando
l’informazione riguardante la posizione della sorgente. La produzione di neutroni aqueste energie è più efficiente di quella di fotoni, e questi ultimi sono
inoltre facilmente schermati dal materiale interstellare. I neutroni effettuano
decadimento β con una vita media di circa 15 minuti, durante la quale coprono distanze di circa 10 E kpc, dove E è espresssa in EeV. Di conseguenza
essi possono giungere sulla Terra da qualsiasi punto della Galassia.
Con questo lavoro si è cercato quindi di identificare sorgenti galattiche
puntiformi di neutroni di energia 1 EeV o superiore.
31
3.1
Il campione di dati
È stato selezionato un campione di dati fra gli eventi rivelati dall’Osservatorio Pierre Auger fra gennaio 2004 e dicembre 2009, estratti dal catalogo
ufficiale dela collaborazione (Herald v4r6p3). La principale caratteristica del
campione è il limite inferiore imposto all’energia degli eventi, 1 EeV.
Altri criteri di selezione sono stati implementati allo scopo di disporre di
eventi per cui fosse disponibile una ricostruzione qualitativamente soddisfacente; ad esempio è stato richiesto che per ciascun evento la stazione che ha
registrato il segnale più intenso fosse circondata da un esagono di 6 stazioni
funzionanti; si sono considerati solamente eventi caratterizzati da un angolo
zenitale inferiore a 60◦ ; sono inoltre stati esclusi eventi rivelati durante i “bad
periods”, intervalli di tempo durante i quali il segnale prodotto dal rivelatore
non è stato giudicato attendibile.
In totale il numero di eventi rispondente a questi criteri è risultato essere
278724.
3.2
Significanza secondo Li-Ma
Al fine di caratterizzare gli eccessi di eventi in quanto tali e poter quindi
stimare la probabilità che l’osservazione di un eccesso non sia dovuta ad una
fluttuazione statistica nei dati si è scelto come parametro la significanza di
Li e Ma [24], originariamente introdotta per studi di astronomia gamma.
Dato un detector che osserva un certo numero di eventi Non in un tempo
ton per poi effettuare una misura di background di Nof f eventi in un tempo
tof f , la significanza S di un eventuale eccesso di eventi è definita come:
S=
√
(
2 Non ln
"
#
"
Nof f
1+α
Non
+ Nof f ln (1 + α)
α
Non + Nof f
Non + Nof f
#) 1
2
dove α = ton /tof f . La significanza cosı́ definita risulta da simulazioni
Monte Carlo avere una distribuzione molto vicina ad una curva gaussiana di
valor medio nullo e varianza unitaria. Di conseguenza la probabilità che una
reale sorgente esista nella direzione di osservazione, può essere valutata come
p = 1 − ξ, dove ξ è il valore della distribuzione normale valutata per il valore
di S misurato.
La significanza S può essere facilmente adattata allo studio dei raggi cosmici: data una certa cella di osservazione centrata in un punto (α, δ) della
sfera celeste (α e δ rappresentano rispettivamente l’ascensione retta e la declinazione) e di raggio angolare θ, Non sarà il numero di raggi cosmici di data
32
energia provenienti da quella cella e Nof f il numero di eventi di background
attesi in quella cella calcolati secondo l’accettanza del rivelatore e l’esposizione relativa delle diverse parti del cielo. Per diminuire la probabilità che
la misura sia affetta da fluttuazioni statistiche, il fondo atteso viene ricalcolato un certo numero nof f di volte, dunque α = 1/nof f . Infine bisogna
tenere conto che la significanza è positiva sia nel caso di un eccesso di eventi
rispetto al fondo sia nel caso di un conteggio minore di eventi rispetto al
fondo. Conviene pertanto ridefinirla in modo da distinguere i due casi. Ciò
si può ottenere scambiando nel secondo caso i valori Non e Nof f , sostituendo
ad α il valore reciproco e ponendo la significanza negativa.
3.3
Generazione del fondo isotropo di riferimento
Per poter identificare eventuali eccessi di eventi è necessario effettuare una
stima del numero di conteggi che dovrebbero risultare se la distribuzione degli
eventi fosse perfettamente isotropa. Utilizzando il linguaggio del paragrafo
precedente, è necessario calcolare il valore Nof f da utilizzare per il calcolo
della significanza.
Esistono sostanzialmente due metodi per affrontare questo problema utilizzati all’interno della collaborazione Pierre Auger. Entrambi consistono nel
ricavare l’esposizione in funzione della posizione sulla sfera celeste a partire
dai dati rilevati, essendo estremamente difficoltoso effettuare questo calcolo
a partire da modelli teorici della performance del rivelatore. Si tratta del
metodo
• detto dello shuffling o scrambling. Esso consiste nel generare un campione isotropo di dati ridistribuendo in maniera casuale alcune delle
variabili di ciascun evento in modo da preservare la distribuzione di
altre variabili scelte. Le variabili che possono venire ridistribuite sono
quelle legate al tempo di arrivo del raggio cosmico: tempo UTC, GMT
o JD (Julian day, giorno secondo il calendario giuliano).
• detto semi-analitico. A partire da considerazioni geometriche si approssima l’espressione dell’esposizione in funzione dell’angolo zenitale,
per poi migliorare la stima con un fit polinomiale dei dati a disposizione. Passando dalle coordinate altazimutali a quelle equatoriali si
ottiene l’esposizione finale, ed è possibile correggere per effetti di dipendenza temporale dovuti a modifiche apportate all’array di rivelatori, a
variazioni giornaliere e/o stagionali della temperatura o ad altri effetti.
Infine si generano eventi secondo questa distribuzione.
33
Il rischio nell’utilizzo di entrambi i metodi è che eventuali anisotropie nel
campione di dati iniziale si riflettano nel calcolo del fondo, diminuendo quindi
la sensibilità. Simulazioni Monte Carlo sembrano indicare che in questo senso
il metodo semi-analitico sia migliore rispetto allo shuffling. In questo primo
studio si è però optato per un terzo metodo, ispirato da un precedente lavoro
di R. Bonino [9], che sarà chiamato metodo delle “celle on-off”. Data una
certa cella di nota posizione e raggio angolare sulla sfera celeste (cella “on”)
e un certo intervallo di energia per gli eventi da considerare (e noto quindi
il numero di eventi rilevati nella cella data), il numero di eventi di fondo
viene calcolato considerando sullo stesso campione di dati (ed utilizzando
una stessa soglia energetica) un certo numero nof f di celle di identico raggio
(celle “off”), ma posizionate in parti differenti della sfera celeste, in modo
da non sovrapporsi nè fra di loro nè con la cella on. Il valore di nof f è stato
posto in questo lavoro uguale a 8, mentre le posizioni delle celle off sono
state scelte a declinazione identica a quella della cella on, cosı́ da garantire
la stessa esposizione, che in prima approssimazione (ma piuttosto buona per
dati relativi al solo rivelatore di superficie) è indipendente dall’ascensione
retta.
Figura 3.1: Visualizzazione delle celle on e off in coordinate equatoriali (in
ascisse l’ascensione retta e in ordinate la declinazione in gradi). I punti rossi
sono gli eventi rilevati nella cella on, quelli blu nelle 8 celle off.
3.4
Strategia di scan e ottimizzazione
Definito un parametro di caratterizzazione degli eccessi rispetto al fondo ed
un metodo di stima del fondo stesso, il passo successivo è stato l’iterazione
34
del processo sulla porzione di sfera celeste coperta dal campione di dati. È
stata definita una griglia di punti sulla sfera celeste, separati da un passo di
2◦ sia in ascensione retta che in declinazione. Su ciascuno di questi punti è
stata centrata una cella on di raggio angolare variabile, compreso fra i 2◦ e i
10◦ con un passo di 1◦ . Inoltre sono state considerate soglie minime crescenti
di energia per gli eventi, a partire da 1 EeV fino a 10 EeV con un incremento
di 0.2 EeV. Per ciascuna cella il calcolo della significanza è stato ripetuto per
ogni combinazione di energia e raggio angolare, selezionando la combinazione
di questi parametri che la massimizzasse. La scelta dei passi di incremento
tanto della griglia quanto dei parametri è stata dettata da un compromesso
fra la precisione necessaria nella ricerca e il tempo di computazione richiesto
per completarla. In totale sono stati esaminati circa 104 punti sulla sfera
celeste. Ove necessario lo scan è stato ripetuto su porzioni limitate di cielo
con una griglia più fine (passo 0.5◦ ) in modo da meglio localizzare un eccesso
rivelato dal primo scan. Per poter definire un eccesso come tale è stato infine
imposto che la significanza corrispondente fosse positiva e non inferiore a 4.
3.5
Software e risorse di calcolo
La ricerca è stata implementata attraverso l’esecuzione di alcuni programmi
appositamente scritti a questo scopo. Il linguaggio di programmazione utilizzato è stato il C++, con l’occasionale utilizzo delle librerie di ROOT [33], in
particolare alcuni algoritmi utili per il disegno e il fit di grafici ed istogrammi
e la generazione di numeri casuali.
Visto l’elevato numero di iterazioni del processo di calcolo della significanza (circa 107 ) necessario al completamento della ricerca, essa è stata divisa
su piccole regioni di cielo ed eseguita indipendentemente su diverse macchine
(alcune decine) presso il Laboratorio Calcolo e Multimedia (LCM) del dipartimento di Fisica dell’Università degli Studi di Milano. L’esecuzione di ogni
processo è stata controllata dal software Condor [10], sviluppato precisamente
per l’ottimizazzione delle risorse di calcolo.
Infine i grafici riportanti le posizioni degli eccessi risultanti dalla ricerca
e le posizioni degli oggetti galattici che si è ipotizzato esserne le sorgenti
(si vedano le figure 3.6 4.1 4.1 4.2 4.3 4.4) sono stati generati utilizzando il
framework HEALPix [15].
35
3.6
Risultati
Sono stati individuati sei eccessi di eventi sulla sfera celeste con significanza
superiore a 4. Sono riportate in tabella 3.6 per ogni eccesso le coordinate
equatoriali e galattiche (in gradi), il raggio angolare (in gradi), l’energia
minima (in EeV), il numero di eventi di fondo totali su tutte le celle off, il
numero di eventi di segnale sulla cella on e la significanza. Si noti l’eccesso
numero sei che, nonostante abbia la statistica più bassa, mostra il valore più
alto di significanza ed è localizzato nelle vicinanze del Centro Galattico. Per
una discussione dei risultati si veda il capitolo 4.
Tabella 3.6
Eccesso
1
2
3
4
5
6
RA, Dec
359.5, 20.5
59.5, -60
90.5, 1
124, -16
340, 7
273, -28
l, b
106.3, -40.6
272.3, -44.5
206.3 ,-10.5
237.1, 10.5
75.1, -43.3
3.7, -4.6
36
θ
7
2
6
8
3
2
E Nof f
2.6 354
5.4
51
1.2 4661
2.2 3314
2.4 175
6.2
19
Non
81
21
699
519
47
16
S
4.59921
4.16816
4.38995
4.64595
4.30852
5.15016
Figura 3.2: Eccessi rilevati sulla sfera celeste, in coordinate galattiche. Il
raggio dei cerchi rossi è pari al raggio angolare degli eccessi. La diversa
colorazione del fondo riflette l’esposizione del rivelatore SD dell’Osservatorio
Pierre Auger. La linea blu denota il piano supergalattico
37
38
Capitolo 4
Possibili sorgenti e studio di
correlazione
Sono stati fino a qui descritti i metodi e i risultati relativi ad una cosiddetta
“blind search”, vale a dire una ricerca di eccessi a partire dal solo campione
di dati, senza effettuare un confronto con qualsivoglia oggetto astrofisico. In
questo capitolo viene invece descritto lo studio di correlazione compiuto fra
gli eccessi riscontrati e presentati nel capitolo precedente ed alcuni cataloghi
di corpi celesti che potrebbero soddisfare ai requisiti necessari a fungere da
siti di accelerazione per raggi cosmici.
In base alle considerazioni fatte in precedenza sono stati scelti cataloghi
di soli oggetti presenti all’interno della Galassia, in particolare pulsars, magnetars, stelle binarie a raggi X e un generico catalogo di supernova remnants.
La descrizione dettagliata di ciascuna di queste tipologie di oggetti è presente
nelle sezioni ad esse dedicate (si vedano le sezioni 4.1, 4.2, 4.3, 4.4).
Considerato che sono stati trovati solamente 6 eccessi di eventi mentre
anche il più vasto dei cataloghi presi in esame contiene meno di 300 oggetti,
si è optato per un metodo semplice per la stima della correlazione. Il metodo
consiste nel verificare se ad una data distanza angolare θ da uno qualunque
degli eccessi si trovi almeno un oggetto presente nel catalogo scelto, e contare
il numero di eccessi che soddisfano questa condizione. Sono state considerate
distanze angolari comprese fra 2◦ e 5◦ , con incremento di 1◦ . Il limite inferiore
è dettato dalla bontà della ricostruzione della direzione di arrivo dei raggi
cosmici da parte dell’Osservatorio Pierre Auger a queste energie, mentre il
limite superiore deriva dal considerare che in linea teorica non ci si aspetta
alcuna deflessione dei raggi cosmici nell’ipotesi che siano fotoni o neutroni.
Lasciamo ad un futuro studio l’applicazione di un metodo statisticamente
più elaborato.
39
4.1
X-Ray Binaries
Le stelle binarie a raggi X sono sistemi composti da una stella estesa ed una
stella compatta (una stella di neutroni, una nana bianca o un buco nero). Si
può verificare in questi sistemi il trasferimento di materia dalla stella estesa
a quella compatta, con conseguente formazione di un disco di accrezione intorno a quest’ultima. Il gas che spiraleggia verso la stella compatta emette
energia potenziale gravitazionale sotto forma di radiazione, perciò questi sistemi risultano molto luminosi all’osservazione nei raggi X. Poichè i meccanismi che sottostanno alla produzione di energia nelle stelle binarie a raggi
X sono ritenuti essere sostanzialmente gli stessi che avvengono in AGN, esse
sono ritenute dei plausibili candidati come sorgenti di raggi cosmici.
Le stelle binarie a raggi X vengono usualmente classificate in Low Mass
oppure High Mass a seconda del valore della massa della stella estesa visibile
nell’ottico (non si fa alcun riferimento alla massa della stella compatta). Sono
stati scelti per questo studio due cataloghi, uno di LMXB (186 oggetti)[27]
ed uno di HMXB (114 oggetti)[26].
Figura 4.1: Grafico di correlazione fra eccessi di eventi e LMXB. I primi sono
rappresentati come cerchi rossi, le seconde come stelle nere.
Nel caso delle LMXB un solo eccesso correla a distanze da 2◦ a 5◦ (figura
4.1).
40
Figura 4.2: Grafico di correlazione fra eccessi di eventi e HMXB. I primi sono
rappresentati come cerchi rossi, le seconde come stelle nere.
Anche nel caso delle HMXB un solo eccesso mostra correlazione, ma entro 4◦ , mentre per scale angolari minori non si riscontra alcuna correlazione
(figura 4.1).
4.2
Pulsars
Le pulsars sono stelle di neutroni in rapida rotazione, dotate di un forte
campo magnetico (dell’ordine dei 1012 G). Esse emettono fasci di radiazione
dai poli magnetici, ma poichè non necessariamente l’asse di rotazione e l’asse
magnetico sono allineati, i fasci precessano attorno all’asse di rotazione dando
origine al cosiddetto “effetto faro”.
Le pulsars sono gli oggetti più compatti presenti nell’Hillas plot in grado
di accelerare protoni a 100 EeV. In questo caso i modelli di accelerazione
non utilizzano fronti d’urto e accelerazione stocastica, ma diretta nell’intenso
potenziale elettrostatico presente alla superficie della stella di neutroni.
È stato scelto come catalogo di confronto una lista di pulsars attive nei
raggi gamma, osservate dal satellite Fermi (46 oggetti) [13].
Due eccessi mostrano correlazione su scale angolari di 5◦ , non è stata
riscontrata alcuna correlazione per scale angolari inferiori (figura 4.2).
41
Figura 4.3: Grafico di correlazione fra eccessi di eventi e pulsars individuate
dal satellite Fermi. I primi sono rappresentati come cerchi rossi, le seconde
come stelle nere.
4.3
Magnetars
Le magnetars sono stelle di neutroni dotate di un campo magnetico estremamente intenso, dell’ordine dei 1014 G. Sono in effetti ritenute essere gli oggetti
più fortemente megnetizzati mai osservati, e sono associate alla spiegazione
dei fenomeni detti soft gamma repeaters (SGR) e anomalous X ray pulsars
(AXP). Visto il campo magnetico cosı́ intenso presente in questi oggetti essi
sono un naturale candidato all’accelerazione di particelle.
Il catalogo scelto è stato il McGill [28], contenente 21 oggetti.
Nessuna correlazione fra gli eccessi dalla blind search e magnetars è stata
trovata, a nessuna scala angolare (figura 4.3).
4.4
Supernova Remnants
Supernova remnant è il generico nome con cui si indicano le strutture formatesi a seguito dell’evoluzione di una stella in una supernova. Si tratta di
una vasta gamma di oggetti, spesso di natura composita, ma accomunati dalla formazione di fronti d’urto nella propagazione del materiale espulso dalla
42
Figura 4.4: Grafico di correlazione fra eccessi di eventi e magnetars. I primi
sono rappresentati come cerchi rossi, le seconde come stelle nere.
stella originale durante la fase di supernova attraverso il mezzo interstellare.
A causa di questi fronti esse sono ritenute responsabili dell’accelerazione di
raggi cosmici secondo il meccanismo di Fermi (del primo ordine).
È stato scelto per le SNR il catalogo compilato da D.A. Green [14],
contenente 274 oggetti.
Un solo eccesso correla con le posizioni di SNR entro 2◦ o più, nessuno a
scale minori (figura 4.4).
4.5
Il Centro Galattico
L’eccesso denotato con il numero 6 (si veda la tabella 3.6) è stato trovato
in vicinanza del Centro Galattico. Esso è in effetti localizzato entro 6◦ circa
dal punto della sfera celeste che viene indicato come centro della Galassia ed
entro la stessa scala angolare dal principale oggetto fisico che con esso viene
identificato, Sagittarius A*. Al fine di avere un’indicazione sulla distanza
fisica che separa l’ipotetica sorgente che potrebbe aver prodotto questo eccesso ed il Centro Galattico si può assumere che la distanza dalla Terra tanto
dal Centro Galattico quanto dalla sorgente sia pari a 8 kpc: i due punti disterebbero allora circa 700 pc, vale a dire due volte lo spessore medio del
43
Figura 4.5: Grafico di correlazione fra eccessi di eventi e SNR. I primi sono
rappresentati come cerchi rossi, le seconde come stelle nere.
disco galattico. L’energia minima degli eventi dell’eccesso in questione è pari
a 6.2 EeV. Come si è visto nella sezione 1.4.3 neutroni di tale energia possono propagarsi per oltre 60 kpc prima di decadere, e quindi essere rivelati a
Terra. Al fine di determinare quale sia la probabilità che un eccesso di tale
significanza sia prodotto da una fluttuazione statistica nei dati piuttosto che
da una reale sorgente fisica, il calcolo della significanza è stato ripetuto sulla
stessa area di cielo e stessa energia minima su realizzazioni isotrope dei dati.
Sono stati generati 100 campioni con il metodo dello shuffling e 100 con il
metodo semi-analitico (si veda 3.3). La frazione dei campioni che presentano un eccesso con significanza superiore a quella ottenuta dai dati (5.2 σ)
è risultata in entrambi i casi inferiore all’1 %.
L’ipotetica sorgente di raggi cosmici in questa regione potrebbe essere un
“hot spot” generatosi a partire da attività nel Centro Galattico. Un altro
scenario è rappresentato dalla produzione di fotoni di altissima energia nella
zona del Centro Galattico. In questa regione è relativamente alta la desità
di luce stellare e radiazione infrarossa la cui interazione con UHECR può
produrre fotoni secondari di alta energia [22].
44
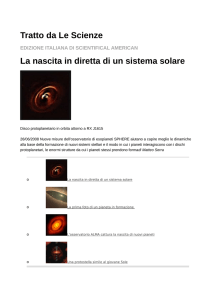
Figura 4.6: Immagine dell’area del Centro Galattico a diverse lunghezze
d’onda: in giallo osservazioni nel vicino infrarosso del telescopio Hubble; in
rosso osservazioni nell’infrarosso dal telescopio Spitzer; in azzurro e viola
osservazioni ai raggi X del telescopio Chandra. L’emissione da Sagittarius
A* è l’area bianco-azzurra in basso a destra. L’immagine copre circa 26
arcominuti o 60 parsec, dunque il punto corrispondente all’eccesso numero 6
non è visibile. Da NASA, ESA, SSC, CXC e STScI.
45
46
Capitolo 5
Conclusioni
La questione scientifica a cui si è tentato di rispodere con questo lavoro è:
da quali oggetti o siti astronomici provengono i raggi cosmici di altissima
energia?
Più precisamente ci si è chiesti se è possibile determinare i siti di accelerazione di raggi cosmici di energia non inferiore ad 1 EeV, nell’ipotesi che
essi siano di origine galattica, utilizzando i dati accumulati dall’ossrvatorio
Pierre Auger. A tale scopo è stata condotta una blind search, vale a dire
una ricerca di eccessi di eventi rivelati rispetto ad una ipotetica distribuzione
perfettamente isotropa. Sono stati riscontrati eccessi rispondenti ai requisiti
imposti, vale a dire sostanzialmente che la loro significanza definita secondo
Li-Ma sia maggiore di 4.
Poichè nel range di energia che si è considerato particelle cariche vengono
ampiamente deflesse dal campo magnetico galattico producendo una distribuzione sostanzialmente isotropa, si è fatta l’ipotesi che gli eccessi trovati
debbano essere dovuti a particelle neutre, in particolare neutroni e fotoni, che
essendo neutri possono puntare direttamente al luogo dal quale sono stati accellerati. Si è dunque proceduto a confrontare le posizioni di questi eccessi
con quelle di alcune categorie di oggetti astronomici comunemente ritenuti
in grado di generare particelle delle energie in gioco, vale a dire gamma ray
pulsars, magnetars, X ray binaries e supernova remnants. Non è stata però
trovata alcuna significativa correlazione con questi oggetti.
Una prima osservazione a tale riguardo riguarda il fatto che dei sei eccessi
trovati, solamente uno è localizzato vicino al piano galattico. Siccome le
possibili sorgenti prese in considerazione sono invece galattiche, è naturale che
si trovi una poco significativa correlazione con esse, o nessuna correlazione.
Invece si è trovata una indicazione di correlazione con il Centro Galattico.
Simili indicazioni sono state riscontrate in precedenti analisi dei dati prodotti
dagli esperimenti AGASA [35] e SUGAR [8], mentre l’analisi effettuata nel
47
2006 su dati raccolti dall’Osservatorio Auger ( prima del completamento del
rivelatore SD) non ha confermato questi risultati [1].
Le incertezze presenti in questi risultati non possono essere eliminate con i
metodi utilizzati in questo primo studio. Esse possono invece essere affrontate
mediante un’ottimizzazione del metodo utilizzato che in particolare preveda:
• un miglioramento della procedura di scansione del cielo, cioè l’ottimizzazione della griglia di ricerca e della scelta degli intervalli di energia e
di scala angolare.
• la discriminzaione della composizione degli eventi, in particolare fra
eventi dovuti a barioni (protoni e nuclei) piuttosto che a fotoni. ciò
è in linea di principio possibile studiando la profondità atmosferica
alla quale lo sciame di particelle giunge al massimo sviluppo; praticamente tale quantità è difficile da determinare, sia dal punto di vista
sperimentale sia a causa delle incertezze sulle sezioni d’urto a queste
energie.
• l’inclusione nello sviluppo della blind search del pattern di deflessione
dei raggi cosmici carichi da parte del campo magnetico galattico. Se
tale pattern non è isotropo si troverebbero eccessi dovuti alla struttura
del campo più che a cluster di sorgenti, col rischio di confondere i
due scenari. Un tale obiettivo non è pero di facile realizzazione viste
le attuali incertezze sia sulla struttura che sull’intensità di tale campo.
Sono interessanti in tal senso studi che guardano al problema dal punto
di vista opposto: cercare di determinare le caratteristiche del campo
dall’effetto che ha sulla deflessione dei raggi cosmici.
• una stima più accurata del fondo generato da una distribuzione perfettamente isotropa delle direzioni d’arrivo dei raggi cosmici. Come
discusso nel capitolo 3, il problema associato a queste stime è il permanere di anisotropie nel fondo quando generato a partire dal campione
di dati stesso, che è anisotropo. Poichè ciò limita fortemente la sensibilità nella rilevazione di eccessi di eventi, è di fondamentale importanza
compiere una stima il più accurata possibile per l’effettuazione di una
blind search.
• la stima della probabilità che gli eccessi trovati siano dovuti a fluttuazioni statistiche nei dati, in modo da poter quantificare l’impatto di
eventuali imprecisioni nel metodo di ricerca sui risultati.
• l’utilizzo di nuovi dati di elevata qualità, che coprano anche la parte
di cielo visibile dal solo emisfero boreale. Risulta in tal senso auspi48
cabile la costruzione del sito nord dell’Osservatorio Pierre Auger, che
attualmente è bloccata per mancanza di fondi.
49
50
Ringraziamenti
Ringrazio il mio relatore Lino Miramonti e la mia corelatrice Viviana Scherini
per l’indispensabile supporto e guida.
Marco Giammarchi e Lorenzo Caccianiga per gli utilissimi suggerimenti
e spunti espressi in innumerevoli discussioni.
Gli amministratori del Laboratorio Calcolo e Multimedia, in particolare
Giorgio Ruffa e Gabriele Vergani, che mi hanno permesso di usufruire della
potenza di calcolo a loro disposizione.
I miei familiari per la pazienza con cui hanno corretto le mie bozze.
51
52
Bibliografia
[1] J. Abraham et al. [Pierre Auger Collaboration], Astropart. Phys. 27
(2007) 244
[2] J. Abraham et al. [Pierre Auger Collaboration], Astropart. Phys. 31
(2009) 399
[3] D. Allard, A. V. Olinto, E. Parizot “On the transition from Galactic
to extra-galactic cosmic-rays: spectral and composition features from
two opposite scenarios” ArXiv Astrophysics e-prints (Dec 2005) astroph/0512345
[4] R. Aloisio, V. Berezinsky, P. Blasi, and S. Ostapchenko “Signatures of
the transition from galactic to extragalactic cosmic rays” ArXiv e-prints
706 (Giu 2007) 0706.2834
[5] P. Auger, P. Ehrenfest, R. Maze, J. Daudin, R.A. Frèon “Extensive
cosmic-ray showers” Rev. Mod. Phys. 11 (Jul, 1939) 288291
[6] L.Bergrstrom, A.Goobar “Cosmology and Particle Astrophysics”
Springer, second edition
[7] P. Bhattacharjee, G. Sigl “Origin and Propagation of Extremely High Energy Cosmic Rays” ArXiv Astrophysics e-prints (1999)
astro-ph/9811011v2
[8] J.A. Bellido et al. Astropart. Phys. 15 (2001) 167 ArXiv:
astro-ph/0009039
[9] R. Bonino, Pierre Auger Collaboration analysis meeting, Lecce (2010);
comunicazione privata (2010)
[10] Condor Project - http://www.cs.wisc.edu/condor/
[11] James W. Cronin “Cosmic rays: the most energetic particles in the
universe” Rev. Mod. Phys. 71 (1999) 165
53
[12] E. Fermi Phys. Rev., 75, 1169 (1949)
[13] Fermi Collaboration, “The First Fermi Large Area Telescope Catalog
of Gamma-ray Pulsars” arXiv:0910.1608v3
[14] D. A. Green “A Catalogue of Galactic Supernova Remnants”
http://www.mrao.cam.ac.uk/surveys/snrs/ e Green D. A., 2009,
Bulletin of the Astronomical Society of India, 37, 45
[15] K. M. Gorski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen,
M. Reinecke and M. Bartelman “HEALPix – a Framework for High
Resolution Discretization, and Fast Analysis of Data Distributed on
the Sphere” Astrophys. J. 622, 759 (2005) [arXiv:astro-ph/0409513]
[16] K. Greisen “End to the cosmic-ray spectrum?” Phys. Rev. Lett. 16
(Apr 1966) 748750
[17] D. Harari, S. Mollerach, E. Roulet “The toes of the ultra high
energy cosmic ray spectrum” ArXiv Astrophysics e-prints (1999)
astro-ph/9906309v2
[18] W. Heitler “Quantum theory of radiation” Oxford University Press
(1944)
[19] V. F. Hess “Uber Beobachtungen der durchdringenden Strahlung bei
sieben Freiballonfahrt” Physikalische Zeitschrift 13 (1912) 1084-1091
[20] A. M. Hillas “Cosmic Rays: Recent Progress and some Current
Questions” ArXiv Astrophysics e-prints (July, 2006) astro-ph/0607109
[21] J. R. Hoerandel “Models of the knee in the energy spectrum of cosmic
rays” Astroparticle Physics 21 (2004) 241
[22] A.Kusenko, J. Schissel, F.W. Stecker “Interactions of ultrahigh-energy
cosmic rays with photons in the galactic center” Astroparticle Physics
25 (2006) 242-245
[23] V. A. Kuzmin, G. T. Zatsepin “Upper limit of the cosmic-ray
spectrum” Zh. Eksp. Teor. Fiz., Pisma Red. 4 (1966), no. 3, 11417
[24] T. Li, Y. Ma “Analysis methods for results in gamma-ray astronomy”,
AsJ 272:317-324, 1 settembre 1983
[25] J.Linsley “Evidence for a primary cosmic-ray particle with energy 1020
eV” Phys. Rev. Lett. 10 (Feb 1963) 146-148
54
[26] Q.Z. Liu, J. van Paradijs, E.P.J. van den Heuvel “Catalogue of highmass X-ray binaries in the Galaxy (4th edition)” arXiv:0707.0549v1
[27] Q.Z. Liu, J. van Paradijs, E.P.J. van den Heuvel “A catalogue of lowmass X-ray binaries in the Galaxy, LMC, and SMC (Fourth edition)”
arXiv:0707.0544v1
[28] McGill Pulsar Group “McGill SGR/AXP Online Catalog”
http://www.physics.mcgill.ca/ pulsar/magnetar/main.html
[29] J. Miralda-Esculdè, E. Waxman “Images of Bursting Sources of HighEnergy Cosmic Rays. I: Effects of Magnetic Fields” ArXiv Astrophysics
e-prints (1996) astro-ph/9607059v1
[30] A. A. Penzias, R. W. Wilson “A measurement of excess antenna
temperature at 4080 mc/s” Astrophys. J. 142 (Lug 1965) 419421
[31] D. Perkins “Particle Astrophysics” Oxford University Press (2004)
[32] Pierre Auger Collaboration, Technical Design Report (2004)
[33] ROOT, a data analysis framework - http://root.cern.ch/
[34] T. Stanev “High Energy Cosmic Rays” Springer, second edition
[35] M. Teshima et al. (AGASA Collaboration), Proceedings of the 27th
ICRC, Hamburg, Vol 1 (2001) 337
55