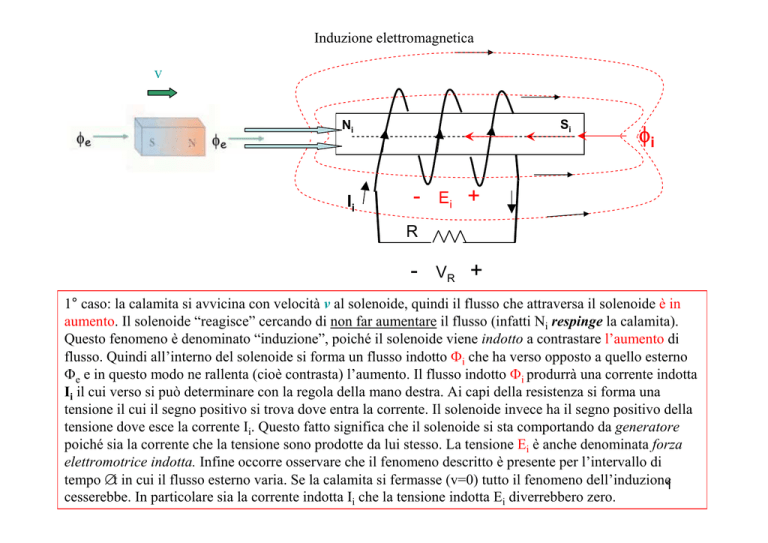
Induzione elettromagnetica
v
Si
Ni
Ii
-
Ei
+
VR
+
φi
R
-
1° caso: la calamita si avvicina con velocità v al solenoide, quindi il flusso che attraversa il solenoide è in
aumento. Il solenoide “reagisce” cercando di non far aumentare il flusso (infatti Ni respinge la calamita).
Questo fenomeno è denominato “induzione”, poiché il solenoide viene indotto a contrastare l’aumento di
flusso. Quindi all’interno del solenoide si forma un flusso indotto Φi che ha verso opposto a quello esterno
Φe e in questo modo ne rallenta (cioè contrasta) l’aumento. Il flusso indotto Φi produrrà una corrente indotta
Ii il cui verso si può determinare con la regola della mano destra. Ai capi della resistenza si forma una
tensione il cui il segno positivo si trova dove entra la corrente. Il solenoide invece ha il segno positivo della
tensione dove esce la corrente Ii. Questo fatto significa che il solenoide si sta comportando da generatore
poiché sia la corrente che la tensione sono prodotte da lui stesso. La tensione Ei è anche denominata forza
elettromotrice indotta. Infine occorre osservare che il fenomeno descritto è presente per l’intervallo di
tempo ∆t in cui il flusso esterno varia. Se la calamita si fermasse (v=0) tutto il fenomeno dell’induzione1
cesserebbe. In particolare sia la corrente indotta Ii che la tensione indotta Ei diverrebbero zero.
v
Si
Ni
Ii
+
Ei
φi
-
R
+
VR
-
2° caso: la calamita si allontana con velocità v dal solenoide, quindi il flusso che attraversa il solenoide è
in diminuzione. Il solenoide “reagisce” cercando di far aumentare il flusso (infatti Si attrae la calamita). Il
solenoide viene indotto a contrastare la diminuzione di flusso. Quindi all’interno del solenoide si forma un
flusso indotto Φi che ha verso concorde a quello esterno Φe e in questo modo ne rallenta (cioè contrasta) la
diminuzione. Il flusso indotto Φi produrrà una corrente indotta Ii il cui verso si può determinare con la
regola della mano destra. Ai capi della resistenza si forma una tensione il cui il segno positivo si trova
dove entra la corrente. Il solenoide invece ha il segno positivo della tensione Ei dove esce la corrente Ii.
Anche in questo caso il solenoide si sta comportando da generatore poiché sia la corrente che la tensione
sono prodotte da lui stesso.
2
v
Ni
Si
+
Ei
-
φi
I
R
I
+
VR
-
v
Si
I
Ni
-
Ei
φi
+
R
-
VR
+
I casi delle figure sono simili a quelli già studiati con la differenza del verso del filo avvolto. In queste3
situazioni la bobina è avvolta in verso opposto.
I fenomeni studiati sono riassunti nella legge di Faraday – Neumann – Lenz che mette in
relazione le seguenti grandezze fisiche:
1) Variazione di flusso ∆Φ;
2) Intervallo di tempo ∆t in cui varia il flusso;
3) Tensione indotta Ei
∆Φ
Ei = −
∆t
Il segno “-” presente nell’equazione non ha un significato matematico bensì fisico: esso tiene conto del
fenomeno dell’induzione e cioè che la tensione indotta Ei si oppone alla variazione del flusso Φ.
Una seconda osservazione importante deriva dal denominatore ∆t. Se l’intervallo nel quale varia il flusso è
piccolo significa che esso varia rapidamente e cioè che la velocità con la quale si muove la calamita è
grande. Di conseguenza un ∆t piccolo produce una grande tensione indotta Ei (infatti sono inversamente
proporzionali). Al contrario se l’intervallo in cui varia il flusso è grande la tensione indotta è piccola.
Tutto ciò ha un significato energetico importante: una velocità grande (∆t piccolo) implica una grande
energia cinetica della calamita 1 2
mv
2
Questo spiega perché la tensione indotta Ei è grande poiché l’energia cinetica si trasforma in energia
elettrica W utilizzata dalla resistenza:
Welettrica = P ⋅ ∆t = Ei ⋅ I i ⋅ ∆t
4
Autoinduzione
φc
I = cost
I
VL=0
I = cost
+ U
R
I = cost
t
CASO A)
Alimentiamo con una tensione continua U un solenoide e una resistenza. Tale tensione produce una
corrente costante la quale produce un flusso concatenato ΦC costante all’interno del solenoide. Non
avendo una variazione di flusso non si avrà neanche il fenomeno dell’induzione elettromagnetica.
Quindi la tensione ai capi del solenoide VL = 0.
La conseguenza è la seguente: in condizioni di correnti continue il solenoide si comporta come se fosse
un corto circuito poiché si lascia attraversare dalla corrente senza opporre “impedimenti” e senza
assorbire alcuna tensione.
5
φc +∆φ
∆φ
φi
Ii
+
I + ∆I
U+∆U
+
-
VL
R
Ii I
I + ∆I
I
CASO B)
∆t
t
Supponiamo ora di aumentare la tensione del generatore portandola gradualmente in un intervallo di tempo
∆t dal valore U ad un valore maggiore U+∆U. Anche la corrente aumenterà nello stesso tempo dal valore I
fino al valore I+∆I. Come conseguenza dell’aumento della corrente si avrà un aumento di flusso che varierà
dal valore iniziale ΦC al valore ΦC + ∆Φ.
A questo punto il solenoide reagisce secondo il principio dell’induzione elettromagnetica “opponendosi”
all’aumento di corrente e di flusso. Il flusso indotto e la corrente indotta quindi avranno i versi indicati in blu.
Il verso della corrente indotta Ii si ottiene usando la regola della mano destra applicata al flusso indotto Φi.
Si nota che il solenoide si comporta come un generatore presentando ai suoi capi una tensione VL (la tensione
indotta Ei ) con polarità tali da “spingere” la corrente indotta Ii in verso opposto a quella proveniente dal
generatore U.
6
φc -∆φ
∆φ
φi
Ii
-
I - ∆I
U-∆U
+
VL +
R
I
Ii
I
I - ∆I
∆t
t
CASO C)
Supponiamo ora di diminuire la tensione del generatore portandola gradualmente in un intervallo di tempo ∆t
dal valore U ad un valore minore U-∆U. Anche la corrente diminuirà nello stesso tempo dal valore I fino al
valore I-∆I. Come conseguenza dell’aumento della corrente si avrà una diminuzione di flusso che varierà dal
valore iniziale ΦC al valore ΦC - ∆Φ.
A questo punto il solenoide reagisce secondo il principio dell’induzione elettromagnetica “opponendosi” alla
diminuzione di corrente e di flusso. Il flusso indotto e la corrente indotta quindi avranno i versi indicati in
blu. Il verso della corrente indotta Ii si ottiene usando la regola della mano destra applicata al flusso indotto
Φi.
Si nota che il solenoide si comporta come un generatore presentando ai suoi capi una tensione VL (la tensione
indotta Ei ) con polarità tali da “spingere” la corrente indotta Ii in verso concorde a quella proveniente dal
7
generatore U.
φc
VL=0
I = cost
I = cost
+ U
R
I
I = cost
t
Il caso disegnato si differenzia da quello studiato al caso A) per l’avvolgimento della bobina che è
realizzato in verso opposto. Tuttavia siccome non c’è variazione di flusso anche la tensione indotta è
zero, come nel caso A).
8
φc +∆φ
∆φ
φi
Ii
+
I + ∆I
U+∆U
-
VL
Ii
R
+
I
I + ∆I
I
∆t
t
Il caso disegnato si differenzia da quello studiato al caso B) per l’avvolgimento della bobina che è
realizzato in verso opposto. Anche adesso c’è una variazione di flusso in aumento e quindi è presente
una tensione indotta come nel caso B). Da notare che le polarità della tensione indotta VL sono
identiche a quelle del caso B).
9
φi
φc -∆φ
∆φ
Ii
I - ∆I
U-∆U
+
I
+
VL
R
Ii
I
I - ∆I
∆t
t
Il caso disegnato si differenzia da quello studiato al caso C) per l’avvolgimento della bobina che è
realizzato in verso opposto. Anche adesso c’è una variazione di flusso in diminuzione e quindi è
presente una tensione indotta come nel caso C). Da notare che le polarità della tensione indotta VL
sono identiche a quelle del caso C).
10
La discussione fatta si può riassumere con le seguenti conclusioni:
1) Non è importante il verso dell’avvolgimento della bobina poiché la tensione indotta ha lo stesso verso in
entrambi i casi;
2) Quando c’è un aumento flusso (cioè quando la corrente aumenta, fig. a) la tensione indotta VL ha un
verso che genera un flusso indotto che si oppone all’aumento del flusso esterno (cioè si sottrae ad esso,
poiché è discorde).
3) Quando c’è una diminuzione flusso (cioè quando la corrente diminuisce, fig. b) la tensione indotta VL ha
un verso che genera un flusso indotto che si oppone alla diminuzione del flusso esterno (cioè si somma
ad esso, poiché è concorde).
4) Convenzione sul verso della tensione indotta VL:
a) Il verso è negativo se il flusso indotto è discorde con il flusso esterno;
b) Il verso è positivo se il flusso indotto è concorde con il flusso esterno.
5) La tensione indotta VL si calcola con la legge di Lenz di pagina 4
V
V
L
L
∆Φ
VL = Ei = −
∆t
11
Per poter applicare le leggi Kirchoff e di Ohm ad un circuito come quello indicati nelle figure a) e b)
occorre esprimere la legge di Lenz con le correnti e non con il flusso.
Ricordando la legge di Hopkinson si possono ottenere le seguenti relazioni:
ℜ ⋅ Φ = N ⋅ I;
Φ C = N ⋅ Φ;
N2
L=
;
ℜ
N ⋅I
Φ=
ℜ
N2 ⋅ I
ΦC =
ℜ
Il flusso ΦC è denominato flusso
concatenato, ed è il flusso che attraversa una
sola spira, la quale è percorsa dalla stessa
corrente I che percorreva le N spire
concatenate con un flusso Φ.
La grandezza L è denominata autoinduttanza
o induttanza L.
ΦC = L ⋅ I
Dall’ultima relazione si ricava:
ΦC = L ⋅ I ;
∆Φ C = Φ C ( finale ) − Φ C (iniziale )
∆I = I finale − I iniziale
∆Φ C = L ⋅ ∆I
∆Φ C
∆I
VL = −
= −L ⋅
∆t
∆t
12
Questa è la formula che ci permette di studiare i circuiti che presentano delle bobine o solenoidi e che d’ora
in avanti chiameremo circuiti induttivi, poiché sono identificabili dalla grandezza autoinduttanza o
semplicemente induttanza L.
C
L
∆Φ
∆I
V =−
= −L ⋅
∆t
∆t
Considerando che il solenoide si comporta come un generatore si può scrivere la seguente legge di
Ohm: Ug + VL = R*i
Possiamo sostituire alla tensione indotta VL la formula trovata e si avrà:
∆I
Ug = R ⋅i + L ⋅
∆t
Questa ultima formula si comprende nel seguente modo:
Se nel circuito induttivo si vuole aumentare la corrente i
(fig. a) dove ∆I è positivo) occorre aggiungere alla
∆I per vincere
tensione del generatore Ug la tensione
L⋅
la f.e.m. di autoinduzione.
∆t
∆I
Ug − L ⋅
= R ⋅i
∆t
i=
= Ug
VL
13
i=
Al contrario se si vuole diminuire la corrente i (fig. b) dove ∆I è negativo,
cioè diminuisce I) occorre sottrarre alla tensione del generatore Ug la
∆I per vincere la f.e.m. di autoinduzione
tensione
L⋅
= Ug
∆t
VL
Quindi per quanto riguarda la tensione applicata del generatore si può dire che essa deve vincere non solo
le cadute di tensione ohmiche rappresentate dal termine R*i, ma anche le cadute induttive rappresentate
dal termine L ⋅ ∆I Queste tensione aggiuntiva come già detto occorre per vincere le f.e.m. di
∆t
autoinduzione che si oppongono alle variazioni di corrente. Questa caduta induttiva si somma alla caduta
ohmica quando la corrente aumenta (fig a) e si sottrae quando la corrente diminuisce (fig. b).
Essa quindi rappresenta una tensione addizionale che occorre per accelerare la corrente quando essa deve
aumentare, oppure una controtensione che occorre per frenarla quando essa deve diminuire, in modo
simile a quando si vuole accelerare o frenare un corpo in moto.
14
FENOMENI TRANSITORI
Da quanto detto nelle pagine precedenti si ricava che i fenomeni d’induzione sono di tipo inerziale ed ora
possiamo anche comprendere ciò che accade quando si chiude o si apre velocemente un circuito induttivo.
Consideriamo come esempio un circuito formato da un solenoide d’induttanza L in serie ad una resistenza
R al quale si applichi istantaneamente una tensione di valore costante Ug.
S
L’equazione che descrive il circuito è quella già trovata in precedenza e
riportata di seguito.
i
Ug = R ⋅i + L ⋅
Ug
VL
∆I
∆t
Nell’istante iniziale in cui si chiude l’interruttore S la tensione Ug si
applica interamente al circuito. La corrente tende ad aumentare ma è
contrastata dall’induttanza del solenoide che si oppone al suo
aumento tramite una f.e.m. di autoinduzione. Quindi all’istante
iniziale siccome la corrente è zero anche la tensione ai capi della
resistenza è zero. Da ciò deriva che la tensione del generatore si
applica tutta ai capi del solenoide, il quale cioè si comporta come un
circuito aperto.
t = 0 >>> i = 0 >>> VR = R*i =0 >>> U g = L ⋅
∆I
∆t
Questo comportamento è usato nella protezione di elettrodomestici delicati nei confronti di sovratensioni
provocate da fulmini.
15
Al passare del tempo tuttavia la corrente inizia a scorrere per gradi e dopo un tempo teoricamente infinito
raggiunge il suo valore massimo. Questo valore massimo è ovviamente costante e quindi il solenoide non si
oppone al suo passaggio. Quindi dopo un tempo praticamente molto lungo la tensione VL (caduta induttiva)
si annulla, ciò significa che il solenoide si sta comportando come un corto circuito. Ovviamente la tensione
del generatore si applica interamente alla resistenza e la corrente quindi vale I = Ug / R. Il tempo per
raggiungere il massimo si può approssimare a circa 5 volte una costante di tempo τ che si dimostra valere
L / R.
i
Ug
I= Ug /R
t
α
tan α =
R
⋅I
L
t
Dal fatto che τ = L/R si deduce che per avere tempi lunghi occorre aumentare L e diminuire R,
mentre per avere tempi brevi occorre diminuire L ed aumentare R.
Ora consideriamo lo stesso circuito nel quale sia presente la corrente costante appena trovata e
immaginiamo eliminare il generatore e istantaneamente sostituirlo con un filo.
16
In questo circuito non esistendo più il generatore, la corrente tende ad
annullarsi, ma in ciò è contrastata dalla f.e.m. indotta del solenoide. Quindi
la sua diminuzione procede per gradi, più o meno lentamente a seconda della
costante di tempo τ = L / R.
I
t
Il meccanismo fisico descritto si può paragonare ad un volano abbandonato a sé stesso e che
continua a girare sempre meno velocemente fino a fermarsi. Tuttavia è anche impensabile bloccare
immediatamente la sua rotazione ed è anche altrettanto impensabile azzerare la corrente
istantaneamente.
Infatti se si cerca di aprire l’interruttore S del circuito
i
precedente si forma una elevata f.e.m. indotta tale da
Ug
innescare un arco elettrico tra i contatti dell’interruttore
stesso. L’arco elettrico si produce quando l’aria
VL (normalmente isolante) viene sottoposta ad una tensione
abbastanza elevata (20 ÷30 kV/cm) che la ionizza e
quindi la rende conduttiva. In tal modo il circuito
continua a condurre e si può andare incontro alla
17
distruzione dell’interruttore e delle apparecchiature.












