Le Righe di Emissione di un AGN

Nuclei Galattici Attivi
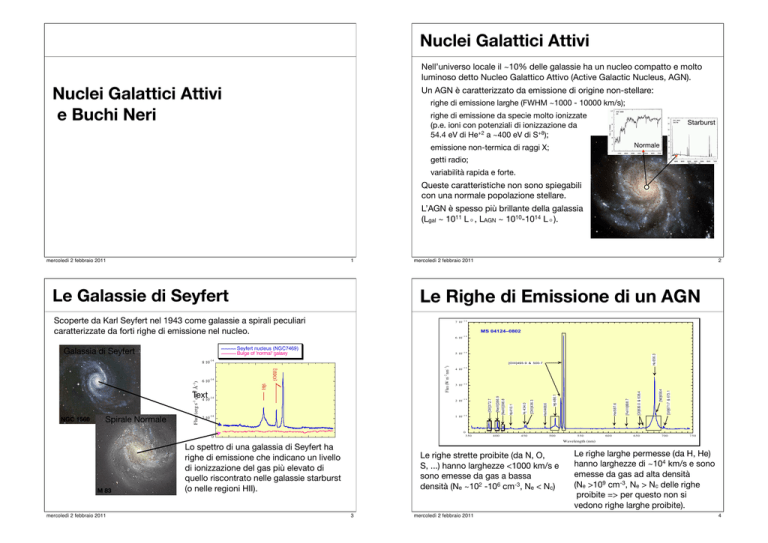
Nell’universo locale il ~10% delle galassie ha un nucleo compatto e molto
luminoso detto Nucleo Galattico Attivo (Active Galactic Nucleus, AGN).
Nuclei Galattici Attivi
e Buchi Neri
Un AGN è caratterizzato da emissione di origine non-stellare:
righe di emissione larghe (FWHM ~1000 - 10000 km/s);
righe di emissione da specie molto ionizzate
(p.e. ioni con potenziali di ionizzazione da
54.4 eV di He+2 a ~400 eV di S+8);
Starburst
Normale
emissione non-termica di raggi X;
getti radio;
variabilità rapida e forte.
Queste caratteristiche non sono spiegabili
con una normale popolazione stellare.
L’AGN è spesso più brillante della galassia
(Lgal ~!1011 L , LAGN ~!1010-1014 L ).
mercoledì 2 febbraio 2011
1
Le Galassie di Seyfert
mercoledì 2 febbraio 2011
Le Righe di Emissione di un AGN
Scoperte da Karl Seyfert nel 1943 come galassie a spirali peculiari
caratterizzate da forti righe di emissione nel nucleo.
7 10
-16
6 10
-16
5 10
-16
4 10
-16
3 10
-16
2 10
-16
1 10
-16
0
350
0
M 83
mercoledì 2 febbraio 2011
400
500
550
600
650
[SII]671.7 & 673.1
[OI]630.0 & 636.4
[FeVII]608.7
HeI587.6
H# 486.1
[OIII]436.3
H" 434.0
450
HeII468.6
2 10-14
[OII]372.7
Flux (W m- 2 nm- 1)
[OIII]
-14
[NeIII]386.9
[NeIII]396.8
Spirale Normale
H!
Flux (erg s-1 cm-2 Å-1 )
6 10-14
Text
4 10
NGC 1566
[OIII]495.9 & 500.7
[NII]658.4
Seyfert nucleus (NGC7469)
Bulge of 'normal' galaxy
8 10-14
H$ 656.3
MS 04124–0802
H!410.1
Galassia di Seyfert
2
700
750
Wavelength (nm)
Lo spettro di una galassia di Seyfert ha
righe di emissione che indicano un livello
di ionizzazione del gas più elevato di
quello riscontrato nelle galassie starburst
(o nelle regioni HII).
Le righe strette proibite (da N, O,
S, ...) hanno larghezze <1000 km/s e
sono emesse da gas a bassa
densità (Ne ~102 -106 cm-3, Ne < Nc)
3
mercoledì 2 febbraio 2011
Le righe larghe permesse (da H, He)
hanno larghezze di ~104 km/s e sono
emesse da gas ad alta densità
(Ne >109 cm-3, Ne > Nc delle righe
proibite => per questo non si
vedono righe larghe proibite).
4
Galassie di Seyfert: AGN a bassa L
I Quasar
Esistono due tipi di galassie di Seyfert in base alla presenza o meno di righe
larghe nello spettro:
broad → ~ 5000 km/s (> 1000 km/s)
Simili alle Seyfert 1 ma molto più luminosi (L > 4"1045 erg s-1 = 1012 L ) e si
trovano a redshift (→distanze) più elevate.
Sono più luminosi delle galassie più
luminose note.
La loro luminosità “nasconde” la
galassia ospite ed hanno un’apparenza
stellare
(Quasar = quasi stellar object).
Seyfert 1 (Sy1)
righe larghe (broad)
permesse (Hα, Hβ, HeII etc.);
~20%
di tutte le
Seyfert
[OII]
continuo UV-X forte e variabile;
le righe permesse sono
strette (narrow);
[NII]
[OIII]
HeII
Fλ
luminosità fino a ~1045 erg/s (~2"1011
L ).
Seyfert 2 (Sy2)
narrow → ~ 500 km/s (< 1000 km/s)
Hα
Hβ
~80%
di tutte le
Seyfert
[OI]
[SII]
3C 273 - il quasar più vicino
e la sua galassia ospite.
Lunghezza d’onda (Å)
continuo UV-X molto debole rispetto
a quello stellare della galassia ospite.
Broad Line Region (BLR): regione
compatta, di alta densità (n >109 cm-3)
Narrow Line Region (NLR): regione estesa
di bassa densità (n ~102 -106 cm-3)
mercoledì 2 febbraio 2011
Spettro tipico di un quasar.
5
I Quasar
La magnitudine assoluta è M = -26.2
Per una galassia brillante M " -21.
Centauro A
(NGC 5128)
3C 273
Lobi di emissione radio
Fe II
[OIII]
Flux (erg s-1 cm-2 Å-1 )
3 10-14
Fe II + He II
H!
Redshift z = (!-!0)/!0 = 0.158
Il modulo di distanza è
m-M = 5 log( d[Mpc] ) +25
Alcuni nuclei attivi sono caratterizzati da una forte emissione radio anche
estesa su dimensioni molto più grandi della galassia stessa (>100 kpc).
4 10-14
Esempio di 3C 273:
La magnitudine apparente è m=13
6
Gli AGN radio-loud
Dato il redshift “elevato” dei quasar più vicini (z~0.1) inizialmente non si
riusciva a capire cosa fossero le righe osservate negli spettri di queste “stelle”
Dalla legge di Hubble la distanza in
Mpc è
d = cz/H0 = 677 Mpc
mercoledì 2 febbraio 2011
2 10-14
X+Ottico+Radio
H#
1 10-14
0
450
"0 = 486.1 nm
rest
500
" = 562.8 nm
observed
550
600
650
Anche i Quasar possono avere una forte
emissione radio: Quasar Radio Loud.
Hanno L più elevate delle radio galassie.
Wavelength (nm)
3C 273 è ~100 volte più brillante di una galassia brillante ed ha L~1012 L .
La radio
galassia
Fornax A
Galassia Ellittica
L’ emissione radio e’ di sincrotrone da elettroni relativistici
mercoledì 2 febbraio 2011
7
mercoledì 2 febbraio 2011
8
Getti relativistici
Getti relativistici
Cygnus A
Gli AGN radio-loud sono caratterizzati da getti di materiale molto collimati
che partono dal nucleo e terminano nei lobi radio.
Questi getti sono osservati nel radio, ma anche nell’ottico e nell’X.
Spesso i blob lungo il getto si muovono di moto superluminale ovvero con
velocità
apparenti > c (→ moti relativistici in direzione
vicina alla
linea di vista).
M87: HST (ottico)
NGC 6251
mercoledì 2 febbraio 2011
9
mercoledì 2 febbraio 2011
10
BL Lac
Distribuzione Spettrale di Energia
Alcuni AGN sono peculiari nel senso che sono caratterizzati da:
sorgenti radio compatte (no lobi) e molto potenti;
Combinando le informazioni fotometriche nelle varie bande dello spettro e.m.
è possibile ricostruire la distribuzione spettrale di energia (Spectral Energy
Distribution, SED) di un AGN.
spesso “blob” di emissione radio mostrano moti superluminali (velocità
apparenti sul piano del
cielo > c);
hanno spettri dominati da
continuo fortemente
polarizzato privo di righe di
emissione;
L’integrale della SED fornisce la luminosità totale (bolometrica) dell’AGN.
La SED è rappresentata spesso da un grafico log νFν - log ν (se asse x è log
ν, log νFν è direttamente legata all’area sotto la curva ovvero all’integrale).
Si osservano varie componenti:
Big Blue Blump, IR Bump, raggi X.
La caratteristica principale è che
log νFν # costante dal radio ai
raggi X.
sono estramamente variabili
in luminosità.
La potenza radio è una
eccezione: solo il 10% degli
AGN sono radio-loud
Questi AGN sono detti:
BL Lac
Radio
Loud
11
mercoledì 2 febbraio 2011
IR bump
Big Blue
Bump
0
X-rays
-1
Radio
Quiet
12
Gli Optically Violently Variable (OVV) Quasars sono simili ai BL Lac ma presentano
righe di emissione; assieme ai BL Lac costituiscono la classe di Blazars
mercoledì 2 febbraio 2011
log ν
F(ν)
la SED è più piatta di quella
degli altri AGN;
Spectral Energy Distribution (SED)
14
log ν
16
18
20
12
Emissione non-stellare
Gli spettri di galassie normali sono
dominati da emissione termica di corpo
nero in due bande:
Spettri di AGN
Galassie di Seyfert
3C 273 (Quasar radio loud)
Blazar
(radio-loud)
Visibile/Vicino IR: stelle;
Lontano IR: polvere riscaldata dalle stelle
Quasar
Spectral Energy Distribution (SED)
F(ν)
log ν
Big Blue
Bump
IR bump
0
Radio Galassie
Radio
Loud
AGN debole
X-rays
-1 Radio
Quiet
O star
Warm/hot
dust
12
14
log ν
Galassia Normale
16
18
20
Galassia a spirale
mercoledì 2 febbraio 2011
13
Principali Classi di AGN
mercoledì 2 febbraio 2011
14
Variabilità
Curva di luce nel visibile del blazar 3C279
L’emissione delle galassie normali
è dovuta a ~1011 stelle
→ la luminosità non varia.
mercoledì 2 febbraio 2011
15
mercoledì 2 febbraio 2011
La luminosità di un AGN è
variabile a tutte le lunghezza
d’onda con tempi scala di ~ore
(raggi X) - mesi (visibile/IR).
I Blazar sono gli AGN più variabili.
16
Il Motore Centrale?
Dimensioni del “Motore” centrale
Qual’è la sorgente di energia degli AGN?
Il meccanismo fisico di produzione dell’energia deve rispettare le seguenti
caratteristiche osservative:
Spettri non-stellari (SED, continuo e righe di emissione; forte emissione UV, X e
radio);
Rapida variabilità (in alcuni casi < ore) ovvero sorgente compatta;
La variabilità determina un
limite superiore alle dimensioni
della regione emittente:
Sorgenti radio estremamente compatte (p.e. Centauro A < 10 lt-days);
Moti superluminali (accelerazione di plasma a velocità relativistiche);
R $ c Δt
R dimensioni della regione emittente, Δt tempo scala di variabilità
Getti collimati in direzione ben definita anche su lunghezze fino a Mpc (direzione
fissata → ottimi giroscopi);
La rapida variabilità X in una galassia di Seyfert è caratterizzata da un
tempo scala Δt~104 s ovvero R $ 3"1012 m (20 AU).
mercoledì 2 febbraio 2011
17
mercoledì 2 febbraio 2011
18
Efficienza di conversione M-E
Il Motore Centrale
Le reazioni di fusione nucleare hanno efficienza “bassa”.
Esempio: catena p-p nel Sole ovvero 4 1H → 4He + 2γ+2νe
massa iniziale: 4 " mp = 4 "1.0078 amu = 4.0312 amu
(atomic mass unit, amu = 1.66x10-27 kg)
massa finale (nucleo 4He) = 4.0026 amu
massa convertita in energia: Δm = 0.0286 amu
Efficienza di conversione: ϵ = Δm/4mp = 0.0286/4.0312 = 0.007 = 0.7%
Tempo scala di variabilità di ~3 ore → dimensioni d ~!c Δt = 10-4 pc
Supponiamo che la sorgente sia costituita da stelle con massa totale M e che
“brucino” una frazione f della massa totale nel tempo Δt con efficienza ε:
L’unico processo che può fornire una alta efficienza di conversione M-E in
volumi piccoli è l’accrescimento su un oggetto compatto.
L’efficienza massima si avrà per l’oggetto più compatto noto ovvero un
Buco Nero
Il gas interstellare possiede momento angolare e si dispone a formare un
disco di accrescimento ruotante attorno al buco nero.
Nel disco, la viscosità permette al gas di perdere momento angolare e quindi
di cadere verso il BH, convertendo energia gravitazionale in radiazione
elettromagnetica e producendo particelle accelerate a velocità relativistiche.
E potenziale gravitazionale → E
cinetica del gas → Calore
(tramite la viscosità) →
radiazione EM (corpo nero).
2
ε f M� c
L=
∆t
con i valori ε=0.7%, f=10% e Δt = 107 y (molto conservativi) si ottiene che per
avere L = 1045 erg/s si devono avere stelle per M ~108 M in 10-4 pc ovvero ρ
~1020 M pc-3 ... impossibile (→ centro Galattico).
mercoledì 2 febbraio 2011
magnetic fields &
relativistic particles
Accretion disk
Black hole
X-ray & UV radiation
19
mercoledì 2 febbraio 2011
20
La Produzione di Energia
La Produzione di Energia
Relatività generale: l’orbita stabile più interna di un disco di accrescimento
attorno ad un BH (non ruotante) ha raggio R0 = 3 RS (Raggio di
Schwarzschild).
Dal Teorema del Viriale 1/2 ΔU è irraggiata per cui l’energia irraggiata è:
Qual’è l’efficienza di conversione di materia in energia?
L’efficienza di irraggiamento è ε = 1/12 mc2 / mc2 = 1/12 = 0.083
Una frazione non trascurabile (~10%) dell’energia a riposo (E=mc2) è
irraggiata nel processo di accrescimento (reazioni di fusione nucleare nelle
stelle hanno ε = 0.7%)
E=
Dobbiamo calcolare l’energia potenziale gravitazionale rilasciata da una
particella di massa m che passa da distanza infinita a R0.
MBH
U3RS
GMBH m
=−
3Rs
r = ∞ → U∞ = 0
∆U3RS = U∞ − U3RS =
m
21
La Produzione di Energia
BH non ruotante
(Schwarschild)
3 RS
BH massimamente
ruotante (Kerr)
0.5 - 4.5 RS
con RS =
2GMBH
c2
mercoledì 2 febbraio 2011
22
Il disco di accrescimento
Conservazione del momento angolare -> disco di accrescimento
Da calcoli più accurati che tengono anche conto del processi di
accrescimento nel disco si ottiene
Orbita stabile più
interna
1
mc2
12
La luminosità tipica di un quasar è
L ~ 1046 erg/s con ε ~!0.1.
Massa m rilascia energia E = ε mc2 per cui
la luminosità è L = ΔE/Δt = ε c2 Δm/Δt
e Δm/Δt è il tasso di accrescimento (M /yr) necessario.
Per L = 1046 erg/s, con ε ~!0.1 si ottiene Δm/Δt ~ 0.2 M /yr
GMBH m
3RS
mercoledì 2 febbraio 2011
E=
Quanta massa deve essere accresciuta per
anno per emettere le luminosità osservate?
3RS
La variazione di energia potenziale è:
∆U3RS
GMBH m
=
2
6RS
Per avere accrescimento bisogna
che il disco trasporti verso l’esterno
il momento angolare del gas
Efficienza
conversione M→E
Il modello piu’ semplice e’ quello
del cosidetto α-disk in cui il traferimento
di momento angolare avviene tramite
viscosita’ dovuta ai moti turbolenti
0,057
La torsione sul gas e’ data da
0.3 - 0.42
mom.
ang.
Torque
se moto Kepleriano
e densita’ ~costante
Torque = ρ ν R %&/%R ! R-1.5
densita’ viscosita’ velocita’ differenziale
fra i diversi anelli
Quindi le parti piu’ interne sono quelle in cui la torsione e’ maggiore,
dove la conversione di energia gravitazionale e’ piu’ rapida
-> dove si ha un riscaldamento maggiore
mercoledì 2 febbraio 2011
23
mercoledì 2 febbraio 2011
24
Il disco di accrescimento
Il disco di accrescimento
le parti piu’ interne irradiano a λ piu’ corte
Si ottiene che T ! R-3/4
Disco a due fasi
i BH ruotanti possono essere piu’ caldi
corona calda 109 K
disco “freddo” 105 K
Integrando l’emissione termica
di tutti gli anelli del disco si
ottiene lo spettro complessivo
Gli elettroni caldi della corona del disco
interagiscono per scattering Compton inverso
con i fotoni del disco spostandone l’energia
nei raggi-X
disco freddo
Lo spettro risultante e’
molto vicino a quello del
Big Blue Bump osservato
comptonizzazione
Problema: manca l’emissione X !
mercoledì 2 febbraio 2011
25
Il limite di Eddington è il limite superiore della luminosità che può essere
prodotta dall’accrescimento gravitazionale.
E’ la massima luminosita’ che puo’ essere emessa per accrescimento:
a questa luminosita’ la forza esercitata dalla pressione di radiazione e’
uguale alla forza gravitazionale
FR
FG = G
L
4'R2
mH MBH
c
Forza di pressione di
radiazione sugli elettroni
(che si trascinano il protoni)
σT
26
Il Limite di Eddington
La luminosita’ di Eddington
FR = PR σT =
mercoledì 2 febbraio 2011
E’ determinato dall’equilibrio tra la forza gravitazionale e la
pressione di radiazione sul gas in accrescimento (forza
gravitazionale su protone, pressione di
radiazione su elettrone).
FG
Anche se il gas e’ ionizzato,
nel plasma elettroni e protoni
sono accoppiati per interazione
columbiana
Forza gravitazionale
R2
Pressione di
radiazione
Attrazione
gravitazionale
Se la luminosità eccede il limite di Eddington,
l’accrescimento è bloccato dalla pressione di radiazione.
In un oggetto di massa M che irraggia (p.e. stella, BH) il limite di Eddington è
Si ha accrescimento se FG > FR
Massa della sorgente (BH)
L < LE =
Ovvero se
Flusso =
L
4'R2
p = E/c
4! c G mp MBH
σT
PR =
4πGc mp
LE =
MBH
σe
= 1.3 x 1038 MBH erg/s
Msun
Sezione d’urto Thomson (diffusione
radiazione da parte dell’elettrone)
L
4'R2c
LE ≈ 3 × 104
�
M
M⊙
�
L⊙
Massa del protone
pressione di radiazione
mercoledì 2 febbraio 2011
27
mercoledì 2 febbraio 2011
28
Perchè un BH molto massiccio?
La Broad Line Region (BLR)
Quanto massiccio deve essere un buco nero per irraggiare con la luminosità
di un AGN?
Se richiediamo che che LAGN < LEdd (limite di Eddington) allora si ottiene:
�
�
�
�
L
4πGc mp
M
−5
4
MBH ≥ 3 × 10
M⊙
LE =
ML
L⊙
BH
E ≈ 3 × 10
L⊙
σe
M⊙
La Broad Line Region è costituita da nubi di gas denso (NH~109-1013 cm-3),
fotoionizzate dalla sorgente centrale e “fredde”, Te~2"104 K).
Le variazioni nell’emissione della radiazione continua ionizzante emessa dal
disco di accrescimento sono seguite da “echi” nelle righe larghe che però
hanno un ritardo τ.
Il ritardo è “light travel time” ovvero il tempo necessario alla propagazione
della radiazione ionizzante e dei fotoni della riga: Δτ ~ r / c
La misura del ritardo Δτ fornisce quindi una stima delle dimensioni della
regione delle righe larghe.
1
Δτ1 = r / c
Δτ
LAGN (L )
MBH (M )
Galassia di Seyfert tipica
3"1010
( 106
Quasar tipico
3"1012
( 108
Quasar luminosi
1"1015
( 3x1010
Flusso
Riga
Il limite di Eddington può essere violato se l’accrescimento avviene nel piano
equatoriale (disco) e la radiazione viene emessa principalmente lungo l’asse
polare (perpendicolare al disco).
mercoledì 2 febbraio 2011
Nube
di gas
Continuo
Tempo
29
mercoledì 2 febbraio 2011
4
r
2
Nucleo del
Quasar
3
Δτ2 = 0
Δτ4 = 2r / c
Δτmean
~r/c
Δτ3 = r / c
30