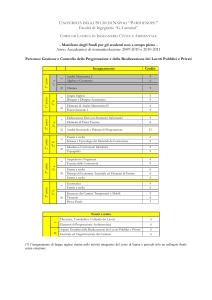
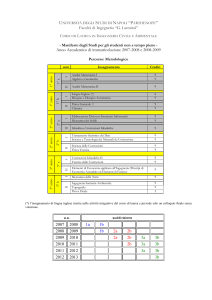
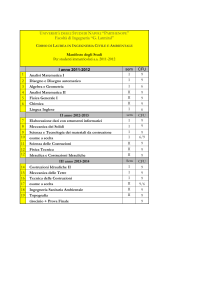
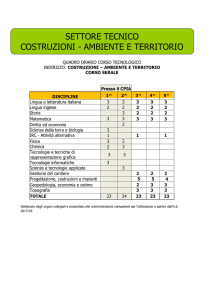
Richiami di calcolo
delle p
probabilità
probabilità
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
1
Riferimenti bibliografici
g
1. G. Vicario, R. Levi “Calcolo delle probabilità e
statistica per ingegneri”, Progetto Leonardo
2 S
2.
S. Bernstein,
Bernstein R
R. Bernstein “Calcolo
Calcolo delle probabilità
probabilità”,
Mc Graw-Hill
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
2
Perché parlare di probabilità?
Gli EVENTI che si verificano quotidianamente non
sono prevedibili con CERTEZZA.
Esempi:
- condizioni meteorologiche;
- risultati di eventi sportivi;
- ….
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
3
Il concetto di probabilità
Cosa si intende per probabilità di un evento?
1. Definizione classica
2. Definizione frequentista
3. Definizione soggettivista
4. Definizione assiomatica
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
4
1. Definizione classica
La probabilità P(A) di un evento A è definita come il
rapporto tra il numero NA dei risultati favorevoli (ovvero il
numero dei risultati che determinano A) e il numero N
dei risultati possibili:
NA
P ( A) =
N
purché i risultati siano ugualmente possibili e
mutuamente escludentisi
E’ una definizione aprioristica, in quanto la
probabilità P(A) è definita senza far ricorso ad
alcuna effettiva prova sperimentale.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
5
Esempio Considerato l’esperimento casuale del lancio di una moneta non
truccata, il numero dei risultati possibili di un lancio è 2. La probabilità di
ottenere “testa” da un singolo
g lancio è ppari a:
Numero di casi favorevoli
1
P (testa ) =
2
Numero di facce, ovvero numero
di risultati possibili
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
6
Esempio Considerato l’esperimento casuale del lancio di un dado simmetrico e
omogeneo il numero dei risultati possibili di un lancio è 66. La probabilità
omogeneo,
di ottenere un numero pari da un singolo lancio è pari a:
3 1
P ( pari ) = =
6 2
Infatti il numero dei risultati favorevoli è 3 ed essi
corrispondono alle facce 2, 4, 6. I risultati possibili
sono, in questo caso, mutuamente escludentisi.
Esempio Si consideri l’esperimento casuale del lancio di due dadi simmetrici ed
omogenei. La probabilità di totalizzare 8 da un singolo lancio è data da:
P{8} = P{(2 + 6) ∪ (3 + 5) ∪ (4 + 4) ∪ (5 + 3) ∪ (6 + 2)}
Gli eventi sono, in qquesto caso,
mutuamente escludentisi e le
probabilità dei singoli eventi
sono uguali tra loro
1
5
P {8} = 5 ⋅ =
36 36
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
1 1 1
P {( 2 + 6 )} = ⋅ =
6 6 36
Per eventi mutuamente escludentisi, la
probabilità dell’evento unione è pari alla
somma delle probabilità dei singoli eventi
7
Esempio
p Si consideri l’esperimento
p
casuale dell’estrazione di una carta da un
mazzo di 52 carte ben mescolate.
pp una
Qual è la pprobabilità di estrarre un asso oppure
carta di fiori?
Si potrebbe pensare erroneamente che il numero dei risultati
favorevoli siano la somma degli assi (4) e delle carte di fiori (13).
In realtà, l’asso di fiori soddisfa sia al requisito di essere un asso, sia
al requisito di essere una carta di fiori. I due risultati non sono
mutuamente escludentisi.
P=
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
16
52
Il numero dei risultati favorevoli
è quindi 16 e non 17
8
2. Definizione frequentista
Si definisce frequenza assoluta nA , o semplicemente
frequenza, di un evento A il numero delle volte in cui si è
presentato l’evento favorevole.
Si definisce frequenza relativa fA il rapporto tra il
numero delle volte in cui si è presentato l’evento
favorevole e il numero N delle volte in cui è ripetuto
l’esperimento nelle medesime condizioni.
nA
fA =
N
OSS: La probabilità dell’evento A è il limite della
frequenza relativa quando il numero N
delle prove tende ad infinito
E’ una d
definizione
fi i i
a posteriori,
t i i in
i quanto
t lla d
definizione
fi i i
della probabilità P(A) implica l’ipotesi preliminare che le
prove siano ripetute in condizioni identiche
identiche.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
9
Esempio Considerato l’esperimento casuale del lancio di una moneta non
truccata, si vuole stimare la probabilità di ottenere “testa” da un singolo
lancio.
Si eseguono N=500 lanci e si calcolano la frequenza assoluta nTESTA e la frequenza
relativa fTESTA.
TESTA
Lancio
1
2
3
4
5
6
7
8
9
10
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
Risultato
CROCE
TESTA
CROCE
TESTA
CROCE
CROCE
TESTA
TESTA
CROCE
TESTA
10
Frequenza assoluta “n
nTESTA”
300
Freque nza assolutta
250
200
La frequenza assoluta aumenta
al crescere del numero di
prove (aumenta il numero di
lanci in cui si ottiene “TESTA”)
150
100
50
0
0
100
200
300
400
500
600
Numero prove
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
11
Frequenza relativa “ffTESTA”
1.0
0.9
Frequenzza relativa
0.8
0.7
0.6
05
0.5
0.4
0.3
Tende
e de a 00.55 aal ccrescere
esce e de
del
numero di prove
0.2
0.1
0.0
0
100
200
300
400
500
600
Numero prove
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
12
3 Definizione soggettivista
3.
La
ap
probabilità
obab tà d
di u
un e
evento
e to è il g
grado
ado d
di fiducia
duc a cche
e ssi ha
a
nel verificarsi di esso.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
13
4. Definizione assiomatica
La formalizzazione matematica risale a Kolmogorov (1933)
¾ Si definisce fenomeno aleatorio un fenomeno empirico
caratterizzato dalla proprietà che la sua osservazione in un
insieme fissato di circostanze non conduce sempre agli
stessi risultati.
¾ Si definisce spazio campione Ω l’insieme costituito da
tutte le possibili osservazioni (tutti i risultati possibili a
priori)
¾ Si definisce evento A un qualsiasi insieme di risultati ω,
ovvero un sottoinsieme dello spazio campione Ω relativo
al medesimo fenomeno aleatorio
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
14
¾ Se un risultato ω ∈ A , si dice che esso
realizza l’evento A. Se l’insieme A ⊂ Ω
è costituito da un solo elemento ω,
allora A si chiama evento elementare,
altrimenti A è un evento composto.
ω
Ω
A
ω∈A⊂Ω
¾ La totalità degli eventi forma lo spazio degli eventi.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
15
Logica degli eventi
1. Dati due eventi A,B ⊂ Ω , si
dice che A implica B se A ⊂ B
B
A
2. Due eventi A,B ⊂ Ω sono incompatibili
ovvero mutuamente escludentisi se non
esiste alcun risultato ω che realizzi sia A
che B, ovvero se A ∩ B = ∅ dove ∅ è
l’insieme vuoto.
3. Se due eventi A,B ⊂ Ω non sono
incompatibili ll’insieme
incompatibili,
insieme non vuoto
A ∩ B è costituito da tutti i risultati ω
che realizzano sia A sia B.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
B
B
A
A
A∩ B
16
4 Dati due eventi A,B
4.
A B ⊂ Ω , ll’insieme
insieme
è costituito da tutti i risultati A∪B
che realizzano A oppure B.
5. Dato un evento A⊂ Ω , se esso non
si realizza, allora si realizza l’evento
complementare A = Ω \ A detto
evento negazione dell’evento A.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
B
A
A
A
17
Esempio
p
Si consideri una struttura costituita da due aste incernierate.
Vediamo quale relazione sussiste tra gli insiemi “crollo della
struttura”, “rottura dell’asta 1” e “rottura dell’asta 2”.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
18
La struttura reticolare crolla se cede ll’asta
asta 1 oppure l’asta
l asta 2:
crollo della struttura = rottura dell’asta 1 ∪ rottura dell’asta 2
La rottura dell’asta 1 si verifica quando la sollecitazione S1 supera la resistenza R1.
La stessa cosa vale per la seconda asta.
Consideriamo il caso in cui R1 = R2 = R
R. Dimostrare che vale la seguente relazione
tra gli insiemi “rottura dell’asta 1” e “rottura dell’asta 2”:
rottura dell' asta 2
rottura dell' asta 1
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
19
Assiomi di Kolmogoroff
Ad ogni evento A è possibile associare la probabilità
P(A) che si verifichi l’evento.
La probabilità è una funzione che soddisfa i seguenti assiomi:
9
P(Ω) = 1
9
9
P(A) ≥ 0
se A1,A2,…,An,… sono eventi mutuamente escludentisi
(Ai ∩ Aj = ∅) per i ≠ j con i, j=1, 2, …, n,…, allora:
⎡∞ ⎤ ∞
P ⎢U Ai ⎥ = ∑ P[Ai ]
⎣ i =1 ⎦ i =1
(proprietà additiva della funzione probabilità tra due eventi tra loro
incompatibili))
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
20
Conseguenze degli assiomi
( )
1. P Ai = 1 − P ( Ai )
Per il primo assioma, vale P(Ω ) = P Ai ∪ Ai = 1
Poichè Ai e il suo complementare sono incompatibili, facendo
ricorso al terzo assioma, si ottiene P( Ai ) + P Ai = 1
(
)
( )
2. P ( Φ ) = 0
L’insieme vuoto è il complementare di Ω , quindi P ( Φ ) = 1 − P ( Ω )
( )
3. Ai ⊂ A j ⇒ P ( Ai ) ≤ P A j
Applicando il terzo assioma agli eventi incompatibili Ai e (Aj \ Ai) ,
( ) (
(
))
(
)
si ha P A j = P Ai ∪ A j \ Ai = P ( Ai ) + P A j \ Ai . Poichè l’insieme
(Aj \ Ai) non è vuoto per ipotesi, risulta P A j \ Ai ≥ 0
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
(
)
21
(
)
( ) (
4 Ai ∩ A j ≠ Φ ⇒ P Ai ∪ A j = P ( Ai ) + P A j − P Ai ∩ A j
4.
)
Questa proprietà è la generalizzazione del secondo assioma per
eventi non incompatibili.
Si consideri
id i l’evento
l’
unione:
i
(
Ai ∪ A j = Ai ∪ Ai ∩ A j
)
Unione di due eventi
incompatibili
Ω
Aj
Ai
Ai ∩ A j
Ai ∩ A j
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
22
(
)
Per il terzo assioma,, risulta P (Ai ∪ A j ) = P( Ai ) + P Ai ∩ A j (*)
()
Sapendo che anche l’evento Aj è esprimibile come unione di due
⎛
⎞
eventi incompatibili Aj = ⎛⎜⎝ Ai ∩ Aj ⎞⎟⎠ ∪ ⎜ Ai ∩ Aj ⎟ , il terzo assioma
⎝
(
⎠
permette di scrivere P (A j ) = P(Ai ∩ A j ) + P Ai ∩ A j
Dalle relazioni (*) e (**) si ottiene:
(
)
( ) (
) (**)
P Ai ∪ A j = P ( Ai ) + P A j − P Ai ∩ A j
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
)
23
Probabilità condizionata
Si definisce probabilità condizionata dell’evento Ai dato
l’evento Aj , con Ai e Aj eventi qualunque, il rapporto:
(
)
P Ai | A j =
(
P Ai ∩ A j
( )
P Aj
)
( )
P Aj ≠ 0
Indica la probabilità che si verifichi l’evento Ai
sapendo che Aj si è verificato.
verificato
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
24
OSSERVAZIONI:
Se Ai ⊂ A j, allora Ai ∩ A j = Ai e quindi:
(
)
P Ai | A j =
P ( Ai )
( )
P Aj
> P ( Ai )
Se Ai ⊃ A j, allora Ai ∩ A j = A j e quindi:
(
)
P ( Ai | A j ) =
=1
P ( Aj )
P Aj
Se Ai e Aj sono incompatibili, allora Ai ∩ Aj = ∅
eq
quindi:
P (Ai | A j ) = 0
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
25
Esempio
p
Si consideri l’esperimento
p
casuale del lancio di due dadi simmetrici
ed omogenei, nel quale la somma dei risultati è un numero pari
(Aj). La probabilità di totalizzare 8 da un singolo lancio è :
Probabilità che si verifichi l’evento
Ai [Ai = {8} ={(2+6)∪(3+5) ∪…}]
sapendo che Aj si è verificato
[Aj = {pari}].
{ i}]
(
)
P Ai | A j =
(
P Ai ∩ A j
( )
)
P Aj
Esempio già svolto
5
P{8 ∩ parii}
P{8}
5
36
P{8 pari} =
=
=
=
P{pari} 0.5 18
P{pari}
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
26
Eventi indipendenti
p
Due
ue e
eventi
e Ai e Aj ssi d
dicono
co o stat
statisticamente
st ca e te indipendenti
d pe de t
se il verificarsi di uno non influisce sulla probabilità che
si verifichi l’altro.
Esempio Si consideri l’esperimento casuale del lancio di un dado non truccato.
Stabilire se gli eventi A={ottengo un numero dispari dal lancio del dado}
e B={ottengo il numero 1 dal lancio del dado} sono indipendenti.
Lo spazio campione Ω è {1, 2, 3, 4, 5, 6}. Dalla definizione, se gli
eventi A e B sono indipendenti, il verificarsi di un evento non influenza
la probabilità che l’altro si verifichi.
Ad esempio,
esempio si calcola P(B|A) e P(B): queste due probabilità sono
uguali se gli eventi sono indipendenti.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
27
• P(B|A)
( | ) = probabilità
p
di ottenere il risultato “1”, sapendo
p
che si è verificato un
risultato dispari.
1
P (B ∩ A) 6 1
= =
P (B | A ) =
1 3
P ( A)
2
Infatti: A={1, 3, 5}, B={1} e B∩A={1}
• P(B) = probabilità di ottenere il risultato “1” è pari a 1/6
Si osserva che P(B|A) e P(B): non sono uguali,
uguali quindi gli eventi A e B non sono
indipendenti.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
28
Eventi indipendenti
p
Nel
e caso d
di due e
eventi
e Ai e Aj stat
statisticamente
st ca e te indipendenti
d pe de t
valgono le seguenti relazioni:
(
)
( )
• P Ai ∩ A j = P ( Ai ) P A j
(
)
= P ( Ai )
• P ( Ai | A j ) = P ( Ai )
P ( Aj )
P Aj
(
)
P ( Ai )
( ) P ( A ) = P ( Aj )
i
• P A j | Ai = P A j
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
( )
se
P Aj ≠ 0
se
P ( Ai ) ≠ 0
29
OSS: Il concetto di indipendenza è diverso dal concetto di
incompatibilità: due eventi incompatibili [la cui intersezione
è l’insieme vuoto] sono dipendenti statisticamente!
Infatti il verificarsi di un evento esclude il verificarsi
dell’altro.
Se due eventi Ai e Aj sono statisticamente indipendenti
indipendenti,
allora:
(
)
( )
( )
P Ai ∪ A j = P ( Ai ) + P A j − P ( Ai ) P A j
Dati n eventi,
eventi essi si dicono statisticamente indipendenti
se e solo se, per qualunque sottoinsieme {A1,…, An} di n
eventi, si verifica la seguente condizione:
⎛ n ⎞ n
P⎜⎜ I Ai ⎟⎟ = ∏ P ( Ai )
⎝ i =1 ⎠ i =1
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
30
Teorema delle probabilità totali
Sia A1,…, An una collezione di eventi mutuamente
n
escludentisi ed esaustivi (Ω = U Ai ) e P(Ai) ≠ 0 per
i=1
ogni i=1, 2, …, n.
Qualunque sia l’evento C, si ha:
n
P ( C ) = ∑ P ( C | Ai ) ⋅ P ( Ai )
i =1
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
31
Formula di Bayes
Sia A1,…, An una collezione di eventi mutuamente
n
escludentisi ed esaustivi (Ω = U Ai ) e P(Ai) ≠ 0 per
i=1
ogni i=1, 2, …, n.
Qualunque sia C ⊂ Ω ,si ha:
P( Ai | C ) =
P(C | Ai )P( Ai )
∑ P(C | A )P(A )
n
j =1
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
j
j
32
Esempio Un edificio crolla. Le possibili cause di crollo sono:
A)) deterioramento;
B) eccessivo sovraccarico;
C) esplosione;
D) errore di progettazione;
E) errore in fase di costruzione.
Si suppone che le cause siano mutuamente escludentisi ed esaustive
B
A
spazio
i campione
i
D
E
C
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
33
Sulla base di analisi effettuate su altri edifici della stessa tipologia,
Si conosce la pprobabilità di ciascuna causa:
• P(A)=0.40;
• P(B)=0.35;
• P(C)=0.05;
P(C) 0.05;
• P(D)=0.10;
• P(E)=0.10.
Sulla base di indagini su crolli di edifici della stessa tipologia, si
conosce la probabilità di crollo condizionale a ciascuna causa:
• P(crollo | A)=0.60;
A) 0 60;
• P(crollo | B)=0.35;
• P(crollo | C)=0.70;
• P(crollo | D)=0.40;
• P(crollo | E)=0.40.
Si chiede di determinare la causa di crollo più probabile.
.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
34
Applicando la formula di Bayes, si ottiene la probabilità che
ciascuna causa sia il motivo del crollo.
Ad esempio, per la causa A: P{A | crollo} =
P{crollo | A}⋅ P{A}
P{crollo}
P(crollo) = P(crollo | A)P(A) + P(crollo | B)P(B) + P(crollo | C)P(C) +
P(crollo | D)P(D) + P(crollo | E)P(E) =
= 0.6
0 6·00.44 + 00.35
35·00.35
35 + 00.77·00.05
05 + 00.44·00.11 + 0.4
0 4·00.11 =
= 0.4775
P(A | crollo) = 00.6·0.4
6 0 4 / 00.4775
4775 = 00.50
50
P(B | crollo) = 0.35·0.35 / 0.4775 = 0.26
P(C | crollo) = 0.7·0.05 / 0.4775 = 0.07
P(D | crollo) = 0.4·0.1 / 0.4775 = 0.08
P(E | crollo) = 0.4·0.1 / 0.4775 = 0.08
Si conclude che il deterioramento (causa A) sia la causa più
probabile di crollo dell’edificio.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
35
Esempio L’urna A contiene 2 palline bianche e 3 nere; l’urna B ne contiene 4
bianche e 1 nera, l’urna C ne contiene 3 bianche e 4 nere. Si
sceglie a caso un’urna e si estrae una pallina bianca. La probabilità
che provenga dall’urna C è calcolata nel seguente modo.
spazio campione
E
A
C
B
L’evento
L’
t A iindica
di l’estrazione
l’ t i
di una pallina
lli ddall’urna
ll’
A
A. A
Analogamente,
l
t
si definiscono gli eventi B e C. Ovviamente gli eventi A, B, C sono
mutuamente escludentisi ed esaustivi. Quindi le probabilità di scegliere
una delle tre urne sono uguali tra loro e pari a 1/3.
L’evento E indica l’estrazione di una pallina bianca, evento che può
presentarsi in concomitanza con qualunque degli eventi A,
A B
B, C
C.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
36
Applicando la formula di Bayes, si ottiene la probabilità di aver
estratto una ppallina bianca dall’urna C.
P{C | E} =
P{C}⋅ P{E | C}
P{E}
La probabilità di estrarre una pallina bianca da una qualsiasi urna è
pari a:
P{E} = P{(E ∩ A) ∪ (E ∩ B ) ∪ (E ∩ C )} =
= P{(E ∩ A)}+ P{(E ∩ B )}+ P{(E ∩ C )} =
= P{A}P{E A}+ P{B}P{E B}+ P{C}P{E C} =
1 2 1 4 1 3 57
= ⋅ + ⋅ + ⋅ =
3 5 3 5 3 7 105
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
37
La probabilità P{E|A} di estrarre una pallina bianca dall’urna A è pari a:
P{E A} =
(bianche )urnaAA = 2
(bianche + nere )urnaA 5
In modo analogo si calcolano P{E|B} e P{E|C}
(bianche )urnaB = 4
(bianche + nere )urnaB 5
(bianche )urnaC = 3
P{E C } =
(bianche + nere )urnaC 7
P{E B} =
In conclusione:
1 3
P {C} ⋅ P { E C} 3 ⋅ 7 5
P {C E} =
=
=
57
P { E}
19
105
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
38
Variabili aleatorie
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
39
Variabili aleatorie
La variabile aleatoria X : Ω→R è definita come una
f
funzione
i
avente
t come dominio
d i i lo
l spazio
i campione
i
Ω
e come codominio l’insieme dei numeri reali
Esempio Si consideri l’esperimento del lancio di due dadi non truccati.
Lo spazio campione Ω contiene i 36 possibili risultati:
Ω= {(1,1),
Ω
{(1 1) (1,2),
(1 2) … , (6,5),
(6 5) (6
(6,6)}
6)}
Si definisce, a titolo di esempio, la variabile aleatoria X che
rappresenta la somma dei risultati di due lanci di un dado non
truccato.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
40
Risultato Risultato Valore della 1° lancio 2° lancio variabile X
1
1
2
1
2
3
1
3
4
1
4
5
1
5
6
1
6
7
2
1
3
2
2
4
2
3
5
2
4
6
2
5
7
2
6
8
3
1
4
3
2
5
3
3
6
3
4
7
3
5
8
3
6
9
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
Risultato Risultato Valore della 1° lancio 2° lancio variabile X
4
1
5
4
2
6
4
3
7
4
4
8
4
5
9
4
6
10
5
1
6
5
2
7
5
3
8
5
4
9
5
5
10
5
6
11
6
1
7
6
2
8
6
3
9
6
4
10
6
5
11
6
6
12
41
Le variabili aleatorie sono classificate in:
discrete (es. risultato del lancio di un dado, il numero di
veicoli che attraversano un incrocio in un’ora
un ora,…))
continue (es. azioni applicate alle strutture, resistenze
dei materiali, …)
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
42
Funzione di distribuzione cumulativa
(
(v.a.
continue)
ti
)
La funzione di distribuzione cumulativa FX (x ) di una v.a. X
esprime la probabilità che X assuma valori inferiori o uguali al
numero reale x:
FX ( x ) = P ( X ≤ x )
La funzione di distribuzione cumulativa misura la probabilità
che X(ω) assuma valori minori o uguali al numero reale x e
gode delle seguenti proprietà:
è sempre non negativa
è monotona non decrescente tra 0 e 1
lim x → -∞ Fx(x) ≡ Fx (- ∞) = 0
lim x → +∞ Fx(x) ≡ Fx (+ ∞) = 1
9 è continua a destra lim ξ → x+ Fx(ξ) ≡ Fx (x
( +) = Fx(x)
( )
9
9
9
9
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
43
La probabilità che una variabile aleatoria X assuma
valori in un intervallo (x1, x2] è data da:
P (x1 < X ≤ x2 ) = FX (x2 ) − FX (x1 )
Infatti:
( −∞, x2 ] = ( −∞, x1 ] ∪ ( x1 , x2 ]
Gli eventi a secondo membro sono
incompatibili, quindi
P( X ≤ x2 ) = FX ( x2 ) = P( X ≤ x1 ) + P( x1 < X ≤ x2 ) =
= FX ( x1 ) + P( x1 < X ≤ x2 )
OSS: Nel caso di variabili aleatorie continue, la probabilità che X assuma
il valore x1 è nulla
nulla, perchè x1 è un insieme di misura nulla
nulla. Quindi
per le variabili aleatorie continue vale:
P( x1 ≤ X ≤ x2 ) = P( X = x1 ) + P( x1 < X ≤ x2 ) = FX ( x2 ) − FX ( x1 )
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
44
Funzione di densità di probabilità
(v.a. continue)
Data una variabile aleatoria X continua, si definisce
la funzione fx(x):R
( ):R→[0,+
[0 +∞) tale per cui
FX ( x ) =
x
∫
f X ( x ) ⋅dx
−∞
è detta funzione di densità di probabilità e gode delle
seguenti proprietà
1.
f X ( x ) ≥ 0, ∀x ∈ R
+∞
2.
∫ f (x )dx = 1
X
−∞
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
45
L’integrale della funzione di densità di probabilità misura
la probabilità che X assuma valori inferiori o eguali al
numero reale x
La quantità elementare dP = dFx(x) = fx(x)·dx misura la
probabilità elementare che X assuma valori nell’intervallo
((x,, x+dx]]
P( x < X ≤ x + dx ) = FX ( x + dx ) − FX ( x ) =
x + dx
∫ f (t )dt = f (x )dx
X
X
x
Dalla definizione di densità di probabilità, si ricava:
dFX ( x )
f X (x ) =
dx
Quindi la funzione densità di probabilità è uguale alla derivata prima della funzione di
distribuzione cumulativa della variabile aleatoria.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
46
PDF
fX(x)
FX ( b ) =
b
∫
f X ( x ) ⋅ dx
−∞
a
b
CDF
FX(x)
P ( a < X ≤ b ) = FX ( b ) − FX ( a )
FX(b)
FX(a)
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
FX(b)
47
p%
Il p
percentile p
p% della variabile X è
definito come il valore argomentale
(ossia il valore della variabile) yp l a
cui probabilità cumulata vale proprio
p/100
FX(a)
Il percentile rappresenta in definitiva la
lettura in modo inverso della funzione di
probabilità cumulata FX
FX(x)
CDF
a
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
yp
48
Momenti di variabili aleatorie
I momenti sono importanti indicatori di determinate
proprietà della generica variabile aleatoria X(ω)
Si definisce momento di ordine q di una variabile
aleatoria X(ω) dotata di funzione di densità di
probabilità, la quantità:
+∞
{ } ∫ x f (x )dx
E Xq =
q
X
−∞
+∞
q
|
x
∫ | f X (x )dx
per q intero positivo,
positivo
se esiste finito l’integrale
−∞
OSS: Poichè fx(x) ≥ 0 , i momenti di ordine pari sono sempre non negativi.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
49
Momento del primo ordine - valore atteso
(valore medio)
Si definisce valore atteso μX di una variabile aleatoria X(ω) il
momento del primo ordine
E {X } =
+∞
∫
x ⋅ f X ( x ) dx
−∞
Esso è un parametro di posizione della distribuzione e si può
i t
interpretare
t
come il baricentro
b i
t d
della
ll di
distribuzione
t ib i
di
probabilità definita dalla funzione di densità di probabilità fx(x)
Proprietà del valore atteso: Proprietà di linearità
Date n variabili aleatorie X1, X2,…, Xn, la media di una loro combinazione lineare è uguale
alla combinazione lineare delle medie:
E{a1 X 1 + a2 X 2 + ... + an X n } = a1 E{X 1}+ a2 E{X 2 }+ ... + an E{X n }
p
deriva dalla pproprietà
p
di linearità dell’integrale
g
che definisce il valore atteso.
Questa pproprietà
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
50
Momento del secondo ordine
I momenti di ordine superiore al primo vengono
spesso calcolati rispetto al valore medio μX della
variabile aleatoria X
Si definisce varianza il momento centrale del secondo
ordine ed è calcolato nel seguente modo:
Var [ X ] = σ X2 = E
{
( X − μX )
2
}
+∞
=
∫ ( x − μ X ) f X ( x ) dx
2
−∞
Esso è un parametro di posizione della distribuzione e si può
interpretare come il momento di inerzia della distribuzione di
probabilità definita dalla funzione di densità di probabilità fx(x)
rispetto alla retta baricentrica x = μX.
OSS:
La varianza misura la dispersione della distribuzione rispetto al suo valore
medio.
Si definisce deviazione standard la radice quadrata positiva della varianza.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
51
Al crescere della varianza,, diminuisce la probabilità
p
che tutte
le realizzazioni x della variabile aleatoria X siano
concentrate attorno al valore medio μX.
μ = 10, σ = 3
μ = 10, σ = 5
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
52
Vettori aleatori
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
53
Vettori aleatori
Il vettore
e o e aleatorio
a ea o o X a n d
dimensioni
e s o è de
definito
o co
come
e
l’insieme { X 1 , X 2 ,..., X n } di n variabili aleatorie che opera la
trasformazione Ω → R n associando ad ω l’ennupla:
p
{ x1 , x2 ,..., xn } ∈ R n
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
54
Funzione di distribuzione cumulativa
Si definisce funzione di distribuzione cumulativa
congiunta del vettore aleatorio X, la funzione:
FX (x ) = P{( X 1 ≤ x1 ) ∩ ( X 2 ≤ x2 ) ∩ ... ∩ ( X n ≤ xn )}
T l funzione
Tale
f
i
misura
i
lla probabilità
b bilità che
h sii verifichino
ifi hi tutti
t tti
gli eventi ( X 1 ≤ x1 ) , ( X 2 ≤ x2 ) , .. , ( X n ≤ xn.)
La funzione di distribuzione cumulativa gode delle seguenti proprietà:
•
•
è sempre non negativa
è monotona non decrescente tra 0 e 1
•
lim xi → −∞
FX (x ) = 0
∀x j \ xi
•
lim xi → +∞
FX (x ) = 1
∀x j \ xi
•
è continua a destra in ciascuna variabile.
variabile
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
55
Funzione di densità di probabilità
Si definisce
S
de sce funzione
u o ed
di de
densità
s tà d
di p
probabilità
obab tà co
congiunta
g u ta
del vettore aleatorio X, la funzione:
∂ n FX (x )
f X (x ) =
∂x1∂x2 ...∂xn
e gode delle seguenti proprietà:
1.
f X (x ) ≥ 0, ∀x ∈ R n
+∞
2.
∫ ... ∫ f (x ) dx dx ...dx
X
−∞
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
+∞
1
2
n
=1
−∞
56
Funzione di distribuzione marginale
Si definisce funzione di distribuzione marginale
del vettore aleatorio X, la funzione:
FX i ( xi ) =
+
+∞
+∞
+
∫ ... ∫
−∞
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
−∞
f uuXr
r
x ⋅ dx1 ⋅ dx2 ...dxi −1 ⋅ dxi +1...dxn = 1
()
57
Esempio:
se p o vettore
etto e co
composto
posto da due variabili
a ab X e Y
- La funzione di distribuzione cumulativa congiunta si esprime come:
- Funzione di densità di probabilità congiunta
densità di probabilità congiunta
se X e Y sono indipendenti
probabilità di estrazione della coppia di
valori x , y in un intervallo dx dy
- La probabilità marginale di una variabile (escludendo cioè l’effetto dell’altra) vale
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
58
Momenti congiunti di vettori aleatori
Si considerano due variabili aleatorie X e Y.
Si definisce momento congiunto di ordine (p+q),
l’integrale doppio:
{
+∞+∞
} ∫ ∫x
E X qY p =
q
y p f XY (x, y )dxdy
p e q sono interi
positivi
− ∞− ∞
Si definisce momento centrale congiunto di
ordine (p+q) il seguente integrale doppio:
E
{
( X − μ X ) (Y − μY )
p
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
q
}
+∞ +∞
=
∫
∫ ( x − μX )
p
( y − μY ) f XY ( x, y ) ⋅ dx ⋅ dy
q
−∞ −∞
59
Il momento centrale congiunto di secondo ordine è
d tt covarianza:
detto
i
Cov ( X , Y ) = E {( X − μ X ) (Y − μY )} =
+∞ +∞
=
∫ ∫ ( x − μ ) ⋅ ( y − μ ) ⋅ f ( x, y ) ⋅ dx ⋅ dy
X
Y
XY
−∞
∞ −∞
∞
Cov ( X , Y ) = E { X Y } − μY ⋅ E { X } − μ X ⋅ E {Y } + μ X ⋅ μY = E { X Y } − μ X ⋅ μY
E’ possibile costruire la matrice di covarianza:
E
⎡ Cov( X 1 , X 1 ) Cov( X 1 , X 2 )
⎢Cov( X , X ) Cov( X , X )
2
1
2
2
Σ=⎢
⎢
...
...
⎢
⎣Cov( X n , X 1 ) Cov( X n , X 2 )
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
... Cov( X 1 , X 2 )⎤
... Cov( X 2 , X n )⎥⎥
⎥
...
...
⎥
... Cov( X n , X n )⎦
60
Si definisce coefficiente di correlazione, la quantità:
ρ (X ,Y ) =
Cov( X , Y )
σ XσY
E’ una misura dell’interdipendenza lineare di due variabili aleatorie.
Se le variabili X e Y non sono correlate (lineramente) ρ ( X , Y ) = 0
Due variabili aleatorie si dicono statisticamente indipendenti se lo
sono gli eventi ( X ≤ x ) e (Y ≤ y ) . Vale la seguente relazione:
P {( X ≤ x ) ∩ (Y ≤ y )} = P ( X ≤ x ) ⋅ P (Y ≤ y )
FXY ( x, y ) = FX ( x ) ⋅ FY ( y )
{
+∞
} ∫x
E X qY p =
−∞
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
f XY ( x, y ) = f X ( x ) ⋅ fY ( y )
+∞
q
⋅ f X ( x ) ⋅dx ∫ y p ⋅ fY ( y ) ⋅dy
−∞
61
Due variabili aleatorie indipendenti
p
sono anche non correlate:
E{XY } = μ X μY
Cov( XY ) = 0
ma non è valida
lid l’implicazione
l’i li
i
iinversa.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
62
Algebra delle variabili casuali
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
63
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
64
Le distribuzioni e loro
pp
nella
applicazione
modellazione delle
caratteristiche dei
materiali e delle azioni
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
65
Resistenze dei materiali
Le
ed
distribuzioni
st bu o ut
utilizzate
ate so
sono,
o, in ge
generale,
e a e, la
a
distribuzione normale e la log-normale.
Resistenze:
Coefficiente di variazione Distribuzione
Compressione
p
CLS
15 %
LN
Trazione acciaio
8%
LN
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
66
1. Distribuzione normale N(μ ,σ)
Valore medio
μ
Deviazione standard
σ
Funzione di densità di
probabilità (PDF)
⎡ 1 ⎛ x − μ ⎞2 ⎤
1
exp ⎢− ⎜
f X (x ) =
⎟ ⎥
σ 2π
⎢⎣ 2 ⎝ σ ⎠ ⎥⎦
Funzione di distribuzione
cumulativa
l ti (CDF)
2
⎡
1
1⎛t −μ ⎞ ⎤
FX ( x ) = ∫
exp ⎢− ⎜
⎟ ⎥ dt
− ∞σ 2π
⎣⎢ 2 ⎝ σ ⎠ ⎥⎦
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
x
67
Distribuzione normale N(μ ,σ)
PDF
σ
σ
- simmetrica rispetto al valor medio μ
- 2 flessi a μ ± σ
μ
CDF
- antisimmetrica rispetto al punto (μ,0.5)
- FX(μ) = 0.5
05
μ
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
68
La PDF e la CDF cambiano forma
e pposizione al variare di μ e σ
PDF
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
μ controlla la posizione sull’asse
delle ascisse
CDF
69
La PDF e la CDF cambiano forma
e posizione al variare di μ e σ
σ controlla l’apertura della PDF e
la pendenza della CDF
μ
μ
PDF
CDF
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
70
OSS: È utile definire una variabile standardizzata Z
z=
x−μ
⎡ z2 ⎤
1
f ( z) = ϕ ( z) =
⋅ exp ⎢ − ⎥
2π
⎢⎣ 2 ⎥⎦
σ
riconduce il problema allo studio di
una gaussiana con μ =0 e σ =1
La CDF Φ(z) è data ovviamente dall’integrale della φ(z):
z
F ( z ) = Φ( z ) = ∫
−∞
⎡ z2 ⎤
1
exp ⎢ − ⎥ dz
2π
⎢⎣ 2 ⎥⎦
I valori della Φ(z) sono tabellati
Sono inoltre tabellati anche i valori zp della
variabile standardizzata corrispondenti a valori
percentili p “notevoli”.
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
71
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
72
Si dimostra che sostituendo σ = (x-μ) / z nella definizione di fX(x)
x
z
∫x f X ( x) ⋅ dx = ∫z ϕ ( z ) ⋅ dz
2
2
1
1
FX ( x) = Φ ( z )
Essendo la distribuzione φ(z) simmetrica, Φ
risulta antisimmetrica rispetto al punto (0,0.5) per cui
Le probabilità calcolate con la variabile
normalizzata Z sono uguali alle
probabilità calcolate con la variabile
effettiva X
Φ (-z) = 1 - Φ (z)
CDF normalizzata
p
Tenendo conto del cambio di variabile,
si può facilmente calcolare i percentili xp
a partire dai percentili della variabile z
xp = μ + σ · zp
FX (a)
a
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
zp
73
2. Distribuzione log-normale N(μL ,σL)
Valore medio
Deviazione standard
Parametro
ζ
Parametro
λ
μL
σL
⎛ σ L2 ⎞
ζ = ln ⎜⎜1 + 2 ⎟⎟
⎝ μL ⎠
1 2
λ = ln (μ L ) − ζ
2
2
⎡
1
1 ⎛ ln ( x ) − λ ⎞ ⎤
Funzione di densità di
⎟⎟ ⎥
f X (x ) =
exp ⎢− ⎜⎜
probabilità (PDF)
ζx 2π
⎠ ⎥⎦
⎣⎢ 2 ⎝ ζ
2
x
Funzione di
⎡
1
1 ⎛ ln
l (t ) − λ ⎞ ⎤
distribuzione cumulativa FX ( x ) = ∫
⎟⎟ ⎥ dt
exp ⎢− ⎜⎜
(CDF)
⎢⎣ 2 ⎝ ζ
⎠ ⎥⎦
0 + ζ t 2π
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
74
LN (μ L = 10, σ L = 5)
N (μ N = 10, σ N = 5)
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
75
Variazione della PDF e della CDF al variare ζ per λ = 1
PDF
CDF
ζ
ζ
ζ
ζ
ζ
ζ
Moda
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
Mediana
76
Variazione della PDF e della CDF al variare λ per ζ = 1
PDF
CDF
λ
λ
λ
λ
λ
λ
Mediana
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
77
Azioni
Le
ed
distribuzioni
st bu o ut
utilizzate
ate d
dipendono
pe do o da
dal ttipo
po d
di a
azione:
o e
Azione
Coefficiente di variazione Distribuzione
Carichi permanenti:
portato
Permanente p
10 %
N
Peso proprio CLS
6%
N
proprio
p acciaio
Peso p
4%
N
Carichi variabili:
20 %
G
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
78
1. Gumbel G((μG ,σG)
Parametro
α
fattore di forma
Parametro
β
fattore di scala
Valore medio
Deviazione standard
μG = β +
σG =
0.5772
π
α
α 6
Funzione di densità di
probabilità (PDF)
f X (x ) = α exp [− α (x − β ) − exp (− α ( x − β ))]
Funzione di
distribuzione cumulativa
(CDF)
FX (x ) = exp [− exp (− α (x − β ))]
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
79
(α = 2, β = 1)
(α = 2, β = 10)
(α = 1, β = 1)
(α = 1, β = 10)
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
80
Distribuzioni di base
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
81
Parametri statistici di funzioni di
variabili aleatorie
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
82
Frattile di variabili aleatorie
Politecnico di Torino - Ingegneria
Tecnica delle Costruzioni – Probabilità
83