Soluzioni prova scritta di Complementi di Probabilità e Statistica (29/06)
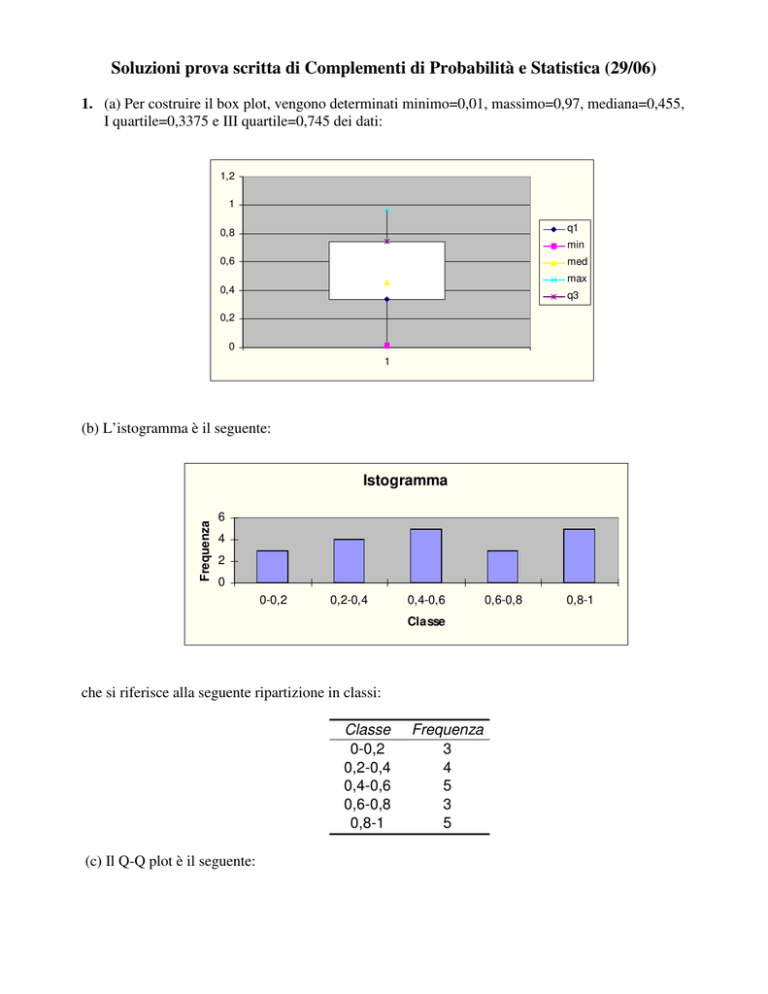
1. (a) Per costruire il box plot, vengono determinati minimo=0,01, massimo=0,97, mediana=0,455,
I quartile=0,3375 e III quartile=0,745 dei dati:
1,2
1
0,8
q1
0,6
med
min
max
0,4
q3
0,2
0
1
(b) L’istogramma è il seguente:
Frequenza
Istogramma
6
4
2
0
0-0,2
0,2-0,4
0,4-0,6
Classe
che si riferisce alla seguente ripartizione in classi:
Classe
0-0,2
0,2-0,4
0,4-0,6
0,6-0,8
0,8-1
(c) Il Q-Q plot è il seguente:
Frequenza
3
4
5
3
5
0,6-0,8
0,8-1
1,2
1
0,8
0,6
0,4
0,2
0
0
0,2
0,4
0,6
0,8
1
Specialmente nell’ultima parte, il grafico non evidenzia un andamento lineare. Pertanto non si
ritiene valida l’ipotesi di distribuzione gaussiana.
(d) Dall’istogramma si ritiene valida l’ipotesi di legge uniforme su [0,1].
Dati ordinati
F. empirica
F teorica
Diff.
0,01
0,05
0,01
0,04
0,16
0,1
0,16
0,06
0,19
0,15
0,19
0,04
0,28
0,2
0,28
0,08
0,33
0,25
0,33
0,08
0,34
0,3
0,34
0,04
0,35
0,35
0,35
0
0,41
0,4
0,41
0,01
0,43
0,45
0,43
0,02
0,45
0,5
0,45
0,05
0,46
0,55
0,46
0,09
0,57
0,6
0,57
0,03
0,66
0,65
0,66
0,01
0,68
0,7
0,68
0,02
0,69
0,75
0,69
0,06
0,91
0,8
0,91
0,11
0,94
0,85
0,94
0,09
0,95
0,9
0,95
0,05
0,96
0,95
0,96
0,01
0,97
1
0,97
0,03
Dalle tavole per il test, per n=20 il quantile risulta 0,2940. Poiché la statistica test vale 0.11,
l’ipotesi formulata non si rigetta.
(e) Trattandosi di popolazione non gaussiana, è possibile solo effettuare un test sulla mediana.
Essendo una possibile distribuzione uniforme, la mediana coincide con la media 0,5. Vi sono 9
valori superiori alla mediana 0,5. Il valore della statistica 2*DISTRIB.BINOM(9;20;0.5;vero)=0,82
è maggiore di 0,50 pertanto l’ipotesi nulla non si rigetta.
2. (a) Per stabilire se i turni di lavoro influenzano i tempi, è necessario effettuare un’anova a 1
fattore (effetti fissi) a blocchi:
Analisi varianza: a due fattori senza replica
RIEPILOGO
Conteggio Somma
Media
Varianza
A
5
3,36
0,672
0,06367
B
5
2,43
0,486
0,13383
C
5
3,6
0,72
0,0731
D
5
2,29
0,458
0,06557
M1
4
2,27
0,5675
0,086225
M2
4
2,7
0,675
0,0247
M3
4
2,23
0,5575
0,131292
M4
4
1,66
0,415
0,094967
M5
4
2,82
0,705
0,1273
ANALISI VARIANZA
Origine della variazione
SQ
gdl
Righe
0,2586
MQ
3
F
Valore di significatività
F crit
0,0862
0,911486
0,464393
3,4903
0,55469
0,699653
3,25916
Colonne
0,20983
4 0,052457
Errore
1,13485
12 0,094571
Totale
1,60328
19
Poiché 0,9114<3.4903, le medie dei tempi di esecuzione non sono diverse per turno di lavoro.
Quindi il turno non influenza il tempo di esecuzione.
(b) Effettuando un grafico dei box plot si evince però una risposta diversa dalla precedente:
1,2
1
q1
min
med
max
q3
0,8
0,6
0,4
0,2
0
A
B
C
D
L’analisi dei residui in realtà mostra che la popolazione non è gaussiana. Inoltre l'esiguità del
campione casuale potrebbe inficiare i risultati.
1,2
1
0,8
0,6
0,4
0,2
0
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
(c) Per rispondere all’ultimo quesito è necessario fare un’analisi della varianza a 2 fattori con
repliche. I dati vanno così riorganizzati:
A
B
C
D
Giorno 1
Giorno 2
Giorno 3
0,5
0,68
0,81
0,7
0,45
0,31
0,93
0,7
0,56
0,34
0,58
0,31
0,89
0,65
0,17
0,37
0,26
0,77
0,88
0,82
0,7
0,16
0,69
0,05
0,15
0,27
0,54
0,87
0,74
0,53
1
0,76
0,62
0,61
0,6
0,41
0,79
0,38
0,43
0,31
0,58
0,05
0,89
0,2
0,64
0,4
0,57
0,19
0,51
0,17
0,32
0,35
0,65
0,07
0,86
0,82
0,59
0,17
0,6
0,44
ANALISI VARIANZA
Origine della variazione
SQ
gdl
MQ
F
Valore di significatività
F crit
Campione
0,134067
3
0,044689
0,700975
0,556104
2,79806
Colonne
0,289743
2
0,144872
2,272408
0,114044
3,190721
Interazione
0,250443
6
0,041741
0,654728
0,686138
2,294598
3,06012
48
0,063752
3,734373
59
In
Totale
L’analisi della varianza suggerisce che non sussistono interazioni tra giorni e turni. Utilizziamo
anche dei grafici.
0,8
0,7
0,6
A
B
C
D
0,5
0,4
0,3
0,2
0,1
0
Giorno 1
Giorno 2
Giorno 3
In realtà dal grafico sembrerebbe il contrario. Effettuiamo un’analisi dei residui sui livelli del fattore
turni:
70
60
50
40
30
20
10
0
-0,7
-0,5
-0,3
-0,1
0,1
0,3
0,5
Si evidenzia in alcuni punti del grafico un andamento non lineare e quindi la popolazione potrebbe
non essere gaussiana.
3.
Quadrato Greco-Latino
I
II
III
IV
V
a
A
B
C
D
E
b
E
A
B
C
D
c
D
E
A
B
C
d
C
D
E
A
B
e
B
C
D
E
A
Possibile applicazione: test su 5 macchine con l'uso di 5 piloti in 5 giorni diversi.
Soluzioni prova scritta di Complementi di Probabilità e Statistica (30/06)
1. (a) Il Q-Q plot per il set di dati Analisi I
1,20
1,00
0,80
0,60
0,40
0,20
0,00
24
25
26
27
28
29
30
Il Q-Q plot per il set di dati Fisica
1,20
1,00
0,80
0,60
Serie1
0,40
0,20
0,00
18
20
22
24
26
28
30
Dei due insiemi risulta provenire da una popolazione gaussiana maggiormente il set di dati Fisica.
(b) L'istogramma del set di dati Fisica è
Frequenza
Istogramma
5
0
18-20
21-23
24-26
Classe
con la seguente ripartizione in classi:
27-30
Classe
18-20
21-23
24-26
27-30
Frequenza
4
3
4
4
La distribuzione risulta uniforme sull'intervallo [18,30]. Eseguiamo il test di KS:
Fisica
18
19
20
21
22
23
24
25
27
28
F.empirica
0,066667
0,2
0,266667
0,333333
0,4
0,466667
0,6
0,733333
0,866667
1
F. teorica
0
0,083333
0,166667
0,25
0,333333
0,416667
0,5
0,583333
0,75
0,833333
Diff
0,066667
0,116667
0,1
0,083333
0,066667
0,05
0,1
0,15
0,116667
0,166667
Il quantile per n=15 corrispondente al livello di significatività 0,05 risulta 0.3376. Pertanto l'ipotesi
di distribuzione uniforme non si può rigettare.
(c) E' possibile effettuare una analisi anova ad un fattore (le 4 materie) a blocchi (ogni blocco è uno
studente).
ANALISI VARIANZA
a 2 fattori senza
repliche
Origine
SQ
della
variazione
Righe
84,05
Colonne
65,23333
Errore
167,7
Totale
gdl
316,9833
MQ
F
Valore di
F crit
significativ
ità
3 28,01667 7,016696 0,000626 2,827051
14 4,659524 1,166965 0,334403 1,935007
42 3,992857
59
Le medie risultano diverse (righe). Tale ipotesi è confermata dal grafico del box-plot:
30
q1
25
min
med
max
20
q3
15
Analisi
Geometria
Algebra
Fisica
e anche dal grafico degli intervalli di confidenza
30
Serie1
25
Serie2
Serie3
20
Analisi
Geometria
Algebra
Fisica
Effettuando il Fisher Test si ha poi:
Analisi
Geometria
Algebra
Fisica
Analisi
0
Geometria Algebra
1,4
1
0
0,4
0
Fisica
3,266667
1,866667
2,266667
0
che confrontato con il quantile 1,71 segnala diversi in media il set di dati di fisica rispetto a quello
di geometria e di algebra e di analisi.
(d) E' necessario effettuare un'analisi ANOVA a 1 fattore, ossia:
Analisi varianza: ad un fattore
RIEPILOGO
Gruppi
Analisi
Geometria
Algebra
Fisica
Conteggio
15
15
15
15
Somma
399
378
384
350
Media
26,6
25,2
25,6
23,33333
Varianza
2,542857
1,028571
1,542857
11,52381
ANALISI VARIANZA
Origine
della
variazione
Tra gruppi
In gruppi
SQ
gdl
MQ
84,05
232,9333
3
56
Totale
316,9833
59
28,01667
4,159524
Anche in tal caso le medie risultano diverse.
(e) La matrice di correlazione associata ai dati è
F
Valore di
significativit
à
6,735547
0,000584
F crit
2,769433
Analisi Geometria Algebra
Analisi
1
Geometria -0,25617
1
Algebra
0,562565 -0,49897
1
Fisica
0,277097 0,103735 -0,22022
Fisica
1
La sua decomposizione spettrale usando il MATLAB risulta
0.38
0.58
−0.5 −0.46
− 0.2
0.79
0.52 − 0.20
D = diag (1.89,1.21,0.64,0.24) P =
− 0.68
0.29
− 0.65 0.14
0.05 − 0.85 − 0.3527 − 0.38
Risulta che le prime due componenti principali coprono il 77% della variabilità totale e sono
pertanto sufficienti alla trasformazione del campione. Le prime due componenti principali sono
pertanto:
Y1 = −0.5 Analisi − 0.46Geometria + 0.38 Algebra + 0.58 Fisica
Y2 = 0.52 Analisi − 0.20Geometria + 0.79 Algebra − 0.2 Fisica
2. Il coefficiente di collasso è dato dalla funzione densità diviso la funzione di affidabilità, ossia:
1
1
Z (t ) = 100 =
, t ∈ [0,100]
t
100 − t
1−
100
3. Si tratta di applicare un test di Mc-Nemar poiché si tratta di dati appaiati (prima e dopo) e di
risposte binarie (è cambiato oppure no il consumo di cioccolata). Lo schema è il seguente:
prima
Totale
50
-50
dopo
50
35
10
45
-50
12
143
155
Totale
47
153
200
Il numero medio di variazioni è (10+12)/2=11. La statistica test è (12-11)^2/11+(10-11)^2/11=0.18.
Il quantile relativo a 0.05 è 3.84 pertanto non si possono ritenere imputabili alla caffeina assunta le
variazioni di consumo registrate.












