Università degli Studi dell`Insubria Facoltà di Scienze MM.FF.NN

Università degli Studi dell’Insubria
Facoltà di Scienze MM.FF.NN. /Como
Corso di laurea in Matematica, L-35 Scienze Matematiche
Nome Inglese del Corso: Mathematics
MANIFESTO DEGLI STUDI – ANNO ACCADEMICO 2012/2013
Presentazione
Durata normale del corso di studio: 3 anni.
Crediti Formativi Universitari (CFU) da acquisire per il conseguimento della laurea: 180.
Anni attivati 3
Numero di esami previsto: 20.
Titolo di studio rilasciato: Laurea in Matematica.
Il titolo di studio dà accesso, previa verifica delle conoscenze, al corso di Laurea Magistrale in Matematica, e ad altri
corsi di Laurea Magistrale che ammettano all’accesso studenti con un curriculum in Matematica.
Obiettivi formativi specifici
Il corso di laurea in matematica ha come principale obiettivo formativo quello di garantire un ampio ed equilibrato
bagaglio di strumenti e metodi matematici non disgiunto da un’ampia panoramica, in vari ambiti, delle loro
applicazioni; questo in modo da permettere al laureato sia l’approfondimento di strumenti e metodi con il
proseguimento degli studi con una laurea magistrale sia l’inserimento in attività professionali. In quest’ottica il corso
degli studi in Matematica si propone di fornire una solida base nelle discipline classiche della matematica
(analisi/geometria/algebra) per un periodo di circa 3 semestri e contemporaneamente di far acquisire le indispensabili
conoscenze in campo informatico. Il corso prosegue con l’introduzione di ulteriori discipline (fisica, analisi numerica,
statistica, economia, ecc) che permettono oltre all’ampliamento delle conoscenze anche concrete applicazioni delle
metodologie precedentemente acquisite. La personalizzazione del percorso di studio è resa possibile oltre che dai CFU a
scelta libera dello studente, anche da corsi a scelta vincolata. La modalità didattica è prevalentemente quella
tradizionale delle lezioni ed esercitazioni frontali, alle quali vengono affiancate attività di laboratorio, relative sia ai
corsi di informatica sia a quelli di discipline di natura modellistico-numerica. A completamento del percorso di
apprendimento, sono inoltre previste attività di natura seminariale, svolte dagli studenti sia in gruppo che singolarmente,
sotto la diretta supervisione dei docenti, in modo da sviluppare sia l'abilità di lavoro in gruppo sia le doti comunicative.
Tali attività si svolgono all’interno dei singoli insegnamenti, e concorrono alla valutazione finale del corso.
I risultati di apprendimento attesi, e di seguito espressi mediante i Descrittori europei, vengono in generale conseguiti
con corsi di lezioni frontali, esercitazioni a carattere teorico, esercitazioni di laboratorio di informatica e di matematica
computazionale. Vengono verificati con prove di esame scritte e orali, relazioni sull’attività svolta.
Risultati di apprendimento attesi, espressi tramite i Descrittori europei del titolo di studio
Conoscenza e capacità di comprensione (knowledge and understanding)
I laureati in Matematica:
a)conoscono e sanno utilizzare il calcolo differenziale ed integrale in una e più variabili e l'algebra lineare;
inoltre, posseggono le seguenti:
- conoscenze di base di fisica matematica;
- conoscenze di base di equazioni differenziali ordinarie e alla derivate parziali;
- conoscenze di base sul calcolo delle probabilità e sulla statistica matematica;
- conoscenze di base di analisi numerica e di calcolo scientifico;
- conoscenze di base sulla geometria di curve e superfici e e varietà differenziali astratte;
- conoscenze delle principali strutture algebriche;
- conoscenze di base di topologia generale e algebrica;
- conoscenze di base di analisi reale;
- conoscenze di base di fisica generale;
b) conoscono e comprendono le applicazioni di base della Matematica alla Fisica e all'Informatica;
c) hanno adeguate competenze computazionali e informatiche, comprendenti anche la conoscenza di linguaggi di
programmazione e di software specifici;
d) sono capaci di leggere e comprendere testi avanzati di Matematica anche in lingua inglese.
Gli studenti acquisiscono tali conoscenze mediante i corsi, comuni a tutti i percorsi di studio, in cui sono previste
lezioni, esercitazioni e attività di tutorato. In particolare sono previsti un corso di elementi di informatica e
programmazione, e almeno dodici crediti di fisica generale. Le conoscenze computazionali vengono fornite all'interno
dei corsi di natura modellistico numerica, che possono prevedere attività di laboratorio.
Le capacità di lettura e comprensione di testi scientifici si sviluppano inizialmente con lo studio dei testi di riferimento
per i singoli corsi, anche in lingua Inglese, e si approfondiscono durante il lavoro per la preparazione della prova finale.
Capacità di applicare conoscenza e comprensione (applying knowledge and understanding)
I laureati in matematica:
a) sono in grado di produrre dimostrazioni rigorose di risultati matematici non identici a quelli già conosciuti ma
chiaramente correlati a essi;
b) sono in grado di risolvere problemi di moderata difficoltà in diversi campi della matematica;
c) sono in grado di formalizzare matematicamente problemi di moderata difficoltà formulati nel linguaggio naturale, e
di trarre profitto da questa formulazione per chiarirli o risolverli;
d) sono in grado di estrarre informazioni qualitative da dati quantitativi;
e) sono in grado di utilizzare strumenti informatici e computazionali come supporto ai processi matematici, e per
acquisire ulteriori informazioni.
Le capacità sopra elencate vengono acquisite all'interno dei singoli corsi, molti dei quali prevedono esercitazioni nelle
quali lo studente affronta, con progressiva autonomia, problemi di crescente difficoltà. La capacità di estrarre
informazioni qualitative da dati quantitativi viene acquisita mediante corsi di indirizzo fisico o modellistico/applicativo,
comuni a tutti i percorsi di studio. Tali corsi possono prevedere l'uso di strumenti informatici e di software specifici.
Le capacità elencate vengono accertate mediante gli esami dei vari corsi, che sono spesso articolati in una prova scritta
ed una orale, e permettono di verificare il livello di autonomia raggiunto. A questa verifica contribuiscono inoltre
attività seminariali svolte dagli studenti all'interno dei singoli corsi sotto la supervisione dei docenti.
Autonomia di giudizio (making judgements)
I laureati in matematica:
a) sono in grado di costruire e sviluppare argomentazioni logiche con una chiara identificazione di assunti e
conclusioni;
b) sono in grado di riconoscere dimostrazioni corrette, e di individuare ragionamenti fallaci;
c) sono in grado di comprendere modelli matematici associati a situazioni concrete derivanti da altre discipline, e di
usare tali modelli per facilitare lo studio della situazione originale;
d) hanno esperienza di lavoro di gruppo, ma sanno anche lavorare bene autonomamente.
Le capacità elencate ai primi due punti sono sviluppate mediante tutte le attività previste dal corso di studio. La
modellizzazione matematica di problemi viene presentata in alcuni dei corsi obbligatori, in particolare quelli di natura
fisica e numerica. Queste capacità vengono accertate mediante gli esami e lo svolgimento di attività seminariali.
Le attività previste dal percorso formativo proposto sono in larga misura individuali. Tuttavia la collaborazione tra
studenti per la risoluzione di problemi assegnati durante le esercitazione e per la preparazione di progetti e seminari da
svolgersi nell'ambito dei corsi abituano gli studenti a lavorare in gruppo.
Abilità comunicative (communication skills)
I laureati in matematica:
a) sono in grado di comunicare problemi, idee e soluzioni riguardanti la Matematica, sia proprie sia di altri autori, a un
pubblico specializzato o generico, sia in forma scritta che orale;
b) sono in grado di dialogare con esperti di altri settori, riconoscendo la possibilità di formalizzare matematicamente
situazioni di interesse applicativo, industriale o finanziario.
Le capacità citate vengono acquisite mediante tutte le attività previste dal percorso formativo, e in particolare mediante
la preparazione per lo svolgimento di attività seminariali e della prova finale. Attività seminariali e prova finale sono
anche i principali mezzi tramite i quali tali capacità vengono accertate.
Capacità di apprendimento (learning skills)
I laureati in matematica:
a) sono in grado di proseguire gli studi, sia in Matematica che in altre discipline, con un alto grado di autonomia;
b) hanno una mentalità flessibile, e sono in grado di inserirsi prontamente negli ambienti di lavoro, adattandosi
facilmente a nuove problematiche.
Tutte le attività formative previste concorrono a fornire queste capacità, che costituiscono uno degli aspetti più
qualificanti e riconosciuti del laureato in Matematica.
Profili professionali e sbocchi occupazionali
Oltre che la prosecuzione degli studi con una laurea magistrale in Matematica e discipline affini (fisica, finanza, scienze
attuariali), il laureato triennale potrà trovare inserimento lavorativo in tutti quegli ambiti dove è richiesta una solida
formazione di base, l’attitudine al ragionamento e la capacità di chiarificare un problema facilitandone la soluzione,
mediante la sua formulazione in linguaggio matematico. Fra gli ambiti lavorativi in cui conoscenze e competenze
acquisite possono essere utilizzate sono compresi il supporto matematico e modellistica-applicativo ad attività
industriali, attività nella finanza, nei servizi, nella pubblica amministrazione e nella diffusione della cultura scientifica.
Il corso prepara alla professione di
•
2.1.1.3.1 -
Matematici
Ammissione al corso
Per essere ammesso al corso di laurea lo studente deve essere in possesso del diploma di scuola secondaria superiore
richiesto dalla normativa in vigore, o di altro titolo di studio conseguito all'estero, riconosciuto idoneo dagli organi
competenti dell'Università. Per l'ingresso si richiede inoltre che lo studente possieda una buona padronanza dei concetti
di base di aritmetica, algebra e geometria e che abbia attitudine al ragionamento logico-deduttivo ed alla risoluzione di
problemi. Ai sensi dell’art 6. D.M. 270/04 gli studenti dovranno sostenere una prova di verifica dell’adeguatezza della
preparazione iniziale. I test d’ingresso, che sono organizzati a livello nazionale, verranno offerti in due date prima
dell’inizio delle lezioni, indicativamente all’inizio ed alla fine di settembre. Una terza prova suppletiva riservata a
studenti che per motivi documentati non avranno potuto partecipare alle prove di Settembre sarà organizzata in
Dicembre. Per coloro che non dovessero superare il test sono previste, prima dell’inizio e durante lo svolgimento delle
lezioni, delle attività formative di recupero con ulteriore prova di verifica.
Nel caso in cui la verifica non risultasse ancora positiva non sarà inibita la possibilità di frequentare i corsi o sostenere
gli esami del primo anno, ma gli studenti dovranno seguire attività formative aggiuntive assegnate individualmente dal
Coniglio di Coordinamento Didattico al fine di acquisire le competenze entro il primo anno di corso. Le competenze
verranno considerate acquisite dagli studenti che avranno superato uno tra gli esami di Analisi Matematica I, Algebra
Lineare e Geometria o Algebra I. Per i dettagli sulle prove di verifica della preparazione iniziale, consultare il sito web
alla seguente pagina:
http://www.uninsubria.it/pls/uninsubria/consultazione.mostra_pagina?id_pagina=11588
Calendario delle attività didattiche
Le attività didattiche si svolgeranno nei seguenti periodi:
1oSEMESTRE
1 ottobre 2012 – 25 gennaio 2013
2oSEMESTRE
25 febbraio 2013 – 14 giugno 2013
Vacanze accademiche
FESTIVITA’
Natale
GIORNATE DI VACANZA ACCADEMICA
Dal 24.12.2012 al 04.01.2013 compresi
Pasqua
Dal 28.03.2013 al 02.04.2013 compresi
Appelli d’esame
Gli appelli d’esame si svolgono di norma nei periodi di pausa dell’attività didattica.
“Lo studente in regola con l’iscrizione ed i versamenti relativi può sostenere, senza alcuna limitazione numerica, tutti
gli esami e le prove di verifica per i quali possieda l’attestazione di frequenza, ove richiesta, che si riferiscano
comunque a corsi di insegnamento conclusi e nel rispetto delle eventuali propedeuticità.” (Ex Art.20 comma 3,
Regolamento Didattico di Ateneo).
Per poter sostenere l’esame gli studenti devono prenotarsi all’appello utilizzando la Bacheca on-line di Esse3
accessibile al seguente indirizzo: http://uninsubria.esse3.cineca.it
Le date degli appelli saranno rese note sul medesimo sito web.
Sessione unica degli esami di profitto
INIZIO
21 gennaio 2013
TERMINE
31 marzo 2014
Organizzazione del Corso di laurea
La durata normale del corso di laurea in Matematica è di tre anni. Per il conseguimento della laurea lo studente deve
acquisire 180 crediti formativi universitari (CFU).
L’apprendimento delle competenze e delle professionalità da parte degli studenti è computato in CFU, una misura del
lavoro di apprendimento richiesto allo studente. I CFU corrispondono ciascuno ad un carico standard di 25 ore di
attività, comprendenti:
• 8 ore di lezioni frontali con annesse 17 ore di studio individuale;
• 12 ore di esercitazioni con 14 ore di rielaborazione personale;
• 12 ore di laboratorio con 14 ore di rielaborazione personale;
• 25 ore di attività formative relative alla preparazione della prova finale.
La didattica è organizzata per ciascun anno di corso in due cicli coordinati, convenzionalmente chiamati semestri. Sono
previste lezioni frontali, esercitazioni pratiche, corsi di laboratorio.
La struttura e l’articolazione di ciascun insegnamento e delle altre attività formative, con l’indicazione di ogni elemento
utile per la relativa fruizione da parte degli studenti iscritti sono specificati annualmente nel Manifesto degli studi e
nella Guida dello studente.
I vari insegnamenti possono essere attivati direttamente o eventualmente mutuati da altri corsi di laurea della Facoltà e,
ove necessario, dell’Ateneo, nonché, sulla base di specifici accordi, di altri Atenei
L’acquisizione da parte dello studente dei crediti stabiliti per ciascun insegnamento è subordinata al superamento delle
relative prove d’esame, che danno luogo a votazione in trentesimi, salvo per la prova di lingua inglese di cui si parla
successivamente.
Le attività formative comprendono insegnamenti ripartiti, conformemente alla normativa vigente, in ambiti di base,
caratterizzanti, affini o integrativi e attività a scelta dello studente. Per i contenuti degli insegnamenti si rimanda alla
Guida dello Studente.
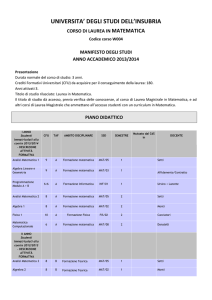
Di seguito sono riportate le attività formative per ciascun anno, riportando per ciascuna il numero di CFU ed il settore
scientifico-disciplinare (SSD).
Settore
scientifico Credit
Ambito disciplinare
disciplina
i
re
I ANNO Insegnamenti
Tipo di
attività
formativa
Docente
di base
Setti A.
I Semestre
Analisi Matematica I
MAT/05
9
Algebra Lineare e Geometria
MAT/03
9
INF/01
12
II Semestre
Analisi Matematica II
MAT/05
8
Algebra I
MAT/02
8
MAT/08
6
FIS/02
10
Formazione Fisica
62
di base
MAT/05
MAT/03
MAT/02
FIS/07
8
8
8
6
Formazione teorica
Formazione teorica
Formazione teorica
Affine-integrativo
caratterizzante
caratterizzante
caratterizzante
Affine-
Programmazione
Laboratorio
di
Computazionale
Matematica
Fisica I
TOTALE CREDITI
II ANNO Insegnamenti
I Semestre
Analisi matematica 3
Geometria 1
Algebra 2
Fisica 2
Formazione
matematica
Formazione
matematica
Formazione
informatica
Formazione
Matematica
Formazione
matematica
Formazione
matematica
di base
di base
di base
Setti A.
di base
di base
Setti A.
Benza V.
integrativo
II Semestre
Analisi numerica
MAT/08
8
Geometria 2
Probabilità e statistica
MAT/03
MAT/06
8
8
Corso a scelta
IIIANNO Insegnamenti
I Semestre
Un corso a scelta tra:
Sistemi dinamici
Formazione
modellisticoapplicativa
Formazione teorica
Formazione
modellisticoapplicativa
caratterizzante
Serra Capizzano S.
caratterizzante
caratterizzante
Casini E.
8
Art.10.Comma 5a
FIS/02
8
SECSS/01
MAT/07
8
8
Un corso a scelta tra:
Metodi Matematici della Fisica
FIS/02
8
Affineintegrativa
Metodi Formali in Informatica
MAT/08
8
Affineintegrativa
MAT/02
MAT/03
MAT/05
MAT/07
MAT/08
8
Formazione teorica
caratterizzante
8
Formazione
modellisticoapplicativa
caratterizzante
Statistica
e
all’Economia
Fisica matematica 1
Applicazioni
II Semestre
Un corso a scelta della Tabella A
Un corso a scelta della Tabella B
Corso a scelta
Altre
conoscenze
utili
per
l’inserimento nel mondo del lavoro
Prova finale
Tabella A (attività formativa teorica)
Istituzioni di analisi superiore Mod. MAT/05
A + Mod.B
Istituzioni di algebra superiore
MAT/02
Istituzioni di Geometria superiore
MAT/03
Guarneri I.
Posilicano A.
Vedi insegnamento “Metodi
Matematici della Fisica
Mod.1”
L Fisica
Guarneri I.
Vedi insegnamento “Metodi
numerici in informatica”
LM Matematica
8
1
Art.10.Comma 5a
Art.10.Comma 5d
5
Art.10.Comma 5c
4+4
Cazzaniga F.
8
Vedi insegnamento omonimo LM
Matematica
Carboni A.
Vedi
insegnamento
“Geometria
superiore” LM Matematica
8
Tabella B (attività formativa modellistico-applicativa)
Istituzioni di Fisica Matematica
MAT/07 8
Metodi Probabilistici in Fisica MAT/07 8
Matematica
Analisi numerica 2
MAT/08 8
- Attività formative a scelta dello studente
Formazione
modellisticoapplicativa
Affineintegrativa
Affineintegrativa
caratterizzante
Mantica G.
Posilicano A.
Sono riservati 16 CFU ad attività formative a scelta dello studente purché coerenti con il percorso formativo. Lo
studente, di norma, potrà scegliere insegnamenti nella lista di quelli caratterizzanti o affini e integrativi di questo Corso
di laurea. Alternativamente, lo studente può esprimere la scelta di un insegnamento non incluso in queste liste, anche in
altro Ateneo, e sottoporre questa proposta alla approvazione del Consiglio di coordinamento didattico. Gli studenti
possono acquisire i crediti relativi alle attività formative a scelta a partire dal secondo anno di corso. Questa norma si
estende anche agli studenti che si sono immatricolati nell’anno accademico 2011/2012.
- Lingua inglese
E’ richiesta l’acquisizione di 2 CFU in lingua inglese. L’acquisizione del credito avviene in seguito ad una prova
conoscenza della lingua. La prova di verifica della conoscenza linguistica può essere sostituita dalla presentazione di
certificati di riconosciuta validità internazionale.
- Modalità di verifica del profitto
Gli esami di profitto possono essere scritti e/o orali. Gli insegnamenti di laboratorio possono comprendere anche
verifiche pratiche.
I docenti possono prevedere forme articolate di accertamento del profitto, eventualmente composte di prove successive,
anche scritte, da concludere comunque con un controllo finale.
- Frequenza
La frequenza non è obbligatoria.
- Piani di studio
Il piano di studio è l’insieme delle attività formative obbligatorie e delle attività formative scelte autonomamente dallo
studente in coerenza con il regolamento didattico del corso di studio. Allo studente viene automaticamente attribuito un
piano di studio all’atto dell’iscrizione al primo anno, che costituisce il piano di studio statutario. All’inizio del I
semestre del II anno lo studente deve presentare un proprio piano di studio con l’indicazione delle attività a scelta. Il
piano di studio è approvato dal Consiglio di Coordinamento Didattico. Il diritto dello studente di sostenere prove di
verifica relative a una attività formativa è subordinato alla presenza dell’attività stessa nell’ultimo piano di studio
approvato. Per quanto non previsto si rinvia al regolamento d’Ateneo per gli studenti.
- Propedeuticità
Gli insegnamenti contrassegnati con I sono di propedeutici a quelli contrassegnati con II. L’insegnamento di Statistica e
Probabilita’ e’ propedeutico a quello di Statistica e applicazioni all’economia.
- Attività di orientamento e tutorato
Sono previste attività di tutorato a supporto dei corsi, qualora il docente ne riscontri l’esigenza.
- Appelli d'esame
Gli appelli d’esame si svolgono di norma nei periodi di pausa dell’attività didattica.
Prova finale
Per essere ammesso alla prova finale, lo studente deve aver acquisito almeno 175 CFU. I crediti associati alla
preparazione della prova finale, pari a 5 CFU, vengono riconosciuti al superamento di questa. La corrispondenza tra
l'ultimo piano di studio approvato e i crediti effettivamente conseguiti è condizione per l'ammissione alla prova finale.
La prova finale consiste nella redazione di una tesina di argomento monografico, concordato con un docente di
riferimento, nella quale lo studente deve principalmente mostrare, in un elaborato scritto, le sue autonome capacità di
comprensione e di sintesi.
Riconoscimento CFU e modalità di trasferimento
Trasferimento da altro Ateneo
In caso di trasferimento da altro Ateneo lo studente può chiedere il riconoscimento di crediti formativi acquisiti nel
precedente Corso di Studio. Il riconoscimento viene effettuato dal Consiglio di Coordinamento Didattico, sulla base
della conformità fra i contenuti del corso di provenienza e quelli del corso a cui si vuole accedere. E’ ammesso il
riconoscimento parziale di un insegnamento.
Per il riconoscimento delle attività di studio svolte all’estero e dei relativi CFU, si applica quanto disposto dal
Regolamento didattico di Ateneo.
Riconoscimento di attività professionali
Il numero massimo di crediti formativi universitari riconoscibili per attività professionali certificate
individualmente a sensi della normativa vigente (DM 16/3/2007 Art. 4) è fissato in 12.
Altre informazioni
Sede del Corso: Dipartimento di Scienza e Alta Tecnologia, Via Valleggio 11, 22100 Como, Italia
Presidente del Consiglio di Coordinamento Didattico in Matematica: prof. Alberto G. Setti
Referente didattico: prof. Alberto G. Setti
Segreteria didattica: telefono +39 031 3383201/2
URL del corso di laurea:
www.uninsubria.it/url/scico/l-mat
Per le procedure e termini di scadenza di Ateneo relativamente alle immatricolazioni, iscrizioni, trasferimenti,
presentazione dei Piani di studio consultare il sito web
www.uninsubria.it/web/segreterie
Per tutto quanto non previsto nel presente Manifesto si fa riferimento a quanto riportato nel Regolamento di Corso di
Studio.