CAPITOLO III. Configurazioni di equilibrio nei cristalli liquidi in

1
CAPITOLO III. Configurazioni di equilibrio nei cristalli liquidi in presenza di campi:
La soglia di Freederickz e la transizione di saturazione.
I- Alcune distorsioni importanti per i cristalli liquidi.
a) Distorsione di Twist.
z
.
.
.
.
.
.
.
.
.
.
y
vetrini
x
ϕ(z)
n
x
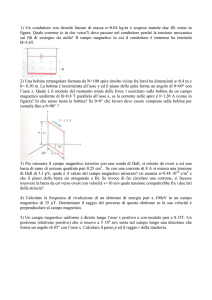
Figura1. Rappresentazione schematica di una distorsione di twist. Le bacchette indicano la proiezione del
direttore sul piano xz. Più corta è la bacchetta e più il direttore è inclinato rispetto al piano xz. I punti sulla
superficie in alto indicano un’orientazione del direttore ortogonale al piano xz.
Questa distorsione è quella mostrata in fig.1. In tale distorsione il direttore giace sempre
parallelo ad un dato piano xy formando con l’asse x un angolo ϕ(z) che dipende dalla sola
coordinata z (distorsione unidimensionale). Una tale distorsione si produce, ad esempio, se un
cristallo liquido è posto fra due vetrini paralleli trattati in modo da imporre un ancoraggio
planare omogeneo lungo due direzioni diverse sui due vetrini. In questa distorsione, il direttore
è
rappresentato da
(1)
n = (cosϕ ( z),sin ϕ ( z), 0)
La densità di energia elastica è:
K
K
K
2
2
2
(2)
Fel = 1 ( divn) + 2 (n • rotn) + 3 (n × rotn)
2
2
2
Utilizzando la (1) si trova:
∂n ∂n ∂n
divn = x + y + z = 0
∂x ∂y ∂z
∂n ∂n
dϕ
rotnx = z − y = − cosϕ ( z)
∂y ∂z
dz
dϕ
∂n x ∂n z
rotny =
−
= − sin ϕ ( z)
dz
∂z ∂x
∂n y ∂n x
rotnz =
−
=0
∂x ∂y
Dunque,
dϕ ( z )
rotn = −
n
dz
In conclusione, divn = 0, n × rotn = 0 in eq.(2). Dunque, l’unico contributo in eq.(2) che è
dϕ
diverso da zero è quello di twist essendo n • rotn = −
. Sostituendo tali valori nella (2) si
dz
trova:
2
1  dϕ 
Fel = K 2
(3)
2  dz 
2
Che rappresenta l’espressione generale della densità di energia per una deformazione di puro
twist. In questo caso, il contributo elastico di superficie ( K24 in eq.(21) cap.II) è nullo e l’unica
interazione di superficie è quella di ancoraggio.
b) Distorsione di splay-bend.
In questo caso, il direttore n resta sempre parallelo ad un dato piano xz e varia solo in funzione
di z, come mostrato schematicamente in Fig.2. Anche questa è una deformazione
unidimensionale perchè dipende dalla sola coordinata z ed è planare perchè n resta sempre in
uno stesso piano (piano xz).
z
z
n
θ(z
)
x
Figura 2. Distorsione di splay-bend.
Se indichiamo con θ(z) l’angolo formato con l’asse x, l’espressione del direttore diventa:
(4)
n = (cosθ ( z), 0,sin θ ( z))
In tal caso, si trova immediatamente che il contributo di twist è n • rotn = 0 , dunque solamente i
contributi di splay e di bend sono diversi da zero. Svolgendo i calcoli si ottiene facilmente:
2
1
 dθ 
Fel = (K1 cos2 θ + K 3 sin 2 θ )
(5)
 dz 
2
Anche in questo caso, il contributo elastico di superficie ( K24 in eq.(21) cap.II) è nullo e l’unica
interazione di superficie è quella di ancoraggio. L’espressione (5) è simile a quella valida per
il twist ( eq.(3)) con la differenza che adesso, al posto della costante di twist K 2, compare la
costante elastica efficace di splay-bend
(6)
K (θ ) = K1 cos2 θ + K 3 sin 2 θ ,
che dipende dall’angolo θ. Per θ =0 , K(θ) coincide con K1 mentre si riduce a K3 per θ =90°.
In effetti, se si osserva la figura 2, si riconosce immediatamente che la distorsione è di tipo
splay nei pressi della superficie superiore dove θ =0, mentre è di tipo bend nei pressi della
superficie inferiore dove θ =90°. Il fatto che la configurazione di splay bend è caratterizzata da
una costante elastica efficace che dipende dall’orientazione del direttore rende più complesso lo
studio di tali configurazioni rispetto a quelle di twist. Tuttavia, nella maggior parte dei cristalli
liquidi le costanti K1 e K3 hanno valori confrontabili ( le differenze fra i valori sono minori del
25%). Ne consegue che un’approssimazione ragionevole consiste nel rimpiazzare la costante
elastica K(θ ) con un valore costante K =(K 1+K3)/2 pari al valor medio fra K1 e K 3 . Questa
approssimazione, detta approssimazione ad una costante, permette di ridurre notevolmente la
difficoltà dei calcoli.
II- Il passo dei Colesterici.
Come abbiamo visto, per i colesterici, la mancanza della simmetria di inversione spaziale
aggiunge un contributo elastico lineare in n • rotn nella densità di energia elastica(vedi eq.(21)
cap II) che è dipendente dalla costante elastica Kc che ha le dimensioni di una forza diviso una
lunghezza (N/m) e può essere sia positiva che negativa.
3
K1
K
K
(7)
(divn) 2 + 2 (n • rotn) 2 + 3 (n × rotn) 2
2
2
2
Si può dimostrare facilmente che tale contributo favorisce la nascita di una deformazione di
puro twist. Infatti, come visto sopra, in una configurazione di twist valgono le uguaglianze
dϕ
. Sostituendo tali valori nella densità di energia libera
divn = 0, n × rotn = 0 e n • rotn = −
dz
in eq. (7), si trova:
2
dϕ K 2  dϕ 
Fel = −K c
+
(8)
dz
2  dz 
Come vedremo nel seguito, l’energia libera totale del cristallo liquido risulta minimizzata se il
twist è uniforme e, cioè se dϕ/dz = q =costante. Dunque, per i calcoli successivi, ci restringiamo
a considerare il caso di un twist uniforme in cui ϕ(z) = qz =2πz/p, dove p è il passo del
colesterico. Sostituendo tale espressione nella densità di energia libera in eq.(8) si ottiene:
K
(9)
Fel = −K c q + 2 q 2
2
L’energia libera totale è data da F =Fel V, dove V è il volume occupato dal cristallo liquido
(vedi fig.3).
Fel = K c (n • rotn) +
Figura 3. Energia libera totale di un colesterico in funzione della velocità di twist q.
Si vede chiaramente che un’orientazione uniforme del direttore (q =dϕ/dz=0) non rende minima
l’energia libera, mentre esiste una ben precisa distorsione di twist con q = q0 ≠0 che minimizza
l’energia . Imponendo la condizione dF/dq=0 si trova
K
q = q0 = c
(10)
−K c + K 2q = 0
K2
Dunque, a causa della costante Kc, la configurazione di equilibrio dei colesterici è caratterizzata
da un twist uniforme. Il valore e il segno di Kc determinano, rispettivamente, il valore del
passo di equilibrio dell’elica colesterica (p =2π/q0) e il senso di rotazione dell’elica.
⇒
III- Riorientazione di cristalli liquidi in campi magnetici ed elettrici: l’approssimazione di
nematico semiinfinito.
Adesso vediamo cosa accade se applichiamo un campo magnetico ( o un campo elettrico) ad
un cristallo liquido nematico. Consideriamo, ad esempio, il caso di un cristallo liquido
contenuto fra due piastre piane e parallele che si trovano a distanza d come mostrato
schematicamente in fig. 4. Le piastre sono trattate in modo da indurre un ancoraggio lungo un
asse x nel piano. Un campo magnetico H può essere applicato lungo l’asse y ortogonale
all’asse facile nel piano delle piastre. Si avrà , quindi, una competizione fra i momenti
superficiali di ancoraggio che tendono a mantenere il direttore orientato lungo gli assi facili
sulle superfici e il campo che tende a farlo ruotare verso l’asse y.
4
z
H
x
Figura 4.
In condizioni di equilibrio, ci si aspetta, perciò, che sia presente una distorsione spaziale del
direttore. Data la simmetria del problema, la distorsione sarà di twist cioè del tipo:
(11)
n = (cosϕ ( z),sin ϕ ( z), 0)
dove ϕ(z) è l’angolo che il direttore forma con l’asse x nel piano xy delle piastre. La densità
volumetrica di energia libera (elastica + magnetica) è:
2
1  dϕ  ∆χ m
−
Fv = Fel + Fm = K 2
µ0 H 2 sin 2 ϕ
(12)
2  dz 
2
Si ha, perciò, una competizione fra il contributo magnetico che tende ad allineare il direttore
lungo il campo, quello elastico che si oppone ad una distorsione del direttore e quello di
ancoraggio che tende a mantenere il direttore orientato lungo l’asse facile. Il problema generale
da risolvere è quello di trovare quale funzione ϕ(z) è tale da rendere minima l’energia libera
totale che è la somma dell’energia di volume e di quella di superficie (ancoraggio), cioè
F = ∫ ( Fel + Fm )dV + ∫ WdS
(13)
dove gli integrali sono fatti, rispettivamente, nel volume e sulle superfici delle piastre. Dato
che ϕ non dipende nè da x nè da y, la (13) diventa:
 d  1  dϕ  2 ∆χ


(14)
− m µ0 H 2 sin 2 ϕ dz + W1 (ϕ1 ) + W 2 (ϕ 2 ) 
F = S ∫  K 2


dz
2
2
0

 

dove S è la superficie delle piastre, W1 e W 2 sono le energie di ancoraggio sulle due piastre e
ϕ1=ϕ(0) e ϕ2=ϕ(d) sono gli angoli del direttore sulle due piastre. Per trovare la funzione ϕ(z)
che rende minima F, si usa il noto metodo di Eulero –Lagrange che riassumo, nel seguito, per
completezza. Sia ϕo(z) la funzione che minimizza F; sia inoltre η(z) una funzione arbitraria ed
α un piccolo coefficiente. L’energia libera corrispondente alla distorsione
(15)
ϕ ( z) = ϕ o ( z) + αη( z)
sarà una funzione di α che deve avere il suo minimo per α =0. Ciò significa che la
configurazione di equilibrio si potrà ottenere imponendo la condizione dF
che deve
dα α = 0 = 0
essere valida per qualunque valore della funzione η(z). Sostituendo ϕ(z) di eq.(15) nella (14) e
imponendo la condizione dF
= 0 si trova:
dα α = 0
d
1 dF
dW1
dW 2
 dϕ dη

= ∫ K2 o
− ∆χ m µ0 H 2 sin ϕ o cosϕ oη( z) dz +
η(0) +
η( d ) = 0
(16)

S dα α = 0 0 
dz dz
dϕ1
dϕ 2
Il primo termine nell’integrale può esssere integrato per parti e la (16) diventa
d


d 2ϕ o

−
K
∫  2 dz 2 − ∆χ mµ0H 2 sinϕ o cosϕ o η(z)dz
0
dϕ
dϕ
dW1
dW 2
+K 2 o η( d ) − K 2 o η(0) +
η(0) +
η( d ) = 0
(17)
dz z= d
dz z= 0
dϕ1
dϕ 2
Ora, si deve ricordare che la funzione η(z) è una funzione arbitraria. Dunque, l’unica
possibilità perchè valga l’uguaglianza a zero in eq.(17) per qualunque funzione η(z) è che i
termini che moltiplicano η(z), η(0) e η(d) siano ciascuno nullo cioè la funzione ϕo(z) dovrà
soddisfare in ogni punto l’equazione differenziale di Eulero-Lagrange
5
d 2ϕ o
(18)
+ ∆χ m µ0 H 2 sin ϕ o cosϕ o = 0
dz 2
con le condizioni al contorno sulle due superfici
dϕ
dW 2
−K 2 o
−
=0
(19)
dz z= d dϕ 2
dϕ
dW1
+K 2 o
−
=0
(20)
dz z= 0 dϕ1
Se gli ancoraggi sulle due superfici sono uguali con asse facile ϕf=0, si può scrivere:
W1= [W0 sin2(ϕ1)]/2 e W2=[W0 sin2(ϕ2)]/2
(21)
Queste equazioni hanno una semplice interpretazione fisica. Il primo termine nel membro a
sinistra in eq.(18) rappresenta il momento di forza elastico per unità di volume che si genera a
causa della distorsione elastica ( è l’analogo della forza elastica per unità di volume in un
mezzo elastico deformato), il secondo termine rappresenta, invece il momento di forza per
unità di volume esercitato dal campo magnetico già introdotto in precedenza (Γm in eq.(14)
capitolo II). Dunque, l’eq.(18) stabilisce che, all’equilibrio, il momento di forza totale
(elastico+magnetico) agente in ogni volumetto infinitesimo del cristallo liquido deve essere
nullo. Analogamente, le condizioni al contorno stabiliscono che all’equilibrio devono
annullarsi i momenti di forza agenti sulle due superfici. I primi contributi nelle equazioni (19)
e (20) rappresentano i momenti di forza elastici per unità di superficie mentre i secondi
termini rappresentano i momenti di forza di ancoraggio (eq.(18,19) del capitolo II). Un caso
particolarmente semplice si verifica quando l’ancoraggio è molto forte. In tal caso, il direttore
sulle due superfici resta praticamente allineato lungo gli assi facili (ϕf=0 in questa geometria).
Dunque, le condizioni al contorno nelle equazioni (19) e (20) possono essere sostituite con le
due condizioni più semplici
ϕ1 = 0 e ϕ2 = 0
(22)
Equazioni del tipo di eq.(18) si trovano spesso quando si studiano le distorsioni di equilibrio
nei cristalli liquidi. Un utile metodo di soluzione consiste nel moltiplicare entrambi i membri
dell’equazione per dϕo/dz ottenendo:
d 2ϕ o dϕ o
dϕ
(23)
K2
+ ∆χ m µ0 H 2 sin ϕ o cosϕ o o = 0
2
dz dz
dz
Si verifica facilmente che la (23) è uguale a:
2

1 d   dϕ o 
(24)
− ∆χ m µ0 H 2 cos2 ϕ o  = 0
K2

2 dz   dz 

K2
La cui soluzione generale è
2
 dϕ o 
− ∆χ m µ0 H 2 cos2 ϕ o = costante
K2
(25)
 dz 
data la simmetria del sistema ( uguali ancoraggi sulle due superfici), la funzione ϕ o(z) che
risolve l’equazione (25) deve essere una funzione simmetrica rispetto al centro z =d/2 della
cella. Dunque dϕo/dz = 0 al centro dove ϕ o deve raggiungere il valore massimo ϕmax.
Sostituendo tali valori (dϕo/dz=0 e ϕo= ϕmax) in eq.(25) si trova costante= −∆χ m µ0 H 2 cos2 ϕ o ,
dunque la (25) diventa:
2
dϕ
∆χ m µ0 2
 dϕ o 
= ∆χ m µ0 H 2 (cos2 ϕ o − cos2 ϕ max ) ⇒ o = ±
K2
H (cos2 ϕ o − cos2 ϕ max ) (26)
 dz 
dz
K2
I due segni + e – corrispondono a due possibili soluzioni equivalenti con twist orario o
antiorario. Infatti, in assenza di campo, il direttore è orientato dovunque uniformemente
lungo l’asse imposto dalle superfici. Quando si accende il campo magnetico lungo l’asse y
ortogonale al direttore, il momento di forza magnetico applicato sul direttore
6
Γm = ∆χ m µ0 H 2 sin ϕ o cosϕ o è nullo e questa orientazione corrisponde ad una posizione di
massimo per l’energia magnetica cioè ad una posizione di equilibrio instabile. In tal caso,
perchè il direttore possa orientarsi nel verso del campo ( o in verso opposto) è necessario che
, a causa di una fluttuazione termica iniziale, ϕo diventi diverso da zero. Se il valore iniziale
di ϕo è positivo, allora il momento di forza magnetico è positivo e il direttore tende a ruotare
nel verso del campo magnetico fino a portarsi in una configurazione di equilibrio
caratterizzata da un twist antiorario. Nel caso opposto il twist è orario. Questa situazione è
mostrata schematicamente in figura 5.
Figura 5a
Figura 5b
Ovviamente, questa degenerazione si presenta solamente se il campo è esattamente
perpendicolare all’asse facile. In caso contrario, il momento di forza applicato inizialmente
sul direttore ha un segno ben definito e il direttore ruota in un verso ben definito. Nel seguito
considereremo sempre la soluzione corrispondente al segno + in equazione (26) che
corrisponde al caso rappresentato in figura 5 a.
Un caso particolarmente semplice ed importante si verifica quando lo spessore del
campione è molto grande ( vedremo nel seguito cosa significa “molto grande”). In tal caso, ci
si aspetta che lontano dalle pareti, nella regione centrale della cella, il direttore si orienti
parallelamente al campo. Dunque, si può porre ϕmax=π/2 in eq.(26) e si ottiene l’equazione (
scegliendo la soluzione con il segno +):
cosϕ o
dϕ o
=+
(27)
dz
ξH
dove abbiamo definito la lunghezza di coerenza magnetica:
K2 1
(28)
ξH =
∆χ m µ0 H
Questa lunghezza diminuisce all’aumentare di H in modo inversamente proporzionale al
campo magnetico H. Per i cristalli liquidi nematici calamitici usuali come il 5CB, ξH ≈ 2-3
µm per un campo di induzione magnetica B= µ 0H di 1 T. L’equazione (27) si integra
facilmente usando il metodo delle variabili separabili:
ϕ
dϕ o
1 z
z
(29)
=+
dz =
∫ cos
∫
ϕo
ξH 0
ξH
ϕ1
la cui soluzione è:
 π / 2 − ϕ ( z) 
 π / 2 − ϕ1   z 
(30)
tan
exp− 
= tan



  ξH 
2
2
da cui si ricava immediatamente la funzione ϕ (z). Questa soluzione è mostrata
schematicamente in fig.6 in funzione di z/ξH.
7
Figura 6. Andamento dell’angolo del direttore vicino alla parete z = 0 nel caso in cui l’angolo in superficie è
ϕ1=15 °.
Come si vede, per z =0 l’angolo del direttore è ϕ1, e cresce esponenzialmente all’aumentare
della distanza dalla piastra finchè, per z >>ξH ( è sufficiente z ≈ 3 ξH) l’angolo è praticamente
coincidente con π/2 che corrisponde ad un’orientazione completa lungo il campo. Dunque, la
lunghezza di coerenza magnetica rappresenta la lunghezza caratteristica dello strato distorto
interfacciale in cui il direttore passa dall’orientazione di superficie a quella di volume. La
soluzione di eq.(30) è stata ottenuta facendo l’ipotesi che l’angolo al centro della cella (z
=d/2) sia praticamente coincidente con π/2. Questa soluzione, perciò, approssima molto bene
la soluzione esatta dell’equazione (26) solamente se effettivamente ϕ(d/2)≈ π/2 cioè d/2 > 3
ξH. Ricordando che, per B ≈1 T, ξH ≈ 2 µm ne deduciamo che, con tale campo, tale soluzione
è praticamente “esatta” se lo spessore d della cella è maggiore di 6 ξ H ≈ 12 µm. Questa
soluzione approssimata è nota con il nome di approssimazione di campione semiinfinito.
z
z
H
x
a
x
H
b
Figura7. Configurazioni di splay-bend.
La distorsione precedente era stata ottenuta nel caso particolare in cui l’asse facile e il
campo magnetico giacciono entrambi nel piano delle piastre e, perciò, la deformazione di
equilibrio è quella di twist. Nelle geometrie di figure 7a e 7b, invece, il campo magnetico
tende a far ruotare le molecole nel piano xz ortogonale alle piastre e contenente il campo H e
l’asse facile. La deformazione è, quindi di splay-bend ed è individuata dall’angolo θ(z) che il
direttore forma con l’asse z perpendicolare alle piastre. La densità di energia elastica
associata è
2
1
 dθ 
Fel = K (θ )
(31)
 dz 
2
dove K(θ) è la costante di splay-bend definita in eq.(6). In questo caso, dato che la costante
elastica dipende da θ , la minimizzazione dell’energia libera porta a espressioni un pò più
complicate per la funzione θ(z) di equilibrio ma qualitativamente dello stesso tipo trovato in
precedenza. In particolare, il direttore ruota gradualmente nel passare dalla superficie al
volume con una lunghezza caratteristica che è ancora del tipo di quella in eq.(28) ma dove al
posto di K2 compare una qualche costante elastica media di splay-bend. Nell’ipotesi
8
semplificativa di costanti elastiche isotrope ( K1=K3=K), la costante di splay bend si riduce a
K(θ ) =K e il problema si riduce formalmente allo stesso problema di twist purchè si
sostituisca in tutte le espressioni precedenti K2 con K e ϕ con θ.
IV- La soglia di Freederickz.
La discussione precedente valeva quando il campo magnetico è sufficientemente alto di modo
che ξH < d/6. Nel caso più generale, il momento di forza esercitato dal campo non è
sufficiente ad orientare completamente il direttore lungo il campo al centro della cella. Ne
consegue che ϕmax ≠ π/2 e la distorsione di equilibrio deve risolvere l’eq.(26). E’ importante
osservare che ϕo=ϕmax=0 rappresenta sempre una possibile soluzione dell’eq.(26). Infatti, se
il direttore resta dovunque orientato parallelamente all’asse facile, il momento di forza
magnetico è nullo insieme al momento di forza elastico e al momento di forza di ancoraggio.
Dunque, la situazione in cui il direttore resta dovunque orientato uniformemente lungo l’asse
facile rappresenta una soluzione stazionaria ( massimo o minimo dell’energia libera totale).
Per ottenere un’altra possibile soluzione distorta, si utilizza il metodo di separazione delle
variabili e si integra la (26) ottenendo:
ϕ
dϕ o
1
(32)
=+
z
∫
2
2
ξH
cos ϕ o − cos ϕ max
ϕ1
L’eq. (32) permette di calcolare ϕo(z) se è noto ϕmax. D’alta parte, ϕmax rappresenta l’angolo al
centro della cella, cioè il valore ϕ (d/2), quindi tale valore si può ottenere risolvendo
l’equazione implicita:
ϕ max
dϕ o
d
(33)
=+
∫
2
2
2ξ H
cos ϕ o − cos ϕ max
ϕ1
Ora consideriamo il caso di ancoraggio forte in cui ϕ1=0. Facendo la sostituzione
m =sin2 (ϕ max) e t =sin ϕo/sin ϕmax , l’integrale a sinistra si riduce all’integrale ellittico di
prima specie K(m) che rappresenta una funzione di m ben nota e definita da:
1
dt
K ( m) = ∫
(34)
2
1 − t 1 − mt 2
0
La funzione K(m) è una funzione crescente di m ( m >0) che assume il minimo valore
K(m)=π/2 per m =0. Ne consegue che l’equazione K(m)= d/2ξH ammetterà una soluzione
corrispondente ad un ben preciso valore di m ( m=sin2 (ϕmax) >0 ) solo se d/2ξH > π/2, cioè se
K2
π
(35)
d ∆χ m µ0
dove H c è detto campo di soglia di Freederickz. Per H <H c l’unica soluzione che risolve
l’equazione di Eulero-Lagrange è la soluzione corrispondente ad una orientazione del
direttore dovunque parallela agli assi facili. In tal caso, si può dimostrare che tale soluzione
corrisponde effettivamente ad un minimo dell’energia libera totale. Per H >Hc le soluzioni
stazionarie possibili sono 2, la prima è quella indistorta e la seconda è quella che corrisponde
ad un angolo al centro diverso da zero tale che m =sin2 (ϕ max) è soluzione dell’equazione
K(m)= d/2ξH. Con calcoli noiosi si può dimostrare che, in questo caso, la prima soluzione
diventa instabile ( corrisponde ad un massimo dell’energia libera) mentre la seconda
rappresenta effettivamente un minimo per l’energia libera. Dunque ad H =Hc si ha una
biforcazione ed una vera e propria transizione orientazionale dallo stato indistorto ad uno stato
distorto. Si può dimostrare, inoltre che per H di poco superiore ad Hc, l’angolo del direttore al
centro cresce rapidamente secondo una legge a potenza del tipo: ϕmax=a(H2-Hc2)1/2, dove a è
una costante moltiplicativa. L’andamento di ϕmax in funzione di H/Hc è mostrato
H > Hc =
9
schematicamente in figura 8a, mentre l’andamento di ϕo(z) in funzione di z per vari valori di
H è mostrato schematicamente in fig.8b.
a)
b)
Figura 8. a) angolo massimo in funzione di H/Hc; b) andamento dell’angolo nello spazio fra le due superfici z
=0 e z =d per vari campi magnetici.
L’esistenza di una soglia è dovuta al fatto che l’orientazione iniziale del direttore è
esattamente perpendicolare al campo. In queste condizioni speciali non c’è momento di forza
magnetico se il direttore resta orientato dovunque lungo tale direzione. Dunque tale
configuazione è una configurazione stazionaria che può essere sia di equilibrio stabile (H
<Hc) che di equilibrio instabile (H >Hc). Se , invece, il campo è orientato lungo una direzione
che fa un angolo diverso da π/2 con l’asse facile, la configurazione indistorta non potrà essere
mai di equilibrio perchè su di essa il campo magnetico esercita sempre un momento orientante
diverso da zero ( vedi eq.(14) cap.II). In tal caso, non c’è più una soglia e, per qualunque
valore del campo, si ha una distorsione orientazionale.
Analoghi fenomeni si osservano se si utilizzano le geometrie sperimentali mostrate
nelle figure 7a e 7b. Anche in questo caso si osserva una distorsione solamente quando il
campo è superiore ad un dato valore critico. Per valori di H di poco superiori al valore critico,
il direttore si sposta di poco rispetto all’orientazione imposta dagli assi facili e, quindi, θ ≈ 0
nel caso di fig.7a e θ ≈ π/2 nel caso di fig.7b. Ne consegue che nei due casi, la costante
elastica di splay-bend definita in eq.(6) si riduce, rispettivamente, alla costante di splay K1 e a
quella di bend K3. In tali condizioni, la distorsione corrispondente alla geometria di fig.7a è
praticamente indistinguibile da un puro splay, mentre quella in figura 7b è praticamente
indistinguibile da un puro bend. Ne consegue che i valori critici del campo per queste 2
geometrie si ottengono sostituendo, rispettivamente K1 e K3 al posto di K2 nella (35), cioè:
K1
K3
π
π
e
(36)
H ca =
H cb =
d ∆χ m µ0
d ∆χ m µ0
Dunque, misurando il campo di soglia di Freederickz per la geometria di twist e per quelle di
splay e di bend nelle figure 7, si possono ottenere i valori delle tre costanti elastiche. La
determinazione sperimentale della soglia di Freederickz nelle tre geometrie (twist, splay e
bend) rappresenta, in effetti, uno dei metodi più accurati per la misura delle costanti elastiche
dei cristalli liquidi se è nota l’anisotropia diamagnetica del cristallo liquido.
V- Effetti dei campi elettrici.
Effetti del tutto simili si hanno quando, al posto di un campo magnetico, si utilizza un
campo elettrico a.c. di ampiezza Eo e di frequenza sufficientemente elevata (ν > 1kHz). In
queste condizioni, come abbiamo visto in precedenza, gli effetti dovuti alle cariche elettriche
ioniche e alla flessoelettricità sono del tutto trascurabili e il sistema si comporta come se fosse
sottoposto solamente al momento di forza dielettrico prodotto da un campo statico equivalente
pari al valore efficace E=Eo/ 2 . Data la stretta analogia fra il momento di forza magnetico e
quello dielettrico, gli effetti prodotti da tale campo E sono sostanzialmente analoghi a quelli
prodotti dal campo magnetico H purchè si faccia la sostituzione in tutte le espressioni di ∆χm
10
con ∆ε , di µ0 con ε0 , e di H con E. In realtà, questa identità non è proprio esatta perchè,
mentre nel caso magnetico si può assumere che H sia costante in ogni punto, nel caso elettrico
E diventa una funzione di z da determinare. Infatti, in questo caso, il cristallo liquido viene
inserito fra due piastre piane con le superfici interne (quelle a contatto con il cristallo liquido)
su cui è depositato un sottile strato metallico. Una d.d.p. V viene applicata fra le due superfici
conduttrici. L’andamento del campo elettrico all’interno del condensatore piano si ottiene
risolvendo le corrispondenti equazioni di Maxwell con la condizione che la d.d.p. sia uguale a
V. Nel caso in cui l’orientazione del direttore non è uniforme, il campo elettrico non è
uniforme ma dipende dalla distanza z da una piastra. Questo fatto porta ad alcune
complicazioni nel calcolo della esatta distorsione di equilibrio per valori dei campi
apprezzabilmente superiori al valore di soglia ma non modifica gli aspetti qualitativi del
problema. In particolare, la distorsione del direttore è ancora caratterizzata da una lunghezza
caratteristica ( lunghezza di coerenza elettrica) che è pari a:
K 1
(37)
ξH =
∆εε0 E
dove K è una tipica costante elastica. Si noti che, in materiali come il 5CB, l’anisotropia
dielettrica è positiva e molto alta (∆ε ≈ 15). Con i massimi campi applicabili ( E ≈ 10 V/µm =
107 V/m) si possono raggiungere lunghezze di distorsione molto piccole (< 0.1 µm) che
potrebbero essere ottenute solamente con campi magnetici di enorme intensità ( B ≈ 100 T).
Una notevole semplificazione si ha nel caso del calcolo delle soglie di Freederickz. Infatti, per
campi di appena superiori alla soglia ( nel limite di E che tende ad Ec), il direttore resta
praticamente orientato uniformemente lungo la direzione iniziale. Ne consegue che la costante
elastica e il campo elettrico hanno dovunque lo stesso valore. Dunque, i valori dei campi
elettrici critici di Freederickz sono dati esattamente dalle relazioni che si ottengono
utilizzando le equazioni (35) e (36) e effettuando le sostituzioni precedentemente suggerite fra
le costanti magnetiche e quelle elettriche. E’ importante rilevare che il campo elettrico critico
risulta inversamente proporzionale allo spessore ( vedi eq.(35)). Dunque, La tensione elettrica
critica Vc=Ecd risulta indipendente dallo spessore della cella e dipende solamente dalle
costanti caratteristiche del cristallo liquido. In particolare, la tensione critica per il 5CB è di
circa 0.5 V qualunque sia lo spessore della cella. La soglia di Freederickz è, quindi, una soglia
in tensione e non in campo.
E’ importante osservare che molti materiali hanno una anisotropia dielettrica negativa
( ad esempio il CL MBBA). In tal caso, il campo elettrico tende ad orientarli lungo una
direzione perpendicolare al campo e non lungo la direzione parallela al campo. Ne consegue
che, in questo caso, le geometrie sperimentali che si debbono utilizzare per osservare la
transizione di Freederickz sono diverse dalle precedenti. Ad esempio, nel caso di una cella in
cui il direttore sia inizialmente perpendicolare alle pareti della cella ( configurazione
omeotropica), si potrà osservare la transizione solamente se il campo è parallelo
all’orientazione del direttore al contrario di quanto avveniva nel caso precedente in cui il
campo doveva essere perpendicolare al direttore.
VI- Effetti di un ancoraggio finito.
I risultati precedenti sono stati ottenuti assumendo ancoraggio molto forte e, cioè, che
il direttore sulle due superfici resti sempre orientato lungo l’asse facile (ϕ 1 =0). Se
l’ancoraggio non è molto forte, il momento di forza elastico agente sul direttore in superficie (
primo contributo in eq.(20) ) tende a far ruotare il direttore in superficie lungo la direzione del
campo. All’equilibrio il momento elastico è bilanciato dal momento di forza di ancoraggio
(vedi eq.(20)). In questo caso, per trovare la distorsione di equilibrio si deve utilizzare
l’equazione di volume (33) con la condizione al contorno (20). I calcoli sono piuttosto tediosi
e qui riporteremo solamente i risultati. Anche in questo caso si trova che c’è un campo critico
11
di soglia H*c ma questo è più piccolo di quello previsto nel caso di ancoraggio forte( eq.(35)).
Il valore del campo critico è legato a quello per ancoraggio forte (H c ) dalla semplice
relazione:
 2L 
H c * = H c 1 − est
(38)

d 
Dove Lest rappresenta la lunghezza di estrapolazione per una deformazione di twist definita
da:
K
Lest = 22
(39)
Wo
dove Wo è il coefficiente di ancoraggio. L’espressione (38) vale per Lest << d. La lunghezza di
estrapolazione rappresenta un parametro superficiale molto importante che varia normalmente
fra 10 nm nel caso di ancoraggio molto forte fino a 10 µm nel caso di ancoraggio
estremamente debole. Il significato fisico di Lest si può comprendere osservando l’andamento
dell’angolo ϕ(z) del direttore vicino alla superficie z = 0 in presenza di un campo magnetico
maggiore della soglia di Freederickz come mostrato in figura 9.
Figura 9. Confronto fra gli angoli del direttore vicino alla superficie z =0 nel caso di ancoraggio forte e in quello
di ancoraggio debole. La linea punteggiata rappresenta l’estrapolazione lineare della curva di ancoraggio debole
per z <0. Tale linea interseca l’asse orizzontale quando z = -Lest.
Come visto in precedenza, in queste condizioni il direttore ruota gradualmente nella direzione
del campo partendo dall’angolo superficiale ϕ 1. Come è evidente dalla figura, la curva
corrispondente ad un ancoraggio debole ( ϕ 1=25°) può essere “estrapolata” nella regione
esterna alla piastra (linea punteggiata per z < 0) ed incontra l’asse delle ordinate se z = - Lest.
Dunque, tutto avviene come se vi fosse una superficie “virtuale” posta in z = -Lest dove
l’ancoraggio è forte (ϕ1=0). Infatti in z = -Lest il valore individuato dalla linea punteggiata è
ϕ =0. Con questa osservazione si comprende perchè il campo di soglia in presenza di
ancoraggio debole è dato dalla (38) per Lest << d. Infatti, per quanto detto sopra, un cristallo
liquido posto fra due piastre poste a distanza d con lunghezza di estrapolazione Lest è del tutto
equivalente ad un cristallo liquido posto fra due superfici “virtuali” con ancoraggio forte poste
a distanza L = d + 2 L est. Il campo critico sarà, perciò, dato dall’espressione (35) con L al
posto di d. Si verifica facilmente che, se Lest << d, si ottiene proprio la (38).
L’introduzione del concetto di lunghezza di estrapolazione permette di capire quando
si può assumere che l’ancoraggio sia forte. Si potrà sempre assumere che l’ancoraggio sia
forte ogni volta che la lunghezza di estrapolazione è molto minore della lungezza
caratteristica della distorsione spaziale del direttore (ξH in questo caso ). In particolare, nel
12
caso in cui siano applicati campi magnetici od elettrici, l’ancoraggio può essere considerato
forte se la lunghezza di coerenza magnetica o quella elettrica sono molto maggiori della
lunghezza di estrapolazione.
VII- La transizione di saturazione.
Nei paragrafi precedenti abbiamo visto che una lamina di cristallo liquido sottoposta ad un
campo magnetico od elettrico orientato perpendicolarmente al direttore resta imperturbata per
campi magnetici ( o elettrici) inferiori ad un valore di soglia Hc (o Ec). Al disopra della soglia
il direttore tende a riorientarsi nella direzione del campo. Nella regione centrale della cella e
per campi sufficientemente elevati ( ξH << d), il direttore è praticamente parallelo al campo.
Sulle superfici il direttore tende anch’esso ad orientarsi lungo il campo ma è contrastato dalle
coppie di ancoraggio che tendono a mantenerlo orientato lungo l’asse facile. Se il campo è
sufficientemente elevato, cioè se ξH diventa confrontabile con la lunghezza di estrapolazione,
allora il direttore sulla superficie si discosta notevolmente dall’asse facile. Si dimostra
facilmente che, se il campo applicato è tale da soddisfare la condizione ξH ≥ Lest , allora il
direttore in superficie e in ogni altro punto del campione si orienta completamente nella
direzione del campo. In queste condizioni, il campione risulta dovunque orientato lungo il
campo. La rapida transizione dal regime distorto a quello uniforme viene detta transizione di
saturazione. All’aumentare del campo, immediatamente al disotto del punto di transizione,
l’angolo superficiale del direttore varia rapidamente al variare del campo fino a raggiungere
il valore ϕ1=π/2 in corrispondenza della soglia di saturazione Hs.
In condizioni usuali, la soglia di saturazione si raggiunge per campi molto superiori al
valore di soglia di Freederickz e, cioè quando le distorsioni orientazionali sono descritte in
modo molto accurato dall’approssimazione di campione semiinfinito (eq.(30)). Nel seguito
riportiamo i calcoli validi per la geometria di twist. In queste condizioni, l’eq.(27) deve valere
dovunque ed anche sulla superficie z = 0. Dunque:
dϕ o
cosϕ1
=+
(40)
dz z= 0
ξH
dove ϕ1 è l’angolo del direttore sulla superficie z = 0. D’altra parte, la condizione di equilibrio
dei momenti di forza elastici e di ancoraggio in supeficie è data dalla(20) che, nel caso di
un’energia di ancoraggio di Rapini-Papoular (eq.(21)), diventa:
dϕ
K2 o
= W 0 sin ϕ1 cosϕ1
(41)
dz z= 0
Sostituendo la (40) nella (41), si trova:
cosϕ1
K2
= W 0 sin ϕ1 cosϕ1
(42)
ξH
L’eq.(42) risulta sempre verificata se cos ϕ1=0 , cioè se ϕ1=π/2. Questa soluzione corrisponde
ad un’orientazione del direttore lungo il campo in ogni punto del cristallo liquido. Un’altra
possibile soluzione ( ϕ1≠π/2) si ottiene dividendo entrambi i membri della (42) per cos ϕ1≠0.
In tal caso si trova:
L
sin ϕ1 = est
(43)
ξH
la cui soluzione è:
L 
(44)
ϕ1 = arcsin est 
 ξH 
Poichè la funzione seno non può superare il valore 1, la soluzione (44) è valida solamente se
la lunghezza di coerenza magnetica è inferiore alla lunghezza di estrapolazione, cioè
solamente se il campo magnetico è inferiore ad un valore di soglia Hs dato da:
13
K2
1
(45)
∆χ m µ0 Lest
Si può dimostrare che, al di sotto di tale soglia, la soluzione in eq.(44) rappresenta un minimo
dell’energia mentre la soluzione ϕ1=π/2 rappresenta un massimo. Dunque, per campi
inferiori alla soglia di saturazione, l’angolo del direttore in superficie è quello dato dalla (44)
e, nel volume, il direttore ruota gradualmente fino a portarsi parallelo al campo lontano dalle
pareti. Per H che si avvicina ad Hs, l’angolo ϕ1 cresce fino a raggiungere il valore ϕ1=π/2
al punto di soglia (vedi figura 10). Al di sopra di tale campo, l’unica soluzione possibile
dell’equazione (42) resta solamente la soluzione ϕ 1=π/2 che corrisponde, adesso, ad un
minimo dell’energia. In figura 10 è riportato l’andamento dell’angolo superficiale in
funzione del campo applicato per campi molto superiori alla soglia di Freederickz.
Hs =
Figura 10. Angolo ϕ1 sulla superficie in funzione del rapporto H/Hs fra il campo e il campo di saturazione.
Simili risultati si ottengono se, invece della geometria di Twist, si considerano le altre
geometrie di fig.7a e 7b. I corrispondenti campi critici di saturazione sono:
K3
1
(46)
H sa =
∆χ m µ0 Lest
K1
1
(47)
∆χ m µ0 Lest
Si noti che le costanti elastiche sono scambiate rispetto ai corrispondenti campi critici di
Freederickz riportati nelle equazioni (36). Infatti, vicino alla transizione di Freederickz, il
direttore resta quasi dovunque parallelo all’asse facile ( θ ≈ 0 per la geometria di fig.7a e θ ≈
π/2 per la geometria di fig.7b) mentre vicino alla transizione di saturazione, il direttore è
quasi dovunque ortogonale all’asse facile ( θ ≈ π/2 per la geometria di fig.7a e θ ≈ 0 per la
geometria di fig.7b). Ne consegue che, ad esempio, nel caso di figura 7a, la costante elastica
efficace K(θ ) in eq.(6) si riduce a K1 per la transizione di Freederickz e a K3 per quella di
saturazione. Come per la transizione di Freederickz, anche adesso si deve rimarcare che la
soglia esiste solamente se il campo è perpendicolare all’asse facile.
Anche per la transizione di saturazione, risultati del tutto analoghi possono essere
ottenuti utilizzando un campo elettrico invece di un campo magnetico. In tal caso i campi
magnetici critici in equazioni (45)-(47) vanno sostituiti con i corrispondenti campi elettrici
critici che si ottengono sostituendo ∆ε e ε0 al posto di ∆χm e µ0 nelle equazioni. Si noti che, al
contrario di quanto avveniva nel caso della transizione di Freederickz, La soglia di
saturazione non è una soglia di tensione ma è una soglia di campo. Cioè, per un dato cristallo
liquido a condizioni fissate di temperatura e pressione, la soglia viene raggiunta per un ben
preciso valore del campo elettrico indipendentemente dallo spessore del campione. Dunque la
H sb =
14
tensione di soglia (V = E d) si abbassa al diminuire dello spessore d della lamina di
nematico.
In figura 11 sono riassunte schematicamente le transizioni che si realizzano in un
cristallo liquido nematico al variare del campo magnetico in geometria planare.
H
H<H c
Fig.11. Transizioni al variare del campo.
Hc < H < H*c
H > H*c