ISTITUTO TECNICO INDUSTRIALE STATALE
Albert Einstein
Vimercate (MI)
INFORMATICA E SISTEMI AUTOMATICI
ALGORITMI E DIAGRAMMI DI FLUSSO
Classi Terze
Indirizzo Liceo Scientifico Tecnologico
1
ALGORITMO: DEFINIZIONE
Dall’arabo al-Kuwārizmi a sua volta dal greco aritmhós,
un algoritmo è un metodo generale che risolve con una sequenza finita di
passi un problema dato
ALGORITMO: CONCETTO
• Algoritmo per un problema P:
descrizione, in termini di azioni elementari, di un procedimento che risolve P
• Approccio procedurale alla soluzione di problemi (esistono altri approcci: logici,
simbolici, funzionali, ...)
NON TUTTI I PROBLEMI SONO COMPUTAZIONALI
cioè non per tutti i problemi è possibile definire una procedura computazionale (un algoritmo)
che consenta, a partire dai dati di ingresso, di ottenere i risultati. Pertanto:
LA SCIENZA DEGLI ALGORITMI DEVE LIMITARSI A CONSIDERARE
PROBLEMI COMPUTAZIONALI
FORMULAZIONE DI UN PROBLEMA
Definizione dei dati e dei risultati che si vogliono ottenere (a partire dai dati).
Processo di formulazione di un problema:
• individuazione dei dati in ingresso (Es.: Problema P = scrivere i primi 10 numeri primi)
• individuazione dei risultati desiderati
PROBLEMI E ISTANZE DI UN PROBLEMA
• Specificando quali sono i dati di ingresso si definisce una istanza di problema
Ad esempio:
problema P: dato un naturale n calcolare la somma dei primi n Naturali
istanza di P: risolvere P per n = 12 (ovvero calcolare la somma dei primi 12 naturali)
• Un problema può essere visto come l’insieme di tutte le sue possibili istanze
TIPOLOGIE DI PROBLEMI
Esempio: il problema del commesso viaggiatore
“Un commesso viaggiatore deve percorrere il miglior tragitto attraverso le n città nelle quali deve
effettuare le consegne…”
Nota la mappa con l’indicazione delle n città da raggiungere, è possibile definire problemi di
diversa tipologia:
• Problemi di DECISIONE Æ Risultato: SI/NO
(es.: esiste un possibile percorso con una certa lunghezza?)
• Problemi di RICERCA Æ Risultato: una possibile soluzione
(es.: trovare un percorso di lunghezza minore di k)
• Problemi di ENUMERAZIONE Æ Risultato: conteggio delle soluzioni
(es.: quanti sono i percorsi di lunghezza minore di k)
• Problemi di OTTIMIZZAZIONE Æ Risultato: una soluzione ottima rispetto ad un obiettivo
(es.: trovare un percorso di lunghezza minima)
ELEMENTI DI UN ALGORITMO
• Passi elementari: azioni atomiche non scomponibili in azioni semplici
2
•
Processo: sequenza ordinata di passi
PROPRIETÀ DI UN ALGORITMO
Un algoritmo deve avere le seguenti proprietà:
• Finitezza: numero finito di passi elementari e di dati manipolati
• Determinismo: risultati non dipendenti dalla esecuzione
• Realizzabilità: compatibile con le risorse a disposizione
• Efficienza: minimo numero di operazioni da compiere
INDIVIDUAZIONE DI UN ALGORITMO
• attenta analisi del problema da risolvere
• definizione dei possibili ingressi e uscite
• definizione delle strutture dati
• suddivisione in sottoproblemi
• definizione della sequenza di passi risolutiva
ALGORITMI: CARATTERISTICHE
1. Le ISTRUZIONI (l’insieme ordinato di operazioni da eseguire) sono in numero finito;
2. Ogni istruzione è univoca cioè non lascia dubbi o ambiguità sul da farsi;
3. Esiste un esecutore (ad esempio, l’utilizzatore del PC) in grado di eseguire le istruzioni
4. Le procedure risolvono una CLASSE di problemi
5. Non esiste un modo UNICO per risolvere un problema
Un algoritmo è CORRETTO se per ogni istanza di input termina con l’output corretto
RAPPRESENTAZIONE DI UN ALGORITMO: FLOW-CHART
Per rappresentare un algoritmo occorre individuare:
• i passi necessari per raggiungere la soluzione
• la loro corretta sequenza logica
Lo strumento più utilizzato per la rappresentazione di un algoritmo è il diagramma di flusso o
flow-chart. Esso è un formalismo grafico che rappresenta una descrizione più efficace e
meno ambigua di una descrizione a parole.
Gli elementi fondamentali di un flow-chart rappresentano una schematizzazione grafica della
sequenza logica (flusso di esecuzione) dei passi di un algoritmo:
• trasferimento di informazioni (dati e risultati)
• esecuzione di calcoli
• assunzione di decisioni
• esecuzioni di iterazioni
Gli elementi base di un flow-chart sono due:
• nodi (simboli grafici di forma diversa)
• archi
che assumono significato e forme diverse a seconda della funzione rappresentata:
3
SIMBOLO
DESCRIZIONE
Identifica l’inizio (START) e la fine (STOP) della sequenza
logica di passi di un algoritmo.
Viene utilizzato per indicare una elaborazione (ad
esempio, formula matematica) o assegnamento di un
valore ad una variabile (ad esempio, x=2).
Identifica le operazioni di INPUT dei dati.
Identifica le operazioni di OUTPUT dei risultati
Si inserisce nella sequenza logica dei passi di un
algoritmo ogni qualvolta vi è la necessita di prendere una
decisione di tipo booleano (vero/falso, si/no, 0/1, …).
Questo simbolo non identifica un passo dell’algoritmo ma
viene di solito utilizzato per chiudere le strutture
informatiche fondamentali.
Le frecce danno informazione sul verso del flusso
esecutivo di processo.
ESEMPIO DI ALGORITMO RAPPRESENTATO MEDIANTE FLOW-CHART
Inizia la
sequenza logica
dei passi
Legge il valore
assunto dalla
variabile
denominata Var1
Indica che la
sequenza di passi
continua alla
sezione 1
START
1
Var1
Somma Å Var1+Var2+Var3
Calcola il valore
della somma dei
valori assunti
dalle tre variabili
Var2
Somma
Stampa il valore
della variabile
Somma
Var3
STOP
1
Il simbolo Å presente nel blocco “Somma ...” indica
l’assegnazione del valore assunto dall’espressione a
secondo membro alla variabile dichiarata a primo
membro. Rappresenta, in informatica, un simbolo più
adatto per indicare l’uguaglianza.
4
IL LINGUAGGIO DEI DIAGRAMMI DI FLUSSO
• sono linguaggi grafici e perciò adatti alla descrizione di processi sequenziali; un processo
è sequenziale quando la esecuzione di una qualsiasi azione non può mai sovrapporsi
alla esecuzione di un’altra azione.
• la descrizione della soluzione ad un problema è inequivocabile, infatti i legami tra le
azioni e i controlli è rappresentato tramite segni grafici a cui sono associati specifici
significati;
• è un linguaggio adatto, essendo grafico, per comunicare un ALGORITMO ad un
esecutore umano e non da una macchina.
Il diagramma di flusso è un grafo contenente:
• un blocco iniziale
• un blocco finale
• un numero finito di blocchi di azione
• un numero finito di blocchi di controllo
per il quale valgono le seguenti condizioni:
1. Ciascun blocco di AZIONE ha una freccia entrante ed una uscente (fig. 1);
2. Ciascun blocco di CONTROLLO ha una freccia entrante e due uscenti (fig. 2);
3. Ciascuna FRECCIA entra in un blocco oppure in un nodo di chiusura (fig. 3);
4. Ciascun blocco è raggiungibile dal blocco INIZIALE;
5. Il blocco FINALE è raggiungibile dal blocco iniziale
Fig.1
Fig.2
Fig.3
LE STRUTTURE INFORMATICHE FONDAMENTALI
Fra i possibili modi di connettere blocchi elementari e frecce che rispettino la definizione di grafo
di flusso, ci sono i cosiddetti schemi di composizione o strutture informatiche fondamentali,
chiamati Sequenza, Selezione e Iterazione.
• Schema di SEQUENZA
Descrive la composizione sequenziale di due o più azioni elementari di un processo.
START
A1
A2
STOP
5
•
Schema di SELEZIONE
In dipendenza dall’esito di un controllo o test il comportamento è differente: si dovrà
eseguire l’azione A1 se C è vero, mentre l’azione da eseguire sarà A2 se C è falso.
Questo tipo di struttura può essere ulteriormente semplificata, eliminando A1 oppure A2
dallo schema.
V
A1
•
C
F
A2
Schema di ITERAZIONE
Esistono due modelli di iterazione (o cicli) ed entrambi servono per descrivere che
l’azione deve essere ripetuta quando l’esito del controllo lo richiede. Ogni schema
fondamentale ha un unico punto di ingresso ed un unico punto di uscita. Si parla di
iterazione con controllo in testa quando la condizione di iterazione è eseguita prima
delle eventuali azioni, mentre si dice che una iterazione è con controllo in coda se la
condizione di iterazione è eseguita successivamente alla prima esecuzione delle azioni.
A
V
C
F
ITERAZIONE CON
CONTROLLO IN TESTA
A
V
C
F
ITERAZIONE CON
CONTROLLO IN CODA
6
La differenza sostanziale fra i due modelli di iterazioni è che se il controllo C, in testa,
risulta inizialmente falso l’azione A non verrà mai eseguita, a differenza dell’iterazione
con controllo C in coda dove l’azione A viene eseguita almeno una volta.
Di solito le strutture iterative prevedono l’utilizzo di un contatore di ciclo che può
rappresentare anche la variabile di controllo C; in tal caso il contatore va sempre
inizializzato al di fuori del ciclo (prima di inserire la strutture iterativa) e incrementato o
decrementato al suo interno:
Inizializzazione
CONT Å 0
Incremento
CONT Å CONT +1
A
CONT <= 10
V
C
F
FLOW-CHART STRUTTURATI
Sono strutturati quei grafi di flusso che possono essere ricondotti ai tre schemi di composizione
fondamentali.
• Un flow-chart composto da una azione racchiusa tra inizio e fine è un flow-chart
strutturato (fig. 1).
• Se si hanno due flow-chart strutturati S1 ed S2 , la loro composizione secondo lo
schema di sequenza produce un flow-chart strutturato (fig. 2a, 2b, 2c).
• Se si hanno due flow-chart strutturati S1 e S2 ed un blocco di controllo C, sono strutturati
i flow-chart che si ottengono componendo essi secondo lo schema di selezione (fig. 3a,
3b, 3c).
• Se si hanno uno schema strutturato S e un blocco di controllo C (fig. 4a, 4b), allora sono
strutturati anche i flow-chart che si ottengono componendoli secondo gli schemi di
iterazione. (fig. 4c, 4d).
• Nessun altro tipo di flow-chart è strutturato.
7
START
START
START
START
A
S1
S2
S1
STOP
STOP
STOP
S2
Fig. 1
Fig. 2a
Fig. 2b
STOP
Fig. 2c
V
S1
Fig. 3a
C
F
V
S2
C
F
V
S1
Fig. 3b
C
F
S2
Fig. 3c
8
S
S
V
C
S
S
F
C
F
C
F
V
Fig. 4a
Fig. 4b
V
C
V
F
Fig. 4c
Fig. 4c
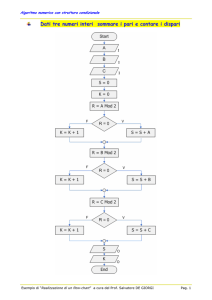
ESEMPIO
START
V
C
F
A1
C1
A2
F
V
V
F
S1
Iterazione con
controllo in coda
S
Selezione
C2
STOP
S2
Iterazione con
controllo in testa
9
TEOREMA DI JACOPINI-BÖHM
Dato un processo ‘P’ ed un grafo che lo descrive, è sempre possibile determinare un
processo ‘Q’ che sia descrivibile tramite un diagramma di flusso strutturato.
Due processi, che agiscono sullo stesso insieme di oggetti, si dicono EQUIVALENTI se
producono lo stesso effetto.
Due programmi equivalenti sottoposti agli stessi dati di ingresso o non terminano oppure
terminano entrambi producendo gli stessi dati di uscita.
RIFLESSIONI SUI DIAGRAMMI DI FLUSSO
• I diagrammi di flusso sono adatti alla comunicazione inter-umana, in quanto risultano per
noi di facile comprensione;
• Uno stesso diagramma di flusso è convertibile in più programmi codificati con diversi
linguaggi di programmazione.
• I diagrammi di flusso sono ingombranti, quasi mai entrano su un singolo foglio: ciò rende
difficile sia seguire il flusso di controllo che eseguire modifiche al diagramma.
• La notazione dei diagrammi di flusso non è naturalmente strutturata.
• Le modifiche tendono a de-strutturare il grafo.
AZIONI COME ISTRUZIONI
Ci sono tre tipologie di istruzioni:
• Assegnamento ed istruzioni aritmetico-logiche
Ö A = 5 (assegnamento di valori a variabili)
Ö A = A + 1 (assegnamento con istruzione aritmetica)
• Condizioni booleane
Ö A=5
(true se il valore di A è uguale a 5, false altrimenti)
Ö A>5
(true se il valore di A è maggiore di 5, false altrimenti)
Ö A<5
(true se il valore di A è minore di 5, false altrimenti)
Ö A >= 5 (true se il valore di A è maggiore o uguale a 5, false altrimenti)
Ö A <= 5 (true se il valore di A è minore o uguale a 5, false altrimenti)
Ö A <> 5 (true se il valore di A è diverso da 5, false altrimenti)
• Istruzioni di I/O
Ö Permettono di leggere valori di input ed assegnarli a variabili di processo
leggi A (vuol dire che ad A viene assegnato il valore letto)
Ö Permettono di scrivere i valori memorizzati dalle variabili di processo
scrivi A (vuol dire che viene stampato il valore di A)
STRUTTURA INFORMATICA “CASE”
Oltre ai tre schemi di composizione fondamentali, sequenza, selezione e iterazione, è
importante considerare anche la struttura cosiddetta case che rappresenta un insieme di
selezioni annidate. Infatti, nelle situazioni in cui è indispensabile realizzare più selezioni fra loro
annidate si può sostituire l’insieme di schemi semplici con un’unica struttura che, in modo più
lineare, comprende tutti i possibili “casi” che possono verificarsi. Ovviamente, la condizione di
10
selezione non è in questo caso di tipo booleano (due possibili valori assunti) ma diventa
l’assegnazione di un valore, ad una variabile S, detta variabile di switch.
1
A1
S
2
3
A2
N
A3
AN
In tal caso, a seconda del valore assunto dalla variabile S (1,2, … ,N) la struttura esegue uno
“switch” ad uno dei “case” previsti (Case 1,Case 2, … ,Case N), eseguendo le azioni ad esso
relative (A1,A2, … ,AN). La struttura si presenta quindi come strumento indispensabile per la
costruzione di algoritmi viste le potenzialità e la semplicità di utilizzo.
11