Meccanica = studio del moto dei corpi
Cinematica: studio del moto indipendentemente dalle cause
Dinamica: studio del moto in relazione alle forze agenti
Statica: studio delle condizioni di equilibrio
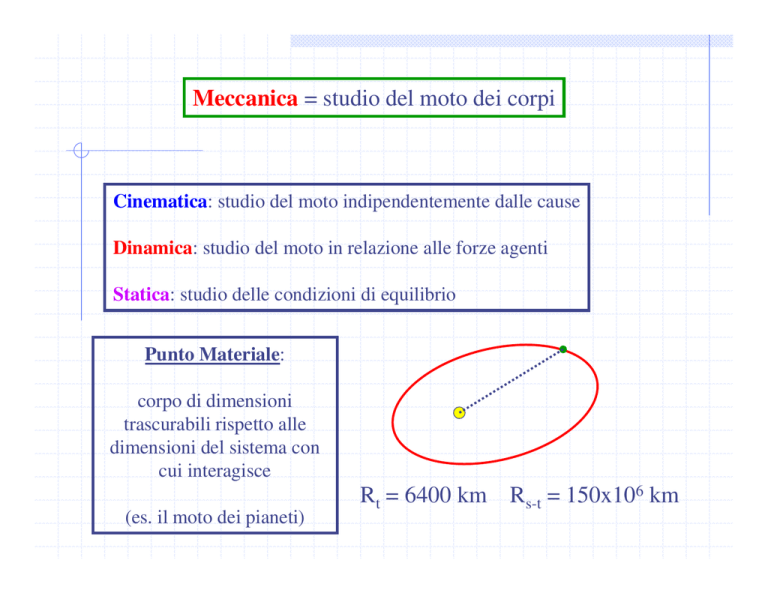
Punto Materiale:
corpo di dimensioni
trascurabili rispetto alle
dimensioni del sistema con
cui interagisce
(es. il moto dei pianeti)
Rt = 6400 km Rs-t = 150x106 km
Traiettoria di un punto materiale: insieme dei punti dello spazio
raggiunti da P al trascorrere del tempo.
z
s
O
r
x
vettore posizione: r = r(t)
s = s(t) legge oraria
P
y
P≡(x,y,z) x = x(t), y = y(t), z = z(t)
z
P1
∆r = r(t2)-r(t1) = P1P2
∆r
P2
r(t1)
O
x
r
vm =
t
velocità media
r(t2)
y
r dr
v = lim
=
dt
t →0 t
[v]=[LT-1]
S.I.
m/s
C.G.S. cm/s
velocità istantanea
s
B
s2
s1
s BC
vm =
=
= tgα
t AC
A
t1
s
t2
t
s1
r dr
v = lim
=
= tgα '
dt
t →0 t
B
s2
A
t1
’
t2
significato geometrico della velocità istantanea:
tangente trigonometrica dell’angolo α’ formato dalla retta
tangente alla traiettoria con l’asse delle ascisse
t
v1
z
P2
P1
v1
v2
∆v
r(t1)
v2
r(t2)
O
∆v = v2-v1
y
x
v
am =
t
[a]=[LT-2]
a = lim
t →0
v dv d 2 r
=
= 2
t dt dt
accelerazione media
S.I.
m/s2
C.G.S. cm/s2
accelerazione istantanea
In un moto curvilineo l’accelerazione istantanea è diretta verso
il centro della traiettoria s.
P1
v1
P2
P
v1
v2
∆v
v2
an
at
a
Possiamo scomporre a in 2 componenti, tangente e normale a s
at rappresenta la misura della variazione del modulo della velocità nell’unità di tempo
an rappresenta la misura della variazione della direzione della velocità nell’unità di tempo
at = 0 moto uniforme (|v| = costante)
an = 0 moto rettilineo (direzione di v
costante)
Moto uniforme
moto uniforme
inoltre se an = 0
st − s0
v=
t
st = s0 + vt equazione oraria
|v| = costante, at = 0
moto rettilineo uniforme.
s
v>0 moto progressivo
α
v = tg α
t
v<0 moto regressivo
moto uniformemente vario:
at = costante ≠ 0
a>0 moto uniformemente accelerato
v
se v0 = 0 moto
naturalmete vario
vt − v 0
a=
t
vt = v0 + at
t
a<0 moto uniformemente ritardato
v
1 2
at
2
1
vt − v0 = at → AT = t (vt − v0 )
2
v0t
1 2
st − s0 = v0t + at
2
v0
o
t
equazione
oraria
1 2
st = s0 + v0t + at
2
vt = v0 + at
vt2 = v02 + 2ast
v
ds
v=
dt
v0
s
o
s=
t
t2
t1
ds = vdt
v(t )dt
Moto verticale dei gravi
o
h
P
t
suolo
1 2
s = s0 + v0t + gt
2
v = v0 + gt
v 2 = v02 + 2 gs
Tutti i corpi cadono nel vuoto con
accelerazione costante
(esperienza di Galileo). |g| = 9.8 m/s2
Esempio: lancio di un grave verso l’alto.
Problema: determinare hmax, t(hmax) e t di volo (ttot)
y
hmax
1 2
s = s0 + v0t − gt
2
v = v0 − gt
v 2 = v02 − 2 gs
suolo
v(hmax ) = 0
v0
t (hmax ) =
g
v02
s = hmax =
2g
1
s − s0 = v0t − gt 2 = 0
2
t1 = 0
t2 =
2v0
g
Moto di un
proiettile
Moto composto da 2 moti indipendenti:
rettilineo uniforme lungo l’asse x
e
uniformemente accelerato lungo l’asse y












