x
z
y
Fisica II - CdL Chimica
Corrente di spostamento
Applichiamo il teorema di Ampere nel caso di un
condensatore, considerando le sup. S1 ed S2:
B d s m I
L’integrale di linea è esteso a
qualsiasi percorso chiuso concatenato con la
0
corrente di conduzione.
• Le due superfici S1 e S2 sono delimitate dallo
stesso percorso P.
• Non essendo presente una corrente di
conduzione tra le due armature, si hanno
due risultati diversi (m0I e 0) !!!
• Il teorema di Ampere in questa forma è valido
solo se la corrente di conduzione è continua nello
spazio.
• Per risolvere l’incongruenza Maxwell introdusse
la
Corrente di spostamento
dE
IS 0
con E E d A flusso campo
elettrico
dt
Fisica II - CdL Chimica
Teorema di Ampere generalizzato
I S 0 d E dt
Bd s m0 I I S m0 I m0 0
dE
Teorema di Ampere-Maxwell
dt
I campi magnetici sono generati sia dalle correnti di
conduzione sia dai campi elettrici variabili !
Fisica II - CdL Chimica
Le equazioni di Maxwell
I:
II :
E d A
Q
0
Bd A 0
dB
III : E d s
dt
IV :
Bd s m0 I m0 0
Teorema di Gauss (flusso elettrico totale
attraverso superficie chiusa = carica netta)
Flusso magnetico netto attraverso una
superficie chiusa è nullo (teorema Gauss
per il magnetismo)
Legge di Faraday dell’induzione
dE
dt
Teorema di Ampere generalizzato
Noti i campi elettrico e magnetico, in un punto, la forza agente su una
carica elettrica è data da
F qE qv B
Questa relazione insieme alle 4 equazioni di Maxwell, fornisce una
descrizione completa di tutte le interazioni elettromagnetiche
classiche.
Fisica II - CdL Chimica
Eq. fondamentali dell’elettromagnetismo
Fisica II - CdL Chimica
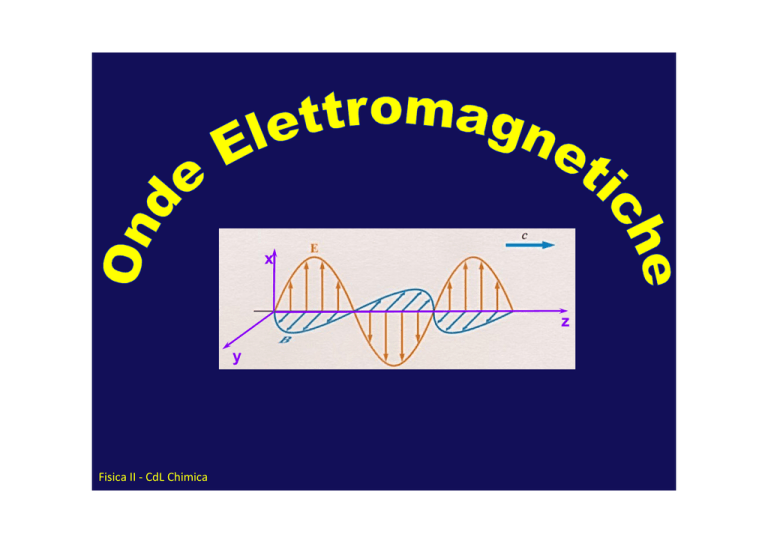
Onde Elettromagnetiche
Maxwell dimostrò che i campi elettrici
e magnetici dipendenti dal tempo
soddisfano una equazione d’onda.
La più importante conseguenza di
questa teoria è la previsione
dell’esistenza delle onde
elettromagnetiche (campi elettrici e
magnetici oscillanti).
Non vi è necessità di un mezzo di
supporto (propagazione nel vuoto).
La variazione dei campi crea
reciprocamente il mantenimento della
propagazione dell’onda: un campo
elettrico variabile induce un campo
magnetico e viceversa.
I vettori E e B sono tra di loro e
alla direzione di propagazione.
Fisica II - CdL Chimica
Calcolo equazione d’onda
Assumiamo che un’onda e.m. piana si
propaghi in direzione x , con E in
direzione +y e B in direzione +z.
Consideriamo il percorso rettangolare in figura :
E
in una direzione E x dx, t E x, t
dx
x
dalla III eq. Maxwell circuitazione lati superiori 0
E
E
s
,
,
d
E
x
dx
t
E
x
t
dx
x
flusso B concatenato con il rettangolo B Bdx
dB
dB
B
derivando rispetto a t
dx
dx
dt
dt x cost
t
sostituendo nella III eq. di Maxwell
dB
E
s
d
dt
B
E
B
E
dx
dx
t
x
t
x
Fisica II - CdL Chimica
Calcolo equazione d’onda
dE
dt
B
B
d
s
B
x
,
t
B
x
dx
,
t
dx
x
Il flusso elettrico concatenato vale E E dx
dE
E
derivando rispetto al tempo
dx
dt
t
sostituendo insieme al precedente nella IV eq. Max.
B
E
B
E
dx
dx
m
m
0 0
0 0
x
t
x
t
derivando rispetto ad x la e sostituendo
2 E
B
B
E
m
0 0
x 2
x t
t x
t
t
2 E
2 E
0 m0 2
x 2
t
Dalla IV eq. Maxwell
Bds m0 I m0 0
analogamente, derivando rispetto a t la e sostituendo
2 B
E
E
2 B
2 B
1 B
0 m0 2
t 2
t x
x t
x 0 m0 x
x 2
t
Fisica II - CdL Chimica
Calcolo equazione d’onda
2 E
2 E
2 B
2 B
1
e
sono
eq
onda
lineare
di
velocità
c
m
m
.
0 0
0 0
x 2
t 2
x 2
t 2
0m
con soluzioni :
E Emax cos k x w t
2 2 f
con k
e w 2 f
B Bmax cos k x w t
c
l
0 8.85418 10
12
C2
N m2
Tm
si trova che
A
1
m
c
2.99792 108
s
0 m0
m0 4 107
velocità luce nel vuoto
La luce è un’onda elettromagnetica !!!
Fisica II - CdL Chimica
Calcolo equazione d’onda
E Emax cos k x w t rispetto ad x
Calcolando le derivate parziali di
B Bmax cos k x w t rispetto ad t
E
kEmax sin k x w t
E
B
x
dovendo essere
kEmax w Bmax
B
x
t
w Bmax sin k x w t
t
E
E
2 2
essendo w 2 e k
si ha max c
c !!!
l
c
Bmax
B
In ogni istante, in un’onda elettromagnetica, il
rapporto tra il modulo del campo elettrico ed il
modulo del campo magnetico è uguale alla velocità
della luce !!!
Fisica II - CdL Chimica
VC
UE
0
C
L
1
t
VL
Circuiti
LC
0
1
t
Fisica II - CdL Chimica
UB
t
Onde Hertziane
Si può mettere in evidenza l’esistenza delle onde
elettromagnetiche previste dalla teoria di Maxwell ?
Sì, nel 1887 Hertz mise a punto un sistema
per la generazione e rivelazione delle onde
elettromagnetiche (onde radio).
Fisica II - CdL Chimica
Oscillazioni Elettromagnetiche
Analogia con la meccanica:
Rammentiamo l’oscillatore meccanico massa-molla
k = costante elastica
d 2x
m 2 kx
dt
sol.: x A cos w t
-A
+A
A = ampiezza delle oscillazioni
Fisica II - CdL Chimica
Circuito LC
Consideriamo un semplice circuito LC.
Il condensatore ha una carica iniziale
Qmax e l’interruttore viene chiuso al
tempo t=0.
I(t)
Q Idt
V
C
C
C
la caduta di tensione è
determinata dall’integrale
della corrente sulla
capacità
I(t)
2
L
Fisica II - CdL Chimica
dI
d Q
V L
L 2
dt
dt
la caduta di tensione è
determinata dalla
derivata della corrente
per l’induttanza
Circuito LC
Applichiamo la regola delle maglie al
circuito LC.
Q
dI
L 0
C
dt
dQ
Q
d dQ
essendo I
si ha
L
dt
C
dt dt
2
d Q
1
Q
2
dt
LC
2
analoga a
d x
k
x
2
dt
m
La carica nel circuito oscillerà in modo
analogo alla massa con la molla:
1
w
LC
1
f0
2 LC
2
Fisica II - CdL Chimica
Soluzione:
Q Qmax cos wt
dQ
I
wQmax sin wt
dt
Energia
immagazzinata
frequenza di risonanza
Q2
1
UE
U B LI 2
2C
2
Oscillazioni di Energia
T = periodo di oscillazione
Consideriamo un circuito LC:
C carico, al tempo t=0 si chiude S.
Il condensatore si scarica, la
corrente aumenta, l’energia si
trasferisce dal campo elettrico a
quello magnetico. Poi il ciclo si
inverte e proseguirebbe all’infinito
in assenza di meccanismi
dissipativi.
Fisica II - CdL Chimica
Generazione di onde elettromagnetiche
Quale configurazione di cariche e correnti elettriche produce
un’onda elettromagnetica ?
Carica in moto a velocità costante: campo elettrico + campo
magnetico stazionari, nello spazio esiste una densità di energia,
costante nel tempo, associata ai suddetti campi.
In questo caso non vi è trasporto di energia né di quantità di moto
e non sussiste radiazione elettromagnetica.
Per produrre un’onda elettromagnetica è necessario accelerare la
carica.
Il moto accelerato della carica corrisponde a una corrente che
varia nel tempo: la radiazione è prodotta da correnti che variano
nel tempo.
Le onde elettromagnetiche trasportano energia e quantità di moto
nello spazio attraverso i loro campi elettrici e magnetici oscillanti.
Cariche a riposo e cariche in moto a velocità costante non
irraggiano, mentre le cariche accelerate irraggiano.
Fisica II - CdL Chimica
Esperimento di Hertz
trasferimento di energia elettromagnetica
Dispositivo di Hertz per generare e
rivelare onde elettromagnetiche: due
elettrodi sferici connessi ad una bobina
d’induzione che fornisce brevi impulsi di
tensione alle due sfere e innesca una
scarica oscillante. Il ricevitore è un
circuito vicino contenente un secondo
spinterometro.
Hertz trovò che l’energia viene spedita
dal trasmettitore al ricevitore quando la
frequenza di risonanza del ricevitore
veniva accordata con quella del
trasmettitore. L’energia è trasportata da
onde elettromagnetiche.
Es.: radio FM, TV, telefonia radiomobile
Fisica II - CdL Chimica
Generazione di onde elettromagnetiche
Un circuito oscillante RLC, con un generatore esterno che rifornisce
l'energia dissipata nel circuito o portata via dalla radiazione. La corrente
nel circuito varia sinusoidalmente con la pulsazione risonante w.
Il circuito oscillante è accoppiato
attraverso un trasformatore a
una linea di trasmissione, che
serve a portare la corrente a una
antenna. (I cavi coassiali, che
portano i segnali TV in molte case,
sono esempi comuni di linee di
trasmissione.)
L'antenna è un dipolo elettrico oscillante: sui due rami si trovano cariche
istantanee opposte che variano sinusoidalmente nel tempo. Le cariche sono
inevitabilmente accelerate muovendosi avanti e indietro nell'antenna, e
come risultato l'antenna è una sorgente di radiazione di dipolo elettrico.
Fisica II - CdL Chimica
Energia trasportata dalle onde e.m
Flusso di energia in un’onda elettromagnetica = vettore di Poynting S
S
1
m0
poichè E B EB si ha S
E B
EB
m0
E 2 cB 2
B E c da cui S
valore istantaneo di S
m0 c m0
Il modulo di S è legato alla rapidità con cui l’energia è trasportata
dall’onda attraverso un’area unitaria, nell’unità di tempo:
S
Energia
tempo
Potenza
area
area
unità di misura : Watt m 2
La direzione del vettore di Poynting S coincide in ogni punto con la
direzione di propagazione dell’onda e con la direzione in cui è
trasportata l’energia.
Fisica II - CdL Chimica
Energia trasportata dalle onde e.m
Dalle soluzioni ricavate dalle eq. di Maxwell per i campi elettrico e
magnetico di un’onda elettromagnetica :
E Emax cos k x w t
B Bmax cos k x w t
Se l ' onda è sinusoidale occorre fare il valore medio temporale di cos 2 kx wt
2
2
EB med Emax Bmax Emax
cBmax
1
2
essendo cos kx wt
si ha I Smed
m0
2
2 m0
2 m 0c 2 m0
2
1
B2 E c
1
2
In termini di densità di energia uE 0 E u B
0E2
2
2 m0
2 m0
2
2
B
quindi uE u B , u uE uB 0 E 2
m0
mediando su un ciclo umed
2
1
1 Bmax
2
ed , infine, I Smed cumed
0 Emax
2
2 m0
L’intensità di un’onda elettromagnetica è uguale al prodotto della
densità di energia media per la velocità della luce.
Fisica II - CdL Chimica
Pressione di radiazione
Il campo elettrico di un'onda elettromagnetica incidente su una
superficie esercita una forza sugli elettroni imprimendo loro una
accelerazione. Negli urti con gli atomi del corpo, essi possono trasferire
l'energia di cui sono dotati e quindi incrementarne la temperatura.
Di fatto l'onda esercita una forza netta sul corpo investito nella stessa
direzione del suo moto. Si tratta normalmente di una forza piccolissima,
(5*10-6 Nm-2 per luce solare diretta) che tuttavia risulta misurabile in
laboratorio con metodi accurati.
Un'onda piana luminosa incidente, agisce su un
elettrone in un sottile foglio resistivo. Sono
indicati i valori istantanei di E, B, della velocità
di deriva dell'elettrone vd e della forza di
radiazione FB.
La pressione della radiazione che incide sullo specchio
provoca una torsione della fibra di un angolo piccolissimo.
Fisica II - CdL Chimica
Spettro delle onde elettromagnetiche
Le onde elettromagnetiche viaggiano nel
vuoto con velocità c, frequenza f e
lunghezza d’onda l. I vari tipi di onde
elettromagnetiche, prodotte tutte da
cariche accelerate, sono mostrate in
figura.
Es.: onda radio di frequenza f=94.7MHz
l = c/f = 3.17 m
Fisica II - CdL Chimica
Applicazione: forno a microonde
In un tipico forno a microonde le onde
elettromagnetiche stazionarie hanno lunghezza d’onda
l=12.2 cm (f=2.5 GHz), fortemente assorbita dalle
molecole d’acqua contenute nei cibi. Poiché i nodi
dell’onda (campo elettrico nullo) sono separati da
l/2=6.1 cm, le pietanze devono essere ruotate per
garantire un riscaldamento uniforme.
Fisica II - CdL Chimica












