Università di Bologna
Dipartimento di Filosofia e comunicazione
Corso di Filosofia del linguaggio LM 2014/15
l’ultima foto di
Ludwig
Wittgenstein
per i corsi di laurea in
Semiotica (6 o 12 cfu), Geografia e processi territoriali (6 cfu),
Italianistica, culture letterarie europee, scienze linguistiche - curriculum
italianistica (6 cfu), Italianistica, culture letterarie europee, scienze
linguistiche – curriculum italianistica e scienze linguistiche (6 cfu), Lingue
e letterature moderne, comparate e postcoloniali(6 cfu).
3ª settimana
20 ottobre 2014
21 ottobre 2014
22 ottobre 2014
27 ottobre 2014
28 ottobre 2014
29 ottobre 2014
3 novembre 2014
4 novembre 2014
5 novembre 2014
17 novembre 2014
Le Ricerche filosofiche I, 80-100
Le Ricerche filosofiche 101-133: regole e confini, la filosofia come attività e
non come dottrina
Discussione sulle Ricerche filosofiche I, 139-165: leggere e comprendere
Le Ricerche filosofiche I, 165-197: sul comprendere
Le Ricerche filosofiche I, 198-219: sulle regole
Discussione sulle Ricerche filosofiche I, 220-242:
Le Ricerche filosofiche I, 243-315 1ª: le sensazioni, l’espressione del dolore
Le Ricerche filosofiche I, 243-315 2ª: l’impossibilità di una lingua privata
Una prima conclusione
Nella settimana 10-16 novembre NON c’è lezione
Riprendono le lezioni per chi segue il corso per 12 crediti
Prima di riprendere la lettura e il commento delle Ricerche di Wittgenstein,
come la settimana scorsa, vorrei fare il punto su alcune cose viste la scorsa
settimana. Ne vorrei toccare quattro, una davvero brevissimamente: il
significato come uso, le regole (brevissimamente), il metro campione,
somiglianze di famiglia e concetti.
Significato come uso. Se leggete il Cratilo di Platone, vedrete che lì la
contrapposizione fra i due protagonisti, Ermogene e Cratilo, è fra
convenzionalità e naturalità della lingua, posizioni sulle quali Socrate riflette,
opponendo al primo il naturalismo e al secondo il convenzionalismo, a mio
avviso cercando una via intermedia che però non viene propriamente fuori
ed è rimandata a un seguito del dialogo che non è mai seguito. Ora
2
Wittgenstein nel Tractatus sembra proporre una soluzione naturalista
abbastanza inventiva. Platone nel Cratilo considera l’opinione che le parole
prime – cioè quelle il cui significato non deriva da quello di altre parole per
composizione di più parole, o, come avviene negli usi metaforici, per
sottrazione di alcuni tratti di una parola – considera, dicevo, che le parole
prime siano immagini sonore di ciò che nominano. Nel Tractatus, W
afferma che la proposizione elementare (l’enunciato elementare) sia
l’immagine di uno stato di cose, col quale condivide la struttura. Dunque i
nomi non sarebbero immagini, ma gli enunciati elementari sì. Nelle Ricerche,
invece, l’idea che il significato di una parola sia il modo del suo uso, sembra
una posizione convenzionalista. Gli uomini usano una parola per parlare di
una cosa, o per caratterizzarla, o per contare le cose, e quella parola sarà
quindi un nome proprio, per es, un nome comune o un numero.
Negli ultimi 60 anni sono state proposte moltissime specificazioni del
significato come uso, tutte più “tecniche” di quella di W. Il
comportamentismo linguistico di Willard van Orman Quine, le condizioni
di asseribilità di Michael Dummett, e poi in versione diversa di Dag Prawitz
– ispirate rispettivamente dalla logica intuizionista e dalla teoria della
dimostrazione, la semantica basata sulla teoria dei giochi di Jaakko Hintikka,
la semantica del ruolo concettuale – con le sue sottovarianti dovute a
Hartry Field, Bas van Fraassen e Gilbert Harman – e, negli anni ‘90,
l’inferenzialismo semantico di Robert Brandom e il minimalismo semantico
di Paul Horwich. (Per citare solo le varianti principali.) Tutte queste teorie
assumono che le parole abbiano un significato e che questo funzioni come
dice una teoria comportamentista, o come accade in una logica
costruttivista, o nella teoria dei giochi, ecc. Questo può forse essere
riespresso sostenendo che una lingua è un prodotto culturale, e
aggiungendo che ci è possibile imparare una lingua perché siamo
naturalmente dotati di quanto serve per impararla (e c’è molto da discutere
su cosa serva per imparare una lingua). La mia impressione è però che
nessuna di queste teorie entri nel dettaglio e spieghi come un uso si
stabilisca, come si mantenga e come muti (qualcuno accenna qualcosa,
come Horwich). (Non che non ci siano linguisti, come David Lightfoot,
che se ne siano occupati meglio.)
La questione centrale, dal mio punto di vista, però è quali elementi
cognitivi siano implicati in questi dettagli – percezione, attenzione, memoria,
ecc. Perché il primo uso in qualche modo è già significante.
Regole. W ha molte idee sulle regole, e l’idea fondamentale è che una regola
non può essere ridotta alla sua formulazione. Un tipo tutto speciale di
regole sono le norme. Le norme sono regole introdotte da un’autorità.
Qualunque giurista, giudice, avvocato sa bene che una norma non si riduce
3
alla sua formulazione, seppure la storia del diritto sia tutta tesa a formulare
nella maniera migliore ciascuna norma in modo da ridurre il contenzioso su
cosa una norma prescrive.
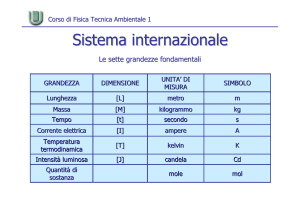
Il metro campione. §50 (rileggere tutta la sezione.) Scrive W: «Di una cosa
non si può affermare e nemmeno negare che sia lunga un metro: del metro
campione di Parigi.» Qui W sembra perseguire una netta distinzione fra
espressioni che riguardano la lingua e espressioni che riguardano il mondo.
La questione ha un precedente importante:
Moritz Schlick (1918-25), il fondatore del Circolo di Vienna, che
Wittgenstein tra il 1926 e il 1928 incontrerà più volte, avanza un’idea che è
ripresa nel 1928 da Reichenbach, parlando di definizioni coordinative,
definizioni che coordinano concetti e oggetti nella fisica, che servono
innanzitutto per introdurre unità di misura. (Non so affatto se W
conoscesse questa idea di Schlick.) Scrive Reichenbach:
Di principio, un’unità di lunghezza può essere definita sulla base di
un’osservazione che non comporti alcuna relazione metrica, come ‘la lunghezza
d’onda di una luce di una certa intensità di rosso’. In questo caso un campione
di questo colore rosso andrebbe conservato a Parigi al posto del metro
campione. La caratteristica di questo metodo è coordinare un concetto con un
oggetto fisico. (Reichenbach 1928: 15, trad. it. mia, cfr. trad. it. di Adriano
Carugo: 40-1.)
Una definizione coordinativa trasforma un campione in uno standard,
collegando il piano oggettuale con quello linguistico-concettuale. Non dà
informazioni, offre uno strumento per raccoglierne.
La questione ha anche un seguito, in Kripke:
A tal proposito Wittgenstein dice qualcosa di molto misterioso: “Di una cosa
non si può affermare e nemmeno negare che sia lunga un metro: dcl metro
campione di Parigi. Naturalmente con ciò non gli abbiamo attribuito nessuna
proprietà straordinaria, ma abbiamo soltanto caratterizzato la sua funzione
particolare nel gioco di misurare con il metro”. Sembra che questa sia
veramente una “proprietà straordinaria” per qualunque sbarra. Penso che
Wittgenstein abbia torto. Se la sbarra è una sbarra lunga, ad esempio, 39-37
pollici (nell’ipotesi di avere a disposizione qualche campione diverso per i
pollici), perché non dovrebbe essere lunga un metro? Ad ogni modo,
supponiamo che egli abbia torto e che la sbarra sia lunga un metro. Parte del
problema che tormenta Wittgenstein è certamente che questa sbarra serve
come campione di lunghezza e quindi non possiamo attribuirle una lunghezza.
Sia come sia (potrebbe non essere così), è l’asserto “La sbarra S è lunga un
metro” una verità necessaria? Ovviamente la sua lunghezza può variare nel
tempo. Potremmo rendere più precisa la definizione stipulando che un metro
sia la lunghezza di S al tempo fissato t0. E allora una verità necessaria che la
sbarra S sia lunga un metro al tempo t0? Chi è convinto che tutto ciò che si sa a
priori è necessario potrebbe dire: “Questa è la definizione di metro. Per
definizione, la sbarra S è lunga un metro a t0. Si tratta di una verità necessaria.”
4
Ma a me pare che non ci sia nessuna ragione di arrivare a questa conclusione,
neppure per chi usa la suddetta definizione di “un metro”. Infatti costui sta
usando la definizione non per dare il significato di ciò che ha chiamato il
“metro”, ma per fissarne il riferimento. (Per una cosa tanto astratta come
un’unità di misura, la nozione di riferimento può non essere chiara. Ma
supponiamo che lo sia abbastanza per i presenti scopi.) Egli la usa dunque per
fissare un riferimento. C’è una certa lunghezza che egli vuole contrassegnare e
la contrassegna con una proprietà accidentale, cioè che esiste una sbarra di
quella lunghezza. Qualcun altro potrebbe contrassegnare lo stesso riferimento
con un’altra proprietà accidentale. Ma in ogni caso, anche se egli se ne serve per
fissare il riferimento del suo campione di lunghezza, un metro, può tuttavia
dire: “Se si fosse riscaldato questa sbarra S a t0, allora a t0 la sbarra S non
sarebbe stata lunga un metro.”
Ebbene, perché costui lo può fare? In parte, è possibile trovarne la ragione in
certe posizioni della filosofia della scienza, in cui non voglio entrare in questa
sede. Ma una risposta semplice alla domanda è questa: anche se questo è l’unico
campione di lunghezza che egli usa, c’è una differenza intuitiva tra l’espressione
“un metro” e l’espressione “la lunghezza di S a t0”. Con la prima espressione si
intende designare rigidamente una certa lunghezza in tutti i mondi possibili, che
nel mondo reale capita che sia la lunghezza della sbarra S a t0. D’altra parte, “la
lunghezza di S a t0” non designa nulla rigidamente. In alcune situazioni
controfattuali la sbarra avrebbe potuto essere più lunga e in altre più corta, se
fosse stata sottoposta a varie pressioni e tensioni. Così di questa sbarra, proprio
come di qualunque altra della stessa sostanza e della stessa lunghezza, possiamo
dire che se fosse stata riscaldata in una certa misura si sarebbe espansa di una
certa lunghezza. Un asserto controfattuale del genere, in quanto è vero dì altre
sbarre con identiche proprietà fisiche, sarà vero anche di questa. Non c’è
conflitto tra quell’asserto controfattuale e la definizione di “un metro” come “la
lunghezza di S a t0”, poiché la “definizione”, bene interpretata, non dice che
l’espressione “un metro” debba essere sinonima (anche qualora si parli di
situazioni controfattuali) dell’espressione “la lunghezza di S a t0”, ma piuttosto
che abbiamo determinato il rif erimmto dell’espressione “un metro” stipulando
che “un metro” debba essere un designatore rigido della lunghezza che di fatto
è quella di S a t0. Non per questo diventa una verità necessaria il fatto che S sia
lunga un metro a t0. Anzi, in certe circostanze S non sarebbe stata lunga un
metro. La ragione di ciò sta nel fatto che un designatore (“un metro”) è rigido
mentre l’altro (“la lunghezza di S a t0”) non lo è.
Qual è allora lo status epistemologico dell’asserto “La sbarra S è lunga un
metro a t0”, per chi abbia fissato il sistema metrico facendo riferimento a S?
Sembrerebbe che egli lo conosca a priori. Infatti, se ha usato la sbarra S per
fissare il riferimento del termine “un metro”, allora come risultato di questo
tipo di “definizione” (che non è una definizione abbreviativa o sinonimica) egli
sa automaticamente senza ulteriori ricerche che S è lunga un metro. D’altra
parte, anche se S viene usata come metro campione, lo status metafisico di “S è
lunga un metro” sarà quello di un asserto contingente, purché si consideri “un
metro” come un designatore rigido: sotto opportune tensioni e pressioni,
riscaldamenti o raffreddamenti, S avrebbe avuto una lunghezza diversa da un
metro anche a to. (Può avere uno status analogo anche un asserto come
“L’acqua bolle a 100°C al livello del mare”.) In questo senso dunque ci sono
verità a priori contingenti. Ancor più importante per i nostri scopi che prendere
questo esempio come un caso di contingente a priori, è il fatto che esso illustra
la distinzione tra “definizioni” che fissano un riferimento e definizioni che
danno un sinonimo.
5
…
Qualcuno potrebbe conoscerla a priori in un certo senso, se di fatto fissasse il
riferimento di “Aristotele” come l’uomo che fece una di queste cose. Ma
ancora non sarebbe per lui una verità necessaria. Quindi un esempio di questo
tipo sarebbe un esempio di come l’apriorità non implichi necessariamente la
necessità, se fosse corretta la teoria dei nomi come agglomerati. L’esempio del
fissare il riferimento di “un metro” è un esempio molto chiaro di come
qualcuno, solo per il fatto di aver fissato il riferimento in quel modo, può in un
certo senso sapere a priori che la lunghezza di questa sbarra è di un metro
senza considerarlo come una verità necessaria. Forse la tesi per cui l’apriorità
implica La necessità può essere modificata. Sembra che essa esprima
un’intuizione che potrebbe essere importante e vera sull’epistemologia. In un
certo senso un esempio come questo può sembrare un controesempio banale
che tuttavia in realtà non tocca ciò che si ha in mente quando, come fanno
alcuni, si pensa che solo Le verità necessarie possono essere note a priori.
Ebbene, se la tesi per cui tutte le verità a priori sono necessarie deve essere
immune da questo tipo di controesempi, essa va comunque modificata,
altrimenti porta a una confusione sulla natura del riferimento. E per conto mio
non ho alcuna idea di come andrebbe riformulata o modificata o se una
modifica o riformulazione del genere sia possibile.
…
Analogamente, anche se definiamo che cos’è un metro facendo riferimento al
metro campione, sarà una verità contingente e non una verità necessaria il fatto
che quella particolare sbarra sia lunga un metro: se fosse stata sottoposta a
tensione, sarebbe stata più lunga di un metro. Questo perché usiamo il termine
‘un metro’ per designare rigidamente una certa lunghezza. Anche se fissiamo la
lunghezza che vogliamo designare mediante una sua proprietà accidentale,
proprio come nel caso del nome di una persona scegliamo la persona mediante
una sua proprietà accidentale, tuttavia usiamo il nome per designare quella
persona o quella lunghezza in tutti i mondi possibili.
Circa chi ha ragione, se W o Kripke, vorrei dire che una cosa è lunga un
metro se è lunga come il metro standard e il metro standard è certamente
lungo come il metro standard. Questa è un’argomentazione diversa da
quella di Kripke. Del resto dire che qualcosa è lunga quanto è lunga non dà
nessuna vera informazione, come non la dà dire che qualcosa è identica a se
stessa. La seconda è una verità logica, la prima quasi, e lo diventa se
diciamo che la lunghezza di m è identica alla lunghezza di m. Il punto è che
se per definizione (coordinativa) la lunghezza di m è 1 metro, allora, ne
ricaviamo che la lunghezza di m è un metro, che non è una verità logica,
perché abbiamo assunta una definizione che non è una definizione logica.
L’idea di Schlick, rielaborata, credo possa essere usata, via Kripke, per
spiegare come si istituisce il significato di una parola. Ci torneremo su.
Somiglianze di famiglia e concetti.
6
Da H. Glock A Wittgenstein Dictionary (Oxford Blackwell 1996), p. 121:
Da P. Violi Significato ed esperienza (Milano Bompiani 1997), p. 178.
E. Rosch and C. Mervis “Family Resemblances: Studies in the Internal Structure of Categories”
(Cognitive Psychology 7 1975: 573-605).