Rappresentazione
dell’informazione
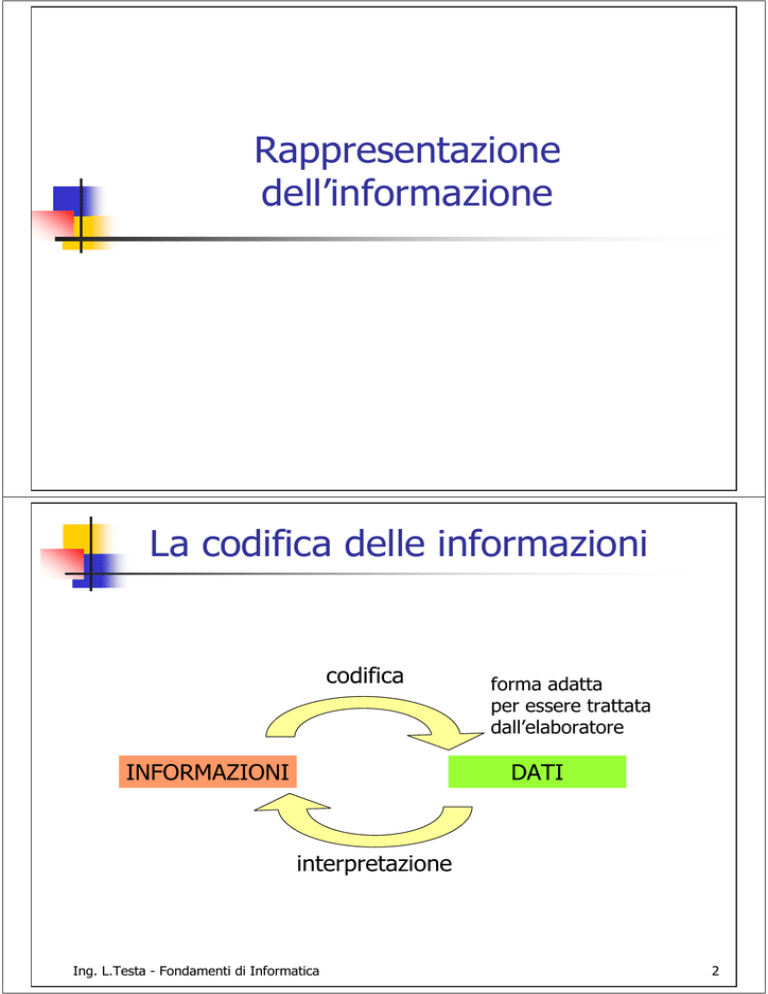
La codifica delle informazioni
codifica
INFORMAZIONI
forma adatta
per essere trattata
dall’elaboratore
DATI
interpretazione
Ing. L.Testa - Fondamenti di Informatica
2
Informazioni
Numeri
Interi positivi
Positivi e negativi
Reali
Testi
Informazioni tradizionali
Immagini fisse
Vettoriali
Bitmap
Audio
Video
Informazioni multimediali
Ing. L.Testa - Fondamenti di Informatica
Rappresentazione dell’informazione
Interessa soprattutto distinguere informazioni
diverse
Con un solo simbolo è impossibile
Pertanto l’insieme minimo è costituito da
2 simboli (alfabeto binario)
Ing. L.Testa - Fondamenti di Informatica
Rappresentazione dell’informazione
Le informazioni vengono rappresentate mediante
sequenze di simboli
Nel caso dei simboli binari, le informazioni
(numeri, oggetti, parole) sono rappresentate da
sequenze dei due simboli (0 e 1)
Servono regole di manipolazione dei simboli
Ing. L..Testa Fondamenti di Informatica
Sistemi numerici
5
Sistemi numerici
Per determinare un sistema numerico serve:
un insieme limitato di simboli (le cifre), che
rappresentano quantità prestabilite (1, 2, V, X,
M)
le regole per costruire i numeri:
sistemi numerici posizionali
sistemi numerici non posizionali
Ing. L.Testa - Fondamenti di Informatica
Sistemi numerici
Sistemi numerici non posizionali:
valore delle cifre è indipendente dalla posizione
Sistemi numerici posizionali:
il valore delle cifre dipende dalla loro posizione
all’interno del numero
(ogni posizione ha un peso)
Ing. L.Testa - Fondamenti di Informatica
Sistemi numerici posizionali
Esempio:
N = d3 d2 d1 d0 ; V(N) = d3*p3 + d2*p2 + d1*p1 + d0*p0
N Æ rappresentazione del numero
V(N) Æ valore del numero
Sistemi a base fissa:
pi = ri
dove:
r è la base del sistema
di rappresentano le cifre
Ing. L.Testa - Fondamenti di Informatica
Sistemi posizionali a base fissa
N = dn-1 dn-2 … d1 d0
V(N) = dn-1*rn-1 + dn-2*rn-2 + … + d1*r1 + d0*r0
Proprietà
È a rango illimitato (ogni numero intero vi può
essere rappresentato)
È a rappresentazione unica (ad ogni numero
intero corrisponde un solo insieme ordinato di cifre)
È irridondante (ad ogni insieme ordinato di cifre
corrisponde un solo numero non rappresentato da altri
insiemi ordinati)
Ing. L.Testa - Fondamenti di Informatica
Sistema decimale
È un sistema numerico posizionale a base fissa
Il sistema decimale utilizza:
r = 10
d = 0,1,2,3,4,5,6,7,8,9
Ing. L.Testa - Fondamenti di Informatica
Sistema decimale
8427
=
8*103 + 4*102 + 2*101 + 7*100
Ing. L.Testa - Fondamenti di Informatica
Sistema binario
Anche il sistema binario è un sistema numerico
posizionale a base fissa
Il sistema binario utilizza:
r = 2
d = 0,1
Ogni cifra è detta bit (da BInary digiT)
Ing. L.Testa - Fondamenti di Informatica
Sistema binario
1011 = 1*23 + 0*22 + 1*21 + 1*20 = 1110
Ing. L.Testa - Fondamenti di Informatica
Altri sistemi utilizzati
Sistema ottale:
r = 8
d = 0,1,2,3,4,5,6,7
Sistema esadecimale:
r = 16
d = 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Ing. L.Testa - Fondamenti di Informatica
Conversioni di base
Dal sistema binario a quello decimale
Utilizzando la definizione:
10102 = (1*8 + 0*4 + 1*2 + 0*1)10 =
= (8+2)10 = 1010
Oppure si può utilizzare il seguente formato:
N = ((dn-1*r + dn-2)*r + dn-3) …)*r + d0
Ing. L.Testa - Fondamenti di Informatica
1
Conversioni di base
Dal sistema decimale a quello binario
Esempio: 11510 = 1110011 2:
115
1
d0
d1
2
57
1
2
28
0
d2
2
14
0
d3
2
7
1
d4
2
3
1
d5
2
1
1
d6
Ing. L.Testa - Fondamenti di Informatica
Numeri frazionari
E’ possibile anche rappresentare numeri frazionari:
le potenze variano anche nel campo negativo
V(N) =
Σi di*ri = dn-1*rn-1 +…+ d0*r0 + d-1*r-1 +…+ d-m*r-m
N = dn-1 dn-2 … d1 d0 . d-1 d-2 … d-m+1 d-m
Ing. L.Testa - Fondamenti di Informatica
2
0
Conversioni di base
(per numeri frazionari)
Dal sistema binario a quello decimale
Sempre utilizzando la definizione:
0.1012 = 0*20 + 1*2-1 + 0*2-2 + 1*2-3=
= (0.5+0.125)10 = 0.62510
Ing. L.Testa - Fondamenti di Informatica
Conversioni di base
(per numeri frazionari)
Dal sistema decimale a quello binario
Esempio: 0.62510 = 0.101 2:
0.625 *
2
1.250 *
2
0.500 *
2
1.000
Ing. L.Testa - Fondamenti di Informatica
0.62510 = 0.101
2
Conversioni di base
Dal sistema decimale a quello binario
N.B.: Per convertire un numero composto da una parte
intera e una frazionaria in un altro sistema numerico,
occorre convertire separatamente le due parti e
successivamente giustapporre.
Ing. L.Testa - Fondamenti di Informatica
Conversione da binario ad esadecimale
100010112
1000 1011
8Bh
Ing. L.Testa - Fondamenti di Informatica
16 = 24 !!!
Numero di cifre necessario
Le macchine hanno vincoli spaziali:
è necessario conoscere il massimo valore
rappresentabile:
con n bit si può rappresentare al massimo il
numero 2n -1
è facile determinare che
n = INT( log2 (X+1) )
Ing. L.Testa - Fondamenti di Informatica
Operazioni aritmetiche
Per effettuare operazioni è necessario conoscere
la definizione del comportamento per ogni coppia
di simboli
Per ogni operazione esiste una tabella
Ing. L.Testa - Fondamenti di Informatica
Somma binaria
La tabella di definizione è:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0
con riporto di 1
1 + 1 + 1 = 1
con riporto di 1
Esempi
Ing. L.Testa - Fondamenti di Informatica
Sottrazione binaria
La tabella di
0 - 0
=
1 - 0
=
1 - 1
=
0 - 1
=
definizione è:
0
1
0
1
con prestito di 1 dal
bit di peso superiore
Esempi
Ing. L.Testa - Fondamenti di Informatica
Moltiplicazione e divisione
Si utilizzano le stesse procedure:
per la moltiplicazione:
somma e scorrimento
per la divisione:
differenza e scorrimento
Esempi
Ing. L.Testa - Fondamenti di Informatica
Rappresentazione dei numeri
nei calcolatori
Rappresentazione dei numeri nei calcolatori
Esiste un limite al numero di bit impiegati per
rappresentare un numero
Tale limite dipende da:
intervallo di variabilità
occupazione di memoria
Ing. L.Testa - Fondamenti di Informatica
Overflow e Underflow
Sono condizioni in cui si ha un errore nella
rappresentazione del risultato
Generalmente la rappresentazione è formata da
un numero finito di bit: se si supera tale limite si
ha errore
Ing. L.Testa - Fondamenti di Informatica
Numeri positivi
La rappresentazione di numeri positivi non crea
problemi
Si può avere overflow se il risultato delle
operazioni richiede un numero maggiore di bit di
quanto disponibile
Esempio: somma modulo 16
Ing. L.Testa - Fondamenti di Informatica
Numeri negativi
Esistono diverse possibilità di rappresentazione:
modulo e segno
complemento a 2
n
Ing. L.Testa - Fondamenti di Informatica
Modulo e segno
Convenzione per il bit più significativo:
0 : segno positivo
1 : segno negativo
esistono due rappresentazioni per lo ‘0’
+ 5 ---> 00101
- 10 ---> 11010
+ 0 ---> 00000
- 0 ---> 10000
Ing. L.Testa - Fondamenti di Informatica
Complemento a 2
(complemento alla base)
Dato X in base r di n cifre:
rn – X (complemento alla base del numero X)
Se X=01011, r=2, n=5
25-X = 100000 – 01011 = 10101
Regoletta pratica: il complemento a 2 si trova analizzando i bit del
numero a partire da destra: si riportano invariati tutti gli zeri fino al
primo bit a 1, si riporta invariato questo stesso bit a 1, si
complementano (0Æ1, 1Æ0) tutti gli altri bit
Ing. L.Testa - Fondamenti di Informatica
Complemento a 2
complemento a 2:
(complemento alla base)
per definizione il complemento a 2 di X è 2n - X
unica rappresentazione dello ‘0’
I numeri positivi sono rappresentati dal loro modulo e hanno il
bit più significativo (segno) posto a zero. I numeri negativi sono
rappresentati dal complemento a 2 del corrispondente numero
positivo, segno compreso. Pertanto, i numeri negativi hanno il
bit più significativo sempre a 1.
Esempio:
+3 <=> 00011
- 3 <=> 11101
Ing. L.Testa - Fondamenti di Informatica
Uso dei numeri negativi
Modulo e segno:
la somma algebrica di numeri positivi e negativi
può generare problemi
servono sistemi hardware specifici per la
gestione corretta del formato
Complemento a due:
la somma algebrica non genera problemi
Ing. L.Testa - Fondamenti di Informatica
Complemento a 2
Motivazione:
Sia dato un numero di bit n
i numeri che si possono rappresentare sono
n
nel range [0 - 2 -1]
si vuole calcolare A-B
n
si sostituisce -B con (2 -B)
n
si ottiene A+(2 -B)
La sottrazione si esegue mediante una somma!
Ing. L.Testa - Fondamenti di Informatica
Numeri negativi:
intervallo valori rappresentabili
Rappresentazione modulo e segno
-2n-1 + 1 ≤ N ≤ 2n-1 - 1
Rappresentazione in complemento a due
-2n-1 ≤ N ≤ 2n-1 - 1
Ing. L.Testa - Fondamenti di Informatica
Rappresentazione numeri reali
I numeri reali sono nel range [-∞ ÷ +∞]
Talvolta è necessaria una rappresentazione estesa
sulla retta dei reali
con 3 simboli
[+/-], X, Y, Z ∈ {0,1,…9} è
possibile rappresentare -999 ÷ +999
oppure
9 * 10[+/-] 99
[+/-] 99
oppure [+/-] 9 * 10
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
E’ la risposta alla necessità di manipolare
numeri di ordini di grandezza diversi
Notazione scientifica - numeri espressi nella forma:
X.YYY * 10WW
X: parte intera
Y: parte frazionaria
W: esponente
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
Nomenclatura:
A = M * BE
M: mantissa
B: base
E: esponente
Necessita di un segno per la mantissa e uno per
l’esponente
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
Forma normalizzata:
numero = ± 1.XXXXXXX * 2a
.XXXXXXX parte frazionaria
a è detto esponente vero
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
Rappresentazione standard (IEEE P754)
Segno: 1 bit di segno (0 per i positivi, 1 per i negativi)
Esponente: l’esponente vero è rappresentato come
numero senza segno su 8 bit usando la
rappresentazione eccesso 127 (il valore che quindi si
rappresenta è a+127; il valore dell’esponente vero
dovrà essere in modulo minore di 127)
Mantissa: vengono rappresentati i primi 23 bit della
parte frazionaria della forma normalizzata (hidden bit :
la parte intera di peso 20 viene sottintesa)
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
Rappresentazione IEEE P754 (32 bit)
1 bit per il segno
8 bit per l’esponente (rappresentazione eccesso 127)
23 per la mantissa (parte frazionaria - normalizzata)
Segno Esponente
S
E
Mantissa
F
N = (-1)S * 2E-127 * 1.F
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile - precisione
S
(1 bit)
E
(8 bit)
F
(23 bit)
32 bit (singola precisione), M=127
S
(1 bit)
E
(11 bit)
F
(52 bit)
64 bit (doppia precisione), M=1023
S
(1 bit)
E
(15 bit)
F
(112 bit)
128 bit (quadrupla precisione), M=16383
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
Esempi usando: B=10, 2 cifre all’esponente e 8
alla mantissa:
+1
0 01 10000000
-63517,8
1 05 63517800
-0,000635178 1 97 63517800
-8,75 * 10-13 1 88 87500000
Fondamenti di Informatica
46
Virgola mobile
Moltiplicazione e divisione:
si moltiplica o si dividono le mantisse in
modo consueto
si sommano o si sottraggono gli esponenti
si normalizza
Esempio: 10,4 * 200 =
0 02 10400000 * 0 03 20000000 =
0 05 20800000
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
Somma e sottrazione:
si uguagliano gli esponenti
le mantisse vengono sommate
aggiustamento in caso di traboccamento
Esempio: 10,4 + 2 =
0 02 10400000 + 0 01 20000000 =
0 02 10400000 + 0 02 02000000 =
0 02 12400000 = 12,4
Ing. L.Testa - Fondamenti di Informatica
Virgola mobile
Approssimazioni:
34,56 + 0,005 =
0 02 3456 + 0 98 5000 =
0 02 3456 + 0 02 0000 =
0 02 3456 = 34,56
La precisione è data dal numero di cifre della
mantissa:
Doppia precisione: doppia lunghezza della
mantissa (range invariato, precisione raddoppiata)
Ing. L.Testa - Fondamenti di Informatica
Memorizzazione su calcolatore
e codici
Memorizzazione su calcolatore
L'unità atomica è il bit (BInary DigiT)
L'insieme di 8 bit è detta byte
Altre forme di memorizzazione:
Word (16 bit)
Double-word (32 bit)
Quad-word (64 bit)
Ing. L.Testa - Fondamenti di Informatica
Intervalli di variabilità
bit:
Numero di configurazioni: 2
intervallo di variabilità: [0-1]
byte:
Numero di configurazioni: 256
intervallo di variabilità:
dipende dal tipo di memorizzazione
Ing. L.Testa - Fondamenti di Informatica
Tipi di memorizzazione
Modulo: 256 configurazioni,
[0, 255]
Modulo e segno: 256 configurazioni,
[-127, +127]
Complemento a 2: 256 configurazioni,
[-128, +127]
Ing. L.Testa - Fondamenti di Informatica
Intervalli di variabilità
Word:
Double-word: [0, 232-1]
Quad-word:
Ing. L.Testa - Fondamenti di Informatica
[0, 216-1]
[0, 264-1]
Convenzioni
Floating point:
mantissa: 23 bit
segno: 1 bit
esponente: 8 bit
Ing. L.Testa - Fondamenti di Informatica
Codici
Codice: sistema di simboli che permette la
rappresentazione dell’informazione
0
Esempi:
Decodifica agevole vs codici compressi
Ing. L.Testa - Fondamenti di Informatica
Definizioni
SIMBOLO: entità di cui non si da qui una
definizione formale
STRINGA: sequenza finita di simboli
giustapposti (lunghezza della stringa, stringa
vuota)
ALFABETO: insieme finito di simboli
LINGUAGGIO: insieme di stringhe di simboli
tratti da un alfabeto
Ing. L.Testa - Fondamenti di Informatica
Esempi di alfabeti
Alfabeto italiano:
{A, B, C, D, …Z}
Alfabeto greco:
{α, β, γ, δ, ...ω}
Alfabeto binario:
{0, 1}
Ing. L.Testa - Fondamenti di Informatica
Alfabeto usato dal calcolatore
Interruttore (aperto/chiuso)
Foro su scheda (aperto/chiuso)
Transistor (in conduzione/spento)
Tensione (alta/bassa)
Dominio di magnetizzazione (↑/↓)
Riflettività di un’areola (alta/bassa)
Ing. L.Testa - Fondamenti di Informatica
Alfabeto usato dal calcolatore
Gli elaboratori utilizzano una logica e un’aritmetica
binaria
Ai due stati di un dispositivo vengono associati i
due simboli 0 e 1
Ing. L.Testa - Fondamenti di Informatica
Codifica dei simboli
E’ necessario determinare delle regole di
corrispondenza, dette codifiche
La codifica mette in corrispondenza (biunivoca)
ogni simbolo appartenente all’alfabeto più ricco
con una stringa di simboli appartenente
all’alfabeto più ridotto.
Ing. L.Testa - Fondamenti di Informatica
Codifica
Problema:
codificare i simboli dell’alfabeto A utilizzando
stringhe del linguaggio L, con A qualsiasi e
L={ stringhe di N bit }
Cardinalità C dell’alfabeto A:
numero di elementi di A
Ing. L.Testa - Fondamenti di Informatica
Codifiche ridondanti
Se C e’ la cardinalità, si deve avere:
N ≥ log2 C = M
cioè:
se
se
C ≤ 2N
M⎤ =N
M⎤ <N
è senza ridondanza
è con ridondanza
Ing. L.Testa - Fondamenti di Informatica
Distanza di Hamming
E’ definita come il minimo numero di bit di cui
differiscono due parole qualsiasi del codice
se N=M
si ha che
se c’è ridondanza,
Ing. L.Testa - Fondamenti di Informatica
H=1
H≥1
Rilevazione e correzione di errori
La ridondanza può servire per rilevare o
correggere errori nel codice
Num di errori rilevati: R = H-1
Num di errori corretti:
H −1
C≤
2
Ing. L.Testa - Fondamenti di Informatica
Esempio di codifica ridondante
Parità:
si ottiene dal codice non ridondante aggiungendo
un simbolo in modo che il numero di ‘1’ sia pari
(parità pari) o dispari (parità dispari).
Avendo H=2 può solo rilevare un errore
Ing. L.Testa - Fondamenti di Informatica
Codice BCD
BCD: Binary Coded Decimal
Simbolo: Codifica:
0
1
2
3
4
8
9
…
0000
0001
0010
0011
0100
1000
1001
Ing. L.Testa - Fondamenti di Informatica
Operazioni sui BCD
E’ usato spesso quando l’elaborazione è ridotta,
mentre la visualizzazione è frequente
Problema della correzione (+6)
Ing. L.Testa - Fondamenti di Informatica
Codifica dei testi
Si utilizza una tabella (arbitraria)
Standard oggi (quasi) universalmente riconosciuto
Codice ASCII
American Standard Code for Information Interchange
Ing. L.Testa - Fondamenti di Informatica
Codice ASCII
Si utilizzano 7 bit
quindi
128 simboli diversi
ASCII esteso (8bit)
diverse estensioni in dipendenza dal paese
oppure aggiunge la parità
Ing. L.Testa - Fondamenti di Informatica
Codice ASCII
Ing. L.Testa - Fondamenti di Informatica
Codice ASCII - note
I caratteri alfabetici sono consecutivi e in ordine
(alfabetico)
La distanza tra una lettera minuscola e la
corrispondente maiuscola è costante
Le cifre decimali sono consecutive e in ordine
(da 0 a 9)
Ing. L.Testa - Fondamenti di Informatica