Propagazione di Raggi Cosmici di Energie Ultra Alte provenienti da

Università degli Studi di L’Aquila
Facoltà di Scienze Matematiche Fisiche e Naturali
Corso di Laurea Specialistica in Fisica
Tesi di Laurea
Propagazione di Raggi Cosmici di
Energie Ultra Alte provenienti da
sorgenti extragalattiche.
Simulazioni con sorgenti da cataloghi,
studio delle anisotropie risultanti e
confronto con i dati di Auger.
Relatori:
Candidato:
Prof. Aurelio Grillo
Denise Boncioli
Dott. Roberto Aloisio
Anno Accademico 2007-2008
Indice
1 Modelli di produzione di raggi cosmici
1.1 Accelerazione di Fermi al II ordine . .
1.2 Shock . . . . . . . . . . . . . . . . . .
1.3 Accelerazione da shock . . . . . . . . .
1.3.1 Spettro . . . . . . . . . . . . .
1.3.2 Energia massima . . . . . . . .
.
.
.
.
.
2 Sorgenti di raggi cosmici ultra-energetici
2.1 Supernovae . . . . . . . . . . . . . . . .
2.1.1 Esplosione di Supernovae . . . . .
2.1.2 Accelerazione in Supernovae . . .
2.2 Nuclei galattici attivi . . . . . . . . . . .
2.2.1 Unificazione degli AGN . . . . . .
2.2.2 Accelerazione in AGN . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
. 7
. 9
. 10
. 12
. 13
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
17
17
19
20
21
25
27
3 Propagazione di raggi cosmici
3.1 Perdite di energia . . . . . . . . . . . . . . . . . . . . . . .
3.1.1 Caratteristiche dell’interazione tra protoni e CMBR
3.2 Evoluzione cosmologica . . . . . . . . . . . . . . . . . . . .
3.3 Spettro degli UHECR . . . . . . . . . . . . . . . . . . . .
3.3.1 Spettro di singola sorgente . . . . . . . . . . . . . .
3.3.2 Spettro da distribuzioni di sorgenti . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
35
35
38
40
42
42
45
4 Esperimenti
4.1 Air Showers . . . . . . . . . . . . . . . . .
4.1.1 Composizione . . . . . . . . . . . .
4.1.2 Struttura spaziale . . . . . . . . . .
4.1.3 Struttura temporale . . . . . . . .
4.1.4 Direzione . . . . . . . . . . . . . .
4.2 Caratteristiche del raggio cosmico primario
4.2.1 Composizione chimica . . . . . . .
4.2.2 Energia . . . . . . . . . . . . . . .
4.3 Accettanza . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
49
49
50
51
54
55
56
56
57
58
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4.4
Esperimenti . . . . . . .
4.4.1 AGASA . . . . .
4.4.2 Fly’s Eye e HiRes
4.4.3 Auger . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
59
59
59
60
5 Anisotropia
5.1 Evidenze di anisotropia degli UHECR . . . . . .
5.1.1 Correlazione con Nuclei Galattici Attivi
5.1.2 Angular power spectrum . . . . . . . . .
5.1.3 Mappe di densità . . . . . . . . . . . . .
5.2 Discussione sui risultati di Auger . . . . . . . .
5.3 Cataloghi alternativi . . . . . . . . . . . . . . .
5.3.1 Swift BAT AGN Catalog . . . . . . . . .
5.3.2 Correzioni al catalogo VCV . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
66
67
68
71
73
74
77
77
78
.
.
.
.
.
.
81
82
83
85
89
91
94
6 Risultati
6.1 Spettro di Auger . . . . . . . . . . . . . . . . . . .
6.2 Spettro teorico . . . . . . . . . . . . . . . . . . . .
6.2.1 Calcolo del flusso da sorgenti discrete . . . .
6.2.2 Calcolo del flusso da distribuzione uniforme
6.3 Parametri del flusso . . . . . . . . . . . . . . . . . .
6.4 Calcolo del flusso teorico totale . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A Coefficiente di diffusione
106
B Coordinate galattiche
109
C Esposizione
111
D Magnitudine e Luminosità
112
D.1 Luminosità assoluta . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
D.2 Luminosità bolometrica . . . . . . . . . . . . . . . . . . . . . . . . . . 113
Bibliografia
114
2
Introduzione
I raggi cosmici sono principalmente costituiti da particelle cariche molto enegetiche
che bombardano la terra; lo spettro energetico che si osserva si estende da energie
di 109 eV fino a 1021 eV.
Lo studio dei raggi cosmici comincia agli inizi del 1900 attraversando varie tappe
fino alla conferma da parte di Pierre Auger, nel 1938, dell’esistenza degli sciami
atmosferici estesi (EAS), ovvero cascate di particelle secondarie e nuclei prodotti
dalla collisione di particelle primarie di alta energia con le molecole dell’atmosfera.
L’esistenza degli EAS permette lo studio indiretto dei raggi cosmici primari ad
alte energie, attraverso il campionamento delle particelle secondarie sul suolo terrestre; la fisica dei raggi cosmici si avvale inoltre dell’atmosfera come scintillatore
naturale. Nel loro passaggio attraverso l’atmosfera le particelle dello sciame eccitano
le molecole di azoto in essa presenti che emettono successivamente luce di fluorescenza; la raccolta di questa emissione permette una stima dell’energia del primario.
Esistono diversi esperimenti attualmente funzionanti che sfruttano sia il campionamento delle particelle a terra che la raccolta della luce di fluorescenza, nel
tentativo di studiare i raggi cosmici alle energie più alte e di capirne l’origine.
Investigando sull’origine dei raggi cosmici, un punto di partenza può essere la
considerazione del fatto che, essendo i raggi cosmici particelle cariche, affinchè queste
possano essere accelerate è necessaria la presenza di un campo elettrico. Sappiamo
che in astrofisica non esistono campi elettrici statici ma esistono campi elettrici dinamici prodotti da campi magnetici variabili; campi elettrici di questo tipo esistono
per esempio nelle stelle di neutroni.
E’ possibile inoltre, rimanendo sempre nell’ambito dell’origine astrofisica dei raggi cosmici, spiegare il raggiungimento di alte energie di queste particelle cariche
attraverso meccanismi che prevedono l’interazione delle particelle con i campi magnetici irregolari presenti nei plasmi astrofisici.
Attraverso il meccanismo dell’accelerazione da onde d’urto che si generano nell’esplosione di supernovae galattiche si può infatti giustificare lo spettro dei raggi
cosmici fino a energie di circa 1017 eV; confrontando il raggio di Larmor della particella e le dimensioni della regione in cui è presente il campo magnetico è possibile
fornire un limite superiore all’energia raggiungibile in processi di accelerazione, identificando quindi una serie di oggetti astrofisici che, per intensità del campo magnetico
presente e dimensioni, sono da considerarsi potenziali sorgenti di raggi cosmici.
3
In ambiente galattico le possibili sorgenti di raggi cosmici sono resti di supernovae e stelle di neutroni; nel caso di energie superiori a circa 1017 eV non esistono
sorgenti galattiche in grado di accelerare particelle a tali energie. Si prendono quindi in considerazione oggetti extragalattici, in particolare le galassie che ospitano un
nucleo attivo, ovvero una struttura alimentata da un buco nero centrale molto massivo.
In questo lavoro di Tesi sono state prese in esame le teorie basate sull’origine dei
raggi cosmici in sorgenti astrofisiche; in particolare gli oggetti candidati a sorgenti
di raggi cosmici qui considerati sono proprio i nuclei galattici attivi (AGN).
Premesso che non è semplice trovare sorgenti con caratteristiche tali da portare
protoni a energie superiori a 1020 eV, un ulteriore problema per l’osservazione di
questi eventi è dato dalla propagazione; nel tragitto dalla sorgente all’atmosfera
terrestre le particelle di raggi cosmici risentiranno delle varie interazioni con i fotoni della radiazione cosmica di fondo (CMBR) e con altri fondi astrofisici. Si deve
poi considerare, se prendiamo sorgenti extragalattiche, l’espansione dell’universo che
comporta una ulteriore perdita adiabatica di energia.
A questo si deve poi aggiungere l’interazione con i campi magnetici extragalattici e con il campo magnetico galattico; quest’ultimo può essere pensato come la
! = 3µG), su scala di 1 kpc, e
sovrapposizione di due componenti: una regolare (|B|
! = 2µG), su scala minore di 55 pc. Il campo magnetico galattico è
una casuale (|B|
inoltre responsabile della diffusione dei raggi cosmici di basse energie, cosa di cui si
ha evidenza dai tempi di permanenza di queste particelle nell’ambiente galattico e
dalla sostanziale isotropia della loro distribuzione di arrivo.
Nel caso dei raggi cosmici alle energie qui considerate, l’intensità del campo magnetico galattico non è in grado di defletterne la direzione per più di qualche grado.
Tornando all’interazione dei raggi cosmici con la CMBR, le perdite di energia dei
protoni sono dovute alla produzione di coppia e alla fotoproduzione di π; entrambi
questi processi sarebbero responsabili della forma dello spettro in energia dei raggi
cosmici, insieme all’iniezione delle particelle accelerate alla sorgente.
In particolare, a causa della reazione di fotoproduzione di π è prevista una soppressione del flusso di raggi cosmici a energie intorno a 7 × 1019 eV (effetto GreisenZatsepin-Kuz’min, detto GZK); nello spettro misurato dagli esperimenti Auger e
HiRes è evidente la presenza di un cut-off intorno all’energia 7 × 1019 eV.
Questa evidenza presa da sola non è però da considerarsi una verifica della previsione dell’effetto GZK in quanto mancano informazioni fondamentali riguardo alle
caratteristiche dei candidati a sorgenti, come l’energia massima a cui tali oggetti
possono accelerare particelle.
Se le sorgenti dei raggi cosmici più energetici sono relativamente vicine e non
sono uniformemente distribuite, allora ci possiamo aspettare una distribuzione di
arrivo anisotropa, se l’energia è sufficientemente alta da non deflettere in modo significativo la direzione di propagazione.
4
L’anisotropia dei raggi cosmici ad alte energie si può manifestare in due modi:
attraverso l’osservazione di un insieme di eventi ravvicinati da sorgenti individuali
o attraverso la correlazione delle direzioni di arrivo con un certo tipo di oggetti astronomici.
Gli AGN sono da lungo tempo considerati siti dove potrebbe avere luogo la produzione di particelle energetiche e dove queste particelle potrebbero essere accelerate
fino alle alte energie misurate.
I dati raccolti dall’esperimento Auger mostrano evidenza di una anisotropia nelle
direzioni di arrivo dei raggi cosmici alle energie più alte; queste direzioni sono state
quindi confrontate con le posizioni degli AGN, trovando una correlazione positiva
per raggi cosmici con energie maggiori di 6 × 1019 eV e AGN a distanze minori di
∼ 75 Mpc.
Le osservazioni risultano essere consistenti con l’ipotesi che la rapida decrescita
del flusso misurato dall’esperimento Auger oltre 6 × 1019 eV sia dovuto all’effetto
GZK e che la maggior parte dei raggi cosmici che raggiungono la Terra intorno a
queste energie siano protoni provenienti da sorgenti astrofisiche vicine, AGN o altri
oggetti con una simile distribuzione spaziale.
Sebbene questo risultato non identifichi in modo non ambiguo gli AGN con le
sorgenti di raggi comici a energie ultra alte, permette di pensare che questa identificazione sarà possibile con un set di dati più ampio, che l’Osservatorio Pierre Auger
garantirà in alcuni anni.
Con le informazioni raccolte sulla soppressione del flusso ad alte energie e sulla
correlazione trovata da Auger è interessante calcolare il flusso teorico di raggi cosmici da tali oggetti.
Il presente lavoro di Tesi rappresenta un modo per collegare le evidenze osservative offerte da Auger; il collegamento sta proprio nel calcolo dello spettro dei raggi
cosmici ultra-energetici (UHECR) e nel confronto con lo spettro sperimentale, utilizzando proprio le sorgenti in correlazione con gli eventi di UHECR. Vedremo in
seguito che a questo insieme di sorgenti discrete si deve aggiungere una componente
distribuita uniformemente che contribuisce al flusso da un certo redshift in poi.
Per la parte discreta di sorgenti sono stati utilizzati quindi gli AGN trovati in
correlazione con le direzioni degli eventi misurati in Auger (con redshift z ≤ 0.017),
calcolando il flusso in protoni a partire dalla luminosità dell’oggetto.
Per distanze maggiori è stata utilizzata una distribuzione uniforme di sorgenti; in
entrambi i contributi sono state considerate le perdite di energia dei protoni durante
la propagazione dalla sorgente all’atmosfera terrestre.
Inoltre è stato necessario fare delle diverse ipotesi sullo spettro delle particelle
alla sorgente, sia riguardo all’energia massima a cui le sorgenti sono in grado di
accelerare i protoni, sia riguardo all’indice dello spettro di iniezione. Lo spettro
ottenuto è stato poi confrontato con lo spettro misurato da Auger.
Il presente lavoro è organizzato come segue: nel primo capitolo sono presentati i
5
modelli di produzione di raggi cosmici che riguardano l’accelerazione in onde d’urto;
nel secondo capitolo si riportano alcune informazioni sulle sorgenti galattiche di raggi cosmici (Supernovae) e sulle sorgenti extagalattiche (Nuclei Galattici Attivi). In
particolare si parla degli AGN come siti di accelerazione extragalattici e si riportano
alcuni esempi di meccanismi di accelerazione in tali oggetti. Nel terzo capitolo si
introducono i processi fisici che condizionano la propagazione degli UHECR, con
particolare attenzione al calcolo del flusso atteso a Terra per protoni. Nel quarto
capitolo si presentano i principali risultati sperimentali sullo studio dei raggi cosmici in generale e le tecniche utilizzate per ottenerli, mentre nel quinto capitolo si
riportano le ricerche relative all’anisotropia dei raggi cosmici più energetici e i principali risultati dell’esperimento Auger. Infine, il sesto e ultimo capitolo è dedicato
al confronto tra lo spettro misurato da Auger e quello calcolato, con una discussione
sulle ipotesi fatte per il calcolo e le sorgenti utilizzate. Si riportano infine i possibili
sviluppi futuri di questo lavoro.
6
Capitolo 1
Modelli di produzione di raggi
cosmici
Le attuali teorie sulla produzione di raggi cosmici possono essere riunite in due
diversi scenari: lo scenario di accelerazione bottom-up e lo scenario di decadimento
top-down, con vari modelli entro ogni scenario.
Nella teoria bottom-up particelle cariche vengono accelerate da energie più basse
alle alte energie osservate in ambienti astrofisici; esistono infatti modelli che descrivono l’accelerazione di particelle in onde d’urto associate a resti di supernovae,
a nuclei galattici attivi e a galassie radio, oppure altri modelli che riguardano l’accelerazione in presenza di stelle di neutroni.
Nello scenario top-down le particelle più energetiche provengono dal decadimento
di particelle sufficientemente massive che hanno origine da processi fisici nell’universo primordiale; nell’ambito di queste teorie non sono quindi previsti meccanismi di
accelerazione.
Nel presente capitolo si analizzano i modelli di accelerazione di raggi cosmici che
riguardano le teorie bottom-up, riportando la versione dell’accelerazione di Fermi al
II ordine e l’accelerazione da shock, evidenziandone le differenze.
Si analizzano inoltre le caratteristiche dello spettro dei raggi cosmici che risulta
da questo tipo di accelerazione e i limiti sull’energia massima raggiungibile in ambito
astrofisico.
1.1
Accelerazione di Fermi al II ordine
Consideriamo una particella già accelerata a energie relativistiche, cioè con v ≈ c
e analizziamo il meccanismo di accelerazione delle particelle proposto inizialmente
da Fermi nel 1954.
Immaginiamo la particella, di energia E e impulso p nel sistema di riferimento
del laboratorio, che si muove verso una nube galattica, la quale si muove con velocità
−V lungo l’asse x, e θ è l’angolo che la velocità della particella forma con l’asse x. La
nube ha massa ≥ m (m massa della particella), quindi l’urto può essere considerato
7
elastico.
Nel sistema di riferimento della nube energia e impulso della particella sono dati
da:
E ! = γ (E + pV cos θ)
(1.1)
p!x
!
V
= γ p cos θ + 2 E
c
"
(1.2)
#
$−1/2
2
con γ = 1 − Vc2
. Avendo un urto elastico, l’energia e l’impulso della particella
dopo l’urto saranno:
E !! = E !
p!!x = −p!x .
(1.3)
(1.4)
Queste relazioni valgono nel sistema di riferimento della nube, mentre nel sistema
del laboratorio si avrà:
Ē = γ (E !! − V p!!x ) = γ (E ! + V p!x ) .
Sostituendo nell’equazione precedente le 1.1 e 1.2, troviamo:
!
"
2V v cos θ V 2
2
Ē = γ E 1 +
+ 2 ,
c2
c
(1.5)
(1.6)
dove abbiamo usato v cos θ/c2 = px /E, la velocità della particella nel sistema del
laboratorio. Quindi:
!
"
V v cos θ
V2
2
∆E = Ē − E = γ E 2
+2 2 ;
(1.7)
c2
c
poichè in generale V ≤ c, si può riscrivere l’equazione precedente in questo modo:
∆E
V v cos θ
V2
=2
+
2
.
E
c2
c2
(1.8)
Se in un sistema di questo tipo ci fossero urti frontali (cos θ = 1) si avrebbe un
guadagno di energia nel primo ordine in V /c; in realtà, le velocità delle nubi sono
distribuite in maniera casuale.
Il numero di urti per unità di tempo è proporzionale alla velocità
relativa
%
& (V cos θ + v);
θ
inoltre utilizzando il fatto che v ≈ c si avrà che P (cos θ) ∝ 1 + V cos
. A questo
c
punto, mediando su tutti i valori possibili di cos θ:
'
( ! " )1
! "2
x[1 + (V /c)x]dx
2V cos θ
2V
2 V
−1
=
=
,
(1.9)
)1
c
c
3 c
[1 + (V /c)x]dx
−1
8
dove x = cos θ.
Quindi, nel limite relativistico, il guadagno medio di energia per collisione è:
'
(
! "2
∆E
8 V
=
.
(1.10)
E
3 c
Il fatto che il processo sia al secondo ordine comporta innanzitutto che sia lento,
e inoltre che conduce a spettri con indici che possono assumere qualsiasi valore.
1.2
Shock
L’onda d’urto, o shock, rappresenta un tipo di discontinuità che costituisce una
superficie di separazione tra due fluidi con proprietà distinte, in cui però c’è un flusso
di massa, impulso ed energia attraverso la superficie stessa.
Consideriamo, per semplicità, una situazione a simmetria piana (tutte le quantità
dipendono solo da x, che è perpendicolare alla supeficie di discontinuità) e stazionaria.
Mettendosi in un riferimento comovente con tale superficie, ci vediamo venire
incontro con velocità u1 (diretta lungo x) un fluido con densità ρ1 e pressione P1 ;
applicando i principi di conservazione di massa, impulso ed energia si ottiene (in
x = 0):

ρ1 u1 = ρ2 u2
 cons. massa
cons. impulso ρ1 u21 + P1 = ρ2 u22 + P2
(1.11)
 cons. energia 1 ρ u2 + η u P = 1 ρ u2 + η u P
2 1 1
η−1 1 1
2 2 2
η−1 2 2
dove con η si indica il rapporto tra i calori specifici a pressione e volume costante
dei due fluidi.
Le relazioni scritte sopra (Rankine-Hugoniot) permettono di determinare le condizioni idrodinamiche del fluido dopo lo shock, quando sono note le condizioni prima
dello shock.
Definiamo ora il numero di Mach dello shock come il rapporto
M=
u1
cs1
(1.12)
tra la velocità con la quale lo shock si propaga nel mezzo imperturbato e la velocità
del suono nello stesso mezzo.
Per un fluido ideale vale la relazione:
u1
(η + 1)M21
ρ2
=
=
ρ1
u2
(η − 1)M21 + 2
(1.13)
che diventa, nel limite M1 → ∞ (shock forte):
u1
η+1
ρ2
=
=
.
ρ1
u2
η−1
9
(1.14)
Moto della particella attraverso la superficie dello shock; il tutto è visto nel
sistema di riferimento della superficie dello shock.
Figura 1.1:
Da qui si vede che nella regione perturbata (down-stream) si avrà un rallentamento
e un aumento della densità del gas rispetto alla regione imperturbata (up-stream):
u2 =
u1
, ρ2 = rρ1 ,
r
(1.15)
avendo posto r = η+1
; per un gas perfetto monoatomico si ha η = 53 , dunque r = 4.
η−1
Si ha inoltre che, sempre nel caso di shock supersonico, il gas imperturbato viene
riscaldato moltissimo, poichè si ha T2 /T1 ∝ M21 .
1.3
Accelerazione da shock
Nel paragrafo riguardante l’accelerazione di Fermi al II ordine abbiamo considerato l’accelerazione subita da una particella che incontra una nube di plasma in
moto, e viene quindi diffusa dal campo magnetico della nube.
Analizziamo ora il caso di una particella che incontra un fronte di shock in moto;
sia nell regione upstream che in quella downstream è presente un campo magnetico
turbolento (come nel caso della nube di Fermi). Quando la particella si trova nella
regione imperturbata, a causa della diffusione e del fatto che lo shock si muove,
sarà costretta ad attraversare lo shock; se invece si trova nell regione perturbata, il
fenomeno della diffusione farà sı̀ che la particella possa attraversare nuovamente lo
shock oppure allontanarsi dalla regione di accelerazione.
Consideriamo una test-particle (ovvero una particella che non perturbi lo shock)
che attaversa il fronte di shock da up a down, formando un angolo θi rispetto all’asse
x. Il fronte dello shock si muove con velocità −u1 , mentre il fluido down-stream si
10
allontana dallo shock con velocità u2 rispetto al fronte dello shock; quindi nel sistema del laboratorio si vede il fluido down-stream spostarsi nel verso negativo delle
x con V = u2 − u1 .
Scriviamo dunque l’energia della particella (che supponiamo relativistica) nel
sistema di riferimento down-stream:
!
"
V
!
Ei = ΓEi 1 − cos θi ,
(1.16)
c
% V &2 .−1/2
con Γ = 1 − c
.
La particella subirà una collisione nella regione down-stream, dopo la quale la
sua energia sarà Ef! nel sistema down-stream, e
Ef =
ΓEf!
!
V
1 + cos θf!
c
"
(1.17)
nel sistema up-stream.
Come nel caso dell’accelerazione di Fermi, l’energia si conserva dopo l’urto (Ef! =
Ei! ), quindi sostituendo:
!
"!
"
V
V
2
!
Ef = Γ Ei 1 + cos θf
1 − cos θi .
(1.18)
c
c
Il guadagno di energia sarà:
1 − β cos θi + β cos θf! − β 2 cos θi cos θf!
∆E
Ef − Ei
=
=
−1
Ei
Ei
1 − β2
(1.19)
dove β = V /c. Da notare che, nel caso dell’accelerazione di Fermi, si poteva avere
−1 ≤ cos θf! ≤ 1 e quindi si poteva sia guadagnare che perdere energia; nel caso del
fronte di shock, invece, si ha che cos θf! è sempre positivo e cos θi è sempre negativo,
quindi ∆E/E > 0 sempre.
A questo punto resta da mediare sugli angoli; sapendo che le distribuzioni di θf!
e θi rispetto al fronte dello shock sono rispettivamente:
dn
= 2 cos θf! , 0 ≤ cos θf! ≤ 1
d cos θf!
dn
= 2 cos θi , −1 ≤ cos θi ≤ 0
d cos θi
si ottiene:
ξ=
'
∆E
E
(
4
4 u1 − u2
= β=
.
3
3
c
11
(1.20)
(1.21)
1.3.1
Spettro
Supponiamo che una particella, dopo un ciclo di accelerazione, guadagni un’energia pari a:
∆E = E1 − E0 = ξE0
(1.22)
dove abbiamo visto che ξ = 43 β. Dopo il passaggio successivo attraverso il fronte di
shock, l’energia e il numero di particelle saranno dati da:
E2 = (1 + ξ)E1 = (1 + ξ)2 E0 ,
N2 = )N1 = )2 N0 ,
(1.23)
essendo (1 − )) la probabilità che la particella sfugga dalla regione down-stream.
All’n-esimo passaggio si avrà:
En = (1 + ξ)n E0 ,
quindi:
Nn = )n N0 ,
(1.24)
 # $
 ln Nn = n ln )
# N0 $
 ln En = n ln(1 + ξ)
E0
(1.25)
Eguagliando ora le due equazioni si ottiene:
ln
!
Nn
N0
"
ln )
=
ln
ln(1 + ξ)
!
En
E0
"
= ln
!
En
E0
ln !
" ln(1+ξ)
.
(1.26)
Resta ora da determinare la quantità ).
Attraverso la superficie dello shock entra, per unità di tempo e di area, (verso
la regione down-stream) un flusso di particelle J+ e ne esce un flusso J− , mentre
un flusso J∞ esce dalla zona down-stream all’infinito; dato che il tempo di vita
della regione accelerante sarà molto maggiore di un ciclo di accelerazione, si avrà
una situazione stazionaria per cui tante particelle entrano nella zona down-stream
e tante ne escono: J+ = J− + J∞ .
La probabilità di tornare allo shock è data da:
)=
J−
J−
=
;
J+
J− + J∞
(1.27)
vediamo quindi quanto vale J− , sapendo che il flusso di particelle che passano dalla
regione down-stream a quella up-stream, per unità di tempo e superficie, è nvx =
nc cos θ, con cos θ positivo (n è il numero di particelle nella zona post-shock).
Il numero totale di particelle che attraversa la superficie è:
/
dΩ
nc
J− =
nc cos θ = .
(1.28)
4π
4
cos θ≥0
12
Il numero di particelle che viene invece rimosso per unità di tempo e superficie è
dato da:
J∞ = nu2 ;
(1.29)
troviamo cosı̀:
)=
c
4u2
≈1−
.
c + 4u2
c
(1.30)
ln #
A questo punto, scrivendo, α = − ln(1+ξ)
, possiamo scrivere lo spettro in questo
modo:
! "−α
En
Nn = N0
,
(1.31)
E0
abbiamo cioè calcolato la distribuzione integrale, ovvero il numero di tutte le particelle che hanno compiuto n o più cicli.
La distribuzione differenziale sarà:
dN ∝ E −1−α dE.
(1.32)
Vediamo ora quanto vale l’esponente di E nel caso che ci interessa, e cioè quello
dell’accelerazione da shock; sostituendo le espressioni trovate per ξ e ) in α si ha:
%
&
ln 1 − 4uc 2
ln )
3u2
α=−
=−
,
(1.33)
4 u1 −u2 ≈
ln(1 + ξ)
u1 − u2
ln(1 + 3 c )
dunque sapendo che le velocità sono legate dal fattore di compressione r:
3
.
r−1
α=
(1.34)
L’indice spettrale sarà quindi determinato dal solo salto di velocità:
dN
∝ E −γ ,
dE
γ=
r+2
,
r−1
(1.35)
e nel caso di shock forte, per cui vale r = 4, si avrà γ = 2.
1.3.2
Energia massima
Finora non abbiamo considerato il fatto che la regione attorno allo shock ha
dimensioni finite, nè il fatto che la propagazione dello shock può durare un tempo
finito; se si tiene conto di questi fattori si trova che esiste un’energia massima oltre la
quale le particelle non possono essere accelerate. Calcoliamo innanzitutto il tempo
ta di accelerazione.
Analizziamo il problema in una dimensione, considerando prima di tutto il fatto
che nella regione up-stream la distribuzione delle particelle non è uniforme, e quindi
ci sarà un flusso diffusivo: −D1 dn/dx, dove D1 è un coefficiente di diffusione scalare;
13
si oppone alla diffusione il fenomeno della convezione, per cui il contributo del flusso
che riporta la particella verso lo shock sarà nu1 .
Il flusso totale di particelle attraverso la superficie dello shock sarà quindi:
J = −D1
dn
+ nu1 ,
dx
(1.36)
e tale flusso, in situazione stazionaria, si deve annullare. Per cui si trova, nella
regione up-stream:
u1 x
n(x) = n0 exp D1
(1.37)
dove n0 è la densità di particelle allo shock (x = 0).
Il numero totale N di particelle per unità di superficie è:
N=
/0
dx n(x) =
−∞
n0 D 1
;
u1
(1.38)
quindi sapendo che il numero di particelle (per unità di tempo e superficie) entranti
nella zona up-stream è J− = n40 c , si può trovare il tempo che la particella trascorre
proprio nella regione up-stream:
t1 =
N
4D1
=
.
J−
u1 c
(1.39)
Allo stesso modo si può calcolare il tempo trascorso nella zona down-stream: t2 =
4D2
e quindi la durata di un ciclo sarà:
u2 c
tcycle = t1 + t2 =
4D1 4D2
+
.
u1 c
u2 c
(1.40)
In questo intervallo di tempo l’energia della particella sarà aumentata di una quantità ∆E/E (calcolata precedentemente), e dunque si avrà:
∆E
4(u1 − u2 ) E
E
=
=
∆t
3c
tcycle
ta
(1.41)
dove il tempo di accelerazione ta è:
3
ta =
u1 − u2
!
D1 D2
+
u1
u2
"
.
(1.42)
Per quanto riguarda il coeffieciente di diffusione, si utilizza il coefficiente di diffusione
di Bohm:
1
D = λv,
(1.43)
3
14
dove λ è il libero cammino medio della particella sottoposta alla diffusione, e v la
sua velocità. Prendendo v ≈ c e λ uguale al raggio di Larmor della particella il
coefficiente diventa:
1 Ec
D=
(1.44)
3 ZeB
e quindi otteniamo
!
"
c
1
1
ta = αE, α ≡
+
,
(1.45)
Ze(u1 − u2 ) u1 B1 u2 B2
dove si vede che il tempo di accelerazione della particella è lineare nell’energia.
E’ importante precisare che il coefficiente di diffusione qui utilizzato riguarda le
turbolenze del campo magnetico su piccola scala (dell’ordine delle dimensioni dei
resti di supernovae, ∼ 1 pc).
Nel caso che stiamo considerando sarebbe più appropriato utilizzare una forma del coefficiente di diffusione che possa valere per scale più grandi in modo da
considerare le turbolenze del campo magnetico nel mezzo interstellare (per esempio
il coefficiente di diffusione alla Kraichnan vale per scale dell’ordine di ∼ 100 pc e
associa la turbolenza del campo magnetico alle fluttuazioni di densità prodotte dall’esplosione di supernovae nel mezzo interstellare).
Tuttavia, poichè come ordine di grandezza la diffusione alla Bohm dà la risposta
corretta, ci limitiamo all’utilizzo di tale coefficiente anche su scale maggiori di 1 pc.
Nel caso delle Supernovae, dove si hanno tipicamente shock forti (u2 = u1 /4),
ponendo D1 = D2 = D si trova che
!
"
4 E
1
1
20 E
tcycle =
+
=
(1.46)
3 ZeB u1 u2
3 ZeBu1
e calcolando infine Emax si trova:
Emax =
/ta
∆E
3 ZeB 2
dt =
u ta
∆t
20 c 1
(1.47)
0
dove il tempo di accelerazione sarà, in questo caso, uguale all’età del resto di supernova.
Il massimo di E si raggiunge all’inizio della fase di Sedov (di cui si parlerà nel
capitolo che segue), ovvero alla fine della fase di espansione libera, quando la massa di materiale interstellare spazzato è uguale a quella espulsa nell’esplosione della
supernova, cioè quando:
4
πρ(u1 ta )3 = Mej .
(1.48)
3
Per valori tipici, ρ = 1cm−3 , u1 = 5 × 108 cm/s e Mej = 10M% si trova ta = 103 anni
e quindi:
Emax ≤ Z × 3 × 1013 eV.
(1.49)
15
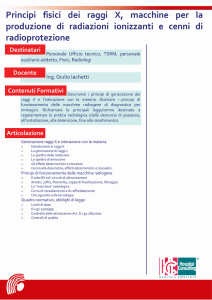
Figura 1.2:
Diagramma di Hillas.
Nel diagramma di Hillas (figura 1.2) sono state messe in relazione le dimensioni
e le intensità dei campi magnetici presenti in alcuni tipi di sorgenti astrofisiche; gli
oggetti al di sotto della corrispondente riga diagonale non possono accelerare rispettivamente protoni o nuclei di ferro a energie pari a 1020 eV.
Tale diagramma è un confronto tra le diverse sorgenti astrofisiche in base alla
relazione tra il raggio di Larmor rL della particella in esame e la dimensione della
regione accelerante; infatti se il raggio di Larmor della particella è molto maggiore
delle dimensioni tipiche della sorgente, la particella non si accorge del campo magnetico e il meccanismo ciclico descritto precedentemente non può avvenire.
Al contrario, se le dimensioni delle regioni up-stream l1 e down-stream l2 sono
molto maggiori del raggio di Larmor della particella il meccanismo risulta inefficiente
poichè la particella resta confinata in una delle due regioni.
La condizione ottimale per cui si verifichi l’accelerazione ciclica è che rL ≤ l1 , l2 .
16
Capitolo 2
Sorgenti di raggi cosmici
ultra-energetici
Lo spettro dei raggi cosmici riportato in figura 2.1 rappresenta la quantità
dN/dE, ovvero il numero di particelle per unità di superficie, di tempo e angolo
solido in funzione dell’energia misurata in GeV; si può osservare che tale spettro
esibisce un andamento a legge di potenza su un grande intervallo di energie, ma si
può anche vedere che esistono due diverse strutture, una intorno a 1015 eV (detta
ginocchio), e l’altra intorno a 1018 eV (detta caviglia).
Il fatto che lo spettro sia largamente esteso in energia e in flusso potrebbe far
pensare che siano coinvolti meccanismi di produzione e propagazione diversi tra loro,
mentre l’esistenza di due sole strutture (due cambiamenti di pendenza) indica che
esiste una certa universalità in questi meccanismi.
Nel capitolo precedente abbiamo trattato i meccanismi di accelerazione delle particelle in oggetti astrofisici, trovando un limite per l’energia massima raggiungibile:
Emax ∝ ZBLβ.
Analizzando le varie sorgenti astrofisiche conosciute si può vedere che l’energia
massima raggiungibile in sorgenti galattiche si trova intorno a energie corrispondenti
alla struttura della caviglia, dopo di che cominciano a dominare lo spettro i protoni
di provenienza extragalattica.
Nella prima parte di questo capitolo analizziamo quindi il meccanismo dell’accelerazione da shock nell’esplosione di Supernovae; per quanto riguarda invece l’accelerazione di raggi cosmici da parte di oggetti extragalattici, nella seconda parte
del capitolo si parla di nuclei galattici attivi come possibili candidati a sorgenti di
raggi cosmici ultra-energetici (UHECR).
2.1
Supernovae
Si possono distinguere alcuni tipi di Supernovae (come spiegato in [2], [3]); dal
punto di vista spettrale, le supernovae di tipo I non mostrano evidenza di righe di
17
Figura 2.1:
Spettro differenziale dei raggi cosmici.
emissione dell’idrogeno, diversamente dalle supernovae di tipo II.
Per quanto riguarda le Super Novae di tipo Ia, si pensa che l’esplosione abbia
origine in un sistema binario in cui una nana bianca sta gradualmente accrescendo
materia dalla compagna: quando la massa della materia in accrescimento porta la
massa totale della stella sopra la massa critica per una nana bianca (limite di Chandrasekhar ≈ 1.4M% ), inizia un processo di contrazione e riscaldamento che innesca
una rapida esplosione in cui vengono espulsi elementi pesanti per una massa totale
di 1.4M% .
Dal collasso del core di stelle più massive (probabilmente con masse > 8M% ) hanno invece origine Supernovae di tipo II e Ib; durante il collasso densità e temperature
diventano sufficientemente grandi da rendere possibile la reazione:
p + e− → n + νe ;
(2.1)
la quantità di energia rilasciata è 102 volte l’energia di una SN Ia, ma viene trasportata per lo più da neutrini; infatti solo l’1% di questa viene trasferito al materiale
esploso dalla stella, che viene spazzato via a velocità di circa 3 ÷ 4 × 104 kms−1 e che
costituisce la parte visibile della supernova.
Si pensa che SN di questo tipo provengano da stelle che attraversano uno stadio
intermedio come giganti rosse, durante il quale gli strati più esterni dell’atmosfera
possono essere spazzati via in un vento dalla velocità di circa 10ms−1 che precede la
fase esplosiva.
18
Se la massa iniziale supera 16 − 20M% , dopo lo stadio di supergigante rossa la
stella attraverserà lo stadio di Wolf Rayet, in cui un forte vento (circa 103 kms−1 )
spazzerà via gli strati più esterni (costituiti da idrogeno) per circa 105 anni precedenti
l’esplosione; il materiale rilasciato nell’esplosione sarà quindi costituito da elementi
più pesanti dell’idrogeno. Tale tipo di supernova è detto SN Ib.
Dal collasso del core di stelle ancora più massive hanno origine supernovae di
tipo Ic, un tipo molto più raro rispetto agli altri; per tutti i tipi di SN si ha un
rilascio simile di energia, pari a circa 1051 erg.
Il ritmo di esplosione di SN in una galassia è di circa 3 per secolo.
2.1.1
Esplosione di Supernovae
Consideriamo un’esplosione che conferisca ad una massa Mej un’energia cinetica E, e che questa esplosione avvenga entro un mezzo interstellare di densità ρ;
l’esplosione può essere divisa in tre fasi distinte:
• espansione libera
• fase adiabatica (o di Sedov)
• fase di spazzaneve
Inizialmente, finchè la massa totale del mezzo interstellare raccolta Ms è molto minore della massa eiettata, l’espansione procede liberamente, con velocità v data da
E ≈ Mej v 2 /2.
E’ a questo punto che si deve formare un’onda d’urto poichè, per tipici parametri
stellari, la velocità di espansione v ≈ 104 km/s è molto maggiore della velocità del
suono nel mezzo interstellare: per temperature tipiche, T ≈ 104 K, cs ≈ 10 km/s.
L’onda d’urto che si forma è seguita dal materiale che ha attraversato l’onda
d’urto stessa, e questo a sua volta è seguito dal materiale eiettato dalla SN. Queste
due componenti sono in equilibrio di pressione, ma la superficie che le separa rappresenta una discontinuità di contatto che è instabile. Ne segue che il materiale
passato attraverso lo shock e quello eiettato daranno origine a forti moti turbolenti
che li mischiano.
La fase di espansione libera cessa quando la massa di mezzo interstellare raccolta
diventa comparabile alla massa eiettata, e cioè quando:
!
"1/3
4
3Mej
3
πρRs = Ms = Mej ⇒ Rs =
(2.2)
3
4πρ
dove Rs è il valore del raggio dello shock quando si ha l’uguaglianza delle masse.
Quindi dopo un tempo T (tempo di Sedov) pari a:
!
"1/3 !
"−1/2
Rs
3Mej
2ESN
Ts =
=
v
4πρ
Mej
−1/2
= 0.439E51
5/6
−1/2
Mej ρ−1/3 = 186E51
19
5/6 −1/3
Mej% nH
,
(2.3)
lo shock comincerà a rallentare (sono stati indicati con E51 l’energia della materia
espulsa in unità di 1051 erg, con Mej% la massa espulsa in unità di massa solare e
con nH la densità in numero di particelle dell’ISM).
Assumendo Mej = 1.4M% , nH = 0.3cm−3 e E51 = 1 si avrà un tempo di Sedov
pari a ∼ 300 anni, ovvero all’incirca il tempo che ci separa dalla SN di tipo Ia
osservata da Tycho Brahe nel 1572.
Nella fase che segue quella dell’espansione libera si può idealizzare l’esplosione
della SN come quella di un mezzo che conservi l’energia totale, proprio per il fatto
che il gas che ha appena subito lo shock non riesce ad irradiare velocemente la sua
energia interna; la situazione è quindi descritta dalla soluzione di Sedov, per cui
valgono le seguenti relazioni:
Rs ∝ t2/5 ,
u1 ∝ t−3/5 ,
(2.4)
ovvero lo shock rallenta al passare del tempo.
Le shells più esterne della sfera in espansione decelerano prima, e quindi la densità di materia aumenta proprio al bordo della sfera stessa; durante la decelerazione,
quindi, si formerà un’onda d’urto che si propaga all’indietro nel materiale.
A questo punto la struttura della SNR è cosı̀ composta: la zona centrale è in
espansione libera, poi il reverse shock separa il materiale in espansione libera da
quello che già si muove secondo la soluzione di Sedov (e cioè sta rallentando), e,
infine, il materiale che deve ancora attraversare lo shock.
L’onda d’urto interna si propaga all’indietro attraverso il gas in espansione riscaldandolo; quindi mentre nella fase iniziale l’energia cinetica dell’espansione veniva
trasferita alla materia spazzata, nella fase di decelerazione l’energia cinetica viene
anche trasmessa al gas espulso. Tutto questo risulta nell’emissione X che si osserva
da molte SNR.
Quando la perdita di energia per radiazione diventa importante, l’espansione
della SNR non può più seguire la soluzione di Sedov, ma procede emettendo in varie
righe; per bilanciare la diminuzione della temperatura del gas si avrà quindi una
compressione della materia in uno strato immediatamente dopo lo shock (fase dello
spazzaneve).
Successivamente la veocità dell’espansione diventerà subsonica e la SNR perde
la sua identità.
2.1.2
Accelerazione in Supernovae
Riguardo al caso dell’accelerazione di raggi cosmici, applichiamo il meccanismo
di accelerazione da shock descritto nel capitolo 1 alla fase di Sedov dell’esplosione
di supernova; per capire quale energia massima possono raggiungere le particelle
accelerate nelle onde d’urto dobbiamo confrontare il tempo di diffusione (riportato
in appendice A) delle particelle con il tempo di vita della regione accelerante, impondendo che il tempo di diffusione sia minore.
20
Nel caso dell’accelerazione in resti di supernovae si può utilizzare il coefficiente
di diffusione alla Bohm che ha validità locale:
1
DB = λrL = 1022 Bµ−1 EGeV cm2 /s = D0 EGeV
3
(2.5)
! = 3µG)
dove Bµ è la componente regolare del campo magnetico galattico (|B|
ottenendo un limite per l’energia massima:
Emax =
u2 T
GeV.
D0
(2.6)
Il tempo T da sostituire nell’equazione sopra è proprio il tempo di Sedov Ts cioè il
tempo dopo cui la velocità dell’onda d’uto comincia a diminuire.
Avendo tempi di vita dei resti di supernovae dell’ordine di 103 anni e velocità
tipiche dell’espansione pari a 104 km/s si può vedere che l’energia massima raggiungibile in questi siti di accelerazione è di circa 1015 eV per i protoni; per i nuclei più
pesanti l’energia massima sarà più alta, in quanto DB ∝ 1/Z e quindi Emax ∝ Z:
nel caso di nuclei di Ferro si possono raggiungere energie di 1017 eV.
Oltre queste energie cominciano a dominare lo spettro i protoni extragalattici.
2.2
Nuclei galattici attivi
I nuclei galattici attivi (AGN) sono da lungo tempo considerati possibili siti per
la produzione di particelle energetiche, dove protoni e nuclei potrebbero essere accelerati fino alle più alte energie misurate.
In questa sezione si riportano le caratteristiche degli AGN, iniziando dalle loro
classificazioni ([5]), e si descrivono le teorie che applicano il meccanismo dell’accelerazione da shock ai jets presenti in questi oggetti.
Pur avendo nomi e caratteristiche spettrali diverse, i nuclei galattici attivi, come
evidenziato dalla teoria di unificazione degli AGN (sezione 2.2.1), sono galassie con
al centro un buco nero supermassivo; le classificazioni, come verrà specificato meglio
in seguito, sono basate sull’orientazione dell’AGN rispetto alla linea di vista.
Galassie di tipo Seyfert
La definizione originaria della classe (Seyfert, 1943) era basata su considerazioni
morfologiche; attualmente l’identificazione di galassie di questo tipo avviene grazie
all’identificazione della presenza di forti righe di emissione.
Le Seyfert sono state poi divise in due sottoclassi (Khachikian & Weedman,
1974). Nello spettro delle galassie di tipo Seyfert 1 (Sy1) è presente una forte emissione continua dall’infrarosso all’X, mentre per quanto riguarda le righe di emissione,
se ne osservano due set sovrapposti: uno di questi è caratteristico di un gas ionizzato
21
Figura 2.2:
Spettro ottico della galassia Seyfert 1 NGC 1275.
a bassa densità e le righe si identificano come righe ‘strette’; l’altro set è costituito
invece da righe di emissione più larghe.
Le galassie di tipo Sy2 differiscono dalle prime perchè nello spettro la componente continua è più debole e sono presenti solo righe strette.
Successivamente Osterbrock (1981) ha diviso le Sy1 in cinque sottoguppi, sulla
base della presenza o meno di righe di Balmer: Sy1.0, 1.2, 1.5, 1.8, 1.9.
Le Sy1.0 sono i membri tipici della classe, mentre per esempio le Sy1.5 sono considerate oggetti intermedi tra le tipiche Sy1 e Sy2, poichè l’intensità delle componenti larghe è confrontabile con quella delle righe strette nel profilo Hβ. I sottogruppi
Sy1.2 e 1.8 sono utilizzati per descrivere oggetti con righe Hβ rispettivamente più
deboli o più forti, che quindi nella classificazione sono intermedi tra Sy1.0 e 1.5,
Sy1.5 e 2, rispettivamente. Nelle Sy1.9 la componente larga è visibile solo nella riga
Hα e non nelle righe di Balmer di ordine più alto.
Nella 12a edizione del catalogo di nuclei attivi e quasars ([6]) di Veron-Cetty &
Veron (VCV) da noi utilizzato è stato adottata la classificazione introdotta da Winkler (1992), che si basa sul rapporto R tra l’intensità delle righe Hβ e [OIII]λ5007:
• Sy1.0 5.0<R
• Sy1.2 2.0<R<5.0
• Sy1.5 0.33<R<2.0
• Sy1.8 R<0.33 righe larghe visibili nei profili Hα e Hβ
22
• Sy1.9 righe larghe visibili in Hα ma non in Hβ
• Sy2 righe larghe non visibili
Quasars
I Quasar (Quasi Stellar Radio Source) comprendono la sottoclasse più luminosa
degli AGN, con magnitudini assolute M < −23; si distinguono dalle Seyfert per il
fatto che non si risolvono spazialmente, e gli spettri evidenziano delle righe strette
più deboli che nelle Seyfert.
BL Lac e OVV
Esiste un piccolo sottogruppo di AGN che mostra rapide e ampie variazioni nel
flusso (per esempio variazioni di magnitudine ∆m ≈ 0.1 su tempi scala di un giorno);
questi oggetti vengono classificati come OVV (Optically Violent Variables).
Alcune delle proprietà delle OVV vengono condivise con le BL Lac, chiamate
cosı̀ dal nome di quello che si considera il prototipo di questa classe, BL Lacertae,
che era stato originariamente identificato come una stella variabile. Le BL Lac si
distinguono dalle OVV per l’assenza di forti righe di emissione o assorbimento.
Si pensa che entrambi questi tipi di oggetti siano AGN con una componente
relativistica direzionata vicino alla linea di vista; ci si riferisce a questi oggetti anche
con il nome di blazar. Tutti i blazar noti sono anche sorgenti radio.
Radio Galassie
La classificazione degli AGN può essere rivista anche considerando un altro importante tipo di emissione: l’emissione Radio. Studiando la morfologia delle osservazioni nel radio, sono state fatte delle classificazioni (Fanaroff & Riley) misurando
il rapporto R tra la distanza tra i due punti più luminosi e le dimensioni totali dell’immagine radio.
In questa classificazione si dividono quindi le galassie in cui dominano le emissioni
radio di lobi uscenti dal nucleo (FR II) da quelle in cui sono presenti dei getti luminosi più stretti (FR I).
Analizzando gli spettri ottici di queste galassie, vengono ridenominate BLRG
(radio galassie con righe di emissione larghe) e NLRG (radio galassie con righe di
emissione strette), ovvero la controparte radio delle galassie Seyfert di tipo 1 e 2
rispettivamente.
LINERs
Si può avere una ulteriore classificazione a parte per una classe di galassie con regioni a bassa ionizzazione (Low-Ionization Nuclear Emission-line Region); dal punto
di vista spettroscopico, anche questi oggetti possono rientrare nella classificazione
23
Figura 2.3:
Immagine radio della galassia attiva Cygnus A, classificata come FR II.
Spettro ottico della galassia Seyfert 2 NGC 1358 a confronto con spettri di altri
nuclei galattici attivi.
Figura 2.4:
delle Sy2, ma la particolarità che le accomuna consiste nell’intensità di alcune righe
([O I] e [N II]).
Markarian Galaxies
In letteratura è possibile trovare oggetti classificati come galassie di tipo Markarian, da una raccolta di osservazioni fatte per identificare oggetti con un eccesso di
emissione nell’UV. E’ stato successivamente stimato che circa l’11% di queste galassie
nel catalogo Markarian sono Seyfert, il 2% sono Quasar e BL Lac e le rimanenti sono
galassie normali.
24
Figura 2.5:
2.2.1
Sezione di un AGN con rappresentazione dell’emissione UV e X.
Unificazione degli AGN
La teoria di unificazione degli AGN ([7]) si basa sul fatto che le proprietà osservate negli spettri, e quindi la classificazione che ne deriva, dipendono dall’orientazione dell’oggetto rispetto all’osservatore. In particolare, nel caso delle Seyfert,
la differenza nella classificazione sarebbe dovuta al fatto che la linea di vista nella
direzione del buco nero centrale intercetti o meno una struttura di forma toroidale
composta di gas e polveri, che assorbirebbe la radiazione X emessa dal disco della
galassia.
Inoltre alcuni AGN emettono fortemente nel radio, e le immagini di questi oggetti in tali lunghezze d’onda mostrano dei jets molto luminosi; la classificazione dei BL
Lac come oggetti fortemente variabili dovrebbe quindi dipendere proprio dal fatto
che la linea di vista intercetta il jet relativistico dell’AGN.
Secondo la teoria di unificazione degli AGN, al centro di tali oggetti si dovrebbe
trovare un buco nero di 106 ÷ 1010 M% , circondato da un disco di accrescimento.
Questa struttura è formata da gas e polveri della galassia che si trovano nella
regione del buco nero; la materia in caduta assume un’orbita circolare attorno ad
esso. A questo punto entrano in gioco le forze viscose che redistribuiscono il momento angolare facendo sı̀ che la materia più vicina al buco nero centrale diminuisca
il momento angolare in modo da cadere nel buco nero.
L’emissione che si osserva provenire dal disco è dovuta proprio alla materia in
caduta; infatti mentre metà dell’energia potenziale si trasforma in energia termica
e il gas viene riscaldato, l’altra metà viene irradiata. Si deve inoltre tenere conto
dell’energia dissipata nel disco dalle forze viscose.
L’emissione risultante si avrà nella regione dello spettro corrispondente alle
lunghezze d’onda dell’ottico e dell’UV; si osservano inoltre emissioni nella banda
X, che si pensa siano dovute all’interazione dei fotoni UV dal disco con elettroni più
energetici presenti nella materia circostante attraverso il Compton inverso.
I fotoni X uscenti dallo scattering Compton vengono emessi in maniera isotropa;
una parte di questi fotoni arriverà dunque all’osservatore costituendo la parte con-
25
Figura 2.6:
Rappresentazione schematica della teoria di unificazione degli AGN
tinua dello spettro X.
I fotoni che investono nuovamente il disco potranno subire diversi processi, tra
cui l’assorbimento fotoelettrico se hanno energie < 10 keV, un nuovo scattering
Compton, oppure possono essere assorbiti e successivamente emettere grazie al processo della fluorescenza.
La riga Kα del Fe a 6.4 keV è la più forte di queste righe di emissione; studiando il profilo di questa riga è possibile avere informazioni sulla geometria e su altre
proprietà del disco di accrescimento nelle zone più interne vicine al buco nero.
Sono presenti inoltre delle nubi di materia, sedi dell’emissione di righe ‘larghe’ o
‘strette’ (Broad Line Regions, Narrow Line Regions).
La struttura toroidale descritta sopra potrebbe quindi nascondere, da alcune
direzioni, le Broad Line Regions, per cui lo spettro che risulta dalle osservazioni
possiede solo righe ‘strette’ e l’oggetto viene classificato come Sy2. Se invece l’asse
di rotazione dell’AGN è in linea con il punto di osservazione, la regione del toro non
oscurerà le Broad Line Regions, quindi l’oggetto viene classificato come Sy1.
I jets che si osservano in alcuni AGN sono probabilmente associati a shock
26
relativistici che, come discusso precedentemente, si possono considerare sede di
accelerazione di raggi cosmici.
2.2.2
Accelerazione in AGN
L’ipotesi dei nuclei galattici attivi come sorgenti di raggi cosmici è sostenuta dal
fatto che in questi oggetti è disponibile un enorme quantitativo di energia grazie
all’accrescimento della materia attorno al buco nero centrale.
Al momento attuale non esiste peò una conoscenza approfondita degli AGN dal
punto di vista dell’accelerazione. Sono stati infatti proposti diversi meccanismi che
utilizzano diverse regioni e proprietà di questi oggetti per accelerare raggi cosmici;
in questa sezione analizzeremo alcune delle teorie attuali, ma come si potrà vedere i
procedimenti utilizzati per stimare il parametro che ci interesserà in seguito, ovvero
l’energia massima di accelerazione dei raggi cosmici in questi siti, sono molteplici e
non si può definire con certezza un valore univoco per l’energia massima. Discuteremo il meccanismo dell’accelerazione da shock nei getti delle galassie radio e un
meccanismo alternativo all’accelerazione da shock basato sul campo elettrico ([14]).
In particolare, nell’ambito dell’accelerazione da shock sono state proposte diverse
regioni dell’AGN in cui può avvenire il meccanismo; nel seguente paragrafo si analizza il caso dell’accelerazione in hot spots, ovvero nelle zone finali dei radio lobi di
alcune galassie radio ([12]).
Si parla inoltre della radio galassia denominata Centaurus A, dove l’accelerazione
potrebbe avvvenire proprio nei radio lobi; in questo caso è possibile fornire un valore
per l’energia massima dei protoni iniettati nello spazio intergalattico ([13]).
Accelerazione in hot spots
Gli hot spots nelle radio galassie fortemente estese (galassie FR II) sono identificati come le parti finali dei getti espulsi dai nuclei delle galassie stesse nel mezzo
extragalattico; lo spettro di emissione radio può essere spiegato come radiazione di
sincrotrone da particelle accelerate in shock forti tramite il meccanismo dell’accelerazione di Fermi al I ordine.
La restrizione alla classe delle FR II come acceleratori di raggi cosmici è dovuta
al fatto che particelle cariche altamente energetiche prodotte all’interno di strutture
galattiche risentiranno di sostanziali perdite adiabatiche di energia nel loro moto
verso il mezzo extragalattico; questo problema si può applicare a molte possibili
sorgenti di raggi cosmici ma non alle macchie calde delle FR II, dal momento che
queste sono posizionate sulla zona finale dei radio lobi estesi e le particelle possono
facilmente passare nel mezzo extragalattico.
Protoni e altri nuclei più pesanti possono essere accelerati in onde d’urto; questi
nuclei energetici hanno perdite di energia abbastanza basse e si possono quindi
considerare i primi messaggeri della transizione in arrivo nella zona upstream.
27
Spettro dell’emissione di sincrotrone; x = ω/ωc , con ωc frequenza di cut-off
dell’emissione.
Figura 2.7:
Il moto relativistico del jet comporta la formazione di un’onda di shock in zone
in cui un ostacolo o una perturbazione del flusso crea un improvviso salto di velocità.
Lo shock più forte è solitamente quello che si forma proprio alla superficie finale del
jet.
Analizziamo quindi la produzione di particelle di alta energia nelle superfici finali
di getti in oggetti extragalattici; in generale, quando si ha uno shock, il meccanismo
di accelerazione che ha luogo è l’accelerazione di Fermi al primo ordine.
Sia per gli elettroni che per i protoni il tempo in cui una particella diffonde, cioè
la durata di un ciclo del meccanismo di accelerazione, si può definire come:
tdif f = ζ
D
u2jet
(2.7)
dove ujet è la velocità del getto e ζ = 3(r2 + r)/(r − 1) (r è il fattore di compressione
dello shock).
Scriviamo il coefficiente di diffusione D nella forma generale, come riportato in
Appendice A:
! "2−α
1
rL
D = lc v
(2.8)
3
lc
dove lc è la scala massima della turbolenza del campo magnetico, rL il raggio di
Larmor della particella e v la sua velocità; con α è indicato invece l’indice spettrale
dello spettro di turbolenza (α = 5/3 per la teoria di Kolmogorov e 3/2 per quella di
Kraichnan).
E’ utile in questo caso inserire nel coefficiente di diffusione un contributo che
tenga conto della forza della turbolenza; scriviamo ηT in questo modo:
ηT =
,δB 2 ,
B02 + ,δB 2 -
28
(2.9)
dove B0 e δB sono rispettivamente la parte imperturbata e la parte turbolenta del
campo magnetico. Si avrà che 0 ≤ ηT ≤ 1 e il coefficiente di diffusione per shock
paralleli (cioè il campo magnetico è parallelo alla normale allo shock) si può scrivere
quindi:
! "2−α
1 lc c r L
D=
,
(2.10)
3 ηT lc
dove abbiamo già preso la velocità della particella v ≈ c.
Le osservazioni radio forniscono, come detto precedentemente, uno spettro che
suggerisce che la radiazione è dovuta all’emissione di sincrotrone di particelle accelerate; il meccanismo di emissione da parte degli elettroni risulta essere più efficiente
rispetto all’emissione di sincrotrone da protoni in quanto la potenza di emissione è
P ∝ m−2 .
Lo spettro radio che si osserva si riferisce quindi all’emissione da parte di elettroni; cerchiamo quindi di capire quale possa essere l’energia massima a cui possono
essere accelerati gli elettroni nell’onda d’urto considerando le perdite di energia
dovute all’emissione, per trarre informazioni utili sull’energia massima raggiungibile
dai raggi cosmici.
Confrontando il tempo scala dell’accelerazione di Fermi al I ordine con il tempo
scala di sincrotrone si può calcolare l’energia massima alla quale vengono accelerati
gli elettroni nello shock finale del jet.
Imponiamo quindi che il tempo scala dell’emissione di sincrotrone dato da:
#v $
E
4
tsync =
, Psync = σT c
γ 2 )B ,
(2.11)
Psync
3
c
dove )B è la densità di energia del campo magnetico e σT la sezione d’urto Thomson
per l’elettrone, superi la durata di un ciclo di accelerazione. Otteneniamo:
4
)e,max = 9.6 × 10
!
2
ηT βjet
ζ
"3/4 !
B
0.1mG
"−5/4 !
lc
1kpc
"−1/2
GeV
(2.12)
dove βjet = ujet /c. Nei calcoli qui riportati si utilizza il valore α = 5/3 (Kolmogorov),
in quanto in questo caso D ∝ E 1/3 .
In corrispondenza dell’energia massima dell’elettrone sappiamo che lo spettro
di sincrotrone mostra un massimo dopo il quale lo spettro viene esponenzialmente
tagliato; la frequenza corrispondente al cut-off sarà:
hνc = 16.8
!
2
ηT βjet
ζ
"3/2 !
B
0.1mG
"−3/2 !
lc
1kpc
"−1
keV
(2.13)
che corrisponde ai fotoni a più alta energia prodotti dagli elettroni relativistici attraverso il meccanismo di sincrotrone.
29
Il cut-off dello spettro dipende in questo modello da quantità che riguardano la
hot spot; immaginando il caso di shock forte (ζ = 20) con velocità del jet pari a
0.2÷0.5c e con la scala massima di turbolenza lc comparabile con le dimensioni della
hot spot (10−1 ÷ 1kpc), si ottengono valori del cut-off di sincrotrone pari a 1 ÷ 100
eV ×(ηT /B0.1 )3/2 .
Da questo risultato si vede quindi che il livello di turbolenza e il campo magnetico sono i parametri più importanti per delimitare l’energia di cut-off del sincrotrone;
da notare che minore è il campo magnetico, maggiore sarà l’energia di cut-off.
L’informazione fornita dallo spettro degli elettroni deve essere ora utilizzata per
stimare l’energia massima dei protoni accelerati nelle stesse onde d’urto; contrariamente agli elettroni il meccanismo principale di perdita di energia è la fuga delle
particelle dalla macchia calda.
In generale, il tempo di fuga di una particella da una regione asimmetrica è dato
da:
! 2 "
Lk
tesc = mink
(2.14)
4Dk
dove l’indice k sta per le dimensioni dell’oggetto nelle varie direzioni. Considerando
le hot spots, prendiamo le stesse dimensioni LHS in ogni direzione e quindi: tesc =
mink (L2HS /4Dk ); eguagliando i tempi scala dell’accelerazione di Fermi al I ordine e
quello di fuga dalla regione accelerante si trova l’energia massima che i raggi cosmici
possono raggiungere:
)CR,max
= 1.53
Z1021 eV
!
2
ηT βjet
ζ 1/2
"3 !
B
0.1mG
"!
lc
1kpc
"!
LHS
lc
"3
(2.15)
Da questa espressione si vede che anche in questo caso l’energia massima raggiungibile può essere scritta in termini di quantità che riguardano le caratteristiche della
hot spots, cosı̀ come è stato fatto per l’energia massima degli elettroni e per la frequenza di cut-off.
Essendo nota quindi la frequenza di cut-off dell’emissione di sincrotrone degli
elettroni, il valore dell’energia massima dei raggi cosmici si può riscrivere:
!
"2 ! 3/2 " !
"4 !
"3
)CR,max
hνc
ζ
B
LHS
= 1.53
(2.16)
3
Z1021 eV
16.8keV
βjet
0.1mG
1kpc
In questo modo le relazioni trovate sono indipendenti dalle caratteristiche locali
della turbolenza (ηT o lc ); la misura dell’intensità del campo magnetico è molto
importante poichè, insieme al cut-off osservato del sincrotrone dà una stima diretta
dell’energia massima raggiungibile, sempre che si abbia un’idea della velocità del jet.
La conclusione principale è che i migliori candidati per l’accelerazione di raggi
cosmici sono galassie radio con hot spots estese (LHS ≥ 1 kpc) in cui siano presenti
campi magnetici molto alti (B ≥ 0.1 mG); l’energia di cut-off per l’emissione di
sincrotrone deve essere almeno nella banda ottica.
30
Il caso migliore è quello della galassia radio 3C 273 A, una galassia a redshift z =
0.158, che mostra un’energia di cut-off pari a 1.74 eV e valori osservativi di campo
magnetico e velocità del getto pari rispettivamente a 0.35 mG e 0.27c; prendendo
inoltre ζ = 20 e LHS = 1.9 kpc si ottiene )CR,max ∼ 7 × 1019 eV.
In questa teoria la radiazione di sincrotrone emessa dagli elettroni relativistici è
la principale fonte di informazioni che abbiamo sulle particelle relativistiche nei jets;
la luminosità totale proveniente dall’emissione di sincrotrone ci permette di avere
delle stime sulla densità di energia trasportata da protoni e elettroni e dal campo
magnetico.
In ogni caso l’incognita che rimane è l’efficienza della conversione della potenza
del jet in densità di energia di nuclei relativistici.
L’applicazione del ‘classico’ meccanismo di accelerazione da shock alla produzione
di particelle UHE nei jets extragalattici incontra però alcune difficoltà; a causa delle
ridotte dimensioni spaziali della hot spot, la fuga delle particelle dovuta alla diffusione può costituire un limite per il raggiungimento di energie oltre 1020 eV.
Inoltre la presenza di eventuali campi magnetici obliqui rispetto alla normale allo
shock potrebbero contribuire all’aumento del numero di particelle che fuoriescono
dalla regione accelerante causando dei moti di deriva lungo la superficie dello shock.
E’ stato osservato che anche una discontinuità tangenziale del campo di velocità
può costituire un efficiente sito si accelerazione di raggi cosmici se la differenza tra
le velocità è relativistica e è presente una turbolenza su entrambi i fronti [11].
Centaurus A
Centaurus A è una sorgente radio estremamente potente identificata nella banda
ottica con la galassia NGC 5128; è la galassia radio più vicina (3.5 Mpc). Osservazioni radio in diverse lunghezze d’onda mostrano una struttura composta da un
core compatto, un jet e alcuni lobi esterni e interni; questa morfologia suggerisce la
classificazione di questo oggetto come galassia radio attiva con un jet che forma un
piccolo angolo con la linea di vista.
Il jet è responsabile della formazione dei lobi radio denominati Northern Middle
Lobe e Northern Inner Lobe interagendo rispettivamente con il mezzo intergalattico
e con quello interstellare; in particolare il Northern Middle Lobe può essere considerato come la zona in cui vengono prodotti forti shocks dalle collisioni del plasma,
cioè si può vedere come una ‘macchia’ più calda della galassia.
L’accelerazione di particelle nella ‘macchia’ è il risultato dei ripetuti scatterings
avanti e indietro attraverso il fronte dello shock in un campo magnetico turbolento.
Il processo di accelerazione sarà efficiente finchè non diventano dominanti le
perdite di energia per emissione di sincrotrone e per interazioni pγ.
31
Il tempo scala dell’accelerazione può essere scritto in questo modo [13]:
!
"−1
dEp
40 −2 2/3 Ep
Ep
≈ βjet
uLHS
,
dt ACC
πc
eB
(2.17)
dove βjet è la velocità del getto, u è il rapporto tra la densità di energia del campo
magnetico turbolento e la densità del campo magnetico regolare nella hot spot (di
raggio LHS ) e B è l’intensità del campo magnetico totale.
I protoni più energetici iniettati nel mezzo intergalattico avranno un’energia che
si può stimare bilanciando le perdite di energia e i guadagni; il tempo scala delle
perdite di energia per interazioni pγ si stima essere:
!
"−1
6πm4p c3
dEp
Ep
≈
E −1 ,
(2.18)
dt LOSS
σT m2e B 2 (1 + aA) p
dove a sta per il rapporto tra la densità di energia in fotoni e la densità di energia del
campo magnetico, σT è la sezione d’urto Thomson e A dà la misura dell’importanza
delle interazioni pγ rispetto all’emissione di sincrotrone (è stato stimato A ∼ 200).
Si trova quindi
! "3/4
m2p −1/2 −5/4
u
3
1/4 3/2
Ep,max = 10 c e βjet
LHS B
(1 + aA)−3/4 MeV.
(2.19)
3/2
σT
me
Nel caso di Cen A si può stimare u dall’indice spettrale dell’emissione di sincrotrone nel Northern Middle Lobe e si ottiene u ≈ 0.4; è possibile inoltre misurare
direttamente le dimensioni della hot spot dalla mappa radio della galassia trovando
LHS ∼ 1.75 kpc.
Il campo magnetico totale B è dell’ordine di 50µG, mentre per βjet si assume 0.3,
valore tipico trovato per altre sorgenti simili; con questi valori l’energia massima dei
protoni iniettati nello spazio intergalattico è di circa 2.7 × 1021 eV.
Per questa sorgente è stato inoltre possibile dedurre l’indice della legge di potenza dello spettro dalle osservazioni alle varie lunghezze d’onda dela radiazione di
sincrotrone prodotta dalla componente leptonica delle particelle accelerate (p = 2.2).
Accelerazione induttiva
Il processo di diffusione finora considerato per l’accelerazione di raggi cosmici
consiste nella diffusione della particella non termica a causa del campo magnetico;
ipotesi alternative per l’accelerazione di UHECR nei jets di galassie attive prendono
invece in considerazione il campo elettrico iduttivo.
Il modello qui riassunto presenta alcune similitudini con la teoria dell’accelerazione da shock in onde d’urto non parallele; se infatti il campo magnetico non
è esattamente parallelo alla direzione di moto dello shock può esistere un campo
elettrico parallelo alla superficie. Non è detto, però, che l’origine del campo elettrico
32
sia sempre dovuta alla presenza di un’onda d’urto.
In ambito astrofisico, ci aspettiamo comunque che i campi elettrici non contino
più dei campi magnetici. In questo contesto il rate di accelerazione più alto possibile
è dato dall’inverso della frequenza di Larmor, ∼ γ/ZωB , dove Z è la carica della
particella e ωB = eB/mc.
Se si parametrizza il campo elettrico E in modo che E = β0 B e se la regione accelerante ha dimensioni tipiche R, il potenziale disponibile è dato da Φ ∼ RE ∼ β0 RB
e l’energia di una particella che attraversi questo potenziale:
E = Zeβ0 BR.
(2.20)
Il fatto che β0 ∼ 1 implica che il raggio di Larmor della particella sia minore di
R; quindi in questo caso il sistema sarebbe in grado di accelerare particelle fino
all’energia massima con cui può confinarle. Essendo BR una misura della corrente
totale nel sistema, l’equazione sopra può essere riscritta in questo modo (assumendo
β0 ∼ 1):
2I
Φ = β0 ;
(2.21)
c
questo determina il potenziale elettrico massimo e la corrispondente energia E =
ZeΦ alla quale un sistema che trasporti una corrente I può accelerare delle particelle.
Analizziamo il flusso di Poynting nel sistema; poichè la luminosità di Poynting
non può essere maggiore della luminosità totale di una data sorgente, e assumendo
un’espansione sferica troviamo:
L = 4πR2
1 + α EB
1+α 2 2
1+α 1 2
c∼
R B β0 c =
φ c,
α 4π
α
α β0
(2.22)
dove α è il rapporto tra il flusso di Poynting e il flusso di particelle.
A questo punto, assumendo β0 ∼ 1,
L=
1+α
IΦ.
α
(2.23)
L’equazione sopra mette in relazione il potenziale massimo disponibile alla luminosità della sorgente; assumendo che gli UHECR siano protoni, si possono selezionare possibili candidati per l’accelerazione di UHECR in base alla loro luminosità: per raggiungere 3 × 1020 eV sono necessarie luminosità L ≥ 1046 erg/s.
Da qui si può ipotizzare che possibili sorgenti di UHECR siano rappresentate da
radio-galassie di tipo FR I e FR II, quasars che emettono nel radio e Gamma Ray
Bursts.
Un’altra richiesta che il sito di accelerazione deve soddisfare è che le perdite radiative della particella non dovrebbero degradare l’energia della stessa; si possono
derivare dei limiti sulla possibile collocazione dell’accelerazione di raggi cosmici dal
33
bilanciamento dell’accelerazione più efficiente (E ∼ B) e delle perdite radiative.
Confrontando il tasso massimo di guadagno di energia con le perdite radiative
si può quindi ottenere una seconda richiesta sul sito di accelerazione di particelle; si
trovano infatti dei valori limite per il campo magnetico e le dimensioni della regione
accelerante.
Da qui si trova che i raggi cosmici a energie più alte vengono accelerati meglio a
grandi distanze; i jets degli AGN, che si propagano per distanze di più di 100 kpc,
sono quindi da considerarsi possibili siti di accelerazione.
Inoltre ha che finchè il jet rimane relativistico, il potenziale induttivo è approssimativamente conservato, quindi la particella può essere accelerata anche dopo un
certo tempo, senza che la sua energia sia sostanzialmente dissipata.
Dunque gli UHECR possono essere accelerati all’interno del jet a distanze di
frazioni di parsec fino a centinaia di kpc, finchè il jet rimane relativistico e possiede
un grande potenziale induttivo.
34
Capitolo 3
Propagazione di raggi cosmici
In questo capitolo si analizza la propagazione dei raggi cosmici dalla sorgente
fino alla rivelazione; si parla inizialmente delle varie perdite di energia che subiscono
i protoni, per poi spiegare come queste contribuiscano a determinare la forma dello
spettro in energia, insieme all’iniezione.
Si riportano inoltre i procedimenti per il calcolo del flusso da una singola sorgente e da una distribuzione di sorgenti, considerando il contributo dell’espansione
dell’universo sull’espressione del flusso.
Queste formule verranno poi richiamate nell’ultimo capitolo per il calcolo del
flusso da un insieme di sorgenti discrete (come somma di flussi da singole sorgenti)
e da una distribuzione omogenea di sorgenti.
3.1
Perdite di energia
La perdita di energia da parte di protoni energie oltre 1018 eV è dominata dai
seguenti processi:
• Perdita adiabatica di energia per espansione dell’universo;
• Interazione con la radiazione cosmica di fondo (CMBR).
Nel caso della perdita adiabatica di energia si avrà:
−
1 dE
= H0
E dt
(3.1)
con H0 = 7.7 × 10−11 y−1 .
Le perdite di energia continue di protoni UHE per unità di tempo dovute alle
interazioni con fotoni a bassa energia sono date da ([17]):
1 dE
c
−
= 2
E dt
2Γ
/∞
d)r σ()r )f ()r ))r
#th
/∞
#r /2Γ
35
d)
nγ ())
,
)2
(3.2)
Perdite di energia dei protoni
-7
pair production e π production
perdite adiabatiche
log[β (y-1)]
-8
-9
-10
-11
-12
17
17.5
18
18.5
19
19.5
log[E (eV)]
20
20.5
21
Perdite di energia dei protoni a z = 0; la linea tratteggiata rappresenta le
perdite adiabatiche.
Figura 3.1:
dove Γ è il fattore di Lorentz del protone di energia E, )r l’energia del fotone di
fondo nel sistema di riferimento in cui il protone è a riposo, )th la soglia della
reazione considerata (sempre nel riferimento in cui il protone è a riposo), σ()r ) la
sezione d’urto, f ()r ) la frazione media di energia persa dal protone in una collisione
pγ nel sistema del laboratorio e nγ ()) la densità dei fotoni di fondo.
Tale relazione, usando la n()) dei fotoni della CMBR (che hanno temperatura
T)
1
)2
n()) = 2
(3.3)
π (!c)3 exp()/kT ) − 1
diventa:
1 dE
ckT
−
= 2 2
E dt
2π Γ (!c)3
/∞
#th
0
# ) $.1
r
d)r σ()r )f ()r ))r − ln 1 − exp −
.
2ΓT
(3.4)
L’interazione con la CMBR comporterà delle perdite di energia dovute a creazione
di coppie:
p + γCM BR → p + e+ e−
(3.5)
o a fotoproduzione di π:
p + γCM BR → N + π
(3.6)
Analizziamo le energie di soglia dei due processi; nel caso della produzione di coppia
si ha:
(Ep + Eγ )2 − (!pp + p!γ )2 = (mp + 2me )2
(3.7)
36
ovvero
(mp + 2me )2 − m2p
Ep =
2Eγ (1 − cos θ)
(3.8)
L’energia minima del protone per avere produzione di coppia si avrà nel caso in cui
θ = π, per cui
Epth (Eγ = kT, θ = π) =
me
me m p
(me + mp ) ≈
≈ 2.5 × 1018 eV.
kT
kT
(3.9)
e mp
A energie E . mkT
(ovvero quando la reazione avviene con i fotoni della CMBR
che hanno energie più alte, ) / kT ), la frazione di energia persa da un protone in
una collisione e la sezione d’urto sono determinati dai valori di soglia:
!
"3
2me
π 2 )r
fth ≈
, σth ≈ αr0
−2 .
(3.10)
mp
12
me
Si può quindi calcolare la perdita di energia:
!
"
! "3 !
"2
2
1 dE
kT
ΓkT
16c me
ec
2
−m
ΓkT ,
−
αr0
e
=
E dt p e+ e−
π mp
!c
me c 2
(3.11)
1
dove α = 137
e r0 il raggio classico dell’elettrone.
A energie più alte comincia a contribuire la reazione di fotoproduzione di π;
analizziamo anche in questo caso l’energia di soglia del processo:
(Ep + Eγ )2 − (!pp + p!γ )2 = (mN + mπ )2
(3.12)
(mN + mπ )2 − m2p
Ep =
.
2Eγ (1 − cos θ)
(3.13)
ovvero
Prendendo di nuovo θ = π, Eγ = kT e mN = mp si trova l’energia di soglia:
Epth (Eγ
2mp mπ + m2π
= kT, θ = π) =
≈ 7 × 1019 eV.
4kT
(3.14)
2
π +mπ
Anche in questo caso, per E . 2mp m
, i protoni interagiscono con i fotoni
4kT
a energie più alte e quindi il processo è poco efficiente; per le perdite di energia
saranno quindi anche qui dominanti i contributi di f ()r ) e σ()r ) intorno alla soglia
)th :
m2π c4
)r 1 + 2#r mp c2
fth =
, σth = σ ! ()r − )0 ).
(3.15)
mp c2 1 + m2#prc2
Le perdite di energia dei protoni con energie minori di 3 × 1020 eV si possono quindi
approssimare con:
!
"
1 dE
2 (kT )3 σ ! )20 − !0
−
=
e 2ΓkT ,
(3.16)
E dt pπ π 2 c4 !3 mp
37
#
dove )0 = mπ 1 +
mπ
2mp
$
è la soglia della reazione nel sistema di riferimento del
2
π +mπ
) la
protone e σ ! ≈ 6.8 × 10−36 cm2 /eV. A energie molto più alte (E / 2mp m
4kT
−28
2
sezione d’urto diventa σ()r ) ≈ 10 cm e f ≈ 0.5, quindi le perdite di energia
saranno:
1 dE
−
≈ cf σn ≈ 1.8 × 10−8 y−1 .
(3.17)
E dt
Dobbiamo infine precisare che l’approssimazione di perdite continue di energia
fatta inizialmente è giustificata dal fatto che le fluttuazioni nel processo di fotoproduzione di π modificano debolmente lo spettro (con qualsiasi indice spettrale) fino
alle energie che ci interessano (1021 eV).
3.1.1
Caratteristiche dell’interazione tra protoni e CMBR
Effetto GZK
La sezione d’urto della reazione di fotoproduzione di π vicino alla soglia ha un valore di circa 2×10−28 cm2 , mentre la densità dei fotoni della CMBR è 400 fotoni cm−3 ;
quindi una stima della lunghezza di interazione sarà data da:
λ=
1
≈ 1025 cm ≈ 5Mpc.
ρσ
(3.18)
La perdita di energia per un protone in una reazione di fotoproduzione di π è di
circa il 10%; da qui si può vedere che protoni con energie iniziali dell’ordine di 1022
eV, dopo 50 ÷ 100 Mpc vanno sotto soglia. Per questo motivo, ad energie superiori
a EGZK ≈ 7 × 1019 eV, si prevede una soppressione del flusso osservato (effetto
Greisen-Zatsepin-Kuz’min).
Si avrà quindi che il cut-off GZK per una singola sorgente dipenderà dalla distanza della sorgente stessa. Per convenzione, la soppressione GZK si definisce, per
il flusso da una distribuzione uniforme di sorgenti, come l’energia (4 × 1019 eV) a
cui comincia il ripido aumento nelle perdite di energia; in corrispondenza a questo
valore, la distanza a cui cominciano le perdite di energia per un protone a causa
−1
della fotoproduzione di π è data da (E −1 dE/cdt) ≈ 1.3 × 103 Mpc.
Bump
Immaginiamo una sorgente di protoni UHE con uno spettro differenziale a legge
di potenza, a distanza r dalla terra; i protoni si propaghino inoltre in modo rettilineo,
con un tempo di volo pari a τ = r/c. L’energia dei protoni che hanno inizialmente
E > Eb (Eb energia di cut-off) diminuisce; poichè, al diminuire dell’energia, le
perdite di energia per fotoproduzione di π si abbassano molto rapidamente, i protoni
non verranno portati a energie troppo più basse e affolleranno quindi un intervallo
di energie nei pressi di Eb . Questa ’gobba’ è ben visibile nello spettro di singola
sorgente, se questo viene moltiplicato per un fattore E 3 , come si vede in figura 3.2.
38
Flusso da singola sorgente
10
20
E3 J(E), eV2 m-2 s-1
1019
1018
1017
1016
10
15
1014
d=10Mpc
30
50
100
200
500
1000
1013 17
10
1018
1019
1020
1021
energia osservata, eV
Spettro di singole sorgenti a diverse distanze. I calcoli sono stati fatti con
Emax = 1022 eV.
Figura 3.2:
Dip
Mentre la forma del GZK risulta essere fortemente dipendente dal modello utilizzato, la forma del ‘dip’ non lo è; questa struttura è rappresentata dalla parte dello
spettro compresa tra energie di ∼ 1018 eV e ∼ 4 × 1019 eV. Per protoni con energie
minori di ∼ 4 × 1019 eV, le perdite di energia sono dominate dalla produzione di
coppia; quindi i protoni che vanno a costituire questa parte dello spettro provengono
da distanze oltre 1000 Mpc.
Per distanze maggiori di questa, l’assunzione di universo uniforme è sicuramente giustificata; possiamo infatti immaginare di vedere a queste distanze una
distribuzione uniforme di sorgenti.
Quindi ci possiamo aspettare che la forma dello spettro a energie minori di
∼ 4 × 1019 eV non sia influenzata dalla densità delle sorgenti, come si può vedere in
figura 3.3; per energie maggiori, i protoni che vanno a costituire questa parte dello
spettro provengono da distanze minori di 1000 Mpc, quindi in questo caso l’assunzione di distribuzione uniforme non può essere altrettanto giustificata.
Inoltre la soppressione del flusso che dà origine all’effetto GZK è influenzata anche dall’energia massima di accelerazione, e questi due fattori talvolta possono non
essere distinguibili.
Una discussione sull’effetto combinato dei due fattori citati sarà fornita nell’ultimo capitolo.
39
Spettro di protoni da sorgenti discrete, collocate ai vertici di una griglia cubica
a diverse distanze d [18].
Figura 3.3:
3.2
Evoluzione cosmologica
Riportiamo ora alcune informazioni sull’evoluzione cosmologica che ci serviranno
in seguito per il calcolo del flusso di raggi cosmici da sorgenti poste a distanze
cosmologiche.
La metrica che si può utilizzare in un universo omogeneo e isotropo in espansione
è quella di Robertson-Walker:
!
"
% 2
&
dr2
2
2
2 2
2
2
2
ds = dt − c R (t)
+ r dθ + sin θdφ
,
(3.19)
1 − kr2
dove le coordinate (t, r, θ, φ) sono co-moving; inoltre la coordinata r è adimensionale
e 0 ≤ r ≤ 1 mentre il fattore di scala R(t), essendo l’universo spazialmente omogeneo
e isotropo, dipende solo dal tempo e ha le dimensioni di una lunghezza. Il parametro
k individua la curvatura dell’universo: k > 0 (Ω > 1) indica un universo chiuso,
k < 0 (Ω < 1) un universo in continua espansione e k = 0 (Ω = 1) un universo
piatto. Nel seguito si considererà sempre Ω = Ωm + ΩΛ = 1, quindi k = 0.
Studiando la propagazione della luce in un universo descritto dalla metrica di
RW, si vede che se la sorgente emette un fotone con lunghezza d’onda λ1 all’istante
t1 che viene ricevuto con lunghezza d’onda λ0 all’istante t0 , vale la relazione:
λ1
R(t1 )
=
λ0
R(t0 )
(3.20)
Poichè la lunghezza d’onda del fotone che si osserva risulta aumentata, l’effetto che
si ottiene è quello di un redshift, detto redshift cosmologico.
Il parametro di redshift z è definito da:
z=
∆λ
λ0
=
−1
λ0
λ1
40
(3.21)
e perciò
λ0
R(t0 )
=
.
(3.22)
λ1
R(t1 )
Consideriamo quindi una sorgente avente luminosità assoluta L (cioè la potenza
totale irraggiata nel proprio riferimento locale di quiete) e introduciamo la distanza
dL in modo che sia:
L
d2L =
,
(3.23)
4πΦ
cioè si intende per dL la distanza che si ricaverebbe, per una sorgente di tale luminosità, se valesse la geometria euclidea e la legge 1/r2 per l’intensità della luce (Φ è
il flusso misurato); nel caso generale quindi dL non coincide con r.
Per esprimere dL in funzione di z si può procedere nel seguente modo: poichè
nel caso delle sorgenti che stiamo considerando si ha che t0 non differisce molto da
t1 (cioè le sorgenti che ci interessano sono oggetti già formati), si può sviluppare il
rapporto tra i fattori di scala cosmologici in serie di (t1 − t0 ):
1+z =
R(t0 ) + (t1 − t0 )Ṙ(t0 ) + 12 (t1 − t0 )2 R̈(t0 ) + . . .
R(t1 )
=
R(t0 )
R(t0 )
≈ 1 + H0 (t1 − t0 )
(3.24)
0)
dove H0 è la costante di Hubble (H0 = Ṙ(t
).
R(t0 )
Quindi nel caso generale la distanza dL diventa:
dL = R(t)r =
R(t0 )r
;
1+z
(3.25)
Studiando ancora la propagazione radiale della luce (ds2 = 0) e avendo preso k = 0
si ottiene la relazione che lega la distanza co-moving r al parametro di scala:
r=
/t0
cdt
=
R(t)
t
/0
dz
z
dunque
rR(t0 ) = c
/0
c
dt
(1 + z) ;
R(t0 )
dz
dz
(3.26)
dt
(1 + z);
dz
(3.27)
z
Nel caso che stiamo considerando (Ω = Ωm + ΩΛ = 1) la quantità
! "−1
2
dt
= −H0 (1 + z) (1 + z)3 Ωm + ΩΛ
dz
dt
dz
si scrive:
(3.28)
quindi, essendo zg il redshift della sorgente:
c
rR(t0 ) =
H0
/zg
0
2
dz
(1 + z)3 Ωm + ΩΛ
41
.
(3.29)
3.3
Spettro degli UHECR
Si definisce Qinj (E) lo spettro di iniezione, ovvero il numero di particelle iniettate
alla sorgente per unità di energia e nell’unità di tempo; la luminosità della sorgente
(cioè l’energia emessa in raggi cosmici dalla sorgente nell’unità di tempo) sarà data
quindi da:
E
/max
LCR =
dE E Qinj (E)
(3.30)
Emin
dove con Emin e Emax si indicano le energie minima e massima dei raggi cosmici alla
sorgente; avendo preso lo spettro di iniezione con un andamento a legge di potenza,
si può normalizzare lo spettro dei raggi cosmici in termini della luminosità L0 della
sorgente:
!
"−γ
!
"−γ
E
L0 k(γ)
E
Qinj (E) = Q0
=
(3.31)
2
Emin
Emin
Emin
dove
Quindi:
3 - #
$.−1
ln EEmax
min
k(γ) =
γ−2
γ=2
γ>2
E
/max
dE E Qinj (E) = L0 .
(3.32)
(3.33)
Emin
3.3.1
Spettro di singola sorgente
Prendiamo inizialmente una sorgente di CR posta a distanza r dall’osservatore
e trascuriamo gli effetti della cosmologia.
Vogliamo calcolare il flusso a terra di questa sorgente; per farlo dobbiamo considerare il numero di particelle che, per unità di energia, passano attraverso l’unità di
superficie nell’unità di tempo. Chiamando Eg l’energia con cui le particelle vengono
iniettate alla sorgente, il flusso a terra I(E, r) sarà dato da:
I(E, r)dE =
Q(Eg )
dEg
4πr2
e riscrivendolo per unità di angolo solido (J =
J(E, r) =
1
I)
4π
(3.34)
si ha:
1 Qinj (Eg (E, r)) dEg (E, r)
(4π)2
r2
dE
(3.35)
Dobbiamo quindi trovare l’espressione di Eg (energia con cui la particella è stata
prodotta) e della sua derivata rispetto a E (energia con cui la particella viene rivg
elata a terra). Definiamo b(Eg ) ≡ dE
≡ Eg β(Eg ) e scriviamo quindi l’equazione
dt
42
differenziale:
dEg
1 dEg
1
Eg
=
= b(Eg ) =
β(Eg );
(3.36)
dr
c dt
c
c
risolvendo tale equazione con la condizione iniziale Eg (r = 0) = E si avrà la funzione
Eg (E, r).
Trascurando l’evoluzione cosmologica, la derivata di Eg si può calcolare in questo
modo:
! "−1
dEg (E, r)
dEg (E, r) dE
b(Eg (E, r))
=
=
(3.37)
dE
dt
dt
b(E)
e lo spettro dei RC osservato a terra sarà:
J(E, r) =
1 Qinj (Eg (E, r)) b(Eg (E, r))
(4π)2
r2
b(E)
(3.38)
Spettro di singola sorgente posta a distanze cosmologiche
Analizziamo dunque il caso di una sorgente posta a distanza cosmologica, avente
redshift pari a zg e cerchiamo l’espressione del flusso osservato a terra. Dobbiamo
però considerare il fatto che l’energia rivelata è indebolita, a causa dell’espansione,
per effetto del redshift cosmologico sui singoli fotoni; questo ridurrà il flusso per un
fattore 1 + z, quindi l’espressione sarà:
I(E, zg )dE =
Q(Eg )
dEg
(1 + zg )4π(R(t0 )r)2
(3.39)
e il flusso per unità di angolo solido:
J(E, z) =
1 Qinj (Eg (E, z)) dEg (E, z)
.
(4π)2 (1 + z)(R(t0 )r)2
dE
(3.40)
Per calcolare il flusso dobbiamo ora considerare le perdite di energia; analizziamo
innanzitutto l’interazione con la CMBR osservando che la densità e l’energia dei
fotoni della CMBR aumentano con il redshift in questo modo:
n → (1 + z)3 n
E → (1 + z)E
(3.41)
e che quindi le perdite di energia possono essere valutate a qualsiasi z:
β → (1 + z)3 β;
(3.42)
perciò se β0 (E) sono le perdite di energia a z = 0 segue che:
β(E, z) = (1 + z)3 β0 ((1 + z)E).
43
(3.43)
Riscriviamo ora l’equazione differenziale per Eg :
−
1 dEg
1 dEg dz
=−
= (1 + z)3 β0 ((1 + z)Eg )
Eg dt
Eg dz dt
(3.44)
e quindi:
dEg
dt
= −(1 + z)3 Eg β0 ((1 + z)Eg ).
(3.45)
dz
dz
Per completare l’equazione differenziale per Eg bisogna aggiungere le perdite adiabatiche di energia dovute all’espansione dell’universo; se non si considerasse l’espansione si avrebbe semplicemente βad = H0 . Ora invece dobbiamo prendere in
considerazione la dipendenza di H dal tempo (e quindi da z); scriviamo quindi in
modo generico:
! "−1
1 dE dt
βad (E, z) = −
.
(3.46)
E dz dz
Abbiamo visto che la variazione dell’energia a causa della sola espansione dell’universo è data da E(z) = (1 + z)E0 e dunque si avrà:
1
βad (E, z) = −
E0
E0 (1 + z)
!
dt
dz
"−1
= H0
2
(1 + z)3 Ωm + ΩΛ .
dt
Infine, sommando i due contributi ed esplicitando dz
si ottiene:
3
4
dEg
(1 + z)2 β0 ((1 + z)Eg )
1
2
= Eg
+
dz
H0 (1 + z)3 Ωm + ΩΛ 1 + z
(3.48)
con la condizione iniziale Eg (z = 0) = E.
Resta quindi da scrivere l’espressione generale della derivata
scriviamo prima di tutto l’energia di un protone all’epoca z:
Eg (z) = E +
/t0
t
dt
5!
dE
dt
"
+
ad
!
dE
dt
"
CM BR
6
(3.47)
dEg
;
dE
.
per farlo,
(3.49)
Utilizzando dz = −H(z)(1 + z)dt e l’equazione:
b(E, z) = −
dE
= (1 + z)2 b0 [(1 + z)E] ,
dt
(3.50)
l’energia diventa:
Eg (z) = E +
/0
z
dz !
Eg (z ! ) +
!
1+z
/0
dz !
z
44
1 + z!
b0 [(1 + z ! )Eg (z ! )] .
!
H(z )
(3.51)
Differenziando rispetto a E si ottiene il fattore di dilatazione dell’intervallo di energia
y(z) = dEg (z)/dE:
y(z) = 1 +
/0
z
dz !
y(z ! ) +
1 + z!
/0
z
dz !
!
(1 + z ! )2
! db0 (E )
y(z
)
,
H(z ! )
dE !
(3.52)
dove E ! = (1 + z ! )Eg (z ! ); la corrispondente equazione differenziale è:
1 dy(z)
1
(1 + z ! )2 db0 (E ! )
=
+
.
y(z) dz
1+z
H(z ! )
dE !
(3.53)
La soluzione dell’equazione scritta sopra è proprio l’espressione generale della derivag
ta dE
:
dE


/z
! 2
!
dEg (z)
1
(1 + z )
db0 (E ) 
y(z) ≡
= (1 + z) exp 
dz ! 2
,
dE
H0
Ωm (1 + z ! )3 + ΩΛ dE !
0
dove Eg è l’energia all’epoca z.
Nelle figure che seguono si possono vedere gli andamenti di Eg (figura 3.4) e
dEg /dE (figura 3.5) in funzione dell’energia osservata per una singola sorgente a
diverse distanze.
Confrontando il grafico della figura 3.4 con le perdite di energia dei protoni (figura
3.1) si può vedere che per z molto piccoli l’energia di generazione delle particelle di
raggi cosmici rimane praticamente inalterata.
La distanza della sorgente può essere vista come R(z) ≈ (E −1 dE/dt)−1 c = β −1 c,
per cui ad un certo z si può associare un valore iniziale per la perdita di energia; nel
caso delle sorgenti più distanti (per esempio z = 0.5) si osservano due cambiamenti di
pendenza nell’energia di generazione corrispondenti ai due cambiamenti di pendenza
nel grafico di β, mentre per sorgenti più vicine si vede solo la perdita di energia
dovuta alla produzione di π.
3.3.2
Spettro da distribuzioni di sorgenti
Prendiamo ora il caso di una distribuzione uniforme di sorgenti con densità
costante n0 e stessa iniezione Qinj (Eg ) e calcoliamo il flusso a terra in questo modo:
/
n0
Qinj (Eg (E, r)) b(Eg (E, r))
Jtot (E) =
dr 4πr2
4π
4πr2
b(E)
/
1
b(Eg (E, r))
=
dr Q̃inj (Eg (E, r))
(3.54)
4π
b(E)
45
1022
Eg [eV]
1021
z=0.001
0.005
0.01
0.05
0.1
0.5
1020
1019
1018
1017 17
10
1018
1019
1020
1021
E [eV]
Energia con cui le particelle vengono iniettate alla sorgente in funzione
dell’energia di osservazione E.
Figura 3.4:
1016
1014
1012
dEg/dE
1010
z=0.001
0.005
0.01
0.05
0.1
0.5
108
106
104
102
100
1017
1018
1019
1020
1021
E [eV]
Figura 3.5:
Andamento di dEg /dE in funzione dell’energia di osservazione delle particelle.
46
avendo posto Q̃ = n0 Q; sostituendo l’espressione per b(Eg ) e assumendo particelle
relativistiche (dr = cdt) il flusso totale diventa:
/
c
b(Eg (E, r))
Jtot (E) =
dt Q̃inj (Eg (E, r))
4π
b(E)
/
c
1
=
dEg Q̃inj (Eg (E, r))
(3.55)
4π b(E)
e per la densità di CR a terra si avrà:
4π
n0
n(E) =
J(E) =
c
b(E)
/
dEg Q̃inj (Eg (E, r)).
(3.56)
Nel caso generale si deve considerare il fatto che la densità stessa delle sorgenti
dipende da z e che l’elemento di volume su cui si integra è in evoluzione cosmologica:
; ;
; ;
1 dV
3 2 ; dt ;
= (1 + z) cdL ; ; .
(3.57)
4π dz
dz
Se quindi il flusso totale per unità di angolo solido è:
1
Jtot (E) =
4π
/
dV
Q̃(Eg , z)
dEg
;
2
(1 + z)4π(rR(t0 )) dE
sostituendo la definizione di dL si avrà:
/
1
dV Q̃(Eg (E, z), z) dEg (E, z)
Jtot (E) =
;
4π
4π
(1 + z)3 d2L
dE
(3.58)
(3.59)
tenendo conto infine della variazione dell’elemento di volume con z:
1
Jtot (E) =
4π
c
=
4π
z/max
dz
0
z/max
0
Esplicitando
dt
dz
si ottiene quindi:
c
Jtot (E) =
4π
1 dV Q̃(Eg (E, z), z) dEg (E, z)
4π dz (1 + z)3 d2L
dE
; ;
; dt ;
dEg
dz ;; ;; Q̃(Eg (E, z), z)
.
dz
dE
z/max
0
(1 + z)−1 Q̃(Eg (E, z), z) dEg (E, z)
2
dz
dE
H0 (1 + z)3 Ωm + ΩΛ
47
(3.60)
(3.61)
Evoluzione cosmologica delle sorgenti
L’evoluzione cosmologica delle sorgenti, ovvero l’aumento della luminosità della
sorgente o della densità comovente con il redshift z, viene osservata in alcune classi
di oggetti astrofisici, per esempio nel caso della formazione delle stelle in galassie
normali.
Nel caso che ci interessa per l’accelerazione dei raggi cosmici, consideriamo i nuclei
galattici attivi; questi oggetti mostrano un’evoluzione rilevante nelle bande radio,
ottica e X.
L’evoluzione degli AGN osservata nella radiazione X può essere descritta in termini del fattore (1 + z)m fino a z = 1.2, con m = 2.7 [19]; nell’equazione 3.31
abbiamo definito il numero di particelle iniettate alla sorgente per unità di energia
e nell’unità di tempo: nel caso in cui consideriamo l’evoluzione cosmologica delle
sorgenti la 3.31 sarà moltiplicata per il fattore (1 + z)m :
L0 → L0 (1 + z)m .
(3.62)
Le espressioni trovate per il calcolo del flusso da una singola sorgente e da una
distribuzione uniforme saranno utilizzate in seguito per il calcolo dello spettro da
un insieme di sorgenti discrete e una distribuzione uniforme di sorgenti.
48
Capitolo 4
Esperimenti
In questo capitolo si riportano le caratteristiche principali di un raggio cosmico
primario, a partire dallo studio degli effetti dell’interazione di questo con un nucleo
presente in atmosfera. Infatti nel caso di raggi cosmici a energie oltre 1014 eV il
flusso incidente in atmosfera è troppo basso per essere rivelato, quindi vengono utilizzate tecniche indirette che permettono di risalire, dall’osservazione dello sciame
di particelle generato, alle quantità relative al primario: energia, composizione e
direzione di arrivo.
Informazioni importanti riguardo, per esempio, alla composizione chimica del
primario si possono trarre dalla componente muonica della cascata, mentre l’energia del primario è legata alla profondità in atmosfera a cui corrisponde il massimo
sviluppo della cascata.
Gli esperimenti che studiano i raggi cosmici a energie ultra-alte utilizzano varie
tecniche sperimentali per la rivelazione di questi eventi; per esempio, nel caso di
HiRes si osserva simultaneamente lo stesso sciame da due diversi rivelatori (osservazione stereo). Nel caso di Auger si utilizzano invece i rivelatori di superficie insieme
ai rivelatori di fluorescenza.
4.1
Air Showers
Un Air Shower (si può tardurre ‘sciame’) è una cascata di particelle generata
dall’interazione di un raggio cosmico primario ad alta energia al top dell’atmosfera.
Il numero di particelle all’inizio si moltiplica, poi raggiunge un massimo e si attenua
nel momento in cui le particelle scendono sotto la soglia per la produzione di ulteriori particelle.
Lo sciame è composto da tre componenti: adronica, muonica e elettromagnetica.
Se la particella primaria è nucleone o un nucleo, la cascata comincia con un’interazione adronica tra questo e, per esempio, i nuclei di ossigeno o azoto presenti in
atmosfera:
(Z, A) + p −→ (Z ! , A! ) + (Z !! , A!! ) + k p + q n + π ±,0
(4.1)
49
Figura 4.1:
Rappresentazione schematica dello sviluppo di uno sciame.
quindi ad ogni interazione il numero di adroni cresce.
Si ha inoltre che, ad ogni interazione, circa il 30% dell’energia viene trasferita
alla cascata elettromagnetica dal rapido decadimento dei mesoni neutri π 0 :
π 0 −→ 2γ,
4.1.1
τπ0 ≈ 10−16 s
(4.2)
Composizione
Componente elettromagnetica
La cascata elettromagnetica costituisce il 99.9% di tutte le particelle dello sciame;
osservando lo sciame a terra, circa il 90% sono fotoni, mentre il restante 10% è
costituito da elettroni e positroni.
La componente eletromagnetica viene alimentata quindi sia dai fotoni provenienti
dal decadimento del π 0 che fanno produzione di coppia interagendo con un nucleo
atmosferico:
γ + (Z, A) −→ (Z, A) + e+ e− ,
(4.3)
sia dai fotoni prodotti dalla bremsstrahlung di elettroni e positroni:
e− + (Z, A) −→ e− + (Z, A) + γ.
(4.4)
Successivamente, quando il tasso di energia persa per bremsstrahlung eguaglia la
perdita dovuta alla ionizzazione, l’elettrone comincia a perdere energia ionizzando
l’atmosfera.
50
Componente adronica
Il nucleone (o nucleo) uscente dalla reazione di spallazione (4.1) vista precedentemente trasporta la maggior parte dell’energia, e interagirà di nuovo nel suo
cammino.
Se, per esempio, riferendoci ad un protone, approssimiamo la sua lunghezza di
interazione in aria con il valore di 80 g/cm2 , si avrà che, per una particella che entra verticalmente in atmosfera, il numero medio di interazioni del nucleone uscente
prima di raggiungere il livello del mare è circa 12.
La fluttuazione di questo numero è una delle maggiori cause delle differenze che
si osservano tra sciami prodotti da particelle con la stessa energia del primario.
Componente muonica
I pioni carichi, prodotti nelle collisioni tra il nucleone uscente o il raggio cosmico
primario con un nucleone di un atomo di azoto o ossigeno, potranno di nuovo interagire o decadere (π ± −→ µ± + ν¯µ (νµ )).
Il fatto che un pione possa decadere prima di interagire di nuovo dipende dalla
densità dell’aria e dal fattore di Lorentz del pione; quando la distanza percorsa prima
dell’interazione eguaglia la distanza coperta prima del decadimento, le probabilità
dei due processi sono uguali:
λ
Γτ c = ,
(4.5)
ρ
dove Γ è il fattore di Lorentz del pione, che ha un tempo di decadimento pari a
τ ≈ 2 × 10−8 s, λ è la lunghezza di interazione e ρ la densità dell’aria. Quindi se
prendiamo ρ = 5 × 10−4 g/cm3 (per un’altitudine di circa 5000 m), il fattore di
Lorentz per cui si ha l’uguaglianza è circa 380, che corrisponde ad un’energia del
pione di circa 50 GeV. Per energie del π ancora maggiori i due processi avranno
probabilità uguali per valori più piccoli di ρ e quindi ad altitudini maggiori il π
tenderà a interagire piuttosto che a decadere.
I muoni prodotti nei decadimenti perdono quindi lentamente energia per ionizzazione nel loro tragitto, a differenza di elettroni e positroni, la cui quantità declina
rapidamente dopo aver raggiunto un valore massimo, a causa dei processi di produzione di coppia e di bremsstrahlung che portano l’energia verso un valore critico
oltre cui l’energia rimanente viene persa per ionizzazione.
Il numero dei muoni in uno sciame si attenua dunque molto lentamente e la
misura della componente muonica dello sciame può quindi essere utilizzata per
studiarne le caratteristiche.
4.1.2
Struttura spaziale
Le principali caratteristiche dell’air shower sono date dal suo sviluppo longitudinale, da cui si può vedere il numero di particelle create lungo l’asse dello sciame,
51
e dal profilo laterale, che descrive la distribuzione di particelle che arrivano a terra
in funzione della distanza dall’asse.
Sviluppo longitudinale
Lo sviluppo longitudinale dipende dalla quantità di atmosfera attraversata dallo
sciame, che si esprime come profondità atmosferica verticale Xv in unità di g/cm2 e
si scrive:
/∞
Xv (h) = ρ(h)dh,
(4.6)
h
dove ρ(h) è la densità dell’atmosfera all’altitudine h.
Trascurando gli effetti della curvatura terrestre, la profondità per gli sciami inclinati
con angolo θ rispetto allo zenith è:
Xv (h)
.
(4.7)
cos θ
Per analizzare lo sviluppo della cascata è utile descrivere le caratteristiche del
Toy Model sviluppato da Heitler (1949); questo modello è stato inizialmente proposto per le cascate elettromagnetiche, ma può essere applicato anche a cascate iniziate
da adroni.
Infatti, come abbiamo visto sopra, ad ogni step dello sviluppo dello sciame iniziato da un adrone si avrà uno sciame elettromagnetico a causa del decadimento dei
pioni neutri prodotti nell’interazione tra l’adrone iniziale e un nucleo dell’atmosfera.
Assumiamo che dopo una lunghezza di interazione λ (che prendiamo uguale al
cammino libero medio per la produzione di coppia), venga creata una coppia e+ e− , e
che ogni particella prenda metà dell’energia iniziale E0 . Approssimando il cammino
libero medio per la bremsstrahlung a quello per la produzione di coppia, possiamo
assumere che i processi di bremsstrahlung avvengano per ogni elettrone dopo che
questo ha percorso una distanza λ. La cascata continua e l’energia viene dimezzata
ad ogni ‘nodo’, finchè le perdite di energia per bremsstrahlung non eguagliano quelle
per ionizzazione (cioè finchè l’energia dell’elettrone non raggiunge un valore di soglia
Ec ).
Supponiamo che questo succeda ad una profondità X, per cui il numero di ‘nodi’
sarà N (X) = X/λ; il numero di elettroni e fotoni alla profondità X è dato da:
X(h, θ) =
N (X) = 2X/λ
(4.8)
e l’energia per particella:
E0
.
(4.9)
N (X)
Dunque il numero di elettroni e fotoni al massimo della cascata sarà N (Xmax ) =
E0 /Ec e la profondità a cui questo avviene:
E(X) =
Xmax = λ
ln(E0 /Ec )
.
ln 2
52
(4.10)
Figura 4.2:
Rappresentazione grafica del modello di Heitler.
Generalizzando questo modello, si può immaginare che dopo una lunghezza di interazione λ legata ad un certo processo, le particelle si moltiplichino a causa di
interazioni varie, con un numero n di particelle prodotte ad ogni moltiplicazione;
supponiamo inoltre che l’energia si distribuisca equamente tra le n particelle.
Con queste ipotesi si può immaginare di calcolare il numero di adroni presenti
in uno sciame iniziato appunto da adroni, pensando che alla prima interazione con
un nucleo atmosferico si avranno in uscita un numero n tra nucleoni e nuclei residui
della spallazione, che dopo una lunghezza di interazione λ potranno di nuovo interagire.
Quindi come prima si può calcolare il numero di particelle prodotte ad una certa
profondità X:
E0
nk =
,
(4.11)
E(X)
dove k è il numero di suddivisioni alla profondità X. Analogamente,la profondità
del massimo si troverà a:
ln(E0 /Ec )
Xmax = λ
.
(4.12)
ln n
Sviluppo laterale
L’allargamento dello sciame è dovuto a due fattori: il primo è un fattore intrinseco, in quanto è legato al fatto stesso che la particella primaria interagisce e che
le particelle secondarie non vengono prodotte in avanti; l’altro fattore è dovuto allo
scattering coulombiano multiplo delle particelle secondarie con le particelle dell’atmosfera.
Durante lo sviluppo della cascata le particelle vengono diffuse lateralmente a
causa dell’effetto combinato dei contributi spiegati sopra.
53
Per lo scattering multiplo coulombiano si ha:
! "2
< 2=
Es
δt,
δθ =
E
(4.13)
dove Es = m2e c2 (4π/α)1/2 ≈ 21MeV. L’unità di Moliere, che caratterizza l’allargamento dello sciame per particelle a bassa energia è:
r=
Es
X0 ≈ 9.3g/cm2 ,
Ec
(4.14)
che per l’aria risulta essere ∼ 0.25 lunghezze di radiazione, ovvero ∼ 78 m al livello
del mare.
Considerando un piano normale alla direzione dello sciame, la densità di particelle
a distanza r su tale piano dall’asse dello sciame è:
ρ(r, t) =
Ne (t)
f (x)
r12
(4.15)
con x = r/r1 e la parametrizzazione di f (x) data da:
xf (x) ∝ xs−1 (1 + x)s−4.5 ;
(4.16)
dove s è l’età dello sciame; questo parametro vale zero all’inizio dello sciame e diventa 1 al massimo dello sciame.
La parametrizzazione scritta sopra vale per sciami con s > 1, cioè sciami che
abbiano superato il massimo; in effetti, quando la cascata raggiunge la superficie
terrestre, ha già oltrepassato Xmax , ovvero la profondità oltre la quale prevalgono
le perdite di energia per ionizzazione. Quindi il legame accennato precedentemente
tra l’energia E0 del primario e il numero massimo di particelle nella cascata non può
essere direttamente sfruttato poichè ciò che effettivamente si misura è Ne (t) e non
Nmax = E0 /Ec .
4.1.3
Struttura temporale
Abbiamo visto che le particelle, lungo lo sviluppo dello sciame, possono essere
scatterate e quindi si allontanano dall’asse dello sciame stesso, che prosegue nel suo
sviluppo presentando un fronte curvo di particelle verso i rivelatori a terra. Possiamo
quindi immaginare la geometria laterale dello sciame come quella di un cono, e le
particelle che si trovano sulla superficie di questo arriveranno dunque con un certo
ritardo rispetto a quelle più vicine all’asse.
Il tempo di ritardo sarà proporzionale alla distanza dall’asse: trit ∝ r; poichè si ha
che la lunghezza della cascata aumenta all’aumentare di Xmax , il tempo di ritardo
permette di distinguere le cascate conoscendo Xmax .
54
Figura 4.3:
Rappresentazione di uno sciame incidente su un array di rivelatori di superficie.
4.1.4
Direzione
La direzione di arrivo della cascata viene derivata dalle misurazioni dei tempi
relativi di arrivo del fronte dello sciame sui rivelatori di superficie; si può assumere
che il fronte dello sciame, che quando arriva a terra ha uno spessore di alcuni metri,
si muova in atmosfera alla velocità della luce e che sia costituito da un piano perpendicolare alla direzione della particella incidente. Misurando il ritardo temporale
tra l’arrivo del segnale nel rivelatore i e nel rivelatore j, e conoscendo la distanza
tra i rivelatori, si può calcolare l’ampiezza dell’angolo che la direzione dello sciame
forma con lo zenith.
Nel caso di rivelatori di fluorescenza, i fotomoltiplicatori registrano la sequenza
temporale di arrivo della luce; il piano individuato dall’asse dello sciame e dal rivelatore viene ricostruito dalla sequenza dei fotomoltiplicatori illuminati.
Se la cascata viene osservata da due rivelatori di fluorescenza, si può determinare
un piano sciame-rivelatore per ogni rivelatore e l’intersezione di questi determina
direttamente la direzione senza bisogno di informazioni temporali.
55
Figura 4.4: Simulazioni della distribuzione di Xmax per sciami iniziati rispettivamente da
nuclei di ferro e da protoni con energia 1019 eV.
4.2
4.2.1
Caratteristiche del raggio cosmico primario
Composizione chimica
La profondità del massimo dello sciame riflette la composizione chimica del primario; infatti, se consideriamo il modello di sovrapposizione per i nuclei, vediamo
che ogni nucleone si comporta in media come se fosse indipendente dai restanti A-1
nucleoni. Quindi se la cascata è iniziata da un nucleo con A nucleoni, questa può
essere vista come un numero A di cascate cominciate da protoni o neutroni, la cui
energia iniziale è data da E0 /A, con E0 l’energia del nucleo.
A questo punto la profondità del massimo sarà data da:
E
A
p
p
p
Xmax
(E) = Xmax
( ) = Xmax
(E) − ln A < Xmax
(E)
A
(4.17)
quindi a parità di energia iniziale, uno sciame iniziato da un nucleo è più corto di
uno iniziato da un protone.
Il valore di Xmax (E) trovato è da intendersi come valore medio; infatti, come
si vede in figura 4.4, queste misure sono fortemente affette da fluttuazioni dovute
principalmente alla profondità e alle caratteristiche della prima interazione. Le fluttuazioni nelle interazioni successive sono mediate su un numero molto grande di
particelle e quindi non sono importanti.
Un altro fattore importante per lo studio della natura del primario è, come
detto in precedenza, la componente muonica dello sciame. Poichè il contenuto di
muoni si attenua più lentamente rispetto a quello degli elettroni, la piattezza della
distribuzione del numero di muoni sarà meno affetta da fluttuazioni, e dunque in
questo caso la misura dell’energia del primario risulterà migliore.
56
Un problema legato alla rivelazione dei muoni riguarda proprio il fatto che la
loro quantità non si moltiplica, e quindi il numero di muoni in uno sciame è minore
di quello degli elettroni e positroni.
Considerando l’approssimazione di sovrapposizione descritta sopra, per uno sciame iniziato da un nucleo ci si può aspettare di avere un contenuto di muoni maggiore
rispetto ad uno sciame iniziato da un protone con la stessa energia; questo perchè
l’energia media dei pioni creati nelle collisioni è più bassa nello sciame iniziato dal
nucleo che in quello iniziato dal protone perchè l’energia per nucleone è più bassa.
La forma generale (ottenuta da simulazioni) del numero totale di muoni a basse
energie in uno sciame è la seguente:
! "α
E0
Nµ (> 1GeV) ∝ A
(4.18)
A
dove si prende α = 0.86; quindi a parità di energia del primario, uno sciame iniziato
da un nucleo di ferro (A=56) avrà circa il 75% di muoni in più rispetto ad uno
iniziato da un protone.
4.2.2
Energia
Abbiamo visto che il numero di particelle in uno sciame è in relazione con l’energia della particella primaria; si può quindi pensare di misurare il numero di particelle
che arrivano a terra ad una distanza fissata dall’asse dello sciame. Questo è il procedimento che viene adottato nel caso dei rivelatori di superficie.
E’ necessario quindi conoscere la funzione di distribuzione laterale dello sciame,
che mette in relazione il numero Ne di elettroni nella cascata con la densità della
stessa ad una certa distanza dall’asse; la misura del numero di particelle è però il
risultato di un campionamento, in quanto l’area sensibile dell’esperimento è minore
dell’area totale disponibile, ovvero i rivelatori di superficie non potranno intercettare
tutte le particelle che arrivano a terra.
Per un array di rivelatori, simulazioni Monte Carlo hanno dimostrato che la
densità di particelle a distanze 400-1200 m dal core è proporzionale all’energia del
primario:
E0 ∝ ρ(r).
(4.19)
La quantità totale della luce di fluorescenza generata in atmosfera durante lo
sviluppo di uno sciame può essere sfruttata come misura calorimetrica dell’energia
della cascata elettromagnetica e quindi del raggio cosmico primario.
I rivelatori di fluorescenza guardano le tracce di luce rilasciate in atmosfera dalle
particelle secondarie che collidono con molecole dell’aria (per esempio molecole di
azoto) eccitandole; le molecole si diseccitano poi riemettendo radiazione nell’UV,
che viene quindi raccolta dai rivelatori di fluorescenza. L’intensità della luce di fluorescenza è praticamente proporzionale al numero di particelle cariche che eccitano le
57
molecole dell’atmosfera, ma poichè si ha anche che il numero di e+ , e− è dominante,
si può considerare l’intensità della radiazione di fluorescenza proporzionale a Ne (x).
L’energia totale della componente elettromagnetica si determina dunque integrando il profilo longitudinale dello sciame:
! "
/
dE
EEM =
dx
Ne (x)
(4.20)
dx ion
e, poichè le particelle viaggiano a velocità v ≈ c, l’energia diventa:
/
2 MeV
EEM ≈
dx Ne (x)
g/cm2
(4.21)
Per descrivere la forma di Ne (x) si utilizza una funzione empirica del tipo:
!
"(Xm −X0 )/λ
X − X0
Ne (x) = Nm
exp(Xm −X0 )/λ ,
(4.22)
Xm − X0
(Gaisser-Hillas), dove X è la profondità atmosferica, X0 è la profondità della prima
interazione, Xm è la profondità quando lo sciame ha raggiunto il numero massimo
di particelle (Nm ).
L’energia della componente elettromagnetica rappresenta un limite inferiore per
l’energia del primario; sono infatti da considerare le quantità di energia che vanno in
muoni e neutrini atmosferici, il cui numero dipende dalla natura della particella che
inizia la cascata, e anche la luce Čerenkov diretta e scatterata prodotta durante lo
sviluppo dello sciame. Quest’ultima deve essere stimata e sottratta dal flusso totale,
cosı̀ come devono essere stimati i fenomeni di attenuazione e di scattering subiti dai
fotoni in atmosfera.
4.3
Accettanza
Le caratteristiche degli apparati di misura a terra determinano la possibilità
di misurare una certa parte dello spettro in energia dei raggi cosmici; i conteggi
effettuati dall’apparato dipendono dal flusso di raggi cosmici all’energia dello sciame
considerato e dall’apertura effettiva dell’apparato. L’apertura effettiva del rivelatore
sarà data da:
Aef f = AT.
(4.23)
L’apertura A del rivelatore si può scrivere come A = Sπ sin2 θ, dove S è la superficie
dell’array di rivelatori nel caso dei rivelatori di superficie o l’area dello specchio nel
caso di un rivelatore di fluorescenza e θ è l’angolo massimo, rispetto allo zenith,
di sensibilità del rivelatore; il duty cycle T è la frazione di tempo durante la quale
l’apparato può essere effettivamente utilizzato.
Il numero di conteggi del rivelatore per unità di tempo R sarà quindi:
R = ΦAef f ,
58
(4.24)
dove Φ indica il numero di particelle per unità di tempo, angolo solido e superficie.
4.4
Esperimenti
Per investigare sull’origine e i meccanismi di produzione dei raggi cosmici, gli
esperimenti nelle regioni a energie più alte misurano tre quantità: energia del primario, composizione e direzione di arrivo.
La misura diretta delle caratteristiche del primario risulta impossibile a energie
maggiori di 1014 eV, dove il flusso di raggi cosmici incidente sull’atmosfera è molto
basso per essere rivelato; a queste energie, quindi, gli esperimenti utilizzano delle
tecniche indirette che permettono di risalire, misurando i parametri della cascata
prodotta, alle quantità elencate sopra.
I rivelatori di superficie raccolgono le particelle che arrivano a terra, determinando l’energia del primario dalla densità di particelle, la direzione di arrivo dai tempi
di trigger del rivelatore, e possono studiare la natura del primario dal rapporto tra
la componente muonica e quella elettronica.
I rivelatori di fluorescenza, come già accennato precedentemente, raccolgono la
luce di fluorescenza prodotta in atmosfera; con questi si può quindi studiare il profilo
longitudinale dello sciame.
4.4.1
AGASA
L’Akeno Giant Air Shower Array (AGASA) si trova presso l’osservatorio di
Akeno in giappone; l’array consiste di 111 scintillatori di 2.2 m2 collocati in superficie per misurare la densità di particelle cariche e di 27 rivelatori posti sotto
materiali assorbenti per misurare la componente muonica dello sciame. L’area totale coperta da AGASA è di 100 km2 .
Questo esperimento è rimasto operativo fino al gennaio del 2004.
4.4.2
Fly’s Eye e HiRes
Il rivelatore Fly’s Eye è collocato a Dugway, nello Utah; consiste di due array di
specchi parabolici, ognuno con dei fototubi nel piano focale. Gli specchi sono posti
in modo tale da coprire tutto il cielo notturno, con ogni fototubo che ne guarda una
porzione esagonale.
I fototubi raccolgono la luce di fluorescenza dell’azoto e la luce Čerenkov; mentre la luce Čerenkov è fortemente direzionale, poichè emessa entro un angolo ben
definito rispetto alla traiettoria dell’elettrone, la luce di fluorescenza proviene da un
meccanismo di diseccitazione delle molecole, e viene emessa isotropicamente. Per
questo motivo, la rivelazione dello sciame può avvenire anche a grandi distanze.
E’ necessario, quindi, conoscere l’efficienza della fluorescenza, ovvero il numero
59
Figura 4.5:
Mappa del sito dell’osservatorio Pierre Auger in Argentina.
di fotoni prodotti per particella carica per unità di tragitto percorso in atmosfera;
oltre a questo, bisogna considerare il fatto che sia la luce di fluorescenza che la luce
Čerenkov possono subire scattering e essere assorbite.
Come detto precedentemente, servendosi di osservazioni simultanee dello stesso
sciame dai due diversi rivelatori (osservazione stereo), la geometria dell’EAS può
essere determinata più precisamente calcolando l’intersezione dei due piani sciamerivelatore.
L’osservatorio HiRes (High Resolution Fly’s Eye) è lo stadio successivo dell’esperimento Fly’s Eye, che è rimasto operativo fino a aprile 2006.
4.4.3
Auger
L’osservatorio Pierre Auger è collocato nei pressi della città di Malargüe in Argentina; la latitudine di 35° permetterà una copertura completa quando sarà combinato con il sito nell’emisfero nord; inoltre il luogo scelto ha un’area pianeggiante
di più di 3000 km2 , superficie necessaria per la rivelazione di circa 2500 eventi oltre
1019 eV e di circa 120 eventi sopra 1019.5 eV per anno. Si può calcolare che se non
esistesse la soppressione del flusso di raggi cosmici ultra-energetici prevista dall’effetto GZK, l’Osservatorio Pierre Auger sarebbe in grado di rivelare circa 50 eventi
all’anno per energie superiori a 1020 eV; finora è stato osservato un solo evento oltre
questa energia.
L’altitudine di 1400 m sul livello del mare pone il sito vicino al massimo dello
sviluppo per uno sciame verticale di energia 1018 eV. Per quanto riguarda le condizioni atmosferiche e climatiche, la copertura nuvolosa del cielo notturno assicura
rendimenti ragionevoli per i rivelatori di fluorescenza, mentre la visibilità è buona,
non essendo significativamente presente l’inquinamento luminoso.
60
I rivelatori di fluorescenza sono situati ai 4 lati dell’array di rivelatori di superficie; ogni FD contiene 6 telescopi ottici di tipo Schmidt, ognuno con un campo di
vista di 30°×30°: di conseguenza utilizzando 6 telescopi da ogni postazione sono
visibili 180° in azimuth.
I telescopi consistono di specchi sferici che focalizzano la luce di fluorescenza in
una camera, rappresentata da una una griglia di 440 fotomoltiplicatori in configurazione esagonale posta nel piano focale. Ogni pixel osserva un angolo solido di
1.5°×1.5°.
Davanti ai telescopi sono presenti dei filtri ottici per rimuovere la maggior parte
della luce al di fuori della banda di fluorescenza dell’azoto; inoltre i telescopi hanno
un’incertezza di 0.1° rispetto alla direzione nominale verso cui puntano.
Ad ogni camera è attaccato un sistema di acquisizione dati che registra il segnale
dei fotomoltiplicatori, che viene campionato a intervalli di 100 ns.
Per quanto riguarda il processo di ricostruzione, la luce raccolta dal telescopio
deve essere trasformata nel quantitativo di luce emessa lungo l’asse dello sciame in
funzione della profondità. A questo scopo, è necessario conoscere accuratamente
le condizioni atmosferiche locali; si devono quindi conoscere la distribuzione degli
aerosols e la densità dell’atmosfera a diverse altitudini.
Poichè gli FD possono essere utilizzati soltanto in notti senza luna, in presenza
di buone condizioni atmosferiche, il rendimento dei rivelatori di fluorescenza è del
10%.
La quantità di luce emessa lungo lo sviluppo dello sciame viene calcolata utilizzando la geometria dello sciame, le condizioni atmosferiche, lo spettro della luce e la
relativa risposta del detector; si deve inoltre tener conto della luce Čerenkov diretta
e scatterata misurata dall’FD. Dalla luce di fluorescenza si risale quindi all’energia
depositata dallo sciame conoscendo il prodotto di fluorescenza in funzione della profondità.
I rivelatori di superficie dell’osservatorio Pierre Auger consistono di 1600 contenitori riempiti con 12 t di acqua purificata per la rivelazione della luce Čerenkov a
distanza di 1.5 km l’uno dall’altro e organizzati in una griglia triangolare su un’area
di 3000 km2 ; i contenitori hanno forma cilindrica (3.6 m di diametro e 1.2 m di
altezza), con una superficie superiore di 10 m2 .
L’area del contenitore è appositamente scelta per le densità attese di particelle
(∼ 1/m2 a 1 km dall’asse dello sciame) e l’altezza dell’acqua (1.2 m), corrispondente
a 3.5 lunghezze di radiazione dell’elettrone, è stata scelta per assorbire almeno il
90% delle particelle elettromagnetiche incidenti. Ogni contenitore è osservato da 3
fotomoltiplicatori posti a intervalli di 120°.
La tecnica utilizzata dll’SD permette una ricostruzione più accurata della geometria dello sciame, se si confronta con il metodo dell’FD. Inoltre se si considera
il fatto che i rivelatori di fluorescenza funzionano solo in determinate condizioni, il
numero di eventi registrati con gli SD a parità di area è molto più grande.
Lo svantaggio in questo caso è legato al fatto che le caratteristiche dello sciame
61
Figura 4.6: Esempio di due EAS visti dall’SD; la grandezza dei cerchi rappresenta la densità
di particelle misurata nei rivelatori.
possono essere investigate soltanto attraverso simulazioni Monte-Carlo.
Attraverso l’utilizzo della tecnica ibrida, gli svantaggi che comporta l’utilizzo individuale di ogni metodo vengono compensati dai vantaggi dell’altro.
Nella figura 4.6 sono mostrati alcuni esempi degli EAS visti dall’SD; il diametro
dei cerchi indica la densità delle particelle rivelate nei rispettivi tanks; l’energia e la
posizione dell’asse sono ricostruite da un fit della funzione di distribuzione laterale
(LDF) rispetto alla densità delle particelle vista nei diversi rivelatori. Per esempio,
nella figura 4.7 si vede la LDF ricostruita per l’EAS della figura 4.6 in basso.
Simulazioni sugli EAS hanno mostrato che l’energia del primario, nell’intervallo
di energie considerato, è determinata al meglio dal valore della LDF a distanze di
1000 m dall’asse dello sciame; questo numero, generalmente chiamato S(1000), è il
valore meno affetto dalle fluttuazioni causate sia dallo sviluppo longitudinale dello
sciame che dalla massa della particella primaria.
Oltre alla densità delle particelle ricostruita dai segnali integrati nei rivelatori
di superficie, si possono trarre informazioni importanti anche dalle caratteristiche
temporali delle tracce dei segnali registrati. Infatti in sciami molto inclinati la componente elettromagnetica risulta essere assorbita in parte molto maggiore rispetto a
sciami verticali, dove si possono osservare molti elettroni con un profilo temporale
più allargato.
Nei rivelatori di fluorescenza, gli sciami di raggi cosmici sono visti come una
sequenza di pixels illuminati nella camera. Un esempio di un evento che si propaga
in due telescopi adiacenti si può vedere in figura 4.8.
Il primo passo nell’analisi
62
Figura 4.7:
Funzione di distribuzione laterale ricostruita per l’EAS di 4.6
Traccia di luce rilasciata da un evento in due camere adiacenti; i diversi colori
indicano la progressione temporale di accensione dei pixels nelle rispettive camere.
Figura 4.8:
63
Figura 4.9:
Geometria della traiettoria di un EAS.
di un evento nell’FD è la determinazione del piano sciame-rivelatore (SDP) ricostruito dalla direzione di vista dei pixels della camera; l’asse dello sciame che giace nel
SDP è definito dal parametro d’impatto Rp e dall’angolo rispetto all’orizzontale χ0 .
Successivamente, le informazioni temporali vengono utilizzate per ricostruire l’asse
dello sciame entro il piano SDP.
Per una data geometria, il tempo di arrivo ti della luce al pixel i è dato da:
ti = t0 +
Rp
tan [(χ0 − χi )/2] .
c
(4.25)
L’incertezza dei tre parametri dipende dalla particolare geometria dell’evento e dalla
lunghezza della traccia osservata, e questa incertezza si traduce in incertezza nella
ricostruzione dell’energia dello sciame.
Un modo per migliorare la ricostruzione dell’energia dello sciame è quello di
combinare le informazioni date dai rivelatori di superficie con quelle dei rivelatori
di fluorescenza (ricostruzione ibrida); con l’ausilio delle informazioni temporali dei
rivelatori di superficie è possibile ridurre le incertezze nella ricostruzione dell’asse
di 50 m nella posizione del core e 0.5° nell’orientazione dell’asse. Le informazioni
temporali tGN D da una stazione colpita a terra possono essere messe in relazione
con il tempo t0 a cui lo sciame raggiunge la posizione di massimo avvicinamento al
telescopio:
! GN D · Ŝ)/c.
t0 = tGN D − (R
(4.26)
! GN D denota la direzione della stazione colpita e Ŝ il vettore unitario dell’asse
Qui R
dello sciame.
64
Dal momento che l’SD opera al 100% del suo rendimento, molti degli eventi osservati dall’FD sono di fatto eventi ibridi, con l’eccezione di quelli a basse energie. In
tali analisi la sincronizzazione temporale tra i diversi rivelatori è molto importante;
per controllare la procedura di ricostruzione vengono generati eventi artificiali dalla
cental laser facility.
65
Capitolo 5
Anisotropia
Lo spettro di raggi cosmici risulta essere essenzialmente isotropo fino a energie di
circa 1018 eV; per energie più alte ci si aspetta di osservare effetti legati all’anisotropia
delle sorgenti di raggi cosmici, in quanto il campo magnetico galattico non è più in
grado di deviare le traiettorie delle particelle in modo abbastanza significativo da
rendere isotropa la distribuzione delle direzioni di arrivo.
Se i raggi cosmici a energie più alte sono per lo più protoni e nuclei, solo le
sorgenti che sono più vicine di 200 Mpc possono contribuire al flusso osservato sopra
6×1019 eV; protoni a energie più alte interagiscono con la radiazione cosmica di fondo
producendo pioni, processo che provocherebbe un’attenuazione del flusso proveniente
da sorgenti più distanti.
Nei modelli top-down il problema dell’energia è risolto postulando l’esistenza di
particelle X di materia oscura con massa mX ≥ 1012 GeV e vita media τX ≥ 1010
anni; dal decadimento di tali particelle potrebbe avere origine lo spettro di UHECR,
dominato in questo caso da fotoni ad alta energia.
L’ipotesi che gli UHECR siano di origine locale nella nostra galassia sarebbe
sostenibile nel caso in cui la concentrazione di materia oscura fosse abbastanza alta
nell’alone della galassia; in questo modo si potrebbe spiegare l’eccesso di AGASA,
ovvero 11 eventi con energie maggiori di 1020 eV.
Nel caso in cui raggi cosmici ad energie cosı̀ alte siano prodotti all’interno della
galassia non ci si può aspettare di vedere l’effetto GZK.
L’osservazione di tale attenuazione nello spettro di Auger e di HiRes mette in
secondo piano le teorie top-down rispetto alle bottom-up, secondo cui l’origine degli
UHECR è legata a meccanismi astrofisici e non al decadimento di particelle di materia oscura.
D’altra parte, l’attenuazione che si osserva nel flusso non basta da sola come
verifica della previsione GZK; una diminuzione del flusso di raggi cosmici analoga a
quella che si avrebbe grazie all’effetto GZK, si potrebbe osservare nel caso in cui le
sorgenti stesse non fossero in grado di accelerare particelle oltre una certa energia.
66
Anche in questo caso, quindi, lo spettro mostrerebbe un cut-off.
L’evidenza fornita dalla soppressione del flusso deve dunque essere supportata
dalla conoscenza delle sorgenti acceleranti; nel caso in cui si possa dimostrare che
i raggi cosmici giungano da un certo tipo di oggetti con caratteristiche tali da permettere l’accelerazione fino alle energie più alte, l’insieme di queste informazioni
costituirebbe una verifica della previsione dell’effetto GZK.
Se ipotizziamo che i raggi cosmici più energetici provengano da sorgenti relativamente vicine e distributite in modo non uniforme, ci possiamo aspettare di osservare
un’anisotropia nelle direzioni di arrivo degli eventi, nel caso in cui questi siano abbastanza energetici da non subire in modo significativo la deflessione del campo
magnetico galattico. Questa anisotropia viene effettivamente osservata, sia tramite
l’osservazione di eventi con direzioni di arrivo molto ravvicinate, sia con la correlazione delle direzioni di arrivo con un certo tipo di oggetti astronomici.
L’esperimento Auger dimostra l’anisotropia sulla base della correlazione tra le
direzioni di arrivo dei raggi cosmici con le energie più alte misurate dall’Osservatorio e le posizioni dei nuclei galattici attivi (AGN) più vicini, tratte dalla dodicesima
edizione del catalogo di quasars e nuclei attivi di Veron-Cetty e Veron (VCV).
Con lo stesso metodo di ricerca delle correlazioni utilizzato in Auger sono state
analizzate le correlazioni anche nell’esperimento HiRes, concludendo però che non
esiste una correlazione significativa tra i dati di HiRes e gli AGN del catalogo VCV.
In questo capitolo si analizzano alcuni dettagli sul metodo utilizzato per lo studio dell’anisotropia in Auger e inoltre si discutono alcune possibili implicazioni del
segnale di correlazione osservato.
Si riportano infine alcune proposte per l’utilizzo di cataloghi alternativi a VCV.
5.1
Evidenze di anisotropia degli UHECR
Nelle sezioni che seguono si riportano alcune evidenze dell’anisotropia nelle direzioni di arrivo dei raggi cosmici a energie ultra alte; nel paragrafo 5.1.1 si analizza
la correlazione trovata dall’esperimento Auger con le posizioni dei nuclei galattici
attivi del catalogo Veron-Cetty e Veron (VCV), spiegando i criteri utilizzati nella
ricerca.
Nel paragrafo 5.1.2 si spiega la possibilità di dimostrare l’anisotropia attraverso
la misura dell’intensità dei raggi cosmici da diverse direzioni nel cielo.
Nel paragrafo 5.1.3 si analizza un metodo per costruire, a partire da un catalogo
di sorgenti, una mappa di probabilità delle direzioni di arrivo dei raggi cosmici oltre
una certa energia.
67
Proiezione della sfera celeste in coordinate galattiche con finestre circolari centrate nelle posizioni dei 442 AGN (292 entro il campo di vista di Auger) con z < 0.017 dal
catalogo VCV. La probabilità p è data dalla frazione di cielo accessibile all’osservazione
da Auger, coperta da finestre circolari di ampiezza ψ centrate sulle sorgenti selezionate.
Figura 5.1:
5.1.1
Correlazione con Nuclei Galattici Attivi
Gli AGN sono da lungo tempo considerati possibili siti per la produzione di
particelle energetiche, dove protoni e nuclei potrebbero essere accelerati fino alle più
alte energie misurate.
Immaginando di mettere una finestra di alcuni gradi attorno ad ogni AGN noto
entro 100 Mpc, si vede che viene ricoperta una significativa frazione di cielo, ma non
la maggior parte di esso. Da qui la motivazione per la ricerca di un eccesso di raggi
cosmici, rispetto a ciò che ci si aspetterebbe se il flusso fosse isotropo, con direzioni
di arrivo vicine alle posizioni degli AGN.
La parte sud dell’osservatorio Pierre Auger è situata a Malargue, in Argentina,
alla latitudine 35.2° S, longitudine 69.5° W, ad un’altitudine media di 1400 m sul
livello del mare. Il set di dati analizzati per lo studio delle correlazioni consiste di
eventi registrati all’osservatorio dal 1 gennaio 2004 al 31 agosto 2007; durante questo
periodo, il numero di rivelatori di superficie è aumentato da 154 a 1388.
Si considerano eventi la cui energia ricostruita è di 40 EeV e il cui angolo di
zenith è minore di 60°.
Metodo di ricerca della correlazione in Auger
Assumendo l’ipotesi di isotropia delle direzioni di arrivo dei raggi cosmici, possiamo calcolare la probabilità che un dato raggio cosmico arrivi per caso entro una
distanza angolare fissata da un qualsiasi AGN.
La probabilità p che un evento da una distribuzione isotropa abbia per caso una
68
direzione di arrivo più vicina di una certa distanza angolare da un qualsiasi membro
di un insieme di candidati a sorgenti puntiformi è data dalla frazione del cielo accessibile all’osservazione da Auger, coperta da finestre circolari di ampiezza ψ centrate
sulle sorgenti selezionate.
Ad alte energie l’esposizione dei rivelatori di superficie di Auger dipende soltanto dalla declinazione, quindi questa probabilità può essere calcolata integrando la
funzione di esposizione (Appendice C) su tutte le direzioni nel cielo che diano una
correlazione positiva:
/
p=
ω(δ) cos(δ)dδdα
(5.1)
A
dove α e δ si riferiscono alle coordinate celesti, ω è la funzione di esposizione e l’area
A è la frazione di cielo coperta dalle finestre circolari centrate sulle sorgenti.
La probabilità che un numero k di eventi su un totale di N da un flusso isotropo
abbiano direzioni di arrivo entro ψ rispetto alle sorgenti candidate è data dalla
distribuzione binomiale cumulativa:
"
N !
>
N
P =
pj (1 − p)N −j .
(5.2)
j
j=k
Per questa analisi sono stati considerati come candidati a sorgenti di raggi cosmici
gli AGN presenti nella 12a edizione del catalogo di quasars e nuclei attivi di VeronCetty e Veron (VCV) [6]. Questo catalogo non contiene tutti gli AGN esistenti,
ma risulta dall’insieme di tutti gli oggetti presenti in letteratura; contiene 85221
quasars, 1122 BL Lac e 21737 galassie attive.
Tra questi oggetti, 694 hanno redshift z ≤ 0.024, un valore corrispondente a
distanze minori di circa 100 Mpc. A distanze maggiori di questa il catalogo diventa
sempre più incompleto e disomogeneo; inoltre risulta incompleto sul piano galattico.
Questo non è un ostacolo per la dimostrazione dell’esistenza dell’anisotropia, ma
può influire sull’identificazione non ambigua del tipo di sorgenti acceleranti.
Il grado di correlazione tra UHECR e AGN è funzione di tre parametri: il redshift
massimo dell’AGN zmax , la separazione angolare massima ψ e la soglia in energia
per i raggi cosmici Eth ; la scansione in energia è motivata dall’assunzione che i raggi
cosmici più energetici siano quelli che vengono meno deflessi dai campi magnetici e
che hanno probabilità minore di giungere da sorgenti molto distanti a causa dell’effetto GZK. Questa selezione in energia viene quindi fatta cominciando dall’evento
più energetico e aggiungendo uno ad uno gli eventi con energia decrescente.
Con i dati raccolti tra il 1 gennaio 2004 e il 27 maggio 2006 è stata fatta una
ricerca esplorativa di correlazione; la probabilità minima Pmin è stata trovata in
corrispondenza del set di parametri: zmax = 0.018 (corrispondente ad una distanza
massima di 75 Mpc), Eth = 56 EeV e ψ = 3.1, con 12 eventi su 15 correlati con
almeno un AGN selezionato. Per questo set di parametri, la correlazione casuale è
69
Proiezione della sfera celeste in coordinate galattiche con cerchi di 3.2° centrati
nelle direzioni di arrivo dei 27 raggi cosmici rivelati dall’osservatorio Pierre Auger con
energie E > 57 EeV. Le posizioni dei 442 AGN (292 entro il campo di vista di Auger) con
z < 0.017 dal catalogo VCV sono indicate con asterischi. La linea continua rappresenta il
confine del campo di vista dell’Osservatorio (con angolo di zenith minore di 60°); la linea
tratteggiata delimita il piano supergalattico. L’aumento nell’intensità del colore indica
una maggiore esposizione relativa. [32]
Figura 5.2:
data da p = 0.21, quindi se il flusso fosse isotropo ci potremmo aspettare solo 3.2
eventi in correlazione casuale.
La probabilità Pmin trovata nella ricerca esplorativa è pari a 2 × 10−6 ; in realtà
questo valore deve essere corretto a causa del numero di tentativi fatti per trovare la
probabilità minima a posteriori, e la probabilità minima risulterà dunque più alta.
Per evitare questo si ricorre ad una procedura di analisi definita a priori.
La correlazione osservata nella ricerca esplorativa ha motivato la costruzione di
uno specifico test per rigettare o accettare l’ipotesi di isotropia con parametri specificati a priori su un set di dati indipendente.
L’ipotesi zero è data in questo caso dall’isotropia della distribuzione delle direzioni di arrivo; si definiscono due tipi di errori, che consistono nel rigettare erroneamente l’ipotesi zero (errore di tipo I), ovvero è la probabilità α di dichiarare
il set di dati indipendenti anisotropo quando non lo è, ed è stata scelta α = 1%.
L’errore di tipo II è la probabilità di accettare incorretamente l’ipotesi nulla, ovvero
la probabilità β di dichiarare isotropo il set di dati indipendenti quando non lo è (è
detta anche potenza del test), ed è stata scelta β = 5%.
Per mantenere una potenza del test al livello desiderato (β = 5%), si definisce
il periodo della prescrizione come il tempo necessario per la rivelazione di un certo
numero di eventi che superino i criteri di selezione. Dal momento che non si può
prevedere quanti eventi sarebbero richiesti per confermare i risultati ad un livello
statisticamente significativo per per la ricerca esplorativa, è stata adottata una prescrizione continuativa (running prescription) per condurre un’analisi sequenziale.
70
N
kmin
4
4
6 8 10 12 . . .
5 6 7 8 ...
30 31 33 34
14 14 15 15
Criteri per la running prescription; N corrisponde al numero di eventi con
E > 56 EeV osservati durante l’analisi sequenziale e kmin è il numero minimo di eventi
entro la finestra angolare (ψ = 3.1) e massimo redshift degli AGN (zmax = 0.018) richiesti
per rigettare l’ipotesi di isotropia con un livello di confidenza di almeno il 99%. Questa
prescrizione, applicata sui dati registrati dopo il 27 maggio 2006, è stata soddisfatta con
N = 8 e k = 6 il 25 maggio 2007.
Tabella 5.1:
Poichè si applica un test dopo ogni rivelazione, la soglia di ogni test individuale deve essere minore della soglia di prescrizione globale α. In pratica questo
significa che si annuncia l’evidenza di una correlazione al momento della rivelazione
dell’evento n se il numero di eventi k che correlano con gli AGN tra questi n dà una
probabilità cumulativa P minore di un certo valore.
La prescrizione applicata ai dati collezionati dopo il 27 maggio 2006 è stata soddisfatta il 25 maggio 2007 con N = 8 e k = 6 (tabella 5.1).
Avendo stabilito che esiste un’anisotropia in accordo con una ricerca a priori su
un sottoinsieme dei dati di Auger, consideriamo ora i risultati utilizzando l’intero
set di dati di Auger (1 gennaio 2004 - 31 agosto 2007), che permette di ottenere misure più accurate del segnale di correlazione; utilizzando lo stesso metodo descritto
sopra si trova che la probabilità minima per l’ipotesi di distribuzione isotropa delle
direzioni di arrivo corrisponde al set di parametri: zmax = 0.017 (Dmax ≈ 75 Mpc),
Eth = 57 EeV e ψ = 3.2.
Con questi parametri, si trova che 20 dei 27 eventi più energetici sono in correlazione con almeno uno dei 442 AGN selezionati (sono le sorgenti nel catalogo
con z ≤ 0.017, e di queste 292 sono nel campo di vista dell’osservatorio), mentre
ne sarebbero previsti 5.6 in media se il flusso fosse isotropo (p=0.21). La rispettiva probabilità cumulativa di raggiungere questo livello di correlazione da un flusso
isotropo è data da Pmin = 4.6 × 10−9 . Di nuovo, la Pmin trovata deve essere corretta,
come nel caso della ricerca esplorativa, per il numero di tentativi fatti per trovare
la probabilità minima a posteriori; considerando queste correzioni, Pmin diventa
dell’ordine di 10−5 .
5.1.2
Angular power spectrum
Come accennato in precedenza, l’anisotropia dei raggi cosmici può essere dimostrata analizzando le deviazioni dall’isotropia nella distribuzione delle direzioni
di arrivo.
Per un qualsiasi set di dati di direzioni di arrivo (con un’esposizione a tutto
cielo), l’anisotropia può essere caratterizzata da un set di coefficienti a)m dati da:
/
a)m =
I(θ, φ)Y)m (θ, φ)dΩ
(5.3)
71
dove le Y)m (θ, φ) sono le armoniche sferiche e I(θ, φ) è l’intensità dei raggi cosmici
in una data direzione.
Per un numero N discreto di direzioni di arrivo con un’esposizione relativa ω(!u)
non uniforme, la stima per i coefficienti è data da:
a)m =
N
1 > 1
Y)m (!u(i) )
N i=1 ωi
(5.4)
dove ωi è l’esposizione relativa nella direzione di arrivo !u(i) e N è la somma dei pesi
1
.
ωi
L’angular power spectrum è il valor medio di a2)m in funzione di 5:
)
>
1
C) =
a2 ,
25 + 1 m=−) )m
(5.5)
quindi la potenza nel modo 5 = 1/θ è sensibile a variazioni di flusso su una scala
angolare di θ radianti. Per studiare l’anisotropia dei raggi cosmici si considerano i
modi da 5 = 1 (termine di dipolo) a 5 ∼ 60, essendo gli ordini più alti irrilevanti per
la sensibilità dei rivelatori; per i raggi cosmici carichi la diffusione dovuta ai campi
magnetici complica le cose.
Analizzando i primi modi, possiamo vedere che una distribuzione di intensità
che contiene solo il termine di monopolo è equivalente alla distribuzione isotropa; la
misura dell’anisotropia è data proprio dall’intensità degli altri termini di multipolo
relativamente a quello di monopolo.
Una distribuzione puramente dipolare non è possibile perchè l’intensità dei raggi
cosmici non può essere negativa in metà del cielo; quando si parla di termine di
dipolo si intende quindi una deviazione dipolare dall’isotropia. Ciò si potrebbe
avere se le sorgenti fossero distribuite in un alone attorno alla Galassia, e in questo
caso il vettore di dipolo punterebbe verso il centro galattico.
Una approssimativa deviazione dipolare dall’isotropia si può avere nel caso di
una sola sorgente forte, se la diffusione magnetica distribuisce quelle direzioni di
arrivo sulla gran parte del cielo.
Per una deviazione dipolare dall’isotropia, l’intensità dei raggi cosmici varia nel
cielo in questo modo:
N
! · !u).
I(!u) =
(1 + αD
(5.6)
4π
N
Qui !u è il vettore unitario che definisce la direzione celeste, 4π
è l’intensità media,
!
D è il vettore unitario che definisce la direzione del dipolo e α è la sua ampiezza, il
cui valore dà una misura dell’anisotropia:
α=
Imax − Imin
.
Imax + Imin
72
(5.7)
L’applicazione di questo metodo alle direzioni di arrivo degli eventi rivelati da
Auger con energie oltre 50 EeV mostra che è necessario un ordine di multipolo pari
a 5 per descriverne la distribuzione con un livello di confidenza pari al 99%.
5.1.3
Mappe di densità
La correlazione trovata da Auger indica che gli AGN sono potenziali sorgenti di
UHECR, ma non costituisce una prova certa. Sappiamo infatti che la distribuzione
di materia nell’universo locale (entro 100 Mpc) è fortemente non uniforme, e che gli
AGN sono correlati con questa disomogeneità.
E’ quindi ragionevole cercare di capire se i dati che abbiamo costituiscano un’informazione sufficiente per determinare se il segnale di correlazione si può associare
in modo non ambiguo con gli AGN o se invece la correlazione esista con un altro
insieme di sorgenti con distribuzione simile a quella degli AGN.
Nel caso del catalogo VCV utilizzato nella ricerca di correlazione in Auger, si
utilizza il metodo descritto nel paragrafo 5.1.1, che ha come punto di partenza la
probabilità p vista come frazione del cielo accessibile all’osservazione da Auger, coperta da finestre circolari di una certa ampiezza centrate sulle posizioni degli AGN.
Questo è possibile poichè, nel caso degli AGN, la frazione di cielo coperta non
riempie la maggior parte del cielo; se per esempio si volesse studiare la correlazione
con le galassie normali, che sono molto più numerose, questo metodo non sarebbe
direttamente applicabile.
Una tecnica alternativa consiste nella costruzione, da un catalogo di sorgenti
discreto, di una mappa continua di probabilità delle direzioni di arrivo dei raggi
cosmici oltre una certa energia.
La mappa viene costruita a partire dalle posizioni degli oggetti specificate nel
catalogo, attraverso la sovrapposizione di distribuzioni gaussiane di larghezza fissata
σ (una scala angolare di alcuni gradi riferita alla deflessione tipica attesa per i raggi
cosmici).
Il fattore peso tiene conto della funzione di selezione del catalogo φ(z), della
distanza di luminosità della sorgente dL (z) e dell’attenuazione del flusso dovuto
all’effetto GZK:
/+∞
1
w(z, Eth ) =
E −s dE,
(5.8)
4πd2L (z)φ(z)
Ei (z,Eth )
dove Ei (z, Eth ) è l’energia iniziale minima richiesta per un raggio cosmico a redshift
z per raggiungere la terra con energia maggiore di Eth .
Nessun catalogo di galassie è completo e quindi sono necessarie delle stime sulla
completezza del catalogo dagli effetti di selezione; la quantità rilevante da derivare
è la frazione di galassie realmente osservate ai vari redshift, detta appunto funzione
di selezione. Un modo conveniente per esprimerla è in termini della distribuzione
73
della luminosità delle galassie φ(L):
φ(z) =
)∞
dLφ(L)
Lmin(z)
)∞
dLφ(L)
0
,
(5.9)
dove Lmin(z) è l’intensità minima rivelata in funzione del redshift.
La probabilità di osservare un evento da una particolare direzione nel cielo è proporzionale alla corrispondente densità nella mappa; per quantificare la correlazione
tra un set di dati e una data mappa si costruisce quindi la log-likelihood media per
evento:
N
1 >
log L =
log(p(li , bi ))
(5.10)
N i=1
dove N è il numero di eventi nel set di dati e p(li , bi ) è il valore della densità (ed è
quindi indice della probabilità di correlazione) nella direzione (li , bi ).
Generando dei sets di dati simulati distribuiti secondo le densità delle diverse
mappe con lo stesso numero di eventi presenti nei dati e confrontando i valori di L
per i dati con i valori attesi per i diversi scenari è possibile discriminare tra i vari
scenari.
In particolare si possono simulare eventi provenienti da una distribuzione isotropa
di sorgenti; a questo punto, utilizzando le varie mappe costruite con il procedimento
spiegato sopra, si possono calcolare le densità delle mappe stesse in direzione di ogni
evento, ottenendo quindi un insieme di valori per L. Si procede quindi confrontando
i valori di L per le simulazioni con il valore di L dei dati; il fatto che non sia stata
trovata compatibilità tra questi valori indica quindi che molti degli eventi simulati
cadono in regioni di bassa densità mentre molti degli eventi reali rientrano in regioni
ad alta densità, confermando quindi l’ipotesi di anisotropia delle direzioni di arrivo.
E’ possibile ripetere lo stesso procedimento con simulazioni di eventi provenienti
da distribuzioni che ricalcano le mappe di densità costruite sui diversi cataloghi; in
questo modo si possono distinguere i diversi modelli di distribuzione delle sorgenti
di UHECR.
5.2
Discussione sui risultati di Auger
Il fatto che le direzioni di arrivo degli eventi più energetici siano correlate con
le posizioni degli AGN non implica direttamente che questi siano le reali sorgenti
dei raggi cosmici; infatti si potrebbe avere che la distribuzione stessa deli AGN sia
correlata con la distribuzione di altre potenziali sorgenti, come per esempio i Gamma
Ray Bursts.
Se la statistica fosse maggiore, si potrebbero immaginare dei metodi diretti per
l’identificazione di sorgenti, ma avendo, a energie cosı̀ alte, uno o al più due eventi
che sembrano provenire dalla stessa sorgente, si può solo utilizzare la distribuzione
74
Confronto tra log L per evento in diversi intervalli di energia tra i dati e gli eventi
simulati (in blu i valori relativi ai dati simulati provenienti da una distribuzione isotropa,
in rosso i valori relativi ai dati simulati provenienti da una distribuzione anisotropa, in
particolare una distribuzione che ricalca quella degli AGN del catalogo VCV con una
finestra angolare di 2° da ogni AGN). I dati sono compatibili con una distribuzione che
segue quella degli AGN ad alte energie con una transizione verso una distribuzione isotropa
a energie più basse. [32]
Figura 5.3:
globale nel cielo per analizzare le diverse ipotesi sulla natura delle sorgenti.
La correlazione osservata è consistente con l’ipotesi che i raggi cosmici con le
energie più alte che arrivano a terra siano prodotti in AGN relativamente vicini,
entro la distanza oltre cui l’effetto GZK non attenua il loro flusso in modo significativo. L’orizzonte GZK può essere definito come la distanza dalla terra entro cui
sono contenute le sorgenti che producono il 90% dei protoni che arrivano con energie
oltre una data soglia. Ipotizzando le sorgenti come uniformemente distribuite e con
uguale luminosità intrinseca in raggi cosmici, l’orizzonte è circa 90 Mpc per protoni
che arrivano con energie oltre 80 EeV e circa 200 Mpc per energie oltre 60 EeV.
Il valore minimo della probabilità che gli eventi giungano da una distribuzione
isotropa corrisponde a correlazioni con AGN a distanze minori di 71 Mpc, per raggi
cosmici con energie oltre 57 EeV; si trovano comunque valori molto piccoli per la
probabilità in un intervallo di distanze che va da 50 a 100 Mpc.
Ci aspettiamo che la distanza massima Dmax degli AGN sia confrontabile con la
scala dell’orizzonte, ma la relazione tra queste due quantità può essere influenzata
da alcuni fattori. Una correlazione accidentale con un AGN vicino diverso dalla vera
sorgente può indurre degli errori nel valore di Dmax ; a questo si deve aggiungere il
fatto che l’incompletezza del catalogo VCV impedisce l’esplorazione oltre 100 Mpc.
Inoltre la stima della scala dell’orizzonte dipende anche da quanto la distribuzione
delle sorgenti sia lontana dall’essere unforme (una grande densità locale di sorgenti
potrebbe ridurre la distanza dell’orizzonte) e anche dalla distribuzione delle lumi-
75
nosità intrinseche.
La scala angolare della correlazione è consistente con la deflessione che ci si
aspetta dal campo magnetico galattico sui protoni; un raggio cosmico con carica Ze
! viene deflesso di un angolo
che attraversa una distanza D in un campo magnetico B
δ dato da:
; D
;
;/
;
!
60EeV ;; d!x
B ;;
∼
δ = 2.7
×
.
(5.11)
E/Z ;; kpc 3µG ;;
0
Se si prende il campo magnetico galattico dell’intensita di qualche µG con una scala
dell’ordine di ∼ 1 kpc, ci si aspetta una deflessione di alcuni gradi per protoni con
E > 60 EeV.
La scala angolare della correlazione osservata implica inoltre che i campi magnetici intergalattici presenti lungo la linea di vista delle sorgenti non possano deviare
le traiettorie dei raggi cosmici per più di qualche grado. Possono verificarsi degli
errori nella determinazione della scala angolare della deflessione; non è detto che
l’AGN più vicino alla direzione di arrivo di un raggio cosmico ne sia la sorgente.
Questo fattore può quindi implicare una sottostima della deflessione; d’altra parte,
l’AGN correlato ad un particolare evento potrebbe essere più lontano dalla direzione
di arrivo, e questo porterebbe ad una sovrastima dell’angolo di deflessione.
I siti di accelerazione nelle galassie attive che sono in correlazione con eventi oltre
57 EeV sono sorgenti candidate di raggi cosmici di alte energie, ma con la presente
statistica non possono essere esclusi altri possibili candidati.
Le correlazioni osservate escludono modelli che attribuiscono l’origine dei raggi cosmici a oggetti compatti nella nostra galassia, come stelle di neutroni, pulsars e buchi
neri, e a gamma ray bursts.
La distribuzione di materia nell’universo a grande scala, rappresentata dalle
galassie normali, è molto simile alla distribuzione degli AGN più vicini. Quindi
al momento non possono essere esclusi siti di accelerazione in galassie normali nè in
oggetti compatti extragalattici, in resti di quasar o in gamma ray bursts extragalattici.
Gli AGN vengono considerati da tempo dei possibili siti di accelerazione di raggi cosmici, e sono stati proposti diversi meccanismi che sfruttano differenti regioni
(dalle zone centrali ai getti e ai radio lobi) di questi oggetti per l’accelerazione.
AGN con radio lobes prominenti sono rari e non seguono la distribuzione spaziale
degli AGN in correlazione; l’unica eccezione è Cen A, a soli 3.4 Mpc, che ha due
eventi in correlazione e altri nelle vicinanze dell’estensione del lobo radio lungo il
piano galattico.
L’aumento della statistica contribuirà alla distinzione tra le due diverse ipotesi
degli AGN come sorgenti di raggi cosmici o indicatori delle sorgenti; se i dati futuri
eleggeranno gli AGN come ospiti degli acceleratori di raggi cosmici, il tipo di AGN
76
Mappa degli eventi UHECR (cerchi rossi) e AGN BAT entro 100 Mpc (cerchi
blu) in coordinate supergalattiche.
Figura 5.4:
selezionato aiuterà a distinguere tra i diversi meccanismi di accelerazione proposti.
5.3
5.3.1
Cataloghi alternativi
Swift BAT AGN Catalog
La correlazione degli eventi misurati da Auger con le sorgenti extragalattiche
è basata sul catalogo VCV, che risulta dall’insieme di diverse campagne di osservazione e contiene tutti i nuclei attivi e i quasars esistenti in letteratura, che sono
stati osservati nella banda ottica.
Nel lavoro di George et al. [34] si studia la correlazione delle direzioni di arrivo
degli UHECR di Auger con la posizione degli AGN presi dal catalogo Swift BAT
dei nuclei galattici attivi che emettono radiazione X; infatti i cataloghi selezionati
dal punto di vista ottico difficilmente includono i nuclei oscurati degli AGN.
Essendo le osservazioni nell’X duro meno sensibili all’oscuramento, possono dare
informazioni più precise sull’accrescimento e sulla luminosità intrinseca di un AGN.
Entro il campo di vista di Auger a distanze minori di 100 Mpc il catalogo VCV
contiene 410 oggetti, mentre le sorgenti catalogate da Swift con le stesse caratteristiche sono 57 e 6 di queste non sono presenti in VCV.
Nel lavoro citato sopra sono state inizialmente confrontate le posizioni degli AGN
con le direzioni di arrivo degli UHECR; successivamente le posizioni sono state pesate con il prodotto del flusso X per la relativa esposizione di Auger.
Restringendo il catalogo BAT alle zone in cui risulta completo e a quelle in
cui l’esposizione di Auger è diversa da zero rimangono 138 AGN e 19 UHECR; con
questa lista, la probabilità di avere correlazione è del 50%. La probabilità raggiunge
il 98% dopo aver pesato le coordinate degli AGN con il flusso X della sorgente e con
77
la relativa esposizione di Auger.
Restringendo ancora il catalogo alle 57 sorgenti con distanze minori di 57 Mpc
si trova una probabilità non pesata dell’84%; il valore pesato sul flusso non varia,
e questo può indicare il fatto che la correlazione è dominata da sorgenti vicine e
molto luminose. Con lo stesso taglio nel catalogo VCV George et al. ottengono una
correlazione del 55%.
Sono stati fatti dei tests analoghi sulla dipendenza della probabilità dalla luminosità delle sorgenti ed è stato osservato che, considerando l’intero catalogo, la
correlazione è minore per le sorgenti più luminose che per quelle più deboli; è possibile infatti che la radiazione che circonda gli AGN interferisca con la propagazione
degli UHECR. Al contrario, restringendosi a distanze minori di 100 Mpc sono le
sorgenti più luminose a correlare meglio. Questi risultati implicherebbero che il flusso dei raggi cosmici sia collegato alla luminosità degli AGN e che le lunghezze di
propagazione su scale di 100 Mpc inteferiscano con questo effetto.
La correlazione trovata con il catalogo BAT con le direzioni degli UHECR è più
alta di quella trovata con il catalogo VCV dagli stessi autori; da questa sola informazione, si potrebbe ipotizzare che sia un altro tipo di sorgenti con una distribuzione
locale simile a quella degli AGN ad essere responsabile dell’accelerazione degli UHECR. Ma è stato visto anche che pesando le coordinate degli AGN con il flusso X
o selezionando le sorgenti vicine più luminose, la correlazione aumenta; quindi una
classe alternativa di sorgenti responsabili dell’accelerazione dovrebbe ricalcare sia la
distribuzione spaziale locale che la distribuzione delle luminosità degli AGN.
Se gli AGN sono identificati con le sorgenti di UHECR, l’altro risultato importante di questo lavoro è la diminuzione della correlazione a distanze dell’ordine di
100 Mpc, oltre cui l’effetto GZK sopprime il flusso di raggi cosmici.
5.3.2
Correzioni al catalogo VCV
Nell’analisi originaria di Auger, senza tagli sul piano galattico, sono presenti 27
UHECR oltre 57 EeV, 20 dei quali sono in correlazione con una galassia del catalogo
VCV più vicina di z = 0.018; i 20 eventi sono correlati con 21 galassie VCV.
Nel lavoro di Zaw, Farrar & Greene [36] sono stati analizzati gli spettri di questi
oggetti e ne è stata data una classificazione alternativa, basata sui diagrammi diagnostici BPT (Baldwin et al, 1981) che utilizzano dei criteri legati all’intensità di
alcune righe proibite negli spettri di emissione in cui siano presenti righe ‘strette’.
Utilizzando certi criteri si possono quindi differenziare le Seyfert da regioni di emissione nucleare a bassa ionizzazione (LINERs) che non mostrano segni di attività
come gli AGN; infatti l’emissione di righe ‘strette’ può essere anche indice di formazione stellare.
Con questi criteri, 14 delle 21 galassie VCV, correlate con 14 UHECR, risultano
essere AGN.
78
La luminosità bolometrica (Appendice D) degli AGN correlati rappresenta un
test per le teorie sull’accelerazione di UHECR.
Sia R la dimensione caratteristica della regione accelerante nel sistema di riferimento del jet, con un campo magnetico di intensità B. Affinchè la turbolenza acceleri
un raggio cosmico ad una certa energia, la regione accelerante deve confinare il raggio comico stesso, cioè il raggio di Larmor della particella (0.1MpcE20 /ZBµG ) deve
essere minore di R:
RB > 3 × 1017 Γ−1 E20 G cm,
(5.12)
dove Γ è il fattore di Lorentz del jet.
La luminosità di Poynting del jet è data da L ∼ 16 cΓ4 B 2 R2 ; questo flusso di
energia è alimentato proprio dalla rimozione di momento angolare lungo l’asse perpedicolare al disco di accrescimento del buco nero supermassivo al centro dell’AGN,
e rappresenta un’importante caratteristica del processo di accelerazione.
In questo lavoro si pone infatti come limite per l’accelerazione di un raggio cosmico di E ≡ E20 1020 eV una luminosità bolometrica della sorgente superiore a quella
2
di Poynting: Lbol > 1045 Γ2 E20
erg/s.
Per definizione, la luminosità bolometrica di un oggetto è quella che si otterrebbe
raccogliendo l’emissione in tutte le lunghezze d’onda; in questo lavoro tale quantità
è stata calcolata utilizzando dei fattori di conversione tra, per esempio, la luminosità
X e quella bolometrica, o riscalando il flusso misurato in alcune particolari lunghezze
d’onda o di alcune righe di emissione.
Per ogni coppia di AGN-UHECR è stato quindi calcolato il parametro λbol ≡
−2
Lbol 10−45 E20
, e si può vedere che solo in un caso si ha λbol > 1, mentre in altri
casi questo parametro resta di poco inferiore al limite; nel modello degli AGN flares
tutto ciò sarebbe plausibile.
Secondo questo modello infatti gli UHECR sarebbero accelerati in lampi relativamente brevi (della durata di un mese o meno), durante i quali il limite richiesto
per la luminosità è superato, mentre al di fuori di questi periodi si osserverebbe
semplicemente un AGN in accrescimento. Questi brillamenti avrebbero inizio nel
momento in cui una instabilità del disco di accrescimento o la distruzione di una
stella a causa delle forze di marea riscalda il disco stesso.
Un altro aspetto interessante della correlazione osservata da Auger è la mancanza di UHECR dall’ammasso di Virgo; ciò può apparire strano, a causa della sua
vicinanza e del grande numero di galassie VCV in Virgo. In questo lavoro sono state
analizzate 30 galassie VCV che si trovano nell’ammasso entro un certo redshift e
entro una certa distanza dal centro; le loro luminosità bolometriche risultano essere
sistematicamente più basse rispetto a quelle degli AGN correlati con gli UHECR
(che vanno da 5 × 1042 a 1 × 1046 erg/s).
Se gli UHECR sono preferibilmente accelerati da AGN oltre la soglia di luminosità
considerata sopra, ci si potrebbe aspettare una correlazione ridotta tra UHECR osservati da esperimenti nell’emisfero nord e galassie VCV rispetto a quella vista da
Auger nell’emisfero sud; questo proprio perchè una sostanziale frazione degli AGN
79
nell’emisfero nord sono LLAGN (Low Luminosity AGN), a causa della sensibilità
delle osservazioni spettroscopiche di Palomar delle galassie vicine.
HiRes ha recentemente ripetuto le analisi di correlazione fatte da Auger trovando
2 eventi in correlazione dei 13 eventi osservati.
Una luminosità bolometrica minima richiesta per le galassie che accelerano UHECR potrebbe spiegare sia l’assenza di UHECR correlati con AGN nell’ammasso di
Virgo sia la relativamente bassa correlazione riportata da HiRes, poichè esisterebbe
una propozione maggiore di AGN a bassa luminosità nel catalogo VCV nel campo
di vista di HiRes rispetto al campo di vista di Auger.
80
Capitolo 6
Risultati
Gli esperimenti Auger e HiRes misurano lo spettro dei raggi cosmici ad alte
energie, mostrando l’esistenza di una attenuazione del flusso a energie intorno a
1019.5 eV.
Il cut-off osservato in entrambi gli esperimenti può essere giustificato con un
argomento che riguarda le caratteristiche dell’interazione tra i protoni e la radiazione
cosmica di fondo; l’effetto GZK prevede infatti una soppressione del flusso di raggi
cosmici prodotti ad una certa distanza dall’osservatore a causa della reazione di
fotoproduzione di pioni (come spiegato nel capitolo 3).
L’osservazione di questa caratteristica dello spettro prevista nell’ambito delle
teorie bottom-up permette di mettere in secondo piano le teorie top-down per la
produzione di raggi cosmici, introdotte per spiegare dal punto di vista teorico l’osservazione di un eccesso nel flusso misurato dall’esperimento AGASA.
Nell’ambito di queste teorie si ipotizza la provenienza dei raggi cosmici da sorgenti astrofisiche galattiche e extragalattiche con opportune dimensioni della regione
accelerante e opportuni valori del campo magnetico.
In aggiunta alla misura del flusso, nell’esperimento Auger, come spiegato nel
capitolo precedente, è stato possibile confrontare le direzioni di arrivo dei raggi cosmici con le posizioni dei nuclei galattici attivi trovando una correlazione positiva.
Avendo quindi delle informazioni sulle possibili sorgenti, è interessante calcolare
il flusso di raggi cosmici proveniente da questi oggetti. A questo calcolo seguirà
quindi il confronto con il flusso misurato da Auger.
Questo lavoro di Tesi, grazie al confronto tra i due spettri, rappresenta un punto di collegamento tra le evidenze osservative che offre Auger; in questo capitolo
si analizza il confronto tra lo spettro sperimentale misurato da Auger e lo spettro
teorico da noi calcolato. Si elencano inoltre i parametri che rientrano nei calcoli e le
variazioni alcuni di questi determinano sullo spettro teorico.
Riportiamo innanzi tutto delle informazioni sulla misura del flusso in Auger;
spieghiamo quindi il procedimento utilizzato per il calcolo del flusso teorico e discu-
81
Spettro misurato da HiRes-1 e HiRes-2 singolarmente e spettro misurato dal
rivelatore di superficie di Auger [39].
Figura 6.1:
tiamo infine le scelte fatte per i parametri utilizzati nei calcoli. Rimandiamo infine
alla parte sulle Conclusioni per una discussione completa sui parametri utilizzati nei
calcoli e sulle conseguenze che la scelta di questi ha comportato sul confronto con il
flusso sperimentale; discutiamo inoltre nelle Conclusioni gli obbiettivi raggiunti con
questo lavoro di Tesi e i possibili sviluppi di questo lavoro.
6.1
Spettro di Auger
Lo sviluppo longitudinale dello sciame in atmosfera viene misurato utilizzando
i rivelatori di fluorescenza; la luce prodotta viene rivelata come una serie di pixels
illuminati in una o più camere. La posizione di questi pixels e il tempo di arrivo
della luce determinano la direzione dello sciame.
Il segnale, dopo le correzioni per l’attenuazione dovuta allo scattering Rayleigh
e allo scattering degli aerosol, è proporzionale al numero di fotoni di fluorescenza
emessi nel campo di vista del pixel; si deve inoltre tenere conto della contaminazione
data dalla luce di fluorescenza prodotta ad angoli vicini all’asse dello sciame e che
può essere scatterata verso i pixels.
Utilizzando la funzione di Gaisser-Hillas (equazione 4.22) si può quindi ricostruire
il profilo dello sciame che dà una misura dell’energia dell’EAS rilasciata in atmosfera;
per derivare l’energia del primario viene fatta una stima dell’energia trasportata da
muoni e neutrini basandosi sulle assunzioni circa la massa del raggio cosmico primario. L’incertezza sistematica è del 4%.
E’ necessario inoltre stimare gli errori sistematici nella misura dell’energia dell’FD. Le incertezze maggiori si trovano nel prodotto di fluorescenza (14%), nella
82
calibrazione assoluta dei telescopi (10%) e nel metodo di ricostruzione (10%); gli
errori proventienti dagli aerosols atmosferici, la dipendenza dello spettro di fluorescenza dalla temperatura e dall’umidità arrivano entrambi al 5%.
Considerando quindi tutti i contributi, si trova un errore sistematico del 22%
nella determinazione dell’energia.
Lo spettro in energia basato su 20000 eventi è mostrato in figura 6.2; è fittato
da una funzione con energia di soppressione a 4 × 1019 eV, definita come l’energia in
corrispondenza della quale il flusso diminuisce del 50% rispetto alla legge di potenza
estrapolata.
Per esaminare la forma spettrale alle energie più alte, lo spettro è stato fittato con
una funzione a legge di potenza (J ∝ E −γ ) tra 4 × 1018 eV e 4 × 1019 eV, ottenendo
γ = 2.69 ± 0.02(stat)±0.06(sist), dove l’incertezza sistematica viene dalla curva di
calibrazione. L’indice spettrale oltre 4 × 1019 eV è γ = 4.2 ± 0.4(stat)±0.06(sist); è
stato inoltre utilizzato un metodo indipendente dall’indice γ per rigettare l’ipotesi
di singola legge di potenza oltre 4 × 1018 eV con una significatività maggiore di 6
deviazioni standard.
In figura 6.2 si può vedere la differenza rispetto ad un flusso assunto di E −2.69 ; i
dati di HiRes I mostrano uno spettro più soft dove l’indice dello spettro di Auger è
2.69, mentre la posizione della soppressione è in accordo tra i due esperimenti, entro
l’incertezza sistematica.
Il fatto che sia stata rigettata l’ipotesi che lo spettro di raggi cosmici continui
con una pendenza costante oltre 4 × 1019 eV, con una significatività di 6 deviazioni
standard è un risultato molto importante, se considerato insieme al fatto che la
ricerca di correlazione fatta da Auger con sorgenti extragalattiche ha dato esiti
positivi.
Questi risultati presi insieme possono essere infatti interpretati come la verifica
della previsione GZK riguardo ai motivi della soppressione del flusso.
6.2
Spettro teorico
I dati di Auger mostrano evidenza di un’anisotropia nelle direzioni di arrivo dei
raggi cosmici alle energie più alte; nel capitolo precedente sono state riportate alcune
informazioni sul confronto tra le direzioni degli eventi e le posizioni degli AGN e la
correlazione positiva annunciata da Auger.
Avendo a disposizione in letteratura le luminosità delle sorgenti trovate in correlazione è possibile calcolare il flusso di raggi cosmici da esse provenienti, ipotizzando
uno spettro di iniezione alla sorgente a legge di potenza; lo spettro in energia che
ne risulta rappresenta il punto di collegamento tra le informazioni fornite dalla correlazione trovata da Auger e lo spettro misurato.
Nel calcolo dello spettro teorico entrano diversi parametri; al variare di questi
è possibile riprodurre lo spettro misurato, ottenendo quindi delle informazioni sugli
83
Parte superiore: Flusso differenziale J in funzione dell’energia, con le incertezze
statistiche. Parte inferiore: differenza tra i dati di Auger e HiRes I confrontati con uno
spettro con un indice 2.69 [42].
Figura 6.2:
oggetti candidati a sorgenti di raggi cosmici.
Dato l’esiguo numero delle sorgenti correlate e data la bassa statistica delle misure di Auger non è possibile trarre delle conclusioni sulla classe di sorgenti che
possono accelerare raggi cosmici; si può comunque vedere come varia lo spettro calcolato ad alte energie a seconda delle sorgenti che si includono nel calcolo.
Nei paragrafi che seguono si riportano i procedimenti per il calcolo del flusso
teorico; questo sarà la somma del flusso proveniente dalle sorgenti trovate in correlazione e del flusso proveniente da una distribuzione uniforme di sorgenti per redshift
oltre 0.017.
In generale i cataloghi di AGN risultano incompleti sul piano galattico, dove
l’estinzione dovuta alla polvere nella Galassia riduce la sensibilità delle osservazioni;
in particolare il catalogo VCV risulta dalla somma di varie campagne di osservazione,
per cui alcune zone del cielo risultano meno esplorate di altre. Il catalogo si può
comunque considerare completo ai fini della ricerca delle correlazioni entro 100 Mpc.
All’aumentare della distanza le sorgenti rivelate nelle varie campagne di osservazione saranno solo le più luminose, quindi il catalogo risulta sempre più disomogeneo.
Al contrario, se fossimo in grado di rivelare tutte le sorgenti, per distanze maggiori di 100 Mpc ci possiamo aspettare di osservare un universo con una distribuzione
uniforme di sorgenti; poichè non esiste un catalogo completo da questo punto di
84
vista, utilizziamo da redshift 0.018 in poi una distribuzione uniforme di sorgenti.
Lo spettro totale sarà quindi la somma dei due contributi descritti sopra; da
notare che in questo procedimento avremo che ad alte energie contribuirà solo la
componente discreta, in quanto quella della distribuzione uniforme andrà a zero per
l’effetto combinato della soppressione del flusso data dal GZK e dell’energia massima
a cui possono essere accelerate particelle utilizzata nel calcolo. A energie più basse
si avranno invece entrambi i contributi.
6.2.1
Calcolo del flusso da sorgenti discrete
Per calcolare lo spettro di emissione delle sorgenti correlate con gli eventi di Auger
dobbiamo calcolare il flusso di ogni singola sorgente con la propria luminosità; come
già visto nel capitolo 3 il flusso da una singola sorgente è dato da:
J(E, z) =
1 Qinj (Eg (E, z)) dEg (E, z)
.
(4π)2 (1 + z)(R(t0 )r)2
dE
(6.1)
R(t0 )r = R(t)r(1 + z);
(6.2)
dove R(t0 )r è dato da
rR(t0 ) = c
/0
z
avendo preso
!
dt
dz
c
dt
dz (1 + z) =
dz
H0
"−1
/zg
0
dz
2
(1 + z)3 Ωm + ΩΛ
2
= −H0 (1 + z) (1 + z)3 Ωm + ΩΛ .
(6.3)
(6.4)
Per avere lo spettro totale delle sorgenti in questione basterà quindi sommare ogni
singolo contributo.
Per quanto riguarda l’espressione dello spettro di iniezione, si avrà:
3
#
$−γ
$−γ
#
E
E
Q0 Emin
= L0E(γ−2)
E ≤ Emax
2
Emin
Qinj (E) =
(6.5)
min
0
E > Emax
e L0 è proprio la luminosità assoluta della sorgente considerata; nel caso della distribuzione uniforme di sorgenti si utilizzerà la stessa espressione per l’iniezione, con
valori di L0 determinati come spiegato nel prossimo paragrafo.
Nel catalogo VCV vengono fornite per ogni oggetto le magnitudini nelle bande B,
U, V e la magnitudine assoluta M , che si riferisce alla magnitudine apparente nella
banda B. Dalla magnitudine assoluta si può ricavare la luminosità di ogni oggetto
come spiegato in Appendice D.1.
85
Costruzione della lista di sorgenti
Il segnale di correlazione annunciato da Auger si basa sul fatto che dei 27 eventi
registrati da Auger dal 1 gennaio 2004 al 31 agosto 2007 con energia oltre 57 EeV
si hanno 20 eventi che correlano entro 3.2° con AGN con redshift z ≤ 0.017; questa
ricerca è stata fatta utilizzando la 12a edizione del catalogo di nuclei attivi e quasars
(catalogo VCV, [6].
Ciò significa che, all’interno delle finestre circolari di 3.2° centrate sulla direzione
di arrivo dell’evento, per 20 dei 27 eventi più energetici sono stati trovati degli oggetti
che nel catalogo VCV vengono calssificati come BL Lac, AGN o Quasars.
Catalogo VCV. Ai fini del calcolo del flusso teorico da sorgenti extragalattiche,
è stato quindi necessario selezionare una lista di sorgenti dal catalogo VCV; ciò è
stato fatto prendendo l’intero catalogo VCV contenente 21737 galassie attive, 1122
BL Lac e 85221 quasars e selezionando l’oggetto (o gli oggetti) con z ≤ 0.017 e entro
3.2° dalla direzione dell’evento considerato.
Quello che abbiamo ottenuto è una lista di 30 sorgenti; in alcuni casi si può avere
infatti che un evento ha più di una sorgente entro 3.2° dalla sua direzione.
Questo significa che, se ho un numero n di sorgenti entro l’apertura angolare
prescelta, n − 1 delle correlazioni che ne risultano saranno casuali e quindi solo una
di queste sorgenti dovrà rientrare nel calcolo del flusso.
Dalla lista di sorgenti non è possibile distinguere dei criteri che favoriscano la
scelta di una sorgente all’interno della finestra angolare piuttosto che un’altra, cioè
dalle caratteristiche degli AGN non si deducono dei motivi per preferire un AGN ad
un altro come sito di provenienza dei raggi cosmici.
Come criterio di scelta si può quindi utilizzare un semplice fatto legato alla
potenza della sorgente, prendendo quindi l’oggetto con luminosità più alta; si può
anche pensare di prendere la sorgente la cui posizione abbia minore distanza angolare
dall’evento corrispondente, pensando quindi che il campo magnetico galattico non
sia in grado di deflettere significativamente la direzione dell’evento di UHECR.
Dall’unica lista iniziale con 30 sorgenti sono state quindi costruite due liste;
per gli eventi con più di un oggetto entro 3.2° sono stati scelti in una prima lista,
gli oggetti più luminosi (Lista 1), nell’altra gli oggetti più vicini (Lista 2). Le
magnitudini riportate nel catalogo per le sorgenti in correlazione vanno da un minimo
di -14.4 (Centaurus A) a -21.9, che corrispondono rispettivamente a luminosità di
circa 1041 erg/s e 1044 erg/s.
In figura 6.3 si può vedere un confronto tra i flussi teorici nelle due liste; si può
notare che ad alte energie conta di più il contributo della lista contenente le sorgenti
con distanza angolare minore dall’evento; ciò è dovuto al fatto che in generale le
sorgenti più luminose presenti nell’altra lista sono quelle più lontane e quindi danno
un maggiore contributo al flusso a basse energie.
86
E3 J(E) [eV2 m-2 s-1]
1018
1017
Lista 1
Lista 2
1017
1018
1019
1020
E [eV]
Confronto tra i flussi teorici dagli AGN di Lista 1 e Lista 2 dal catalogo VCV,
calcolati con le luminosità assolute proprie di ogni sorgente e con iniezione γ = 2.7, energia
massima Emax = 1021 eV, evoluzione delle sorgenti m = 0.
Figura 6.3:
In figura 6.4 si può vedere il contributo delle sorgenti della Lista 1 suddivise
in tre intervalli di redshift; il contributo delle sorgenti nell’intervallo più vicino non
mostra attenuazione del flusso. Inoltre si può vedere che il contributo maggiore al
flusso viene dato dalle sorgenti oltre redshift 0.012, sia perchè in questo intervallo
si trovano la maggior parte delle sorgenti in correlazione, sia perchè queste sono le
sorgenti più luminose.
Correzioni al catalogo VCV. Nel lavoro di Zaw et al. [36] sono stati analizzati gli
spettri degli AGN appartenenti al catalogo VCV trovati in correlazione da Auger;
secondo i criteri qui utilizzati è stato trovato che soltanto 15 delle sorgenti in correlazione con gli UHECR di Auger risultano essere AGN, mentre le altre non mostrano
segni di attività. Le luminosità stimate per questi oggetti sono 5 × 1042 ÷ 1 × 1046
erg/s.
Procediamo quindi anche in questo caso alla compilazione di due diverse liste;
come prima, per gli eventi con più di un oggetto entro 3.2° sono stati scelti in una
prima lista, gli oggetti più luminosi (Lista 1b), nell’altra gli oggetti più vicini (Lista
2b). In questo caso le due liste differiscono però per due soli oggetti di luminosità
simile e, come si può vedere in figura 6.5, ciò non influisce sul flusso in modo significativo.
Catalogo Swift BAT. Come riportato nel capitolo 5, sappiamo che da osservazioni
nella banda X possiamo avere informazioni più precise sull’accrescimento e la luminosità intrinseca di un AGN rispetto alle osservazioni nella banda ottica.
E’ utile quindi, con lo stesso procedimento applicato sul catalogo VCV, se-
87
E3 J(E) [eV2 m-2 s-1]
1024
0<z<0.003
0.003<z<0.012
0.012<z<0.018
1023
1022
1021
1020 17
10
1018
1019
1020
E [eV]
Confronto tra i flussi teorici dagli AGN della Lista 1, suddivisa in tre intervalli
di redshift, calcolati con le luminosità assolute proprie di ogni sorgente e con iniezione
γ = 2.1, energia massima Emax = 1021 eV, evoluzione delle sorgenti m = 0.
E3 J(E) [eV2 m-2 s-1]
Figura 6.4:
1019
Lista 1b
Lista 2b
1017
1018
1019
1020
E [eV]
Confronto tra i flussi teorici dagli AGN di Lista 1b e Lista 2b dal catalogo
VCV corretto, calcolati con le luminosità bolometriche proprie di ogni sorgente e con
iniezione γ = 2.7, energia massima Emax = 1021 eV, evoluzione delle sorgenti m = 0.
Figura 6.5:
88
sorgenti X
E3 J(E) [eV2 m-2 s-1]
1019
1018
1017
1018
1019
1020
E [eV]
Flusso teorico dagli AGN nella Lista X, calcolato con le luminosità nella
banda X proprie di ogni sorgente e con iniezione γ = 2.7, energia massima Emax = 1021
eV, evoluzione delle sorgenti m = 0.
Figura 6.6:
lezionare dal catalogo in esame, le sorgenti entro 3.2° da ogni evento di Auger per
cui sia stata trovata una correlazione positiva.
Non è stato possibile utilizzare il catalogo completo cui si fa riferimento in [34]
perchè non ancora pubblicato, ma è stato applicato il procedimento sopra descritto al catalogo parziale riferito ai primi 9 mesi di raccolta dati della campagna di
osservazione di nuclei galattici attivi di Swift BAT nella banda 14 ÷ 195 keV, che
raccoglie 154 AGN [35].
Sono stati trovati solo 5 AGN di questo catalogo che si trovano entro 3.2° rispetto agli eventi di Auger e il flusso è riportato in figura 6.6; le luminosità di questi 5
oggetti vanno da circa 1042 erg/s a 3 × 1045 erg/s.
6.2.2
Calcolo del flusso da distribuzione uniforme
Calcoliamo il flusso da distribuzione uniforme di sorgenti come spiegato nel
capitolo 3:
c
Jtot (E) =
4π
z/max
dz
0
(1 + z)−1 Q̃(Eg (E, z), z) dEg (E, z)
2
;
dE
H0 (1 + z)3 Ωm + ΩΛ
(6.6)
come prima, prendiamo Q̃ = n0 Q, e n0 è la densità di sorgenti per unità di volume.
Abbiamo inoltre preso zmax come soluzione di Eg (E, z) = Emax .
Nel caso di una distribuzione uniforme di sorgenti non si definisce una luminosità
per ogni sorgente ma si prende un valore della luminosità per unità di volume.
89
E3 J(E) [eV2 m-2 s-1]
1025
Auger
γ=2.7
2.4
2.1
1024
1023
1022 17
10
1018
1019
1020
1021
E [eV]
Spettro da distribuzione uniforme, calcolato per diversi parametri di iniezione
γ, a confronto con lo spettro misurato da Auger. Nei calcoli è stato preso Emax = 1021
eV, m = 0.
Figura 6.7:
Utilizziamo un valore della densità di sorgenti pari a n0 = 10−5 Mpc−3 ; questo
valore è suggerito dall’osservazione del clustering a piccoli angoli nelle direzioni di
arrivo dei raggi cosmici con energie oltre 4 × 1019 eV in AGASA, che ha trovato
un certo numero di doppietti negli eventi; la densità delle sorgenti necessaria per
spiegare il numero di doppietti osservati sarebbe appunto n0 = (1÷4)×10−5 Mpc−3 ,
come riportato in [43]. Questo valore è inoltre in accordo con la densità stimata di
AGN nell’universo.
La quantità che si utilizza è quindi la luminosità per unità di volume: L0 = L0 n0 .
Calcolando i flussi teorici con diversi valori dell’indice γ e confrontandoli con i
dati di Auger (figura 6.7) si trovano i seguenti valori per le luminosità:
• L0 (γ = 2.7) = 8.48 × 1048 erg/s
• L0 (γ = 2.4) = 8.40 × 1045 erg/s
• L0 (γ = 2.1) = 1.86 × 1043 erg/s
e dunque la luminosità per unità di volume sarà:
• L0 (γ = 2.7) = 8.48 × 1043 erg/(s Mpc3 )
• L0 (γ = 2.4) = 8.40 × 1040 erg/(s Mpc3 )
• L0 (γ = 2.1) = 1.86 × 1038 erg/(s Mpc3 )
90
1025
zmin=0
0.018
0.05
0.1
0.3
0.5
E3 J(E) [eV2 m-2 s-1]
1024
1023
1022
1021 17
10
1018
1019
1020
1021
E [eV]
Figura 6.8: Esempio di spettri da distribuzione uniforme
8.48 × 1048 erg/s, al variare del redshift minimo.
6.3
calcolati per γ = 2.7 e con L0 =
Parametri del flusso
I parametri che entrano nel calcolo dello spettro in energia sono:
• zmin , il redshift minimo a partire dal quale si utilizza una distribuzione uniforme di sorgenti;
• γ, lo spettro di iniezione alla sorgente;
• L0 , la luminosità in raggi cosmici delle distribuzioni di sorgenti;
• Emax , l’energia massima a cui possono essere accelerati raggi cosmici alla
sorgente;
• m, l’evoluzione cosmologica delle sorgenti.
Analizziamo nel dettaglio i parametri elencati, mostrando con delle figure come varia
lo spettro al variare di essi.
Redshift
Nel caso dell’utilizzo del catalogo VCV abbiamo visto che per redshift oltre
0.018 il catalogo non è completo; quindi il parametro zmin non potrà essere inferiore
a questo valore.
91
Spettro di iniezione
L’utilizzo di una funzione a legge di potenza per lo spettro di iniezione degli
UHECR è motivata dai modelli dell’accelerazione da shock; questi modelli prevedono
un esponente tipico γ ≈ 2.0 ÷ 2.2.
In figura 6.7 si può invece vedere che uno spettro di iniezione con γ = 2.7 si
avvicina molto meglio allo spettro misurato da Auger che non quello con γ = 2.1.
Finora abbiamo assunto che la distribuzione uniforme di sorgenti sia composta da
sorgenti con le stesse caratteristiche, ovvero la stessa luminosità e la stessa energia
massima a cui vengono accelerati i raggi cosmici alla sorgente.
Sappiamo però che l’energia di accelerazione di una certa sorgente dipende da
parametri che variano da sorgente a sorgente, come l’intensità del campo magnetico
e le dimensioni della regione accelerante; quindi ci si può aspettare che Emax sia
diversa a seconda della sorgente presa in esame.
E’ stato dimostrato che la sovrapposizione di spettri con iniezione 2.0 ÷ 2.2 di
singole sorgenti poste a diverse distanze e con diversi valori per Emax può produrre
uno spettro da distribuzione uniforme con un indice γ maggiore di quello che si
avrebbe nel caso di singola sorgente [44].
Nei calcoli abbiamo quindi utilizzato diversi valori dell’indice di iniezione γ per
la componente discreta e per quella uniforme.
Il valore di γ per la parte uniforme è, per i motivi detti sopra, maggiore di quello
preso per la parte discreta; infatti il contributo da distribuzione uniforme si estende
fino alle energie più basse e permette quindi di sommare i contributi delle sorgenti
fino a redshift molto alti.
Il risultato netto sarà quindi quello di avere un γ effettivo più alto di quello che
ci si può apettare dall’accelerazione di Fermi.
Nella parte dello spettro alle energie più alte, a causa delle perdite di energia
considerate, l’universo visibile è ristretto ad un raggio di circa 100 Mpc e quindi la
distribuzione di sorgenti non sarà uniforme; l’insieme di sorgenti discrete che stiamo
considerando contribuisce quindi ad un valore netto dello spettro di iniezione più
vicino all’esponente dello spettro del modello dell’accelerazione da shock.
Luminosità
Un altro importante parametro che fissa lo spettro atteso è la luminosità delle
sorgenti e, per la distribuzione uniforme, la densità delle stesse. La densità delle
sorgenti nella distribuzione uniforme si è assunta pari a n0 = 10−5 M pc−3 , che
corrisponde alla densita’ di AGN stimata fino ad alto redshift. Fissata la densità, si può stimare l’emissività come spiegato nel paragrafo precedente, trovando
L0 = 1038 ÷ 1043 erg/(sMpc3 ).
Nel caso delle sorgenti discrete il parametro che entra nella determinazione dello
spettro è la luminosità in raggi cosmici L0 . Nei cataloghi utilizzati si avevano a
disposizione le luminosità in fotoni per fissate bande dello spettro. In questo caso,
dunque, si è assunto la luminosità in protoni UHE proporzionale alla luminosità
92
E3 J(E) [eV2 m-2 s-1]
1018
1017 17
10
Emax=1020
eV
Emax=1021eV
22
Emax=10 eV
1018
1019
1020
1021
E [eV]
Confronto tra i flussi teorici dalla Lista 1 per diversi valori di Emax . Nei calcoli
sono stati presi γ = 2.7, m = 0.
Figura 6.9:
osservata in fotoni, determinando il coefficiente di proporzionalità dal confronto con
lo spettro di Auger, come si spiega nel paragrafo successivo.
In questo contesto e’ stata fatta un’ulteriore semplificazione assumendo che l’efficienza di conversione della potenza della sorgente in luminosità di raggi cosmici
sia la stessa per ogni sorgente da catalogo. In una situazione più realistica, questa
efficienza sarà diversa da sorgente a sorgente.
Energia massima
Il valore dell’energia massima a cui possono essere accelerati i raggi cosmici alla
sorgente influenza il flusso degli UHECR oltre ∼ 5 × 1019 eV, mentre il flusso a
energie più basse è indipendente da Emax , come si puo vedere sia nel caso delle
sorgenti discrete (6.9), che nel caso della distribuzione uniforme (6.10).
Da notare che, nel caso di un valore dell’energia massima pari a 1022 eV la
differenza con il caso di Emax = 1021 eV è data soltanto dal fatto che nel secondo
caso il flusso va a zero intorno a 7 × 1020 eV, ma la struttura del GZK prevale in
entrambi. Invece per energie massime minori, la soppressione del flusso sarà data
da una combinazione dell’energia massima scelta e dell’effetto GZK.
93
E3 J(E) [eV2 m-2 s-1]
1024
1023
1017
Emax=8x1019eV
1020
1021
1022
Auger
1018
1019
1020
1021
E [eV]
Confronto tra i flussi teorici da distribuzione uniforme per diversi valori di
Emax . Nei calcoli sono stati presi γ = 2.7, m = 0.
Figura 6.10:
Evoluzione cosmologica delle sorgenti
Nel capitolo 3 abbiamo visto come si modifica lo spettro di iniezione Qinj se si
assume un’evoluzione cosmologica delle sorgenti diversa da zero:
L0 → L0 (1 + z)m .
(6.7)
Questa modifica del flusso si può avere sia nel caso di sorgenti individuali che nel caso
di una distribuzione; in particolare, nel nostro caso l’evoluzione contribuirà ad una
variazione del flusso solo nel caso della distribuzione uniforme di sorgenti in quanto
le sorgenti discrete hanno redshift molto piccoli e la variazione della luminosità con
z non è rilevante.
6.4
Calcolo del flusso teorico totale
Tenendo conto dei parametri coinvolti nel calcolo del flusso di raggi cosmici dai
contributi delle due distribuzioni di sorgenti considerate, procediamo ora alla somma dei due contributi. Questa è stata fatta utilizzando il seguente procedimento, in
cui riportiamo i parametri utilizzati per la realizzazione dei grafici nelle figure 6.11,
6.13 e 6.14. Per quanto riguarda i grafici che seguono, discutiamo in seguito i diversi
valori di energia massima e di evoluzione cosmologica delle sorgenti utilizzati.
Nel calcolo del flusso totale (per le prime tre figure citate sopra) da entrambi i contributi è stato preso un valore dell’energia massima pari a 2 × 1020 eV e
l’evoluzione cosmologica delle sorgenti è stata presa sempre uguale a zero.
E’ stato calcolato il flusso da una distribuzione uniforme di sorgenti con zmin = 0
94
E3 J(E) [eV2 m-2 s-1]
Emax,uni=Emax,AGN=2x1020 eV
1024
Auger
somma
AGN Lista 1
distr.uniforme
1017
1018
1019
1020
E [eV]
Figura 6.11:
erg/(s
Somma dello spettro da distribuzione uniforme (γ = 2.6, L0 = 8.56 × 1042
e dello spettro delle sorgenti della Lista 1 (γ = 2.1, η = 1.36).
Mpc3 ))
e zmax = 4 e questo flusso è stato confrontato con il flusso misurato da Auger, trovando un certo valore per la luminosità per unità di volume.
Questo valore per la luminosità è stato dunque utilizzato per calcolare il flusso
da una distribuzione uniforme di sorgenti con zmin = 0.018 e zmax = 4:
c
J0.018 (E) =
4π
/4
0.018
dz
(1 + z)−1 Q̃(Eg (E, z), z) dEg (E, z)
2
,
dE
H0 (1 + z)3 Ωm + ΩΛ
(6.8)
dove in Q̃ ho la luminosità della distribuzione totale di sorgenti.
Il flusso totale Jtot sarà dunque il risultato della somma della componente uniforme fino a z = 0.018 e della componente discreta JAGN (che arriva fino a z = 0.001),
con un certo peso:
Jtot = J0.018 + ηJAGN ;
(6.9)
il fattore η si determina quindi confrontando la somma con i dati di Auger; il valore
trovato per la luminosità in protoni delle sorgenti discrete sarà allora dato da:
Lp,i = ηL0,i .
(6.10)
Gli esempi relativi ai vari cataloghi utilizzati sono rappresentati nelle figure che
seguono, con i valori trovati per il fattore di conversione η che, come detto precedentemente, viene preso uguale per ogni sorgente discreta.
Un primo commento da fare è relativo alla figura 6.12, il cui grafico è ottenuto con
il contributo della Lista 2 (le sorgenti in correlazione più luminose, come spiegato
95
E3 J(E) [eV2 m-2 s-1]
Emax,uni=Emax,AGN=2x1020 eV
1024
Auger
somma
AGN Lista 2
distr.uniforme
1017
1018
1019
1020
E [eV]
Figura 6.12:
erg/(s
Somma dello spettro da distribuzione uniforme (γ = 2.6, L0 = 8.56 × 1042
e dello spettro delle sorgenti della Lista 2 (γ = 2.1, η = 1.15).
Mpc3 ))
E3 J(E) [eV2 m-2 s-1]
Emax,uni=Emax,AGN=2x1020 eV
1024
Auger
somma
AGN Lista 1b
dist. uniforme
1017
1018
1019
1020
E [eV]
Somma dello spettro da distribuzione uniforme (γ = 2.6, L0 = 8.56 × 1042
erg/(s Mpc3 )) e dello spettro delle sorgenti della Lista 1b (γ = 2.1, η = 3.42 × 10−2 ).
Figura 6.13:
96
E3 J(E) [eV2 m-2 s-1]
Emax,uni=Emax,AGN=2x1020 eV
1024
Auger
sum
AGN Lista X
dist.uniforme
1017
1018
1019
1020
E [eV]
Figura 6.14:
erg/(s
Somma dello spettro da distribuzione uniforme (γ = 2.6, L0 = 8.56 × 1042
e dello spettro delle sorgenti della Lista X (γ = 2.1, η = 2.03 × 10−1 ).
Mpc3 ))
nel paragrafo relativo alla costruzione delle liste); come si può vedere, per i valori
di E 3 J(E) che ci interessano, le differenze osservate nel flusso delle sorgenti delle
due diverse liste (come si vede nella figura 6.3) non influiscono nel calcolo del flusso
totale. Nel seguito riportiamo quindi i risultati relativi alla Lista 1.
Osserviamo inoltre, nella figura 6.13, una risalita del flusso alle energie dove contribuisce soltanto la distribuzione discreta di sorgenti; per commentare tale struttura
dobbiamo premettere che tra le sorgenti trovate in correlazione con gli eventi più
energetici di UHECR ci sono due sorgenti molto vicine. Una di queste è proprio
Centaurus A (descritta nel capitolo 2), che si trova a redshift 0.001; l’altra è una
sorgente anch’essa molto vicina, avente redshift 0.002, denominata NGC 4945. Nel
calcolo del flusso avremo che Centaurus A dà un contributo doppio in quanto correla
con due eventi di UHECR registrati da Auger; questo equivale ad avere 3 sorgenti
molto vicine.
Queste 3 sorgenti sono presenti sia nella Lista 1 ottenuta dal catalogo VCV che
nella Lista 1b ottenuta dalle correzioni al catalogo VCV che contiene le luminosità
bolometriche. Nel caso dello spettro ottenuto con il contributo delle sorgenti nella
Lista 1 non si osserva però una tale risalita; ciò è dovuto al fatto che in quest’ultima
lista le tre sorgenti hanno luminosità pari a circa 1041 erg/s, mentre nella lista ottenuta con le luminosità bolometriche Centaurus A ha L ∼ 1043 erg/s mentre NGC
4945 ha luminosità pari a 2 × 1044 erg/s. Data la potenza maggiore delle sorgenti
vicine in questa lista, è possibile osservare il loro peculiare contributo al flusso a
altissime energie poichè, data la vicinanza, si trovano all’interno della sfera GZK e
il flusso di raggi cosmici da esse provenienti non viene attenuato. Tale contributo
non attenuato dal GZK sarà presente anche nell’esempio fatto con la Lista 1, ma
97
E3 J(E) [eV2 m-2 s-1]
Emax,uni=8x1019 eV Emax,AGN=2x1020 eV
1024
Auger
somma
AGN Lista 1
dist.uniforme
1017
1018
1019
1020
E [eV]
Figura 6.15:
erg/(s
Somma dello spettro da distribuzione uniforme (γ = 2.5, L0 = 1.06 × 1042
e dello spettro delle sorgenti della Lista 1 (γ = 2.1, η = 1.62).
Mpc3 ))
date le luminosità più basse conterà meno nel flusso e non sarà quindi visibile in
corrispondenza dei valori di E 3 J(E) che ci interessano.
Discutiamo ora le scelte effettuate per il parametro Emax ; la scelta iniziale di
un unico valore (2 × 1020 eV) per l’energia massima a cui possono essere accelerati
raggi cosmici da sorgenti della distribuzione uniforme e della distribuzione discreta
è dettata dal fatto che stiamo considerando un’unica classe di candidati a sorgenti
di raggi cosmici.
Come si può vedere nelle figure 6.15, 6.16 e 6.17, nel caso in cui le sorgenti della
distribuzione uniforme accelerassero particelle fino ad una energia massima minore
di quella delle sorgenti discrete, il contributo al flusso totale sarebbe minore e la
struttura visibile nello spettro di Auger sarebbe riprodotta in maniera migliore.
Questo risultato può essere analogamente ottenuto scegliendo lo stesso valore
per l’energia massima di accelerazione per le distribuzioni e un valore più alto del
redshift minimo per la distribuzione uniforme.
Si può inoltre vedere (figura 6.18) che lo stesso risultato della figura 6.15 si
può ottenere abbassando il valore dell’iniezione γ della distribuzione uniforme e
prendendo un valore dell’evoluzione cosmologica diversa da zero poichè questo fa sı̀
che aumenti il contributo delle sorgenti ad alto redshift.
Da questa discussione segue che i parametri che rientrano nei calcoli si riflettono
nello spettro in energia; i parametri più importanti ai fini del lavoro svolto in questa
Tesi sono l’energia massima e il redshift minimo da cui contribuisce la distribuzione
uniforme di sorgenti, in quanto questi determinano la presenza una struttura ben
definita nello spettro, visibile come una discontinuità, che ci possiamo aspettare di
98
E3 J(E) [eV2 m-2 s-1]
Emax,uni=8x1019 eV, Emax,AGN=2x1020 eV
1024
Auger
somma
AGN Lista 1b
dist. uniforme
1017
1018
1019
1020
E [eV]
Figura 6.16:
erg/(s
Somma dello spettro da distribuzione uniforme (γ = 2.5, L0 = 1.06 × 1042
e dello spettro delle sorgenti della Lista 1b (γ = 2.1, η = 4.07 × 10−2 ).
Mpc3 ))
E3 J(E) [eV2 m-2 s-1]
Emax,uni=8x1019 eV, Emax,AGN=2x1020 eV
1024
Auger
somma
AGN Lista X
dist.uniforme
1017
1018
1019
1020
E [eV]
Somma dello spettro da distribuzione uniforme (γ = 2.5, L0 = 1.06 × 1042
erg/(s Mpc3 )) e dello spettro delle sorgenti della Lista X (γ = 2.1, η = 2.14−1 ).
Figura 6.17:
99
E3 J(E) [eV2 m-2 s-1]
Emax,uni=8x1019 eV Emax,AGN=2x1020 eV
1024
Auger
somma
AGN Lista 1
dist.uniforme
1017
1018
1019
1020
E [eV]
Figura 6.18:
erg/(s
Somma dello spettro da distribuzione uniforme (γ = 2.4, L0 = 9.92 × 1040
m = 2.5) e dello spettro delle sorgenti della Lista 1 (γ = 2.1, η = 1.62).
Mpc3 ),
osservare in futuro nello spettro sperimentale. Questo sarà possibile con l’aumento
della statistica in Auger.
La presenza o meno di tale struttura limiterà quindi lo spazio dei parametri
attualmente a nostra disposizione consentendoci di aumentare le informazioni in
nostro possesso riguardo alle sorgenti di raggi cosmici ultra-energetici.
Nelle conclusioni che seguono si riporta una discussione globale riguardo alle
scelte fatte per i parametri da utilizzare nei calcoli, evidenziando appunto la particolare importanza dell’energia massima e del redshift minimo.
100
Conclusioni e sviluppi futuri
Il presente lavoro di Tesi si basa sulle osservazioni dell’esperimento Auger. In
particolare, abbiamo concentrato la nostra attenzione sulle osservazioni relative al
flusso dei raggi cosmici di altissima energia ed alle direzioni di arrivo di tali particelle. Nel capitolo 5 abbiamo discusso i risultati di Auger relativi alle direzioni di
arrivo degli eventi di più alta energia (E > 3 × 1019 eV). Tale studio ha permesso
un’analisi della correlazione delle direzioni di arrivo degli UHECR con le posizioni
di oggetti astrofisici candidati ad essere sorgenti di raggi cosmici.
Lo spettro in energia mostra una soppressione del flusso a energie di circa 4×1019
eV; questo è in accordo con la previsione di Greisen, Zatsepin e Kuz’min (1966) (detta effetto GZK) secondo i quali se i raggi cosmici di altissima energia sono costituiti
prevalentemente da protoni il flusso mostrerà una soppressione intorno a 5 × 1019 eV
a causa delle perdite di energia subite dai protoni per l’interazione con la radiazione
cosmica di fondo (CMBR).
Dallo studio delle direzioni di arrivo degli UHECR in combinazione con le posizioni di sorgenti astrofisiche, Auger ha determinato una correlazione positiva tra
le direzioni di arrivo dei raggi cosmici con energie maggiori di 6 × 1019 eV ed alcuni
nuclei galattici attivi posti a distanze minori di 75 Mpc. Tale risultato è un’ulteriore
conferma dell’anisotropia nelle direzioni di arrivo dei raggi cosmici ad alte energie
come segue dallo studio della dipendenza dall’energia della correlazione del set di
dati con gli AGN del catalogo VCV. I dati di Auger sono compatibili con una distribuzione di sorgenti che segue quella degli AGN ad alte energie con una transizione
verso una distribuzione isotropa a energie minori di 6 × 1019 .
La soppressione del flusso dovuta all’interazione dei raggi cosmici con la CMBR
e’ attesa per energie superiori all’energia di soglia della reazione di fotoproduzione
di π. Come discusso nel capitolo 3, un protone con energia iniziale di 1022 eV perde
energia a causa dell’interazione con la CMBR arrivando ad energie minori della
soglia per la reazione considerata dopo aver percorso circa 50 ÷ 100 Mpc. Dunque,
la rivelazione di raggi cosmici ad energie superiori a 0 5 × 1019 eV sarebbe indice
della presenza di sorgenti entro le distanze citate. Ci possiamo quindi aspettare
di osservare una transizione nella ditribuzione di sorgenti ad energie dell’ordine di
quella prevista dall’effetto GZK.
Le osservazioni di Auger ci offrono, dunque, due evidenze sperimentali: da una
101
parte lo spettro in energia dei raggi cosmici, dall’altra alcune indicazioni sui possibili
siti di accelerazione di raggi cosmici. Lo scopo di questa Tesi e’ proprio la ricerca
di un punto di collegamento tra i fatti osservativi riportati sopra. Cerchiamo infatti di capire se è possibile individuare nello spettro il segnale della transizione tra
due distinte distribuzioni di sorgenti: una isotropa, che ha rilevanza nello spettro di
bassa energia (E < 2 ÷ 3 × 1019 eV), ed una anisotropa dominante ad alta energia
(E > 2 ÷ 3 × 1019 eV), costituita dagli AGN posti entro 50 ÷ 100 Mpc per i quali si
hanno informazioni da catalogo.
Per calcolare lo spettro teorico ci siamo serviti di alcune assunzioni; innanzi
tutto abbiamo considerato solo protoni ed abbiamo utilizzato l’approssimazione di
perdite continue di energia. Le perdite di energia che subiscono i protoni nella
propagazione dalla sorgente all’osservatore sono dovute all’espansione dell’universo
ed all’interazione con la CMBR, da cui si ha produzione di coppie e± e π, quest’ultima dominante oltre 4 × 1019 eV. L’approssimazione di perdite continue di energia
è giustificata dal fatto che le fluttuazioni nel processo di fotoproduzione di π modificano solo debolmente lo spettro atteso, al livello del %, fino alle energie più elevate
(E > 1021 eV).
Nel calcolo dello spettro degli UHECR occorre introdurre anche alcune ipotesi
sulla distribuzione di sorgenti. La ricerca delle correlazioni eseguita da Auger si basa
su un catalogo di nuclei galattici attivi e quasars che può essere considerato completo solo entro distanze dell’ordine di 100 Mpc (corrispondente a redshift 0.024), per
problemi legati alla compilazione stessa del catalogo. Inotre, le correlazioni trovate
da Auger sono con sorgenti entro 75 Mpc, distanza corrispondente a redshift di circa
0.017.
Queste osservazioni suggeriscono il calcolo del flusso atteso assumendo sorgenti da catalogo entro una distanza (redshift) dell’ordine dei 100 Mpc ed una distribuzione omogenea ed uniforme di sorgenti per distanze superiori. Il redshift
minimo al di sopra del quale si assume una distribuzione omogenea ed uniforme
di sorgenti costituisce dunque un parametro da cui dipenderà il calcolo del flusso
teorico.
Un’altra importante caratteristica delle sorgenti da cui dipende il calcolo del
flusso atteso a Terra è l’iniezione, ovvero il numero di raggi cosmici prodotti dalla sorgente nell’unità di tempo. Come discusso nel capitolo 3 tale quantità ha un
andamento in energia tipo legge a potenza con indice spettrale γ. Se consideriamo
i nuclei galattici attivi come possibili sorgenti di raggi cosmici, possiamo immaginare che l’accelerazione avvenga in onde d’urto che si generano, per esempio, nelle
regioni finali dei getti espulsi dai nuclei delle galassie stesse nel mezzo extragalattico. Lo spettro in energia che ne risulta è una legge a potenza e l’indice previsto e’
γ = 2.0 ÷ 2.2.
Come discusso nel capitolo 6, lo spettro di Auger viene meglio descritto, fin dalle
più basse energie, se si assume uno spettro di protoni con iniezione γ = 2.7. Questa
apparente contraddizione con le previsioni teoriche del modello di Fermi al I ordine
può essere spiegata pensando lo spettro totale della distribuzione uniforme come
102
sovrapposizione di spettri di iniezione γ 2.0 ÷ 2.2 di singole sorgenti poste a diverse
distanze e capaci di accelerare particelle a diversi valori massimi di energia. Tale
sovrapposizione, come dimostrato in [44], produce uno spettro efficace di iniezione
con indice spettrale γ > 2.5.
Questo risultato ha un particolare interesse nel nostro studio poichè ci permette
di distinguere due diversi classi di iniezione: la prima associata alla distribuzione
omogenea ed uniforme di sorgenti, per la quale useremo un indice spettrale γ > 2.5,
e la seconda relativa alle sorgenti vicine (entro 100 Mpc) per le quali useremo le
informazioni da catalogo e che, essendo sparse, mostrano ognuna la propria peculiare iniezione con indice spettrale γ < 2.4, come segue dal meccanismo di Fermi al
secondo ordine.
Un altro importante parametro che fissa lo spettro atteso è la luminosità delle
sorgenti e, per la distribuzione uniforme, la densità delle stesse. La densità delle
sorgenti nella distribuzione uniforme si è assunta pari a n0 = 10−5 Mpc−3 , che corrisponde alla densità di AGN stimata fino ad alto redshift. Fissata la densità, si può
stimare l’emissività L0 = n0 L0 confrontando lo spettro teorico con quello sperimentale, fissando in tal modo la luminosità L0 . Nel caso di una distribuzione uniforme
di sorgenti troviamo questi valori: L0 = 1038 ÷ 1043 erg/(sMpc3 ).
Nel caso delle sorgenti discrete il parametro che entra nella determinazione dello
spettro è la luminosità in raggi cosmici L0 . Nei cataloghi utilizzati si avevano a
disposizione le luminosità in fotoni per fissate bande dello spettro. In questo caso,
dunque, si è assunto la luminosità in protoni UHE proporzionale alla luminosità
osservata in fotoni, determinando il coefficiente di proporzionalità dal confronto con
lo spettro di Auger.
In queto contesto e’ stata fatta un’ulteriore semplificazione assumendo che l’efficienza di conversione della potenza della sorgente in luminosità di raggi cosmici
sia la stessa per ogni sorgente da catalogo. In una situazione più realistica, questa
efficienza sarà diversa da sorgente a sorgente.
Un parametro cruciale legato anch’esso alle caratteristiche dell’acceleratore astrofisico e’ l’energia massima a cui tale oggetto è in grado di accelerare raggi cosmici;
questa dipenderà dalle dimensioni della regione accelerante, dall’intensità del campo magnetico presente e dalle perdite di energia cui è soggetta una particella molto
energetica nel sito di accelerazione, come per esempio l’emissione di sincrotrone o la
perdita di energia per interazioni pγ.
Non esiste al momento una conoscenza approfondita dei nuclei galattici attivi
come siti di accelerazione di raggi cosmici; il valore dell’energia massima rimane
quindi un parametro libero, la cui scelta ha delle conseguenze molto importanti
sulle strutture che si manifestano nello spettro, insieme alla scelta del redshift minimo oltre il quale si considera un universo con distribuzione omogenea ed uniforme
di sorgenti.
Come segue dai risultati del capitolo 6, la scelta di tagliare la distribuzione uniforme ad un certo redshift fa sı̀ che il flusso di questa componente venga soppresso
in modo molto ripido; l’energia a cui corrisponde questo cut-off non è però univoca,
103
una volta scelto zmin . Infatti per diverse scelte dell’energia massima a cui possono
essere accelerati i raggi cosmici nella distribuzione isotropa si avranno diversi valori
dell’energia a cui avviene la soppressione del flusso di questa componente.
La scelta dei due parametri zmin ed Emax relativi alla distribuzione uniforme di
sorgenti fissa la presenza di strutture nello spettro dovute alla transizione tra distribuzione isotropa ed anisotropa; infatti, come abbiamo già fatto notare, mentre
lo spettro delle sorgenti più vicine si estende anche nella parte a basse energie, il
cut-off nello spettro della distribuzione uniforme si manifesterà nello spettro totale
come una discontinuità.
Per ciò che concerne le sorgenti vicine il parametro fondamentale che fissa eventuali strutture nello spettro è l’energia massima di iniezione ed in particolare il
rapporto di questa quantità Emax,AGN con l’energia massima Emax,uni associata
alla distribuzione omogenea ed uniforme di sorgenti. Come discusso nel capitolo
6, nel caso in cui l’energia massima delle due distribuzioni venga presa uguale a
2 × 1020 eV, il contributo della componente uniforme è dominante sulle sorgenti
vicine. Per valori piu’ alti dell’energia massima nelle due distribuzioni (prendendo
ancora Emax,uni = Emax,AGN ) la situazione peggiora ulteriormente. Questo caso sembrerebbe in contraddizione con le correlazioni osservate da Auger. Per evidenziare la
presenza di strutture nello spettro dovute all’effetto delle due distinte popolazioni di
sorgenti occorre assumere Emax,uni < Emax,AGN . Nel caso di Emax,uni = 8 × 1019 eV
e Emax,AGN = 2 × 1020 eV si ha il segnale più forte nello spettro compatibile con le
osservazioni di Auger.
Ricordiamo che in questo lavoro abbiamo trattato la parte dello spettro a energie più alte; il problema principale legato a questa parte di spettro è la scarsa
statistica. Come già discusso nel capitolo relativo agli esperimenti sui raggi cosmici,
l’estensione dell’esperimento Auger consentirebbe la rivelazione di circa 50 eventi
all’anno oltre 1020 eV; l’esistenza del cut-off GZK fa sı̀ che il numero di eventi a
queste energie sia invece molto più basso. L’esperimento Auger ha infatti rivelato
un solo evento a energie oltre 1020 eV.
Possiamo quindi giustificare il fatto che lo spettro osservato non mostri chiare
strutture dovute alla transizione tra distribuzione isotropa e distribuzione anisotropa
di sorgenti come conseguenza della scarsa statistica di cui si dispone alle piu’ alte
energie E > 6 × 1019 eV, dove ci aspetteremmo di vedere tale transizione.
D’altra parte questa transizione, come abbiamo dimostrato in questo lavoro, può
produrre delle strutture nello spettro; con l’aumento della statistica in Auger sarà
possibile avere delle informazioni più precise sullo spettro ad altissime energie. Si
avrà quindi la possibilità di stabilire o meno la presenza di tali strutture limitando
in tal modo lo spazio dei parametri del problema.
Questo avra’ conseguenze molto importanti sulla conoscenza degli oggetti candidati a sorgenti di raggi cosmici in quanto si potranno avere delle indicazioni piu’
precise su quei parametri fondamentali per la determinazione delle strutture nello
spettro, primo tra tutti Emax , ma anche zmin .
104
Abbiamo quindi raggiunto una importante conclusione, ovvero il fatto che dallo
spettro in energia dei raggi cosmici ultra-energetici possiamo avere delle informazioni
sulla distribuzione delle sorgenti e sulle caratteristiche dell’accelerazione. Al momento attuale queste informazioni sono ancora nascoste dal basso numero di eventi ad
altissime energie, ma con l’aumento della statistica sarà possibile trarle dallo spettro.
In questo lavoro abbiamo considerato lo spettro osservato da Auger, confrontandolo con il flusso di raggi cosmici ultra-energetici atteso a Terra; abbiamo inoltre
tenuto conto dei risultati di Auger sulla correlazione degli eventi di UHECR con le
posizioni di alcuni AGN come evidenza di anisotropia nelle direzioni di arrivo.
Nel capitolo 5 abbiamo discusso come l’anisotropia può essere studiata confrontando la misura dell’intensita’ dei raggi cosmici da diverse direzioni nel cielo;
per fare ciò è necessario conoscere l’esposizione del rivelatore, ovvero l’area effettiva integrata sul tempo per la rivelazione del flusso da una qualsiasi direzione nel
cielo (Appendice C). Nota l’esposizione, è possibile fare delle previsioni sul numero di
eventi attesi da una particolare direzione; nel nostro caso, sceglieremo delle direzioni
di arrivo coincidenti, entro un certo angolo, con le posizioni dei nuclei galattici attivi
trovati in correlazione. La stima del tempo necessario per rivelare un certo numero
di eventi da una precisa sorgente rappresenta quindi un possibile sviluppo di questa
Tesi.
105
Appendice A
Coefficiente di diffusione
Descriviamo in questa appendice l’interazione tra i raggi cosmici e le turbolenze
del campo magnetico; esistono diverse situazioni in cui si possono avere fluttuazioni
turbolente del campo magnetico, e possono riguardare diverse scale di distanza.
In generale, se il campo magnetico fosse omogeneo, ogni particella di raggi cosmici si muoverebbe lungo il campo magnetico avvitandosi attrono alla direzione del
campo; poichè le linee del campo sono trascinate dal fluido nel suo moto, la particella verrà anch’essa trascinata con il fluido.
La presenza di campi magnetici disomogenei cambia la situazione in quanto
questo effetto genera una deriva della particella non termica da una linea di campo
magnetico all’altra causando il fenomeno della diffusione.
Questo fenomeno è presente su scala galattica ed è dimostrato dal fatto che i
raggi cosmici di basse energie sembrano risiedere all’interno della galassia per tempi
molto maggiori di quelli caratteristici galattici, che sono paragonabili alle dimensioni
del disco e al tempo necessario per attraversarlo.
La struttura della galassia è composta da un disco di raggio 15 kpc e uno spessore
di 200 ÷ 300 pc in corrispondenza della posizione della Terra, che dista 8.5 kpc dal
centro; esiste inoltre una struttura a densità minore del disco che costituisce l’alone
galattico.
Una stima del tempo di fuoriuscita dalla galassia per una particella relativistica
può essere dato da:
rgal
(A.1)
τgal =
c
dove con rgal si indica il raggio del disco; da questa stima si ottiene un valore di
τgal ≈ 5 × 104 anni.
Questo valore è in contrasto con il tempo di residenza stimato dalle abbondanze dei nuclei leggeri (soprattutto Li, Be, B) nei raggi cosmici, che risulta essere
τres ≈ 3.9 × 106 anni per densità tipiche del disco galattico e τres ≈ 2 × 107 anni per
densità tipiche dell’alone.
Da qui risulta quindi che i raggi cosmici vengono confinati all’interno della galassia; l’esistenza di un campo magnetico galattico permette quindi di pensare che le
particelle cariche vengano intrappolate proprio dall’interazione con tale campo.
106
Per valutare il coefficiente di diffusione galattica si può scrivere:
τres
2
rgal
=
Dgal
(A.2)
dove Dgal è il coefficiente di diffusione galattica; utilizzando τres ≈ 3.9 × 106 anni e
le dimensioni del disco galattico si trova una stima per il coefficiente di diffusione:
Dgal ≈ 3 × 1029 cm2 /s.
Per capire a quale energia massima possano arrivare i raggi cosmici accelerati in
ambiente galattico, confrontiamo il tempo di diffusione, ovvero il tempo necessario
per compiere una ciclo down-up-down:
τd =
r2
u2 τd2
D
=
−→ τd = 2
D
D
u
(A.3)
con il tempo di vita della regione acccelerante (in questo caso consideriamo particelle accelerate in resti di supernovae, quindi τSN R ∼ 103 anni). Nell’espressione
precedente r è la distanza che l’onda d’urto copre in τd e u la velocità dell’onda.
Affinchè si verifichi il meccanismo ciclico si deve avere τd < τSN R (utilizziamo
inoltre un valore della velocità dell’onda d’urto u pari a 103 km/s).
Utilizzando il coefficiente di diffusione galattica troviamo però valori dell’energia
massima pari a circa 1 GeV, in contraddizione con le osservazioni sperimantali che
indicano la presenza di protoni di origine galattica fino a energie di 1015 eV.
La soluzione di questo problema è data dall’utilizzo di un coefficiente di diffusione
minore di quello galattico, che spieghi le turbolenze locali del campo magnetico in
resti di supernovae a scale minori di quelle considerate finora.
Si scrive quindi una forma generale del coefficiente di diffusione in questo modo:
!
"2−α
1
rL (E)
D(E) = lc v
(A.4)
3
lc
dove v è la velocità della particella, rL (E) il suo raggio di Larmor e lc la scala
massima della turbolenza del campo magnetico.
Prendendo α = 1 si ottiene il coefficiente di diffusione alla Bohm:
1
D(E) = rL (E)c,
3
(A.5)
dove la velocità della particella è stata presa uguale a c. Scrivendo il raggio di
Larmor in questo modo: rL = 10−6 EGeV Bµ−1 pc e prendendo lc = 1 pc (quindi una
scala più piccola della turbolenza rispetto a quella considerata finora) la diffusione
alla Bohm si può esprimere cosı̀:
D(E) ≈ 1022 Bµ−1 EGeV cm2 /s.
107
(A.6)
Prendendo invece α = 3/2 e lc = 100 pc si ritrova il caso della diffusione galattica;
questo tipo di diffusione è detto diffusione alla Kraichnan.
Un altro regime di diffusione è la diffusione alla Kolmogorov (α = 5/3, D ∝
E 1/3 ).
108
Appendice B
Coordinate galattiche
Lo studio dell’anisotropia dei raggi cosmici di energie ultra-alte necessita dell’utilizzo di un sistema di coordinate con cui si possano descrivere le posizioni di oggetti
extragalattici; si utilizzano quindi le coordinate galattiche, per la cui definizione è
necessario partire dalla definizione delle coordinate equatoriali equinoziali.
Le coordinate equinoziali hanno come cerchio base l’equatore terrestre e come
polo il Polo Nord celeste; prendono origine dal punto d’Ariete (il punto d’incontro
tra l’eclittica e l’equatore terrestre) e sono orientate in senso diretto (cioè verso est).
La coordinata δ (declinazione) è l’angolo misurato sull’arco meridiano per il polo e
sull’equatore si misura invece l’ascensione retta (in unità di tempo).
Per studiare i corpi al di fuori del sistema solare vengono invece utilizzate le coordinate galattiche; il piano di simmetria utilizzato è quello dell’equatore galattico.
Poichè tale piano non è ben individuato, si procede per convenzione. Si fissano le
coordinate equinoziali del polo galattico: αG = 12h 51m ≡ 192.84, δG = 27.07! .7 ≡
27.13, da cui seguono l’ascensione retta del nodo ascendente dell’equatore galattico
sull’equatore celeste αG = 18h 49m e l’inclinazione i = 62.6. L’origine sul piano equatoriale è fissata in modo che la longitudine galattica del nodo ascendente sia lG = 33,
ciò che fisicamente corrisponde a scegliere la direzione del centro della Galassia. Le
coordinate equatoriali del centro galattico risultano allora αGC 0 17h 45m .6 ≡ 266.41,
δGC 0 −2856! .2 ≡ −28.94. A questo punto si possono definire nel modo usuale la
longitudine l e la latitudine b galattiche.
Il legame tra i due sistemi di coordinate è dato dal sistema di equazioni:

 cos b sin(θGC − l) = cos δ sin(α − αGC )
cos b cos(θGC − l) = cos δG sin δ − sin δG cos δ cos(α − αG )
(B.1)

sin b = sin δG sin δ + cos δG cos δ cos(α − αG )
dove θGC è l’angolo di posizione e vale 123°.
109
Figura B.1:
Rappresentazione schematica della sfera celeste vista in coordinate galattiche.
110
Appendice C
Esposizione
Per un osservatorio di raggi cosmici, l’esposizione è una funzione delle coordinate celesti. Misurata in unità di km2 ·anno, dà l’area effettiva integrata sul tempo
per la rivelazione del flusso da una qualsiasi posizione nel cielo. Più spesso si usa
l’esposizione relativa ω, ovvero una funzione adimensionale data dal valore dell’esposizione in un punto divisa per l’esposizione totale nel cielo.
Si può quindi calcolare l’esposizione per un rivelatore che opera in modo continuo; in questo caso, la funzione di esposizione sarà costante nell’ascensione retta.
Supponiamo che il rivelatore si trovi alla latitudine terrestre a0 e che sia completamente efficiente per particelle che arrivano con angoli θ rispetto allo zenith minori
del valore massimo θm ; l’esposizione sarà quindi funzione della sola declinazione δ:
ω(δ) = ω0 (cos(a0 ) cos(δ) sin(αm ) + αm sin(a0 ) sin(δ)),
(C.1)
dove αm è data da:
e:

se ξ(δ) > 1
 0
π
se ξ(δ) < −1
αm =

arccos(ξ(δ)) altrimenti
ξ(δ) =
cos(θm ) − sin(a0 ) sin(δ)
;
cos(a0 ) cos(δ)
ω0 è una costante di normalizzazione ricavabile dalla condizione:
) δmax
ω(δ)dδ = 1
δmin
δmin = l − θmax
δmax = l + θmax
111
(C.2)
(C.3)
(C.4)
Appendice D
Magnitudine e Luminosità
D.1
Luminosità assoluta
La magnitudine apparente è definita in questo modo (formula di Pogson):
m = −2.5 log10 Φ − c
(D.1)
µ = −2.5 log10 I.
(D.5)
dove Φ è il flusso di radiazione di una stella e c è una costante che dipende dalla
scelta dello zero di riferimento.
Da questa definizione si può introdurre il concetto di magnitudine assoluta:
D
M = m − 5 log10
,
(D.2)
10pc
ovvero la magnitudine che avrebbe una stella se posta ad una distanza di 10 pc
dall’osservatore.
La magnitudine assoluta è quindi legata alla luminosità intrinseca della stella
secondo l’equazione:
M" −M
L
= 10 2.5 ;
(D.3)
L%
Per quanto riguarda le galassie, è possibile utilizzare la stessa forma delle equazioni
scritte sopra, tenendo presente che la luminosità viene trovata integrando il profilo
di brillanza.
La brillanza è definita come il flusso per unità di angolo solido:
Φ
(D.4)
I=
∆Ω
e la brillanza per unità di magnitudine:
Se I(r, θ) è la brillanza superficiale nel punto (r, θ), la luminosità totale della galassia
è:
/2π /∞
I(r, θ)rdrdθ
(D.6)
0
0
112
e la magnitudine totale:
m = −2.5 log10 L + c,
(D.7)
stessa forma con cui si definisce la magnitudine di una stella.
A questo punto, è possibile calcolare la luminosità totale della galassia conoscendo la sua magnitudine dalla formula D.3 trovata per le stelle.
Le formula scritte sopra sono relative alla radiazione monocromatica di una certa
lunghezza d’onda, quindi ogni definizione di magnitudine e luminosità si riferisce ad
una particolare banda di osservazione.
La sensibilità del rivelatore è infatti dipendente dalla lunghezza d’onda della radiazione in arrivo; tra i numerosi sistemi fotometrici il più usato è il sistema UBV,
basato su due filtri le cui curve di risposta corrispondono qualitativamente a quella
visuale V, a quella fotografica B (è centrata tra 4000 e 4500 Å) e a quella centrata
nell’ultravioletto vicino U.
D.2
Luminosità bolometrica
La magnitudine bolometrica dà una misura di quanto la stella irraggia su tutto lo
spettro; è quindi possibile porre in relazione la magnitudine assoluta bolometrica con
la luminosità di una stella, definita come potenza elettromagnetica totale irraggiata.
Si prende di solito come campione la luminosità del Sole: L% = 3.8 × 1033 erg/s;
dato che per il Sole Mbol = 4.75 si ha:
Mbol = 4.75 − 2.5 log10
113
L
L%
(D.8)
Bibliografia
[1] T. K. Gaisser, Cosmic Rays and Particle Physics.
Cambridge University Press, 1990.
[2] M. Vietri, Astrofisica delle Alte Energie.
Bollati Boringhieri, 2006.
[3] A. M. Hillas, Can diffusive shock acceleration in supernova remnants account for
high-energy galactic cosmic rays?
J. Phys. G: Nucl. Part. Phys. 31 (2005).
[4] M. S. Longair, High Energy Astrophysics.
Cambridge University Press (2002)
[5] B. Peterson, An introduction to Active galactic Nuclei.
Cambridge University Press (1997)
[6] M. P. Veron-Cetty, P. Veron, A catalogue of quasars and active nuclei: 12th
edition.
Astron. Astrophys. 455 (2006) 773.
[7] R. Antonucci, Unified Models for Active Galactic Nuclei and Quasars.
Annu. Rev. Astron. Astrophys. 1993.31:473-521
[8] G. B. Rybicki, A. P. Lightman, Radiative processes in astrophysics.
John Wiley and Sons, 1979.
[9] P. Bhattacharjiee, G. Sigl, Origin and propagation of extremely high energy cosmic rays.
astro-ph/9811011v2 (1998)
[10] P. L. Biermann, AGN and galactic sites of cosmic ray origin.
astro-ph/9305005v1 (1993)
[11] M. Ostrowski, Acceleration of UHE Cosmic Ray Particles at Relativistic Jets
in Extragalactic Radio Sources.
astro-ph/9803299v1 (1998)
114
[12] F. Casse, A. Marcowith, Astroparticle yeld and transport from extragalactic jet
terminal shocks.
astro-ph/0411395 (2004)
[13] P. L. Biermann, Centaurus A as a source of extragalactic cosmic rays with
arrival energy well beyond the GZK cutoff.
gr-qc/9511031v2 (1996)
[14] M. Lyutikov, R. Ouyed, Inductive acceleration of UHECRs in sheared relativistic jets.
astro-ph/0507620v3 (2007)
[15] D. V. Semikoz, Constraints on top-down models for the origin of UHECR from
the Pierre Auger Observatory data.
astro-ph/0706.2960v1 (2007)
[16] E. W. Kolb, M. S. Turner, The Early Universe.
Westview, 1990.
[17] V. S. Berezinsky, S. I. Grigor’eva A bump in the ultra-high energy cosmic ray
spectrum.
Astron. Astrophys. 199 (1988) 1-12.
[18] V. S. Berezinsky, A. Z. Gazizov, S. I. Grigor’eva On astrophysical solution to
ultra high energy cosmic rays.
Phys. Rev. D74:043005 (2006)
[19] R. Aloisio, V. S. Berezinsky et al. A dip in the UHECR spectrum and the
transition from galactic to extragalactic cosmic rays.
astro-ph/0608219v2 (2006).
[20] A. A. Watson, Extensive Air Showers and Ultra High Energy Cosmic Rays.
2002.
[21] S. Yoshida, H. Dai, The Extremely High Energy Cosmic Rays.
astro-ph/9802294v1 (1998).
[22] http://www-akeno.icrr.u-tokio.ac.jp/AGASA
[23] J. N. Matthews, Description of High-Resolution Fly’s Eye Detector.
Proc. International Cosmic Ray Conference (2001).
[24] K. Kampert, The Pierre Auger Observatory - Status and Prospects.
astro-ph/0501074v1 (2005).
[25] The Pierre Auger Collaboration, Performance of the Fluorescence Detectors of
the Pierre Auger Observatory.
astro-ph/0508389v1 (2005).
115
[26] The Pierre Auger Collaboration, Performance of the Pierre Auger Observatory
Surface Array.
astro-ph/0508466v1 (2005).
[27] P. Sommers, Cosmic Ray Anisotropy Analysis with a Full-Sky Observatory.
astro-ph/0004016v1 (2000).
[28] S. Benzvi, S. Westerhoff, Search for point sources in Auger SD data using a
maximum likelihood method.
Auger GAP Note 2005-058.
[29] S. Mollerach, Studies of clustering in the arrival directions of cosmic rays detected at the Pierre Auger Observatory above 10 EeV.
Proc. International Cosmic Ray Conference (2007).
[30] The Pierre Auger Collaboration, Discriminating among different scenarios for
the correlation of the highest energy Auger events with nearby sources.
(2007, in preparation).
[31] A. Cuoco et al, The footprint of large scale cosmic structure on the ultra-high
energy cosmic ray distribution.
astro-ph/0510765 (2005).
[32] The Pierre Auger Collaboration, Correlation of the highest-energy cosmic rays
with the position of nearby active galactic nuclei.
astro-ph/0712.2843v1 (2007).
[33] The Pierre Auger Collaboration, A prescription for a search for correlation between AGN and Ultra-High Energy Cosmic Rays with the Pierre Auger
Observatory.
[34] M. R. George et al, On Active Galactic Nuclei as Sources of Ultra-High Energy
Cosmic Rays.
astro-ph/0805.2053v1 (2008).
[35] J. Tueller et al, Swift BAT survey of AGN.
astro-ph/0711.4130v2 (2008).
[36] I. Zaw et al., Galaxies correlating with ultra-high energy cosmic rays.
(2008).
[37] G. R. Farrar, A Gruzinov, Giant AGN flares and cosmic ray bursts.
astro-ph/0802.1074v2 (2008).
[38] G. Ghisellini et al, Ultra-High Energy Cosmic Rays, Spiral Galaxies and Magnetars.
astro-ph/0806.2393v1 (2008).
116
[39] The High resolution Fly’s Eye Collaboration, Search for correlation between
HiRes stereo events and active galactic nuclei.
astro-ph/0804.0382v1 (2008).
[40] T. Yamamoto, The UHECR spectrum measured at the Pierre Auger Observatory and its astrophysical implications.
Proc. International Cosmic Ray Conference (2007).
[41] M. Roth, Measurement of the UHECR energy spectrum using data from Surface
Detector of the Pierre Auger Observatory.
Proc. International Cosmic Ray Conference (2007).
[42] The Pierre Auger collaboration, Observation of the suppression of the flux of
cosmic rays above 4 × 1019 eV.
astro-ph/08064302v1 (2008)
[43] M. Kachelriess, D.V. Semikoz, Ultra-high energy cosmic rays from a finite number of point sources.
Astropart.Phys. 23:486-492 (2005).
[44] M. Kachelriess, D.V. Semikoz, Reconciling the ultra-high energy cosmic ray
spectrum with Fermi shock acceleration.
astro-ph/0510188v2 (2005).
117