Sovrapposizione di onde sinusoidali
Consideriamo due onde sinusoidali che si propagano verso destra con stessa f, λ e ampiezza ma
con differenza di fase φ:
y1 = Asen(kx − ωt)
y 2 = Asen(kx − ωt + φ )
La funzione d’onda risultante sarà:
y = y1 + y 2 = A[sen(kx − ωt) + sen(kx − ωt + φ )
a −b
a+b
)sen(
)
Dall’identità: sena + senb = 2cos(
2
2
φ
φ
y = 2Acos( )sen(kx − ωt + )
2
2
€
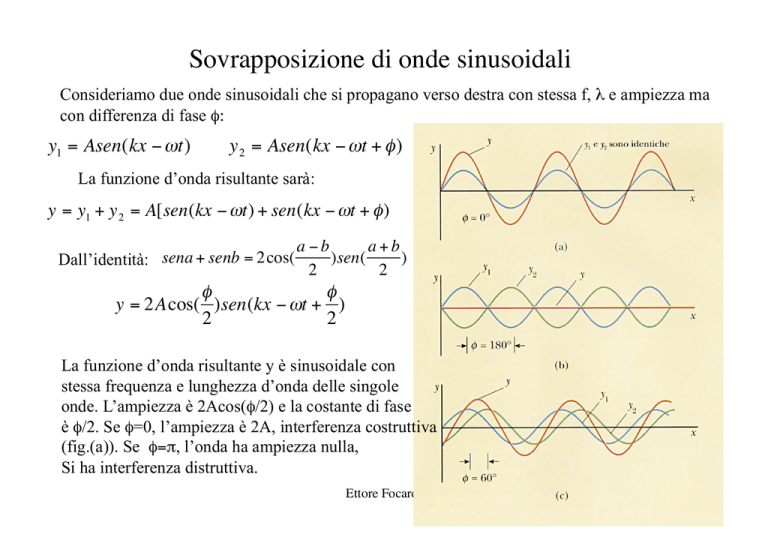
La funzione d’onda risultante y è sinusoidale con
stessa frequenza e lunghezza d’onda delle singole
€ onde. L’ampiezza è 2Acos(φ/2) e la costante di fase
è φ/2. Se φ=0, l’ampiezza è 2A, interferenza costruttiva
(fig.(a)). Se φ=π, l’onda ha ampiezza nulla,
Si ha interferenza distruttiva.
Ettore Focardi
1
Onde stazionarie
Supponiamo di avere due onde identiche che si propagano nel mezzo in direzioni
opposte.
y1 = Asen(kx − ωt)
y 2 = Asen(kx + ωt)
y = y1 + y 2 = Asen(kx − ωt) + Asen(kx + ωt)
y = (2Asenkx)cosωt
Ricordando sen (a±b)= sena cosb ± cosa senb si ha:
€
€
Onda stazionaria
€
non rappresenta un’onda che
si propaga. Particolare tipo
di moto armonico. Particella
mezzo oscilla con stessa ω.
L’ampiezza del moto
armonico della particella
dipende dalla posizione x
della stessa. L’oscillazione
avviene all’interno della
funzione inviluppo 2Asenkx
Minimo spostamento per kx= π, 2π,etc. x=λ/2, λ,..=nλ/2 n=0,1,2…. Nodi
Massimo spostamento per kx=π/2,3π/2,.. x=λ/4,3 λ/4,..=nλ/4 n=1,3,5… antinodi (ventri)
Ettore Focardi
2
Soluzione: onda elettromagnetica piana
La soluzione più semplice delle due equazioni per E e B è un’onda piana sinusoidale in cui
le ampiezze dei campi E e B variano con x e t secondo le espressioni:
E = E max cos(kx − ωt)
B = Bmax cos(kx − ωt)
k=2π/λ è il numero d’onda e
ω=2πf è la pulsazione, con f frequenza dell’onda.
ω 2πf
=
= λf = c
k 2π / λ
valida per ogni onda
In figura è€rappresentata schematicamente un’onda elettromagnetica piana in un certo istante,
polarizzata linearmente, che si propaga con velocità
c nel verso positivo dell’asse x.
€
y
Eseguendo le derivate parziali rispetto a x e t si ha:
z
x
€
∂E
∂B
= −kE max sen(kx − ωt)
= ωBmax sen(kx − ωt)
∂x
∂t
∂E
∂B
=−
che€ sostituite in
danno in ogni istante:
∂x
∂t
E
ω
kE max = ωBmax → max = = c
Bmax
€
e quindi
€
E max E
= =c
Bmax B
k
in ogni istante in un’onda
e.m.il rapporto E/B=c. Le onde e.m. obbediscono
al€principio di sovrapposizione.
Ettore Focardi
3
esempio
Un’onda e.m. piana sinusoidale di frequenza f=40 MHz si propaga nel vuoto in direzione x.
Trovare lunghezza d’onda e periodo. In un certo punto ed istante il campo E raggiunge il
massimo Emax=750 N/C con verso y positivo. Trovare valore e verso di B in quella posizione ed
istante.
da c=λf si ha:
c 3⋅ 10 8 m /s
λ= =
= 7.5m
f
4⋅ 10 7 s−1
Il periodo dell’onda è l’inverso della frequenza:
€
1
1
−8
T= =
7 −1 = 2.5⋅ 10 s = 25 ns
f 4⋅ 10 s
Dalla relazione tra E e B si ha: Bmax =
E max
750N /C
=
= 2.5⋅ 10 −6 T
8
c
3⋅ 10 m /s
€
Le espressioni analitiche di B ed E sono allora:
E = E max €
cos(kx − ωt) = (750N /C)cos(kx − ωt)
ω = 2πf = 2π (4⋅ 10 7 s−1 ) = 2.51⋅ 10 8 rad /s
2π
2π
k=
=
= 0.838rad /m
λ 7.5m
€
€
B = Bmax cos(kx − ωt) = (2.5⋅ 10 −6 T)cos(kx − ωt)
Ettore Focardi
4
Vettore di Poynting
Le onde e.m. trasportano energia per cui, propagandosi nello spazio, possono trasferire energia
agli oggetti che incontrano nel loro cammino. Il flusso di energia per unità di tempo di un’onda
e.m. è descritto dal vettore S, vettore di Poynting, definito come:
1
S≡
E∧B
µ0
Il modulo del vettore di Poynting è uguale al flusso di energia che passa nell’unità di tempo
attraverso l’unità di area di una superficie ⊥ alla direzione di propagazione dell’onda,
€ per unità di area.
Rappresenta quindi la potenza
Verso e direzione del vettore coincidono con il verso e direzione di propagazione dell’onda.
[S]= J/(s m2)= W/m2
€
E ∧ B = EB
Calcoliamo |S| per un’onda e.m. piana per cui
EB
In questo caso è:
ma dato che B/E=c è:
S =
µ0
E2
c
S=
= B2
€
µ0c µ0
valore di S in ogni istante
€
Ettore Focardi
€
5
€
Energia trasportata dalle onde elettromagnetiche
Per un’onda e.m. piana sinusoidale la quantità più interessante è il <S> nel tempo, calcolato
su uno o più cicli, chiamato l’intensità I dell’onda:
1 t +T EB
E B
I =< S >= ∫
dt = max max
T t µ0
Tµ 0
∫
t +T
t
E max Bmax T E max Bmax E 2 max
c 2
cos (kx − ωt)dt =
=
=
=
B max
Tµ 0 2
2 µ0
2 µ0c 2 µ0
2
Ricordiamo che la densità di energia uE=1/2ε0E2 e che uB=1/(2µ0)B2.
Per un’onda e.m. piana dalle relazioni B=E/c e c=1/√(µ0ε0) si ha:
uB =
( E c )2
2 µ0
=
µ0ε 0 2 1
E = ε 0 E 2 = uE
2 µ0
2
In un’onda e.m. piana, la densità di energia associata al campo magnetico è uguale, istante per
istante, alla densità di energia associata al campo elettrico.
La densità istantanea
u=uE+uB=ε0E2=B2/µ0
€ totale di energia u=uE+uB:
Se facciamo la media di questa quantità si ottiene sempre il fattore ½, quindi l’energia totale media
per unità di volume è: umed=ε0(E2)med=1/2ε0Ε2max=B2max/2µ0 da cui si ha:
I = Smed=c umed
L’intensità di un’onda e.m.è uguale al prodotto della densità di energia media per la velocità della
Ettore Focardi
6
luce.
Quantità di moto e pressione di radiazione
Le onde e.m. trasportano anche quantità di moto. Se un’onda incide su una superficie esercita
una pressione.
Supponiamo che l’onda colpisca la superficie perpendicolarmente e che essa assorba tutta la
energia incidente U in un certo tempo t.
Maxwell dimostrò che la quantità di moto totale p trasportata su questa superficie ha modulo
p = U/c
La pressione sulla superficie è definita come P=F/A= (1/A)dp/dt=(1/A)(d/dt)(U/c)=(dU/dt)/cA,
Ma (dU/dt)/A è energia per s per unita’ di area, cioè il modulo del vettore di Poynting è:
P=S/c
Se la superficie è perfettamente riflettente(specchio) e l’incidenza è normale, la p trasferita in t
è doppia (p luce incidente + p luce riflessa) p=2U/c.
La quantità di moto trasferita ad una superficie arbitraria varia tra U/c e 2U/c a seconda del
potere riflettente della superficie. La pressione di radiazione
su superficie perfettamente riflettente e ⊥ è:
P=2S/c
Nasa ha usato p trasferita da Sole
ai pannelli solari
€ di Mariner 10
per piccole correzioni di rotta
pannelli solari Mariner 10
vicino Mercurio.
Apparecchio per la misura della
pressione di radiazione
Ettore Focardi
7
esempio
Pressione prodotta da un puntatore laser.
Se un puntatore laser di potenza P=3 mW produce un punto luminoso di 2 mm di diametro,
trovare la pressione di radiazione nel caso in cui lo schermo riflette il 70% della luce incidente.
Occorre trovare il vettore di Poynting del fascio dividendo la potenza media emessa dalle onde
e.m. per l’area della sezione trasversa:
P
P
3⋅ 10 −3 W
S= = 2 =
= 955W /m 2
1
A πr
π ( 2⋅ 10 −3 m)
2
Questa è circa l’intensità della luce del Sole sulla superficie terrestre. Per questo è pericoloso
puntare il fascio laser verso gli occhi dei presenti; potrebbe essere più dannoso che guardare
€
direttamente il sole. Calcoliamo
ora la pressione.
Supponiamo che la superficie assorba il fascio e quindi P=S/c. Se essa riflette solo una
frazione f, la pressione dovuta al fascio riflesso è P=fS/c. Da qui la pressione totale:
S
S
S
955W /m 2
P = + f = (1+ f ) = (1+ 0.7)
= 5.4⋅ 10 −6 N /m 2
8
c
c
c
3⋅ 10 m /s
(valore piccolo, confronto con pressione atmosferica 105 N/m2).
€
Ettore Focardi
8
Onde elettromagnetiche da un’antenna
Ogni volta che la corrente che attraversa un filo conduttore, varia nel tempo, il filo emette una
radiazione elettromagnetica. Il meccanismo di produzione di tale radiazione è l’accelerazione di
una particella carica. Una tensione alternata applicata ai fili di un’antenna mette in oscillazione
le cariche elettriche nell’antenna. Questa è la tecnica usata per accelerare cariche ed è la
sorgente delle onde radio emesse dall’antenna di trasmissione di una stazione radio.
Campo elettrico prodotto da cariche che oscillano sull’antenna. Il campo si allontana
dall’antenna alla velocità della luce. Un campo magnetico oscillante ⊥ al piano accompagna
il campo elettrico oscillante.
Ettore Focardi
9
Spettro onde elettromagnetiche
I vari tipi di onde dello spettro elettromagnetico
sono classificati in figura.
La radiazione è prodotta da cariche accelerate.
onde radio: 0.1-104 m comunicazione radio-TV
Microonde: 0.3-10-4m sistemi radar, cucina
Infrarosse: 10-3-7 10-7 m onde prodotte dai corpi a
T ambiente e facilmente assorbite dai
materiali riscaldamento. Terapia fisica.
Visibile: 7 10-7 (rosso)- 4 10-7 (violetto) m
sensibilità massima occhio ~5.5 10-7 m
palle da tennis di colore giallo-verde, perchè?
Ultravioletto: 4 10-7- 6 10-10 m . Sole sorgente UV
scottatura pelle. Parte delle radiazione da Sole
è assorbita nella stratosfera dall’ozono (O3).
Tale schermo converte radiazione UV (pericolosa)
in calore. Buco dell’Ozono meno protezione
Raggi X: 10-8-10-12 m prodotti da accelerazione di efrenati in lastra metallica. Diagnosi e terapia medica
Raggi γ : 10-10-10-14 m. Onde prodotte da nuclei
radioattivi.
Ettore Focardi
10












