Soluzione e commenti al fac

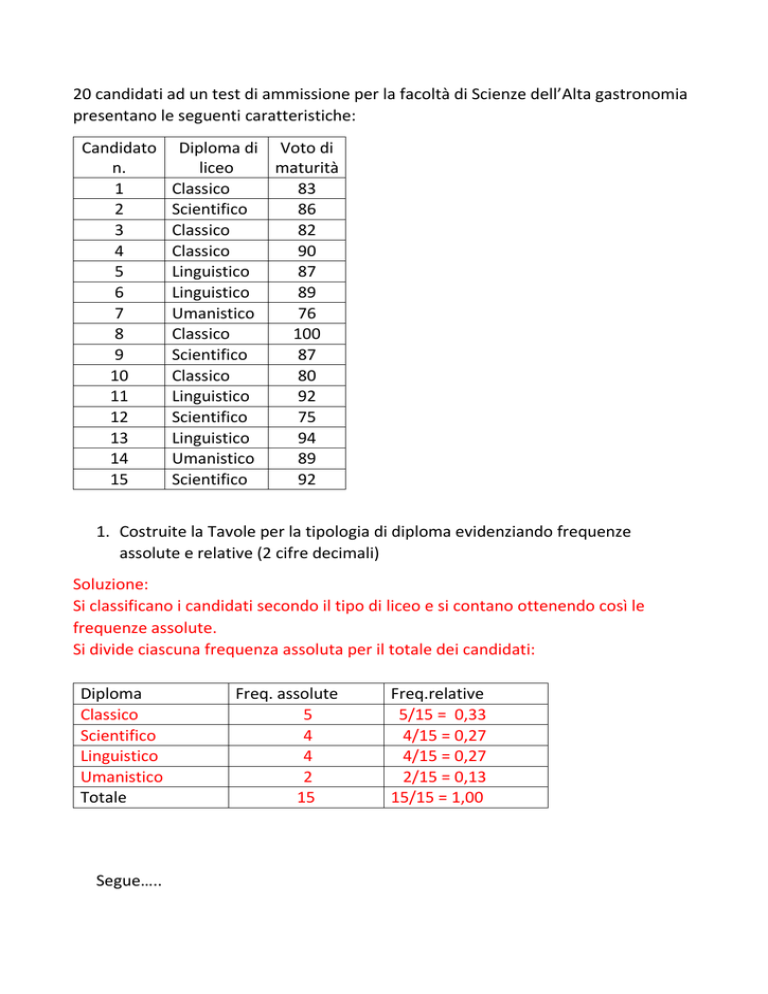
20 candidati ad un test di ammissione per la facoltà di Scienze dell’Alta gastronomia
presentano le seguenti caratteristiche:
Candidato
n.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Diploma di Voto di
liceo
maturità
Classico
83
Scientifico
86
Classico
82
Classico
90
Linguistico
87
Linguistico
89
Umanistico
76
Classico
100
Scientifico
87
Classico
80
Linguistico
92
Scientifico
75
Linguistico
94
Umanistico
89
Scientifico
92
1. Costruite la Tavole per la tipologia di diploma evidenziando frequenze
assolute e relative (2 cifre decimali)
Soluzione:
Si classificano i candidati secondo il tipo di liceo e si contano ottenendo così le
frequenze assolute.
Si divide ciascuna frequenza assoluta per il totale dei candidati:
Diploma
Classico
Scientifico
Linguistico
Umanistico
Totale
Segue…..
Freq. assolute
5
4
4
2
15
Freq.relative
5/15 = 0,33
4/15 = 0,27
4/15 = 0,27
2/15 = 0,13
15/15 = 1,00
2. Calcolate Media Mediana e Varianza per il diploma di liceo Classico
Media
Mediana
Varianza
87
83
53,6
I dati da considerare sono quelli relativi ai soli candidati provenienti dal liceo
classico: (conviene ordinarli secondo il voto per il calcolo della MEDIANA)
Candidato Diploma di Voto di
n.
liceo
maturità
10
Classico
80
3
Classico
82
1
Classico
83
4
Classico
90
8
Classico
100
5
1. Calcolo della MEDIA:
M 
x
i 1
i
5
80  82  83  90  100 435


 87
5
5
2. Calcolo Mediana : il voto che “divide in due” la distribuzione è quello centrale
nella sequenza ORDINATA cioè 83
3. Calcolo della Varianza (V)
Media dei quadrati degli scarti da M:
5
 (x
 M )2
(80  87) 2  (82  87) 2  (83  87) 2  (90  87) 2  (100  87) 2
V


5
5
(7) 2  (5) 2  (4) 2  (3) 2  (13) 2  49  25  16  9  169 268



 53,6
5
5
5
i 1
i