Esercizi su statica e moto di cariche in campi elettrici
[1] Una sferetta di massa 5 g, carica negativa 1 µC, è sospesa per mezzo di un filo di lunghezza 1 m in un campo
elettrico uniforme come nella figura seguente. L’angolo che il filo forma con la verticale misura 30◦ .
• Rappresenta tutte le forze che agiscono sulla sferetta.
• Calcola l’intensità del campo elettrico.
[2] Un protone è immerso in un campo elettrico uniforme ed è in equilibrio con il suo peso. Determina intensità,
direzione e verso del campo elettrico.
[1,03 · 10−7 N/C, verticale verso l’alto]
[3] Un protone, inizialmente fermo, viene accelerato da un campo elettrico di intensità 500 N/C per un tratto di 20
cm. Calcola:
• l’accelerazione del protone;
• la velocità e l’energia cinetica finale del protone.
[4,8 · 1010 m/s2 ; 1,4 · 105 m/s; 1,6 · 10−17 J]
[4] Un dipolo elettrico è formato da due cariche opposte di modulo 2 · 10−6 C fissate a 4 cm di distanza. Esso si
trova in un campo elettrico uniforme di intensità 3 · 104 N/C ed è orientato perpendicolarmente alle linee del
campo.
• Che cosa succede al dipolo?
• Qual è il massimo valore del momento che il campo esercita sul dipolo? (ricorda che il momento è il prodotto
di forza e braccio...)
[2,4 · 10−3 N·m]
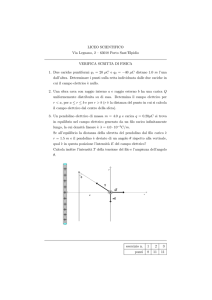
[5] Ioni positivi di carica q e massa m attraversano un piccolo foro, A, con velocità iniziale v0 . Entrano in una zona
in cui è presente un campo elettrico uniforme di intensità E .
In funzione dei parametri assegnati (m, q, E , d), calcola:
• l’accelerazione degli ioni;
• la legge oraria con cui si muove uno ione;
• l’energia cinetica di uno ione e la sua velocità nel punto B.
[qE /m; v0 t + 12 at 2 ; Ec = 12 mv02 + qEd]
[6] Una goccia d’olio di densità d = 8 · 102 kg/m3 ha forma sferica e raggio r = 1 µm ed è dotata di una carica
elettrica q. Introdotta in una regione di spazio in cui è presente un campo elettrico E = 2,05 · 104 N/C uniforme,
verticale e diretto verso l’alto, resta ferma in equilibrio.
Calcola il valore di q. [è una situazione analoga a quella dell’esperimento di Millikan...]
[7] Un protone, inizialmente fermo in un campo elettrico uniforme di intensità 25 N/C, viene lasciato libero e
accelerato dalla forza del campo. Con quale velocità si muove dopo un millesimo di secondo?
[2,4 · 106 m/s]
[8] Una carica di 10−8 C possiede un’energia cinetica di 2 · 10−5 J. Entra in un campo elettrico uniforme lungo una
linea di forza, ma in verso opposto al campo. L’intensità del campo è 5000 N/C.
Calcola lo spazio che percorre prima di fermarsi. [applica la conservazione dell’energia...]
[9] Un protone arriva nel punto A con velocità v0 formante un angolo α con la direzione orizzontale. Viene deflesso
da un campo elettrico uniforme e arriva nel punto B.
In funzione dei parametri assegnati (α, E , `), calcola:
• l’accelerazione degli ioni;
• la legge oraria con cui si muove uno ione;
• l’energia cinetica di uno ione e la sua velocità nel punto B.
[le equazioni del moto sono x = v0 cos αt, y = − 12 at 2 + v0 sin αt... il punto di
massima altezza si ha per x = `/2...]
[10] Fra le due piastre della figura è presente un campo elettrico uniforme di intensità 30000 N/C. Un elettrone arriva
nel punto M con una velocità di 1,2 · 106 m/s. Viene deviato dalla forza elettrica ed esce dal campo nel punto
N, che si trova 4 cm più in basso del punto M.
Calcola la velocità dell’elettrone nel punto N, trascurando la forza peso. [applica la
conservazione dell’energia, scegliendo opportunamente lo 0 dell’energia potenziale
elettrica...]
[11] Una carica di −2 µC si trova a 20 cm da una carica fissa di +10 µC. La prima varica viene spostata in un punto
che dista 70 cm dalla carica fissa.
• Perché per compiere questa trasformazione è stato necessario compiere lavoro sul sistema dall’esterno?
• L’energia potenziale del sistema è aumentata o diminuita? Perché?
• Di quanto è variata l’energia potenziale del sistema?
• Quale lavoro è stato fatto sulla carica libera?
[0,64 J; 0,64 J]
[12] Una particella di massa m e carica q, inizialmente a riposo, è libera di muoversi in un campo elettrico di intensità
E . Dopo un tempo t, qual è l’energia cinetica della particella?
Eq 2 m
2t 2
E 2q2t 2
2m
2E 2 t 2
mq
Eqm
2t