Velocità

La Forza
Richiami di Fisica Generale – Cinematica e Dinamica - 1
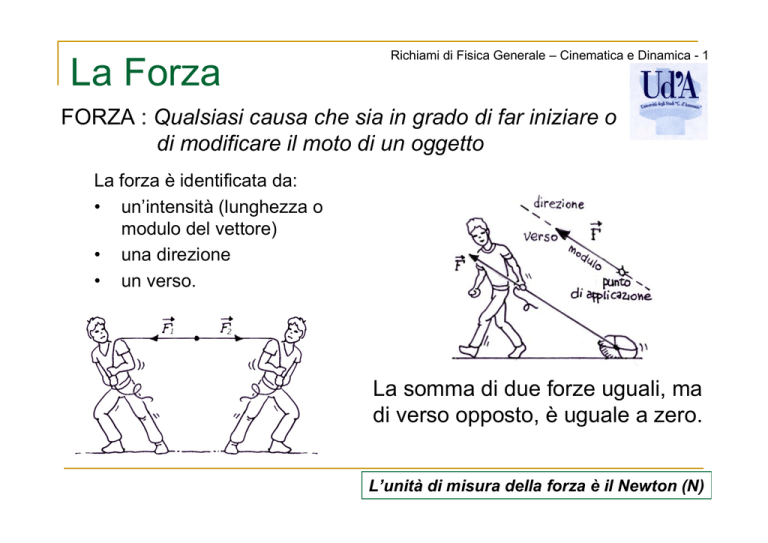
FORZA : Qualsiasi causa che sia in grado di far iniziare o
di modificare il moto di un oggetto
La forza è identificata da:
• un’intensità (lunghezza o
modulo del vettore)
• una direzione
• un verso.
La somma di due forze uguali, ma
di verso opposto, è uguale a zero.
L’unità di misura della forza è il Newton (N)
La Forza Peso
Richiami di Fisica Generale – Cinematica e Dinamica - 2
E’ la forza che si esercita in un campo gravitazionale a causa
dell’attrazione reciproca delle masse. Sulla Terra è quella che
comunemente viene detta “Forza Peso”, e corrisponde alla forza di
attrazione che la massa terrestre esercita su ogni corpo posto nelle sue
vicinanze.
La sua intensità è proporzionale al prodotto
della massa, proprietà del corpo, per
l’accelerazione gravitazionale, dipendente
dalla massa della Terra e dalla distanza fra
il centro di quest’ultima e la massa
dell’oggetto.
Accelerazione gravitazionale
[
g = 9,81 m / s 2
]
G
G
P = mg
Analisi Dimensionale
m
[N ] = [kg ]  2 
s 
La Forza Elastica
Richiami di Fisica Generale – Cinematica e Dinamica - 3
La forza elastica è la forza di reazione che una molla esercita
quando proviamo ad allungarla.
La sua intensità è proporzionale al prodotto della
costante elastica della molla per l’allungamento
della stessa (Legge di Hooke).
Fe = k ∆l
La legge di Hooke vale fino a che l’allungamento della
molla non sia tale da provocare una deformazione
permanente della stessa (deformazione plastica)
Analisi Dimensionale
N 
[k ] =  
m
Richiami di Fisica Generale – Cinematica e Dinamica - 4
La Forza di Attrito Radente
Quando proviamo a far strisciare un
corpo su di una superficie siamo costretti
ad applicare una forza. Ciò è dovuto al
fatto che sulle superfici di contatto dei
due materiali si sono creati dei
microlegami che impediscono lo
strisciamento del corpo.
E’ proprio la rottura dei microlegami l’origine della forza di Attrito; che
nel caso descritto viene chiamato Attrito Radente.
Dove Fv è la forza verticale agente sul corpo che
striscia, in direzione ortogonale al piano di
strisciamento, e µs è il coefficiente di attrito statico
R
s v radente. Nell’esempio riportato in figura la forza
verticale coincide con la forza peso esercitata dal
corpo sulla superficie di scorrimento.
F =µ F
Richiami di Fisica Generale – Cinematica e Dinamica - 5
La Forza di Attrito Volvente
L’attrito radente non è l’unico tipo di forza di attrito, l’attrito volvente
ad esempio è parimenti importante. Esso si verifica quando un corpo
viene fatto rotolare su di una superficie.
FV =
µV
r
Fv
Dove Fv è la forza verticale agente sul corpo che
striscia, µV è il coefficiente di attrito volvente ed r
è il raggio dell’oggetto che rotola.
Anche i fluidi esercitano
una forza di attrito sui corpi
a causa della propria
viscosità
Esempio
Richiami di Fisica Generale – Cinematica e Dinamica - 6
Coefficienti di Attrito
Un’autovettura di peso
P è dotata di ruote di 0,3
metri di raggio.
Calcolare il rapporto fra
l’attrito radente e quello
volvente (µV =0,01 m).
0,4
FR µ d P
=
=
= 12
FV µ V P 0,01
0,3
r
Materiali
µs
µd
Acciaio su ghiaccio
0,1
0,05
Acciaio su acciaio
0,6
0,4
Acciaio su acciaio lubrificato
0,1
0,05
Pneumatici su asfalto
0,6
0,4
Il coefficiente di attrito
radente assume due valori
a seconda che il solido sia
fermo (µs – attrito statico),
o in movimento (µd – attrito
dinamico)
Richiami di Fisica Generale – Cinematica e Dinamica - 7
Forza di attrito in un Fluido
La viscosità è l’origine dei fenomeni di separazione dello strato limite che si viene a
formare nella zona di contatto fra il solido ed il fluido stesso.
In special modo nei corpi tozzi, la separazione da origine ad una scia in cui sono
presenti due vortici temporalmente sfalsati, a tale scia si da il nome di Scia di Von
Karman.
Il fenomeno induce fenomeni oscillatori nel sistema e produce valori elevati della
resistenza aerodinamica.
Richiami di Fisica Generale – Cinematica e Dinamica - 8
Tacoma Narrows Bridge (1940)
Il crollo del ponte sospeso Tacoma Narrows
La mattina del 7 novembre 1940, dopo soli 4 mesi dalla sua inaugurazione, il Tacoma Narrows
Bridge crollò"abbattuto" da un vento che soffiava ad una velocità di soli 50-60 km/h.
Le ragioni del crollo sono da ricercare nell’instabilità aeroelastica della struttura che, soggetta ad
oscillazioni torsionali amplificate, ha portato alla rottura dei cavi di sostegno e quindi al collasso
strutturale.
Le oscillazioni aeroelastiche furono indotte dalla presenza di un Flutter associato anche allo
sviluppo di vortici di Von Karman che amplificarono le oscillazioni della struttura.
Solo un aumento della rigidezza strutturale, specie a torsione, avrebbe potuto impedire il
drammatico cedimento della struttura.
DATI GENERALI
„Progettista: Dott. Ing. Leon Moisseiff
„Freccia dei cavi portanti: 70 metri
„Materiali: acciaio e calcestruzzo
„Data del completamento: 1940
„Campata centrale: 853 metri
„Data del crollo: 7/11/1940
„Tipologia: ponte sospeso
„Localita': Stati Uniti
La Velocità (1)
Richiami di Fisica Generale – Cinematica e Dinamica - 9
La Velocità rappresenta la distanza percorsa
nell’unità di tempo; essa esprime la Rapidità
con cui un’oggetto si muove. E’ una
grandezza vettoriale
Tempo (min) Posizione (km) Tempo (s)
0
2
0
3
3
180
6
4
360
9
5
540
12
6
720
15
7
900
18
8
1080
21
9
1260
24
10
1440
G ∆ sG
V=
∆t
Posizione (m) Velocità (m/s)
2000
0
3000
5.6
4000
5.6
5000
5.6
6000
5.6
7000
5.6
8000
5.6
9000
5.6
10000
5.6
[m / s ]
La Velocità (2)
Richiami di Fisica Generale – Cinematica e Dinamica - 10
La velocità di un punto può essere interpretata come la
pendenza locale della curva spostamento - tempo.
Pendenza del tratto a velocità costante
∆ s sen(α )
V =
=
= tg (α )
∆t
cos(α )
Velocità istantanea
ds
V =
dt
ds
= Pendenza locale
dt
Richiami di Fisica Generale – Cinematica e Dinamica - 11
Esempio
Distanza (m)
0
5
13
20
26
35
Tempo (s)
0
1
2
4
5
6
6
5
4
Tempo (s)
Un’autovettura è in movimento a
velocità variabile lungo un
rettilineo, se le coordinate spazio
temporali del veicolo sono quelle
riportate nella tabella sottostante,
calcolare la distribuzione di
velocità ed il valore medio della
stessa.
3
2
1
0
0
5
10
15
20
25
30
Posizione (m)
G ds
s fin − sin
V =
= lim
dt ( t fin −tin )→0 t fin − tin
35
Richiami di Fisica Generale – Cinematica e Dinamica - 12
Soluzione
Tempo (s)
0
1
2
4
5
6
Velocità (m/s) Interv. di tempo (s)
5.00
1
8.00
1
3.50
2
6.00
1
9.00
1
10
9
8
Velocità (m/s)
Distanza (m)
0
5
13
20
26
35
7
6
5
4
3
2
1
0
0
1
2
3
Tempo (s)
Vel. Media
5.83
m/s
4
5
6
Accelerazione (1)
Richiami di Fisica Generale – Cinematica e Dinamica - 13
L’Accelerazione rappresenta il rapporto fra la variazione di
velocità e l’intervallo di tempo in cui tale variazione avviene.
G
∆V
a =
∆t
G
m / s 2 
Come per la velocità, l’accelerazione
istantanea rappresenta la pendenza
locale della curva Velocità - tempo
G
dV
m / s 2 
a =
dt
G
Accelerazione (2)
Richiami di Fisica Generale – Cinematica e Dinamica - 14
L’accelerazione locale
è rappresentata dalla
derivata della curva
velocità - tempo.
dV
a=
dt
Quando la pendenza di tale curva è negativa
siamo in presenza di una decelerazione.
Richiami di Fisica Generale – Cinematica e Dinamica - 15
Accelerazione (3)
Una sfera viene lanciata con velocità V0 verso l’alto, calcolare dopo
quanto tempo si fermerà, prima di invertire il moto. Calcolare inoltre
a quale altezza arriverà la sfera.
L’unica accelerazione agente sulla sfera è
quella gravitazionale ed ha verso opposto alla
velocità V0.
y
g
0 −V 0
V −V in
−g = fin
=
t fin − t in t fin − 0
t fin
V0
=
g
t
V0
y − y 0 = y = ∫V dt
t
0
V −V 0 = − ∫ g dt = −g ⋅ (t − t 0 ) = − g ⋅ t
t
0
y = ∫ (V 0 − g ⋅ t ) dt = V 0 ⋅ t − g ⋅
0
t2
2
Accelerazione (4)
Richiami di Fisica Generale – Cinematica e Dinamica - 16
Una sfera viene lanciata, con angolo di inclinazione pari ad α, e velocità
V0, verso l’alto; calcolare l’altezza massima raggiunta ed a che distanza,
lungo l’asse x, dall’origine raggiungerà il terreno.
V x = cos tan te =
x −0 x
= = V 0 cos α
t −0 t
V y = V 0 sen α − g t
g
Vy
V0
V 0 cos α
Se d è la distanza a cui la sfera ritorna al suolo avremo che a metà di
questa distanza la velocità lungo l’asse –y- è uguale a zero; da cui:
t max =
y
t =
x
d /2
V 0 cos α
t max
y max = V 0 sen α ⋅ t max − g ⋅
t max 2
= 0 = V 0 sen α − g t max = V 0 sen α − g
α
d =
x
2V 0 2 sen α cos α
g
2
d /2
V 0 cos α
Una volta calcolato d è possibile
determinare il valore di tmax e,
quindi, di y max.
Richiami di Fisica Generale – Cinematica e Dinamica - 17
La Forza d’Inerzia (1)
In un campo Inerziale un corpo è fermo o si muove di moto
rettilineo uniforme fino a che su di esso non agisca una forza che
lo faccia cambiare di stato. Qualora agisca una forza su un corpo
di massa “m” esso riceverà un’accelerazione “a” tale che:
G
G
F =ma
in questo caso si
parla di Forza di
Inerzia.
Per dimostrare la veridicità della
formula sopra riportata proviamo a
prendere un disco forato sopra il quale
è fissato un contenitore sferico pieno
di anidride carbonica allo stato
solido.Quest’ultima andando in
sublimazione genera un getto di gas
che mantiene in sospensione il disco.
Richiami di Fisica Generale – Cinematica e Dinamica - 18
La Forza d’Inerzia (2)
Il getto di gas annulla la forza risultante
verticale, rendendo così trascurabile
qualunque forza di attrito.
A questo punto leghiamo con un filo il disco
ed applichiamo una tensione al filo stesso.
Il disco, con il suo serbatoio di
anidride carbonica, accelererà,
fino a che verrà applicata la
tensione al filo, per poi muoversi
a velocità costante al cessare
della forza.
Richiami di Fisica Generale – Cinematica e Dinamica - 19
La Forza d’Inerzia (3)
Se seguiamo il fenomeno
mediante fotogrammi scattati
ad alta velocità possiamo
calcolarci il valore di Velocità
locale che, riportato su un
grafico temporale, mostra un
valore di accelerazione
costante pari a:
F
a=
m
Il Momento
Richiami di Fisica Generale – Cinematica e Dinamica - 20
G
Il Momento è una grandezza vettoriale pari al
prodotto vettoriale fra la forza ed il braccio.
L’unità di misura è: (N m)
Il momento richiede la presenza di un fulcro e di
una leva ed è l’espressione fisica di fenomeni
molto noti come la carrucola, la leva, gli arti umani,
ecc…..
G
G
M = F ×l
Esercizi (1)
Richiami di Fisica Generale – Cinematica e Dinamica - 21
1) Un aereo percorre, con moto uniforme, 700 km in 2
ore.Calcolare la sua velocità in km/h ed in m/s.
2) Quale distanza percorre in 1 minuto un’ autovettura
che viaggia a 100 km/h ?
3) Il rintocco di una campana segnala le ore 12:00. Se il
suono viaggia a 344 m/s a che ora un osservatore
posto a 1000 metri dalla campana avvertirà il
rintocco?
4) Un treno viaggia ad una velocità di 100 km/h per 2
ore, a 120 km/h per 1 ora e a 160 km/h per 0,5 ore.
Calcolare la sua velocità media.
Richiami di Fisica Generale – Cinematica e Dinamica - 22
Esercizi (2)
5) Calcolare la distribuzione di velocità e la velocità
media nel caso di un corpo che si sposti seguendo
una legge spazio-temporale come quella riportata in
tabella.
Tempo (s)
0
1
2
4
6
8
40
35
30
Posizione (m)
Distanza (m)
0
4
10
15
26
35
25
20
15
10
5
0
0
1
2
3
4
Tempo (s)
5
6
7
8
Esercizi (3)
Richiami di Fisica Generale – Cinematica e Dinamica - 23
6) Due auto hanno una velocità iniziale di 60 km/h e
100 km/h rispettivamente. A un certo istante
frenano contemporaneamente, la prima con una
accelerazione di -1,66 m/s2 e la seconda con -1,85
m/s2. Quale delle due auto si arresta per prima ?
7) Un oggetto si muove di moto uniformemente
accelerato con un’accelerazione di 5 m/s2. Sapendo
che la sua velocità iniziale è di 5 m/s, calcolare la
velocità istantanea e la distanza percorsa negli
istanti: 1 s, 2 s, e 5 s.
Richiami di Fisica Generale – Cinematica e Dinamica - 24
Esercizi (4)
8) Calcolare la forza agente su di un corpo di massa
pari a 12 kg quando è sottoposto ad un’accelerazione
di 3 m/s2.
9) Calcolare il momento esercitato da una forza di 50
kgf su un braccio di 30 cm.
10) Calcolare la forza necessaria a mantenere in
equilibrio il sistema sotto riportato; calcolare inoltre
la reazione vincolare del cuneo di supporto.
0,2 m
0,8 m
?
20 N
?
Esercizi (5)
Richiami di Fisica Generale – Cinematica e Dinamica - 25
10) Calcolare il lavoro fatto da una forza di 20 N
quando produce uno spostamento di 70 cm.
11) Calcolare il valore della forza che effettua un lavoro
di 68 Nm su di un corpo di massa pari a 20 kg che
striscia su di un piano orizzontale, coefficiente di
attrito radente pari a 0.693, per 0,5 m.
12) Un corpo di massa 30 kg viene lasciato cadere da
un’altezza di 10 metri; a quale velocità raggiungerà
il terreno ?
Richiami di Fisica Generale – Cinematica e Dinamica - 26
Esercizi (6)
13) Calcolare la velocità raggiunta dal corpo di massa pari
a 30 kg che scivola su di un piano inclinato, privo di
attrito, partendo da un’altezza h pari a 10 metri.
Considerare il corpo come puntiforme ed un angolo di
30° di inclinazione del piano.
mg senα
mg cosα
h
mg
α
14) Calcolare la velocità raggiunta dal corpo di massa pari
a 30 kg che rotola su di un piano inclinato, coefficiente
di attrito pari a 0.08, partendo da un’altezza h pari a
10 metri. Considerare il corpo come puntiforme ed il
piano inclinato a 30°.