Università degli Studi di Padova
Laurea in Tecnologie Forestali e Ambientali
Programma del corso di MATEMATICA A.A. 2013-2014
PRIMO COMPITINO
1. Richiami e insiemi numerici.
Insiemi e sottoinsiemi. Operazioni sugli insiemi. Relazioni tra insiemi. Classificazione
dei numeri. Definizione e proprietà dei numeri reali. Relazione d’ordine. Radicali.
Valore assoluto. Potenze. Il piano cartesiano, retta e parabola. Distanza tra due
punti nel piano. La circonferenza. Insiemi di numeri reali e loro proprietà; massimo,
minimo, estremo superiore, estremo inferiore.
2. Disequazioni.
Disequazioni di primo grado e di secondo grado. Disequazioni razionali. Sistemi di
disequazioni. Disequazioni con il modulo. Disequazioni irrazionali.
3. Funzioni.
Definizione di funzione di variabile reale. Dominio, codominio, immagine. Funzioni iniettive, surgettive. Funzioni pari e dispari. Funzioni monotone. Successioni
(cenni). Funzioni elementari e loro grafici: modulo, esponenziale, potenza, funzioni
trigonometriche (seno, coseno, tangente). Funzione inversa. Funzione logaritmo e inverse delle funzioni trigonometriche (arcoseno, arcocoseno, arcotangente). Funzione
composta. Massimo e minimo di una funzione.
4. Limiti.
Limiti di funzioni di variabile reale. Punto di accumulazione. Definizione di limite.
Interpretazione grafica del concetto di limite. Proprietà dei limiti. Operazioni sui
limiti. Limite della funzione composta.
n Forme indeterminate. Limiti di successioni.
sin x
exp(x) − 1
1
= e. lim
, lim
.
Alcuni limiti notevoli: lim 1 +
x→0
x→0
n→+∞
n
x
x
5. Derivate.
Funzione continua. Algebra delle funzioni continue. Teorema di Weierstrass. Teorema degli zeri. Teorema di tutti i valori. Definizione di derivata. Concetto geometrico
e fisico di derivata. Retta tangente e normale a una funzione in un punto. Derivata
delle funzioni elementari. Proprietà delle derivate. Derivata della somma, del prodotto, del quoziente, della composizione di funzioni. Teoremi del calcolo differenziale
(Rolle e Lagrange). Regola de l’Hôpital.
6. Studio di funzione.
Massimi e minimi relativi (o locali). Segno della derivata e monotonia della funzione
(crescenza e decrescenza). Concavità e convessità. Asintoti. Studio di una funzione e
grafico qualitativo. Problemi di massimo e minimo. Formula di Taylor e di McLaurin.
SECONDO COMPITINO
7. Integrazione.
Concetto di differenziale. Primitiva di una funzione. Integrale indefinito. Calcolo di
integrali indefiniti. Regola di integrazione per parti. Integrazione per sostituzione.
Integrazione di alcune funzioni razionali. Integrale definito. Teorema della media e
Teorema fondamentale del calcolo integrale. Calcolo di aree comprese tra due curve.
Calcolo di volumi. Integrali generalizzati. Esempi fisici.
8. Equazioni differenziali.
Soluzione di equazioni differenziali lineari e del I ordine, e lineari a coefficienti costanti
del II ordine. Equazioni differenziali a variabili separabili. Accenno all’equazione
nonlineare dell’accrescimento della popolazione.
9. Algebra lineare.
Vettori. Somma di vettori e prodotto per un numero reale. Prodotto scalare e
vettoriale. Prodotto misto. Significato geometrico del modulo del prodotto vettoriale
e del prodotto misto. Matrici e determinanti. Soluzione di sistemi lineari con il
metodo di eliminazione di Gauss. Numero di soluzioni di un sistema lineare: il
teorema di Rouché Capelli.
10. Metodi numerici.
Approssimazione ai minimi quadrati di dati sperimentali, calcolo della retta di regressione lineare. Il metodo dei trapezi per l’integrazione numerica.
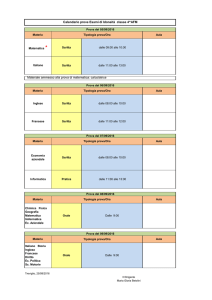
DATE DEI COMPITINI E DELLE PROVE DI ACCERTAMENTO
1o compitino 16/11/2013 ore 9.30 Aula Magna
2o compitino Data da definire
1a prova 29/01/2014 ore 9.30 aula 14P
1a registrazione 05/02/2014 ore 9.30 aula 4CG
2a prova 17/02/2014 ore 9.00 aula 10P e 1P
2a registrazione 24/02/2014 ore 9.30 aula 4CG
3a prova 18/06/2014 ore 9.00 aula 10P
3a registrazione 26/06/2014 ore 9.30 aula 4CG
4a prova 4/07/2014 ore 9.00 aula 10P
4a registrazione 11/07/2014 ore 9.30 aula 4CG
5a prova 12/09/2014 ore 9.30 aula 10P
5a registrazione 17/09/2014 ore 9.30 aula 4CG
BIBLIOGRAFIA
1. G. Artico. Istituzioni di Matematiche. Primo corso di matematica per la Laurea
triennale. Edizioni Libreria Progetto. Padova.
2. G. Artico. 333 esercizi svolti. Edizioni Libreria Progetto. Padova.
3. G. Artico. Richiami di matematica per l’accesso alle Facoltà scientifiche. Edizioni
Libreria Progetto. Padova.
DOCENTE RESPONSABILE DEL CORSO
Dott.ssa Ángeles Martı́nez Calomardo
Pagina web del docente: http://www.dmsa.unipd.it/~acalomar alla voce Didattica.
MATERIALE DIDATTICO
Materiale didattico disponibile sul sito Moodle della Scuola di Agraria e Veterinaria all’indirizzo https://elearning.unipd.it/scuolaamv/ (contattare il docente per la password di
iscrizione).
RICEVIMENTO
Il docente riceve gli studenti previo appuntamento per e-mail.
Ufficio del docente: Via Trieste 63, Terzo Piano della Torre Archimede, Stanza 311.
Previo accordo con gli studenti il docente potrà effettuare anche ricevimento in aula il
giovedı̀ mezz’ora prima della lezione.