UNIVERSITA’ DEGLI STUDI DI NAPOLI FEDERICO II
DIPARTIMENTO DI MATEMATICA E APPLICAZIONI RENATO CACCIOPPOLI
CORSO DI LAUREA IN MATEMATICA
ANNO ACCADEMICO 2013-2014
Sede del corso: Campus Universitario di Monte S. Angelo
www.dma.unina.it/~ccl
Obiettivi e finalità del Corso di Laurea
Il Corso di Studi in Matematica offre una solida preparazione di base per affrontare gli
studi successivi ed una formazione metodologica e flessibile finalizzata al Problem Solving
in
numerosi
campi
lavorativi
(ambito
industriale,
insegnamento,
ambito
economico/finanziario, ambito informatico, ricerca di base o applicata, e ovunque ci sono
problemi da risolvere)
Piu’ precisamente ha come obiettivo formativo la preparazione di laureati che:
possiedano adeguate conoscenze di base nell'area della Matematica, prevedendo
almeno una quota di attività formative caratterizzate da un particolare rigore logico e
da un elevato livello di astrazione;
possiedano competenze di calcolo numerico e simbolico e degli aspetti computazionali
della matematica e della statistica: In particolare abbiano acquisito capacità di
gestione e sviluppo di software matematico;
abbiano acquisito le metodiche disciplinari e siano in grado di comprendere e
utilizzare descrizioni e modelli matematici di fenomeni naturali, sociali ed economici, e
di problemi tecnologici;
siano capaci di lavorare in gruppo, di operare con definiti gradi di autonomia e di
inserirsi prontamente negli ambienti di lavoro, anche utilizzando una lingua dell’Unione
Europea diversa dall’italiano;
siano in grado di svolgere compiti tecnici o professionali definiti, ad esempio come
supporto modellistico-matematico e computazionale ad attività dell'industria, della
finanza, dei servizi e nella pubblica amministrazione, o nel campo dell'apprendimento
della matematica o della diffusione della cultura scientifica.
Ai fini indicati, in relazione a obiettivi specifici, saranno previste attività esterne, come
tirocini formativi presso aziende, strutture della pubblica amministrazione e laboratori, oltre
a soggiorni di studio presso altre università italiane ed estere, anche nel quadro di accordi
internazionali.
Requisiti di accesso
Per l’ammissione al Corso di Laurea, oltre alla capacità logico deduttiva, è richiesta allo
studente la predisposizione al rigore scientifico e la conoscenza di base degli argomenti
delle discipline scientifiche previsti dai programmi delle scuole medie superiori.
In particolare, le conoscenze richieste per l’accesso al Corso di Laurea previste
dall’Ordinamento Didattico, comprendono:
conoscenze di base di matematica, comprendenti i fondamenti del calcolo algebrico
ed aritmetico, della trigonometria, della geometria analitica, delle funzioni
elementari e dei logaritmi ;
conoscenze di base di fisica classica, con riferimento ai fondamenti della
meccanica, dell'ottica e dell'elettromagnetismo;
conoscenze basilari ed utilizzo dei principali programmi informatici di larga
diffusione;
conoscenze elementari della lingua inglese relativamente ai principi della traduzione
e comprensione di testi scritti semplici.
Inoltre sono richieste:
la capacità di interpretare il significato di un testo e di sintetizzarlo o di rielaborarlo
in forma scritta ed orale;
la capacità di risolvere un problema attraverso la corretta individuazione dei dati ed
il loro utilizzo nella forma più efficace;
la capacità di utilizzare le strutture logiche elementari (ad esempio, il significato di
implicazione, equivalenza, negazione di una frase, ecc.) in un discorso scritto e
orale,
la capacità di valutare criticamente un dato o un'osservazione e di utilizzarli
opportunamente nel loro contesto (es. saper cogliere una evidente incongruenza in
una misura scientifica).
Prima dell'inizio delle attività formative è prevista una prova di ammissione obbligatoria,
che ha lo scopo di fornire agli immatricolandi indicazioni generali sulle attitudini a
intraprendere gli studi prescelti e sulla padronanza delle conoscenze richieste per
l’accesso. I risultati della prova potranno evidenziare l'esistenza di carenze formative, da
colmare nel primo anno di corso. Il risultato della prova obbligatoria può comportare
l’obbligo di Obblighi Formativi Aggiuntivi (OFA).
Struttura del Corso di Laurea
Gli studi universitari adottano il sistema dei crediti. Con questo sistema l’attenzione si
sposta dall’insegnamento all’apprendimento, pesando i corsi universitari non in termini di
contenuti ma di lavoro richiesto allo studente. Il “Credito Formativo Universitario (CFU)” è
infatti la misura del lavoro di apprendimento - comprensivo di studio individuale, lezioni,
esercitazioni, etc. - necessario perché uno studente in possesso di un’adeguata
preparazione iniziale acquisisca conoscenze e abilità nelle attività formative universitarie.
La quantità di lavoro di apprendimento svolto in un anno da uno studente medio
impegnato a tempo pieno è convenzionalmente fissata in 60 crediti. Il numero di crediti da
acquisire per conseguire la laurea è pari a 180, equivalenti quindi a 3 anni. A 1 credito
formativo corrisponde un carico di 25 ore di lavoro complessivo per lo studente,
comprensivo del lavoro in aula e in laboratorio e dello studio individuale. Allo studio
individuale e’ dedicato almeno il 50% del tempo totale.
Ogni insegnamento è costituito da uno o più moduli. Per ogni insegnamento lo studente
supera un esame e riceve un voto espresso in trentesimi; contestualmente acquisisce i
crediti indicati per i moduli che costituiscono l’insegnamento. L’esame può svolgersi con
diverse modalità e potrà comprendere verifiche in itinere durante lo svolgimento del
modulo. Le informazioni relative a ciascun insegnamento sono raccolte in schede, una per
ciascun modulo, allegate al Regolamento didattico del Corso di Studio.
Il Percorso di Laurea
I ANNO: Valido per gli studenti immatricolati
nell’anno accademico 2013-2014
INSEGNAMENTO
CFU Moduli
Algebra 1
12 Unico
CFU/
modulo
13
s.s.d.
Tipologia
MAT02
Di Base
Geometria 1
12 Unico
12
MAT03
Di base
Analisi Matematica 1
13 Unico
13
MAT05
Di Base
Laboratorio di
Programmazione
Fisica 1 con Laboratorio
Laboratorio di Lingua
Straniera
TOTALE I ANNO
8
Unico
8
INF01
10 Unico
5 Unico
10
5
FIS01
6 Di Base
2 Affini/Integrativi
Di Base
Lingua Straniera
59
II ANNO: Valido per gli studenti immatricolati
nell’anno accademico 2012-2013
INSEGNAMENTO
CFU Moduli
Algebra 2
Geometria 2
Analisi Matematica 2
Fisica Matematica
Laboratorio di
Programmazione e Calcolo
6
9
9
9
9
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
CFU/
modulo
6
9
9
9
9
Probabilità e Statistica
Fisica 2 con Laboratorio
9
9
Modulo Unico
Modulo Unico
9
9
TOTALE II ANNO
60
s.s.d.
MAT02
MAT03
MAT05
MAT07
MAT08
Tipologia
Caratterizzante
Caratterizzante
Caratterizzante
Caratterizzante
9
Caratterizzanti
1 Di Base
MAT06
Di Base
FIS01- Affini/Integrativi
FIS08
III ANNO: Valido per gli studenti immatricolati
nell’anno accademico 2011-2012
INSEGNAMENTO
CFU Moduli
Fondamenti di Matematica
CFU/
modulo
10 Modulo Unico
10
Geometria 3
Sistemi Dinamici
6 Modulo Unico
14 2 moduli
6
7
Corso consentito o Affine
6
6
A scelta libera purché 12
coerenti con il progetto
formativo (art.10 comma
5a DM270/04). *
Attivita’ previste dall’art. 10 6
comma 5d DM 270/04 **
Seminario pre -laurea
2
Prova finale
4
TOTALE III ANNO
61
Modulo Unico
s.s.d.
Tipologia
MAT01 Caratterizzante
MAT04
MAT03 Caratterizzante
MAT05 Caratterizzante
MAT07
FIS01Affine/
FIS08;
Integrativa
INF01;
SECSS06
A Scelta
Altre attività
2
Altre attività
Prova Finale
* Gli studenti possono scegliere insegnamenti per 12 CFU
all’interno dell’allegato B3
tra gli insegnamenti caratterizzanti della laurea magistrale in matematica
presso altri corsi di laurea dell’ateneo purche’ coerenti con il percorso formativo
** ulteriori conoscenze linguistiche, nonché abilità informatiche e telematiche, relazionali, o
comunque utili per l'inserimento nel mondo del lavoro, nonché attività formative volte ad
agevolare le scelte professionali, mediante la conoscenza diretta del settore lavorativo cui
il titolo di studio può dare accesso, tra cui, in particolare, i tirocini formativi e di
orientamento.
Prossimamente
all’insegnamento
interessati a tale
scelta libera, un
l’Ateneo.
sara’ istituita dal ministero la Laurea Magistrale Abilitante
della Matematica e delle Scienze nella Scuola Media. Gli studenti
percorso sono fortemente consigliati di seguire, tra gli insegnamenti a
insegnamento di area Biologica, Chimica o Geologica attivati presso
Allegato B3: Insegnamenti a scelta dello studente.
INSEGNAMENTO
Moduli
CFU
s.s.d.
Teoria di Galois
Elementi di Geometria Algebrica e
Differenziale
Elementi di Topologia Algebrica e
Geometria Combinatoria
Elementi di Didattica della Matematica
Matematiche Complementari
Complementi di Analisi Matematica
Misura e Integrazione secondo
Lebesgue
Calcolo delle Probabilità
Statistica Matematica
Introduzione alla Fisica Matematica
del Continuo
Introduzione ai Metodi e Modelli
Matematici per le Applicazioni
Preparazione di esperienze didattiche
Modulo Unico
Modulo Unico
6
6
MAT02
MAT03
Modulo Unico
6
MAT03
Modulo Unico
Modulo Unico
Modulo Unico
Modulo Unico
6
6
6
6
MAT04
MAT04
MAT05
MAT05
Modulo Unico
Modulo Unico
Modulo Unico
6
6
6
MAT06
MAT06
MAT07
Modulo Unico
6
MAT07
Modulo Unico
6
Elementi di Fisica Moderna
Modulo Unico
6
Elementi di Economia Matematica
Laboratorio di Programmazione 2
Modulo Unico
Modulo Unico
6
6
FIS01FIS08
FIS01FIS08
SECS-S/06
INF01
Si tratta di un elenco di corsi da cui e’ possibile scegliere gli esami a scelta libera previsti
al terzo anno. Non essendo esami obbligatori non e’ garantita la loro attivazione tutti gli
anni.
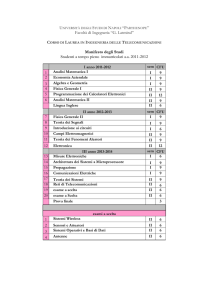
I corsi attivati nell’A.A. 2013/14
Per l'indicazione dell'aula e dei laboratori dove si svolgono lezioni ed esercitazioni e
per il relativo orario e’ possibile consultare il sito web del corso di Laurea.
Alcuni insegnamenti del primo e secondo anno possono essere sdoppiati in gruppi.
Per il primo anno (immatricolati 13/14) appartengono al primo gruppo gli studenti la
cui prima lettera del cognome e’ compresa tra A e I. Appartengono invece al
secondo gruppo gli studenti la cui prima lettera del cognome e’ compresa tra J e Z.
Per il secondo anno (immatricolati 12/13) appartengono al primo gruppo gli
studenti la cui matricola e’ pari. Appartengono invece al secondo gruppo gli studenti
la matricola e’ dispari
SSD
Insegnamento
Modulo Gruppo Docente Cognome
Docente
Nome
Sem.
MAT02
Algebra 1
unico
1
De Giovanni
Francesco
annuale
MAT02
Algebra 1
unico
2
Musella
Carmen
annuale
MAT03
Geometria 1
unico
1
Dragotti
Sara
annuale
MAT03
Geometria 1
unico
2
Olanda
Domenico
annuale
MAT05
Analisi
Matematica 1
unico
1
Sbordone
Carlo
annuale
MAT05
Analisi
Matematica 1
unico
2
Migliaccio
Lucia
annuale
FIS01
Fisica 1 con
Laboratorio
unico
Canale
Vincenzo
1
INF01
Laboratorio di
Programmazione
unico
1
Lapegna
Marco
2
INF01
Laboratorio di
Programmazione
unico
2
Simoncelli
Alba Chiara
2
MAT06
Probabilità e
Statistica
unico
Buonocore
Aniello
2
MAT02
Algebra 2
unico
1
Leone
Antonella
2
MAT02
Algebra 2
unico
2
Franciosi
Silvana
Barbara
2
MAT03
Geometria 2
unico
Durante
Nicola
1
MAT07
Fisica
Matematica
unico
1
Capone
Florinda
2
MAT07
Fisica
Matematica
unico
2
Grassini
Renato
2
MAT05
Analisi
Matematica 2
unico
1
Fusco
Nicola
1
MAT05
Analisi
Matematica 2
unico
2
Alvino
Angelo
1
MAT08
Laboratorio
Prog. e Calcolo
unico
1
Izzo
Giuseppe
1
MAT08
Laboratorio
Prog. e Calcolo
unico
2
Criscuolo
Giuliana
1
FIS01/08
Fisica 2 con
Laboratorio
unico
Balzano
Emilio
2
FIS01/08
Fisica 2 con
Laboratorio
unico
Festa
Gaetano
2
MAT01
MAT04
Fondamenti di
Matematica
unico
Tortora
Roberto
1
MAT05
Sistemi dinamici
1
Coti Zelati
Vittorio
1
MAT07
Sistemi Dinamici
2
Gentile
Maurizio
2
MAT03
Geometria 3
1
Lunardon
Gigliemo
2
MAT02
Teoria di Galois
unico
Franciosi
Silvana
Barbara
2
unico
TACE
unico
TACE
MAT03
MAT04
Elem. di geom.
Algebrica e
Differenziale
Elem. di
Didattica della
Matematica
MAT04
Matematiche
Complementari
unico
TACE
MAT05
Compl. di Analisi
Matematica
unico
Alvino
Angelo
2
MAT05
Misura e Integr.
secondo
Lebesgue
unico
Biacino
Loredana
2
MAT06
Calcolo delle
Probabilità
unico
Caputo
Luigia
1
MAT06
Statistica
Matematica
unico
Longobardi
Maria
2
unico
TACE
unico
TACE
MAT07
MAT07
Intr. Fisica
Matematica del
continuo
Intr. Metodi e
modelli mat. per
la applicaz.
FIS01/08
Prep. di
esperienze
didattiche
unico
Testa
Italo
2
FIS01/08
Elementi di
Fisica Moderna
unico
Peliti
Luca
2
unico
De Simone
Anna
2
Unico
TACE
SECS06
INF01
Elementi di
economia
matematica
Laboratorio di
Programmazione
2
Esame di Laurea
Lo studente può fare richiesta di tesi di laurea dopo aver acquisito almeno 150 CFU. Una
commissione apposita provvederà ad assegnare la tesi, sulla base delle richieste dello
studente e delle disponibilità dei docenti. Nel lavoro di Tesi lo studente viene seguito ed
indirizzato dal relatore. Prima della dicussione della tesi lo studente terrà un seminario sul
lavoro svolto, alla presenza del relatore e di un altro docente designato, tale seminario
comporta il conseguimento di 2 CFU. La tesi, discussa davanti alla commissione di
Laurea, consiste in una relazione scritta sul lavoro svolto e dà luogo all’acquisizione di 4
CFU.
Piani di studio
Il corso di laurea non prevede suddivisione in curricula, tuttavia, gli studenti potranno
presentare alla Segreteria studenti entro i tempi fissati dal Senato Accademico, piani di
studio individuali che saranno vagliati, sulla base della congruità con gli obiettivi formativi
specificati nell’Ordinamento didattico, dal Consiglio di Corso di Laurea .
UNIVERSITA’ DEGLI STUDI DI NAPOLI FEDERICO II
DIPARTIMENTO DI MATEMATICA E APPLICAZIONI RENATO CACCIOPPOLI
CORSO DI LAUREA MAGISTRALE IN MATEMATICA
ANNO ACCADEMICO 2013-2014
Sede del corso: Campus Universitario di Monte S. Angelo
www.dma.unina.it/~ccl
Obiettivi e finalità del Corso di Laurea
Il corso di Laurea specialistica in Matematica ha come obiettivo la formazione di una figura
professionale che, basandosi, in generale, su un’approfondita conoscenza del metodo
scientifico e, più in particolare, su una solida preparazione culturale nell’area della
Matematica, sia in grado di svolgere compiti di alta responsabilità in centri di ricerca, sia
pubblici che privati, nei servizi e nella pubblica amministrazione, anche in ambiti applicativi
scientifici, ambientali, sanitari, industriali, finanziari, nonché nel settore della
comunicazione della matematica e della scienza. A tal fine i laureati devono essere in
grado di analizzare problemi complessi, anche in contesti applicativi, e di fornire soluzioni
anche ricorrendo a sofisticate tecniche computazionali, probabilistico-statistiche ed
informatiche. Tale capacità di colloquiare con esperti di altri settori presuppone
competenze nel campo della comunicazione e della esemplificazione ed esposizione dei
problemi e dei metodi propri della disciplina. Devono essere inoltre in grado di utilizzare
fluentemente, in forma scritta ed orale, almeno una lingua dell’Unione Europea, oltre
l’Italiano, con particolare riferimento al lessico disciplinare. Devono infine avere capacità
decisionali ed essere capaci di lavorare con ampia autonomia.
Requisiti di ammissione
Per essere ammessi al corso di Laurea specialistica in Matematica occorre essere in
possesso della laurea o di altro titolo di studio conseguito all'estero, riconosciuto idoneo, e
possedere i requisiti richiesti dal regolamento didattico dell'Università degli Studi di Napoli
Federico II. Studenti in possesso di altre lauree di primo livello o di un coerente e congruo
numero di CFU potranno essere ammessi con un eventuale debito formativo determinato
attraverso la verifica dei requisiti curriculari e dell’adeguatezza della personale
preparazione secondo modalità definite dal Regolamento dell’ordinamento didattico. Le
modalità di ingresso al corso di laurea specialistica, compresa un’eventuale prova di
ammissione, sono definite nel Regolamento didattico. Piu’ precisamente
1) Studenti in possesso della Laurea in Matematica classe 32 ex D.M. 509/1999 e classe
2)
3)
4)
5)
L-35 ex D.M. 270/2004 della Facoltà di Scienze MM. FF. NN. dell’Università degli Studi
di Napoli Federico II, sono ammessi al Corso di Laurea Magistrale con il criterio del
silenzio-assenso. Il Consiglio di Coordinamento dei Corsi di Studi in Matematica può
comunque deliberare la non ammissione al corso di Laurea Magistrale con parere
motivato.
Studenti in possesso di lauree appartenenti alla classe L-35 (scienze matematiche) di
cui alla tabella allegata al D.M. 207/04, diverse dalla “Laurea in Matematica della
Facoltà di Scienze MM. FF. NN. dell’Università degli Studi di Napoli Federico II”, sono
ammessi previa delibera del Consiglio di Coordinamento dei Corsi di Studio in
Matematica, valutata la carriera scolastica.
Studenti in possesso di lauree non appartenenti alla classe L-35 (scienze
matematiche) di cui alla tabella allegata al D.M. 207/04, possono essere ammessi al
Corso di Laurea Magistrale purchè abbiano già conseguito l'equivalente di 110 CFU
nei SSD da MAT01 a MAT08. Il Consiglio di corsi di studi, valutata la carriera
scolastica, puo' inoltre richiedere l'iscrizione a singoli insegnamenti, prima
dell'iscrizione alla laurea magistrale, in maniera che sia assicurata una adeguata
conoscenza di base in tutti i settori scientifico disciplinari di area matematica presenti
nel regolamento della laurea triennale.
Il Consiglio di Coordinamento dei Corsi di Studio in Matematica potrà proporre anno
per anno altre modalità dell’eventuale prova di ammissione tendente ad accertare i
requisiti di cui al precedente comma 1. Tale modalità verrà inserita nel manifesto degli
studi e dovrà comunque prevedere l’analisi individuale della personale preparazione.
Al momento dell’iscrizione, gli studenti sono obbligati a scegliere un curriculum tra il
Curriculum Generale e il Curriculum Applicativo ,
Il Percorso di Laurea
I ANNO: Valido per gli studenti immatricolati
nell’anno accademico 2013-2014
Curriculum Generale
I ANNO
INSEGNAMENTO
Fondamenti di Analisi Superiore
CFU Mo CFU/
duli modulo
12
2
6
A scelta tra:
- Istituzioni di Algebra Superiore
- Istituzioni di Geometria
Superiore
A scelta tra gli insegnamenti attivati,
con i vincoli riportati in nota 1 , nota 2
e nota 3
A scelta tra gli insegnamenti attivati,
con i vincoli riportati in nota 1 , nota 2
e nota 3
12
2
6
24
4
6
12
2
6
TOTALE I ANNO
60
s.s.d.
Tipologia
MAT05
Caratterizzante
– formazione
teorica avanzata
MAT02 o Caratterizzante
MAT03
– formazione
teorica avanzata
Da MAT01 Caratterizzante
a MAT05
– formazione
teorica avanzata
Da MAT06 Caratterizzante
a MAT09
– formazione
applicativa
modellistica
Curriculum Applicativo
I ANNO
INSEGNAMENTO
CFU Mod CFU/
uli modulo
12
2
6
Fondamenti di Analisi Superiore
A scelta tra
- Fisica Matematica Superiore
- Processi Stocastici e
Applicazioni
- Calcolo Numerico e
Programmazione
A scelta tra gli insegnamenti attivati,
con i vincoli riportati in nota 1 , nota 2
e nota 3
A scelta tra gli insegnamenti attivati,
con i vincoli riportati in nota 1 , nota 2
e nota 3
12
2
6
12
2
6
24
4
6
TOTALE I ANNO
60
s.s.d.
Tipologia
MAT05
Caratterizzante
– formazione
teorica avanzata
MAT06 o Caratterizzante
MAT07 o
– formazione
MAT08
applicativa
modellistica
Da MAT01 Caratterizzante
a MAT05
– formazione
teorica avanzata
Da MAT06 Caratterizzante
a MAT09
– formazione
applicativa
modellistica
Corso di Laurea Magistrale in Matematica – Secondo Anno
Valido per gli studenti immatricolati
nell’anno accademico 2012-2013
(Unico per tutti i curricula)
II ANNO
INSEGNAMENTO
Attività affini o integrative (vedi
nota 2 e nota 3)
CFU Moduli
12
A scelta libera purché coerenti con 12
il progetto formativo (art.10 comma
5a DM270/04). (vedi nota 2)
Attivita’ previste dall’art. 10 comma 4
5d DM 270/04 (vedi nota 4)
Prova finale
32
TOTALE II ANNO
60
CFU/
s.s.d.
modulo
6/12 INF01, da
FIS01 a
FIS08,
SECS-S06
6/12
Tipologia
Affini o
integrative
A scelta
Altre attività
Prova finale
Nota 1: Gli studenti per il primo anno possono scegliere liberamente, nel rispetto delle
propedeuticità, insegnamenti all’interno degli allegati da B3/1 a B3/7 con il vincolo che gli
insegnamenti relativi ai 60 CFU caratterizzanti del primo anno devono essere scelti tra
quelli attivati in almeno 4 allegati distinti da B3/1 a B3/7
Nota 2: Il numero complessivo di esami relativi alle tipologie “Caratterizzanti”, “Affini o
integrative” e “A scelta” non può superare il numero di 12.
Nota 3: Gli studenti iscritti al secondo anno possono scegliere insegnamenti dei SSD
consentiti (INF01, da FIS01a FIS08, SECS S06) tra quelli attivati per il corrente a.a.
presenti nell’allegato B3/8. E’ consentito l’inserimento di corsi di tipo Affine al primo anno
del corso di laurea magistrale, limitatamente ad un solo insegnamento, fermo restando il
numero complessivo di 60 CFU da conseguire ogni anno, e fermo restando i vincoli sui
SSD consentiti.
Nota 4: ulteriori conoscenze linguistiche, nonché abilità informatiche e telematiche,
relazionali, o comunque utili per l'inserimento nel mondo del lavoro, nonché attività
formative volte ad agevolare le scelte professionali, mediante la conoscenza diretta del
settore lavorativo cui il titolo di studio può dare accesso, tra cui, in particolare, i tirocini
formativi e di orientamento.
ALLEGATO B3/1
(LOGICA MATEMATICA e MATEMATICHE COMPLEMENTARI)
INSEGNAMENTO
CFU
Moduli
CFU/
s.s.d. Tipologia
modulo
Logica Matematica
6
1
6
MAT01 Caratterizz
ante
Teoria degli Insiemi
6
1
6
MAT01 Caratterizz
ante
Didattica della Matematica
6
1
6
MAT04 Caratterizz
ante
Matematiche elementari dal punto di vista
6
1
6
MAT04 Caratterizz
superiore
ante
INSEGNAMENTO
ALLEGATO B3/2
(ALGEBRA)
CFU
Moduli
Istituzioni di Algebra Superiore
12
2
CFU/
modulo
6
Algebra Commutativa
6
1
6
Algebra Omologica
6
1
6
Metodi Algebrici in Crittografia
6
1
6
s.s.d.
Tipologia
MAT02 Caratterizz
ante
MAT02 Caratterizz
ante
MAT02 Caratterizz
ante
MAT02 Caratterizz
ante
ALLEGATO B3/3
(GEOMETRIA)
CFU
Moduli
INSEGNAMENTO
Istituzioni di Geometria Superiore
12
2
CFU/
modulo
6
Fondamenti di Geometria Differenziale
6
1
6
Fondamenti di Geometria Algebrica
6
1
6
Fondamenti di Topologia Algebrica
6
1
6
Fondamenti di Geometria Combinatoria
6
1
6
Geometria Algebrica Computazionale
6
1
6
Strutture Geometriche Combinatorie
6
1
6
Topologia Algebrica e Geometrica
6
1
6
INSEGNAMENTO
ALLEGATO B3/4
(ANALISI MATEMATICA)
CFU
Moduli
Fondamenti di Analisi Superiore
12
2
CFU/
modulo
6
Analisi Reale
6
1
6
Calcolo delle Variazioni
6
1
6
Analisi Funzionale
6
1
6
Equazioni Differenziali alle derivate
parziali
Complementi di Analisi Superiore
6
1
6
6
1
6
s.s.d.
Tipologia
MAT03 Caratterizz
ante
MAT03 Caratterizz
ante
MAT03 Caratterizz
ante
MAT03 Caratterizz
ante
MAT03 Caratterizz
ante
MAT03 Caratterizz
ante
MAT03 Caratterizz
ante
MAT03 Caratterizz
ante
s.s.d.
Tipologia
MAT05 Caratterizz
ante
MAT05 Caratterizz
ante
MAT05 Caratterizz
ante
MAT05 Caratterizz
ante
MAT05 Caratterizz
ante
MAT05 Caratterizz
ante
ALLEGATO B3/5
(PROBABILITA’ E STATISTICA MATEMATICA e RICERCA OPERATIVA)
INSEGNAMENTO
CFU
Moduli
CFU/
s.s.d. Tipologia
modulo
Ricerca Operativa
6
1
6
MAT09 Caratterizz
ante
Processi Stocastici e Applicazioni
12
2
6
MAT06 Caratterizz
ante
Ottimizzazione Combinatoria
6
1
6
MAT09 Caratterizz
ante
ALLEGATO B3/6
(FISICA MATEMATICA)
CFU Moduli
INSEGNAMENTO
Fisica Matematica Superiore
12
2
CFU/
modulo
6
Fluidodinamica
6
1
6
MAT07
Modelli Matematici per la Biologia e per
l’Ambiente
Metodi Geometrico - Differenziali in Fisica
Matematica
Processi Evolutivi in Fisica Matematica
6
1
6
MAT07
6
1
6
MAT07
6
1
6
MAT07
1
6
MAT07
Equazioni Integro-Differenziali nella Fisica
Matematica
6
ALLEGATO B3/7
(ANALISI NUMERICA)
CFU Moduli
INSEGNAMENTO
Calcolo Numerico e Programmazione
12
2
CFU/
modulo
6
Analisi Numerica 1
6
1
6
Analisi Numerica 2
6
1
6
Calcolo Numerico
6
1
6
1
6
Calcolo Parallelo e Distribuito
INSEGNAMENTO
Fisica Moderna
6
ALLEGATO B3/8
(INSEGNAMENTI AFFINI O INTEGRATIVI
CFU Moduli
CFU/
modulo
6
1
6
Complementi di Fisica
6
1
6
Elementi di Economia Matematica
6
1
6
Laboratorio di Programmazione 2
6
1
6
s.s.d.
Tipologia
MAT07
Caratterizz
ante
Caratterizz
ante
Caratterizz
ante
Caratterizz
ante
Caratterizz
ante
Caratterizz
ante
s.s.d. Tipologia
MAT08 Caratterizz
ante
MAT08 Caratterizz
ante
MAT08 Caratterizz
ante
MAT08 Caratterizz
ante
MAT08 Caratterizz
ante
s.s.d. Tipologia
FIS01FIS08
FIS01FIS08
SECS/
S06
INF01
Affine
Affine
Affine
Affine
I corsi attivati nell’A.A. 2012/13
Per l'indicazione dell'aula e dei laboratori dove si svolgono lezioni ed esercitazioni e per il
relativo orario e’ possibile consultare il sito web del corso di Laurea.
SSD
Insegnamento
Modulo
Gruppo
Docente
Cognome
Docente Nome
Sem.
MAT01
Logica Matematica
unico
Vaccaro
Virginia
1
MAT01
Teoria degli Insiemi
unico
Dardano
Ulderico
1
unico
Mellone
Maria
2
unico
Tortora
Roberto
2
MAT04
Didattica della
Matematica
Matematiche elementari
dal punto di vista
superiore
MAT02
Istituzioni di Algebra
Superiore
1
De Giovanni
Francesco
1
MAT02
Istituzioni di Algebra
Superiore
2
De Giovanni
Francesco
2
MAT02
Algebra Commutativa
unico
Cutolo
Giovanni
2
MAT02
Algebra Omologica
unico
TACE
MAT02
Metodi Algebrici in
Crittografia
unico
De Falco
Maria
2
MAT03
Istituzioni di Geometria
Superiore
1
Orecchia
Ferruccio
1
MAT03
Istituzioni di Geometria
Superiore
2
Orecchia
Ferruccio
2
MAT03
Fondamenti di
Geometria Differenziale
unico
TACE
MAT03
Fondamenti di
Geometria Algebrica
unico
Ilardi
Giovanna
2
MAT03
Fondamenti di Topologia
Algebrica
unico
Dragotti
Sara
1
MAT03
Fondamenti di
Geometria Combinatoria
unico
Durante
Nicola
2
MAT03
Geometria Algebrica
Computazionale
unico
Di Gennaro
Roberta
2
MAT03
Strutture Geometriche
Combinatorie
unico
TACE
MAT03
Topologia Algebrica e
Geometrica
unico
TACE
MAT04
2
MAT05
Fondamenti di Analisi
Superiore
1
Greco
Luigi
1
MAT05
Fondamenti di Analisi
Superiore
2
Greco
Luigi
2
MAT05
Analisi Reale
unico
Da definire
MAT05
Calcolo delle Variazioni
unico
Stroffolini
Bianca
2
MAT05
Analisi Funzionale
unico
Carbone
Luciano
2
MAT05
Equazioni Differenziali
alle derivate parziali
unico
Fusco
Nicola
1
MAT05
Complementi di Analisi
Superiore
unico
TACE
MAT09
Ricerca Operativa
unico
Festa
Paola
1
MAT06
Processi Stocastici con
Applicazioni
1
Pirozzi
Enrica
1
MAT06
Processi Stocastici con
Applicazioni
2
Enrica
2
MAT09
Ottimizzazione
Combinatoria
unico
Pirozzi
Mutuato da
Ottimiz.
Combinatoria
laurea magistr.
in informatica
2
MAT07
Fisica Matematica
Superiore
1
Visentin
Francesca
1
MAT07
Fisica Matematica
Superiore
2
Marasco
Addolorata
2
MAT07
Fluidodinamica
unico
Capone
Florinda
2
unico
Visentin
Francesca
1
unico
Grassini
Renato
1
unico
Buonomo
Bruno
2
unico
TACE
Giuliana
1
MAT07
MAT07
Modelli Matematici per la
Biologia e per l’Ambiente
Metodi Geom. Differenziali in Fisica
Matematica
MAT07
Processi Evolutivi in
Fisica Matematica
Equaz. IntegroDifferenziali nella Fisica
Matematica
MAT08
Calcolo Numerico e
Programmazione
1
MAT08
Calcolo Numerico e
Programmazione
2
MAT08
Calcolo Parallelo e
Distribuito
MAT08
Analisi Numerica 1
MAT07
Criscuolo
Gerardo
2
unico
Toraldo
mutuato da
Calcolo Parallelo
mod.A
laurea triennale
in informatica
1
unico
Messina
Eleonora
2
Cuomo
MAT08
Calcolo Numerico
unico
MAT08
Analisi Numerica 2
unico
Criscuolo
FIS0108
Fisica Moderna
unico
Da definire
FIS0108
Complementi di Fisica
unico
Garufi
Salvatore
2
Giuliana
2
2
Fabio
2
Esame di diploma di Laurea
La laurea magistrale in Matematica si consegue dopo aver superato una prova finale,
consistente nella discussione di una tesi specialistica su un argomento specifico
preventivamente concordato con almeno un relatore che supervisionerà l’attività nelle sue
diverse fasi. La discussione della tesi avviene alla presenza di una commissione nominata
dalle strutture didattiche e dà luogo all’acquisizione di 32 CFU. L’attività svolta nell’ambito
della tesi può essere effettuata sia nell’interno delle strutture universitarie, sia presso centri
di ricerca, aziende o enti esterni, secondo modalità stabilite dalla strutture didattiche.