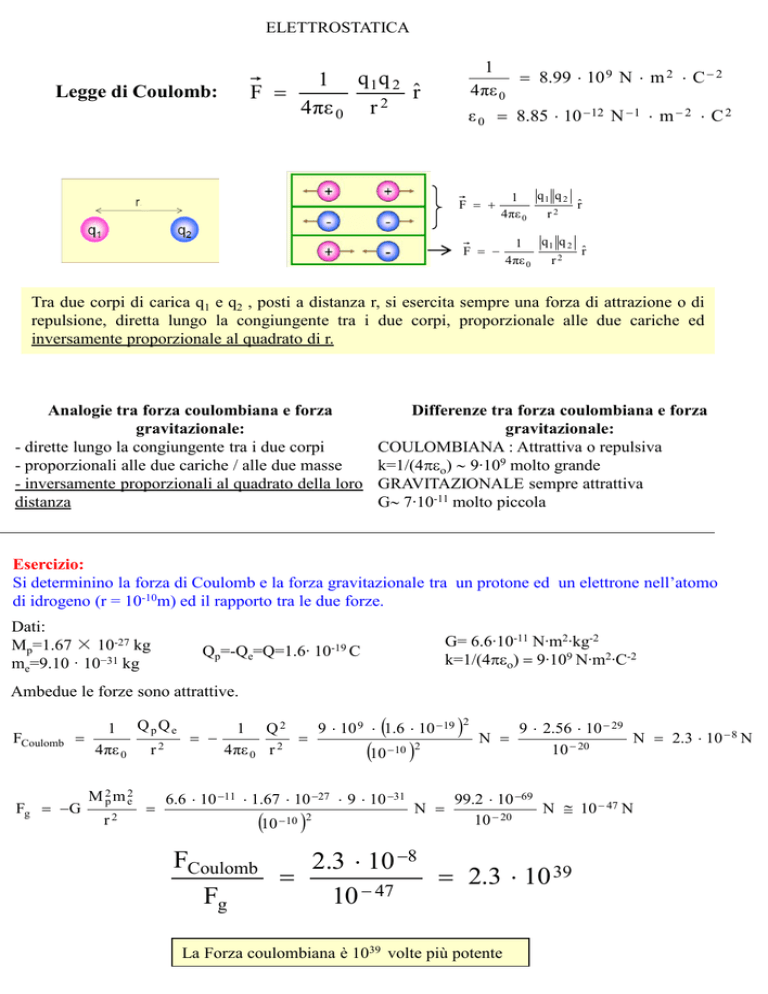
ELETTROSTATICA
Legge di Coulomb:
1 q 1q 2
F
r̂
4 πε 0 r 2
1
8.99 10 9 N m 2 C 2
4 πε 0
ε 0 8.85 10 12 N 1 m 2 C 2
F
1 q1 q 2
r̂
4 πε 0
r2
F
1 q1 q 2
r̂
4 πε 0
r2
Tra due corpi di carica q1 e q2 , posti a distanza r, si esercita sempre una forza di attrazione o di
repulsione, diretta lungo la congiungente tra i due corpi, proporzionale alle due cariche ed
inversamente proporzionale al quadrato di r.
Analogie tra forza coulombiana e forza
gravitazionale:
- dirette lungo la congiungente tra i due corpi
- proporzionali alle due cariche / alle due masse
- inversamente proporzionali al quadrato della loro
distanza
Differenze tra forza coulombiana e forza
gravitazionale:
COULOMBIANA : Attrattiva o repulsiva
k=1/(4 9∙109 molto grande
GRAVITAZIONALE sempre attrattiva
G 7∙10-11 molto piccola
Esercizio:
Si determinino la forza di Coulomb e la forza gravitazionale tra un protone ed un elettrone nell’atomo
di idrogeno (r = 10-10m) ed il rapporto tra le due forze.
Dati:
Mp=1.67 × 10-27 kg
me=9.10 · 10−31 kg
G= 6.6∙10-11 N∙m2∙kg-2
k=1/(49∙109 N∙m2∙C-2
Qp=-Qe=Q=1.6∙ 10-19 C
Ambedue le forze sono attrattive.
FCoulomb
Fg G
2
9 10 9 1.6 10 19
1 QpQe
1 Q2
9 2.56 10 29
N
N 2.3 10 8 N
2
2
2
20
10
4 πε 0 r
4 πε 0 r
10
10
M 2p m e2
r2
6.6 10 11 1.67 10 27 9 10 31
10 10 2
N
99.2 10 69
N 10 47 N
10 20
FCoulomb
2.3 10 8
2.3 10 39
47
Fg
10
La Forza coulombiana è 1039 volte più potente
Commenti sulla legge di Coulomb:
Vale il Principio di sovrapposizione:
Data una distribuzione di n cariche puntiformi, la forza risultante su ognuna di esse è pari alla
somma vettoriale delle forze dovute alle singole cariche.
Nuova unità SI: Coulomb (molto grande);
La carica elettrica si conserva (come la massa)
La carica elettrica è discreta (q = ± N e)
dove N= numero discreto (solitamente molto grande) ed e=carica dell’elettrone
qprotone=1.6∙10-19C=- qe=-e dove e<0 è una scelta fatta a priori
Tra due cariche q e Q poste a distanza r si esercita la forza:
F
1
Qq
rˆ
2
4 0 r
La carica Q crea attorno a se un:
F
E
q
Campo elettrico:
Campo vettoriale definito in un dato punto dello
spazio come la forza elettrica agente su una carica
positiva di prova q posta in quel punto diviso per il
valore della carica di prova stessa
Ogni altra carica q che si trova nella regione circostante Q risente di una forza di attrazione/repulsione
dovuta alla presenza della carica Q
Unità di misura del campo elettrico: N/C
a)
b)
Esempio:
Campi elettrici generati da:
a)una carica puntiformepositiva(linee di forza uscenti)
b)una carica puntiforme negativa(linee di forza entranti)
c)
c) più cariche puntiformi.
Vale il principio di sovrapposizione: Il campo generato da
due o più cariche puntiformi è uguale al vettore somma
dei campi elettrici di ognuna delle cariche prese
N
N
separatamente
Q
1
Etot E n
n 1
n
n 1 4 o r r
n
3
r rn
d) distribuzione continua di carica.
Vale il principio di sovrapposizione: Il campo generato da
due o più cariche puntiformi è uguale al vettore somma
dei campi elettrici di ognuna delle cariche prese
separatamente
E
1
4 0
lim
qi 0 i
qi
1
dq
ˆ
r
rˆ
i
2
2
4 0 r
ri
q
E
Esercizio:
Trovare il campo coulombiano nel punto P di coordinate (0,0,5cm) prodotte da due cariche puntiformi
di uguale valore, Q1 = Q2 = Q poste nei punti di coordinate (3cm,0,0) e (0,4cm,0).
r1 x1i y1 j z1k 3i
r2 x2i y2 j z2 k 4 j
r xi yj zk 5k
R1 r r1 3i 5 k
R2 r r2 4 j 5k
R1
3i 5 k
ˆ
R1
34
R1
R2
4 j 5k
ˆ
R2
41
R2
R1 9 25 34 5.8cm
R2 16 25 41 6.4cm
Rˆ1
Q
Q 3i 5 k
cm 2
2
32
4πε o R
4πε o
34
1
R2
Q
Q 4 j 5k
E2
cm 2
4πε o R 2
4πε o
413 2
E1
campo coulombiano nel punto P dovuto alla carica Q1
campo coulombiano nel punto Pdovuto alla carica Q2
2
Il campo coulombiano nel punto P generato dalle due cariche Q1 e Q2 è dato da:
Qn R n
Q 3i 5 k
4 j 5k 2
cm
3
4πε o
34 3 2
413 2
n 1
n 1 4πε o R
n
Q
Q
0.01i 0.02 k 0.01 j 0.02k cm 2
0.01i 0.01 ˆj 0.04kˆ cm 2
4πε o
4πε o
Etot
En E1 E2
2
2
Esercizio:
Due piccole sfere che portano le cariche Q1=7.00 mC e Q2=5.00 mC, distano 20.0 cm l'una dall'altra. Se
Q2 fosse libera di muoversi, quanto varrebbe la sua accelerazione, sapendo che la sferetta 2 ha una
massa di 15 g?
Le due sferette sentono una forza di mutua repulsione (cariche di stesso segno) pari alla forza
columbiana:
12
1 Q1Q 2
C2
2 2 7.00 5.00 10
FCoulomb
8
.
99
Nm
C
7.87 N
4 0 r 2
0.2 2 m 2
La sferetta 2 se fosse libera di muoversi avrebbe quindi un'accelerazione data da:
a2
FCoulomb
7.87 N
524,4 m s 2
3
m2
15 10 kg
Esercizio:
Una bacchetta di lunghezza 14.0 cm, uniformemente carica, è piegata a formare un semicerchio come in
figura. La bacchetta possiede una carica totale pari a -7.50 mC.
Determinare il modulo e la direzione del campo elettrico nel centro del semicerchio O.
y
Il punto O si trova a distanza R=L/ da qualsiasi punto della barretta.
Preso quindi un elemento dl della barretta a cui risulta associata
Una carica infinitesima dq il campo elettrico nel punto P
generato da tale carica infinitesima è:
dE
dq
4 πε o R 2
O
x
dq
L
4 πε o
π
2
dl
Se è la densità lineare di carica e quindi Q= L, l’elemento
infinitesimo di carica sarà dato da dq= dl, dove:
d
R
L’elemento infinitesimo di arco può essere riscritto come:
dl Rdθ
Il modulo del campo elettrico infinitesimo è quindi:
dE
Tale campo può essere scomposto nelle due componenti lungo x ed y:
λ
dq
L
4 πε o
π
2
L
dθ
π
L
4 πε o
π
2
dE x dE cos θ
dE y dE sin θ
Già ad intuito si può dire che la componente dEy si annullerà con quella del campo generato
dall’elemento dl simmetricamente opposto (rispetto all’asse x).
Comunque si può vedere analiticamente che la componente lungo l’asse y del campo generato dalla
Barretta risulta uguale a =0, infatti:
π
2
Ey
dE sin θdE
y
π
2
λ
L
π
L
4 πε o
π
2
sin θdθ
Q
4ε o L2
π
2
sin θdθ
π
2
Q
π 2
cos θ π 2 0
2
4ε o L
0
Il campo elettrico nel punto P generato dalla barretta è quindi lungo l’asse delle x ed è dato da:
Ex
Q
Q
7.50 10 6 C
π 2
sin
θ
21.6 10 6 N C 21.6 MN C
π 2
4ε o L2
2ε o L2
2 8,85 10 12 C 2 N m 2 0.14 2 m 2
2
E 21.6MN C î
Teorema di Gauss
Ricordando che:
Si definisce flusso del vettore v attraverso la superficie A il prodotto scalare
del vettore v per il vettore A (definito dal vettore di modulo A e direzione
normale uscente dalla superficie stessa) :
Φ v A v A vA cos θ
Il teorema di Gauss afferma che:
Il flusso del campo elettrico totale che attraversa una qualsiasi superficie chiusa non contenente cariche
è nullo.
Il flusso del campo elettrico totale che attraversa una qualsiasi superficie chiusa contenente una carica
Q
Q è pari a Q/o
Φ E A
In generale:
ΦE
εo
Q
E dA int
εo
Poichè il valore di non dipende dalla forma della superficie, il teorema di Gauss è molto utile per
determinare il campo elettrico generato da una densità di carica uniforme che abbia una qualche proprietà
di simmetria.
Esercizio:
Una ricercatrice sta lavorando a un esperimento di biologia e ha bisogno di creare un campo elettrico
di modulo 430 N/C a una distanza di 10 cm dal centro di una lastra quadrata conduttrice di lato 4.5m
da entrambe le parti. Qual’è la carica da mettere sopra la lastra?
La simmetria dello spazio è piana, scegliamo come superficie un cilindro di sezione S come in figura.
Il flusso lungo il mantello del cilindro è nullo in quanto data la distribuzione di carica lungo il piano, il
campo elettrico è nullo lungo la direzione parallela al piano stesso (per ragioni di simmetria il campo
elettrico è ortogonale alla lastra) . Inoltre, se supponiamo che la carica distribuita sia positiva le linee di
forza del campo saranno uscenti (entranti nel caso di carica negativa) su entrambe le facce della lastra.
Il flusso attraverso ciascuna base sarà quindi ES.
E E ( M ) E ( S1 ) E ( S 2 ) 2 E ( S ) 2 E nˆ S 2 ES
0
Per il teorema di gauss:
2 ES 2 EL2
E
Q
Q
E
0
quindi:
0
Q
2ε 0 L2
Il campo elettrico è uniforme,
non dipende cioè dalla distanza dalla piastra, e la carica che
bisogna mettere sopra la piastra per avere il campo elettrico E=430 N/C è:
S
1
Q 2 0 L E 2 8.85 10
2
12
N
1
m C 4.5 m 430 N C 154122.75 10
2
2
2
2
12
E
M
C 0.154 mC
S
1
CONDUTTORI in EQUILIBRIO ELETTROSTATICO
I conduttori sono materiali attraverso cui le cariche si muovono liberamente (nei metalli gli
elettroni di conduzione). Un conduttore si può caricare per contatto con un corpo carico
(acquista la stessa carica) o per induzione elettrostatica (acquista carica opposta) e si dice in
equilibrio elettrostatico quando tutte le cariche presenti in esso sono ferme.
Proprietà di un conduttore in equilibrio elettrostatico:
Il campo elettrico all’interno di un conduttore è nullo (le cariche non si devono muovere)
Qualunque eccesso di carica si distribuisce sulla superficie esterna
Il campo elettrico appena al di fuori del conduttore carico è perpendicolare alla superficie del
conduttore stesso ed ha intensità paria σ ε o dove è la densità superficiale di carica in quel punto
Se la forma del conduttore è irregolare le cariche tenderanno ad accumularsi sulle regioni con
raggio di curvatura minimo (punte)
Esercizio:
Determinare l’intensità del campo in prossimità di un conduttore sferico isolato di raggio ro e carica Q.
Noi sappiamo che per un conduttore in equilibrio elettrostatico il campo elettrico in
prossimità del conduttore è ortogonale alla superficie del conduttore stesso e pari a
E o
La densità superficiale di carica è pari alla carica per unità di superficie, cioè Q/S dove S per una sfera
è pari a 4ro2. Il campo elettrico sarà quindi:
E
Q
Q
o o S 4 o ro2
Come avremmo già potuto intuire. Il conduttore sferico si comporta come una superficie sferica
uniformemente carica (non una sfera uniformemente carica!!!!) per la quale il campo nella regione
interna alla superficie è nullo ed all’esterno è pari a
E
Q
4 o r 2
Esercizio:
Determinare il valore del campo elettrico E tra le armature di un condensatore, ciascuna delle quali ha
un’area A pari a 0.19 m2 e porta una carica di valore assoluto Q=1.3 mC
NB: nota sui condensatori:
Sono dispositivi costituiti da due conduttori tra loro isolati posti l'uno vicino all'altro in modo da poter
assumere che vi sia induzione totale. Un semplice tipo di condensatore è costituito da due lamine metalliche
piane e parallele poste ad una distanza molto piccola rispetto all’area delle loro superfici.
In condizioni normali sulle due lamine sono localizzate cariche uguali ed opposte.
E
La carica è distribuita in maniera uniforme a causa dell’attrazione esercitata dalla carica di
+
segno opposto presente sull’altra armatura; anche il campo è pressoché uniforme (ad
+
eccezione della regione dei bordi).
+
+
Poichè il campo è uniforme il suo modulo in tutta la regione tra le armature è uguale a
+
quello immediatamente nelle vicinanze di ciascuna armatura.
Sappiamo che per un conduttore carico in equilibrio elettrostatico E o
+
E
Q
1.3 10 6 C
0.77 10 6 N C
2
12
2
1 2
o o A 0.19m 8.85 10 C N m
ENERGIA POTENZIALE E POTENZIALE ELETTRICO
Una carica di prova q0 immersa in un campo elettrico E (generato da una distribuzione di carica) è
soggetta ad una forza F=q0E . Se una carica viene spostata il lavoro fatto dall'agente esterno è opposto
al lavoro del campo- Il lavoro del campo per uno spostamento infinitesimo è:
dL F d s q 0 E d s
Poiché la forza coulombiana è una forza conservativa il lavoro dipende solo dalle posizioni iniziali e
finali => si può definire un’energia potenziale coulombiana ( grandezza scalare)
La variazione di energia potenziale è pari al lavoro compiuto
dalla forza elettrica cambiato di segno :
U U b U a L F ds
b
a
Esempio:
Consideriamo il campo elettrico generato da una carica q puntiforme.
La variazione di energia potenziale di una carica di prova qo quando viene spostata da un punto a, posto
ad una distanza ra da q ad un punto b posto ad una distanza rb da q è:
qq
U b U a F ds o
4 o
1 rb
qo q
r r 4 o
a
rb
qo q
dr
r r 2 4 o
a
Che ci porta a dire che l’energia potenziale
ad una distanza r dalla carica q è:
U(r)
1 1
rb ra
qo q 1
4πε o r
Dove si è considerato che U(r→∞)=0, cioè l’energia potenziale è uguale a zero quando le due cariche
sono molto lontane tra loro tanto da poter trascurare l’interazione elettrostatica
Esempio:
Consideriamo il campo elettrico generato da un numero qualsiasi di cariche puntiformi.
Consideriamo prima che il campo sia generato da due cariche puntiformi e che una terza carica di prova
risenta di tale campo. La forza agente su questa carica è data, per il principio di sovrapposizione da:
F qo E qo E1 E2
Il lavoro compiuto da F quando la carica qo viene portata da a a b è:
L
b
a
F ds
b
a
b
b
qo E1 E2 ds qo E1 ds E2 ds L1 L2
a
a
Il lavoro fatto da F è pari alla somma dei lavori effettuati dai campo generati dalle singole particelle,
ciascuno indipendente dal cammino effettuato, quindi anche il lavoro compiuto da F è indipendente dal
cammino ed F è conservativa.
Ub Ua
b
a
b
b
q q
F ds qo E1 ds E2 ds o 1
a
4 o
a
1
1 qo q 2
r
r
1
b
1
a
4 o
1
1
r
r
2
b
2
a
Se prendiamo a come un punto all’infinito, r1a =r2a =∞, e chiamiamo r1 =r1b la distanza in un certo punto
della carica qo dalla carica q1 e r2=r2b la distanza sempre in quel punto dalla carica q2, l’energia
potenziale in quel punto, dovuta al campo elettrico totale sarà:
U
qo
4 o
q1
q
2
r2
r1
Energia potenziale di un campo
generato da due cariche puntiformi
U
Generalizzando
qo
4πε o
qi
ri
Energia potenziale di un campo
generato da un sistema di infinite
cariche puntiformi
POTENZIALE ELETTRICO:
V
U
qo
Unità di misura Volt=J/C=Nm/C
NB il campo elettrico sta alla forza F elettrica come il potenziale elettrico sta all’energia potenziale elettrica
Potenziale elettrico per un sistema di
infinite cariche puntiformi:
V
U
1 qo
qo
qo 4πε o
qi
1
r 4πε
i
o
qi
r
i
Esercizio:
Determinare il potenziale elettrico nel punto P in figura dove q1 = 33 nC, q2 = -51 nC e q3 = 47 nC.
1
V
4πεo
q
1
ri 4πε
i
o
P
r3
q3
33nC 51nC 47nC
r2
r3
r1
r2
9
51
47 10 C
33
V 8.99 109 Nm 2C 2
3 4.2 103V
93
93
92 2
10 m
r1
93 mm
q1
q2
93 mm
Esercizio:
Determinare il campo elettrico ed il potenziale elettrico nel punto al centro del quadrato disegnato in
figura, avente come vertici le quattro cariche:
Q1=Q2=Q3=Q4=5·10-10 C
Il campo elettrico generato da un numero discreto di cariche e
misurato in un punto P definito dal vettore posizione r, è dato
da:
Qn
1
Etot r En r
r
3 rn
4
n 1
n 1
o r rn
4
Q
Q2
1
4
Q
3
r
r
1
2
r
r
3
4
10cm
Q
4
Nel nostro caso, le cariche sono 4, tutte uguali, poste ai vertici di un quadrato ed il punto in cui si vuole
calcolare il campo è centro del quadrato che facciamo coincidere con l'origine del sistema di riferimento.
0
Si ha allora:
Q1 Q2 Q3 Q4 Q
4
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
rn
Q
Q r1 r2 r3 r4
Q r1 r2 rˆ1 rˆ2
Etot 0
0
r 0
2 4πε
2
2
4
πε
4
πε
r
n
1
o
o
o
2 2
2 2
n
r4 r1
r3 r2
r rn
2
per ogni n
2
Etot (0) 0
Il potenziale elettrico del campo generato dalle 4 cariche nel centro del quadrato è pari alla somma dei
potenziali elettrici in tale punto, dovuti ai campi elettrici generati dalle singole cariche (che nel nostro caso
particolare sono uguali)
V
1
4 o
Qi
r
i
4
Q 1
Q
2
1.41
4
4 9 109 Nm 2C 2 5 1010 C
4 63.6V 254 V
4 o r
4 o
0.1m
Esercizio:
Potenziale generato da un dipolo
Un dipolo è costituito da due cariche q di segno opposto ed uguali in modulo, poste ad una distanza d=2a tra
loro per le quali si trova che.
1) Il campo elettrico dovuto al dipolo su un punto posto sull’asse perpendicolare la congiungente le due
cariche (asse del dipolo) e passante per il centro di tale congiungente ad una distanza y dal centro del sistema
E
è diretto parallelamente all'asse del dipolo e ha modulo pari a:
E
1
qd
32
4 o y a 2
2
y a
E
1 qd
4 o y 3
y
-q
+q
d=2a
2) Il campo elettrico dovuto al dipolo su un punto posto lungo l’asse del dipolo ad una distanza z dal
centro della congiungente le due cariche è pari a
z
E
1 qdx
1 p
-q
E
+q
3
3
4 o z
4 o z
d=2a
Dove p qdx
detto momento del dipolo è un vettore che ha per modulo il
prodotto della singola carica per la distanza tra le due cariche ed è
diretto lungo la congiungente le due cariche nella direzione che va
dalla carica negativa a quella positiva
Esercizio:
In figura è rappresentato un dipolo di momento
z
p qdk
posto nell’origine degli assi. Determinare il potenziale prodotto dal dipolo a
distanze molto maggiori della distanza d tra le cariche +q e –q.
r+
+
r
Indichiamo con V+ e V- i contributi al potenziale dovuti rispettivamente
alla carica +q ed alla carica –q.
Si ha:
V V V
q
q
q 1 1
q r r
4 o r 4 o r 4 o r r 4 o r r
P
ry
x
-
Se r>>d => r+ r- r, in un’approssimazione per cui r+ , r- ed r sono praticamente paralleli
p
(vedi figura sotto) per cui:
r+
d cos
p cos
p rˆ
V
4 o
r2
4 o r 2
4 o r 2
q
r
+
Dove è l’angolo tra r e all’asse del dipolo
-
r r
r-
r r d cos
Il potenziale è nullo in tutti i punti del piano xy ( per i quali = 90°),
È positivo in tutti i punti al di sopra del piano xy (0°< < 90°),
È negativo in tutti i punti al di sotto del piano xy (90°< < 180°),
Diminuisce come 1/r2 lungo qualunque direzione radiale (dove però r >> d)
POTENZIALE PRODOTTO DA UNA DISTRIBUZIONE CONTINUA DI CARICHE
N
qi
1
1
V
lim
4πεo Nq0 i 1 ri
4πεo
dq
r
i
dq = carica infinitesima ed r= distanza di dq dal punto P in cui si valuta il potenziale
Esercizio:
Sia data una barretta AB di lunghezza L, elettricamente carica con densità di carica lineare
uniforme.Determinare il potenziale V in un punto P lungo l’asse della barretta, a distanza d
r
dall’estremo A
x=0
P
d
A
x
x=L
B
+++++++++++++++++++
L
dx
NB: densità di carica lineare = Q/L ( carica per unità di lunghezza)
Consideriamo l’elemento di carica infinitesima dq sulla barretta AB posto ad una distanza x
dal punto A.
dq = dx,
Il contributo al potenziale in P dato da questo elemento è: dV 1 dq 1 λdx
4πεo r
4πεo r
Dove r = d+x, con 0< x <L, è la distanza dell’elemento dq da P.
Per il principio di sovrapposizione si ha:
1
V(P)
4πεo
B
λdx
λ
A r 4πεo
dx
λ
λ
xL
Ld
ln
x
d
ln
0 x d 4πεo
x 0
4πεo d
L
NB: Il potenziale calcolato in un punto P (con la posizione di riferimento in un punto a grande distanza
per cui V(∞)=0), ed il campo elettrico sono legati dalla relazione:
V E dr
P
Il potenziale elettrico è pari all’opposto dell’integrale di linea del
campo elettrico che va dalla posizione di riferimento all'infinito al
punto P in cui si valuta il potenziale stesso
Es: Potenziale elettrico in campo generato da una carica puntiforme, valutato in un punto P a distanza r
dalla carica:
r
r
r
Q
1
Q 1
Q 1
V E dr ' E dr'
d
r
4πε0 r 2
4πε0 r 4πε0 r
P
DIFFERENZA DI POTENZIALE
NB la scelta della posizione di riferimento è arbitraria, si può scegliere per esempio r=∞, o, come
spesso conviene fare quando si studiano dei circuiti elettrici, la “terra”.
Questo perché solo una variazione di energia potenziale ha un senso fisico e corrispondentemente una
variazione di potenziale cioè la “DIFFERENZA DI POTENZIALE” o “tensione elettrica”
U U b U a
Variazione di energia potenziale elettrica di una particella
prova con carica qo quando viene spostata da un punto a ad
un punto b
ΔV Vb Va
Ub U a
qo
Differenza di potenziale tra i punti a e b.
NB: qo deve essere piccola poichè si trascura il suo contributo al campo elettrico
ΔV Vb Va E d
b
a
L’integrale non dipende dal
cammino
Esempio:
Differenza di potenziale tra due punti a e b in un campo elettrico uniforme diretto lungo x
E E iˆ
d dx iˆ
campo elettrico uniforme diretto lungo x
y
a
spostamento lungo x
E
xb
xb
ˆ
ˆ
Vb Va E d E i i dx E dx E xb xa
xa
b
xa
x
V Ex
Se V0 rappresenta il potenziale dei punti sul piano yz (x=0) e V(x) è il potenziale dei
punti giacenti sul piano parallelo al piano yz posto a distanza d da quest’ultimo si ha:
V d Vo Ed
Si ha quindi che in un campo uniforme la differenza di potenziale varia linearmente
con x e decresce nella direzione del campo (analogo del potenziale gravitazionale in
prossimità della terra, dove il campo è in prima approssimazione uniforme e l’energia
potenziale rispetto al piano di rifermento (es: pavimento) aumenta linearmente con
l’aumentare dell’altezza h => U=mgh.
Esercizio:
Sia dato il condensatore piano in figura.
Tracciare un grafico della differenza di potenziale V(x)-V0 nella regione compresa tra le
armature e determinare la V tra le armature stesse. Si consideri che le dimensioni delle due
armature sia molto maggiore della loro distanza d =0.50 mm.
Il valore assoluto della densità superficiale di carica su ciascuna armatura è: 1.8 mC m2
Dimensioni delle armature >>d => campo elettrico uniforme
y
-
E
+
+
+
+
+
+
x
L’asse x passa per il centro del condensatore
La distribuzione di carica negativa coincide con il piano yz (x=0)
La distribuzione di carica positiva coincide con il piano x=d (parallelo
a yz).
E è rivolto lungo –x.
d
E
Sappiamo che il campo elettrico tra le armature di un condensatore piano vale:
Quindi:
E Eiˆ iˆ
o
σ
εo
Il potenziale elettrico sarà quindi:
1.8 106 C m 2
V x V0 Ex
x
x 2.0 105 N C x
12
2
2
o
8,85 10 C Nm
V x V0 a x
Cioè, nel piano x-V l'andamento di V(x)-V0 è rappresentato da una retta passante per
l’origine e di coefficiente angolare a2.0∙105 N/C
E
V(x)-Vo
Per disegnare il grafico mi calcolo il valore di V(x)-V0
alla distanza x = d = 0.5 mm, mi trovo il punto sul
piano ed unisco tale punto con l'origine degli assi per
ottenere la retta V(x)-V0=ax. Contemporaneamente
rispondo alla seconda domanda
100
50
0.25
0.5
x (mm)
V V (d ) V0 2.0 105 N C d 2.0 105 N C 0.5 103 m 100 V
Esercizio sul calcolo della velocità di una carica sottoposta ad un campo elettrico
Esercizio:
Cannone elettronico in un tubo catodico.
Le placche cariche del cannone elettronico di un tubo catodico sono chiamate anodo e catodo.
Gli elettroni vengono emessi dal catodo con velocità quasi nulla ed accelerati verso l’anodo che si trova
ad un potenziale positivo rispetto al catodo.
Alcuni degli elettroni escono attraverso un piccolo foro praticato al centro dell’anodo e formano il fascio
elettronico.
Supponiamo che la ddp (differenza di potenziale) anodo-catodo sia: V=VA-VC=2500V.
Ammettendo che gli elettroni partano da fermi, determinare:
a)L’energia cinetica degli elettroni all’uscita dall’anodo
b)La velocità degli elettroni all’uscita dall’anodo
A
C
2500 V
a) Per determinare l’energia cinetica degli elettroni all’uscita dell’anodo bisogna applicare la
conservazione dell’energia meccanica:
U c Tc U A TA Emeccanica
Dove:
• UC e TC=0 (velocità nulla) sono rispettivamente l’energia potenziale elettrica e l’energia cinetica
dell’elettrone quando si trova sul catodo
•UA e TA sono rispettivamente l’energia potenziale elettrica e l’energia cinetica dell’elettrone quando
si trova sull’anodo
U A U c TC TA TA TA U C U A
Ricordando che V=U/q dove q nel nostro caso è la carica dell’elettrone si può scrivere:
TA U C U A (e)VC (e)VA eVA VC
TA eV e2500 V 2500 eV 2.5 keV
NB: l’unità di misura eV, o elettronvolt è definita come l’energia acquisita da un elettrone
libero che attraversa una differenza di potenziale elettrico di 1 volt nel vuoto.
1 eV = 1,60 × 10-19 J;
b) La velocità dell’elettrone all’uscita dall’anodo è quindi:
vA
2TA
me
2eΔΔ
me
2 1.6 10 19 C 2.5 kV
9.1 10-31 kg
0.9 1015 m 2 s 2 3 107 m s
NB: Ogni punto della superficie di un conduttore carico in equilibrio elettrostatico si
trova allo stesso potenziale elettrico, cioè è una superficie EQUIPOTENZIALE.
Inoltre, poiché il campo elettrico all’intero del conduttore è nullo, il potenziale all’interno
del conduttore e uguale in ogni punto e pari al suo valore sulla superficie.
Esercizio:
Calcolare il potenziale di una sfera metallica piena isolata di raggio r0 = 0.1 m e
carica Q = 100 nC.
Su una sfera la carica si distribuisce uniformemente, essendo un conduttore in equilibrio
elettrostatico il campo elettrico all’interno della sfera è nullo mentre sulla superficie è
perpendicolare alla superficie stessa e vale:
E
Q
E
o 4 o ro2
A distanze r maggiori di r0 il campo elettrico è uguale a quello
generato da una carica puntiforme Q posta nel centro della
sfera, cioè è diretto radialmente con centro il centro della sfera
Q
e vale:
E
Q
Q
4 πε o r 2
4 r
2
o 0
4πεo r 2
Il grafico di E in funzione di r è rappresentato in figura:
r0
r
Per quanto riguarda il potenziale, esso all’interno della sfera è costante in ogni punto (in quanto E≡0)(
ricordiamo che E = - dV/dr, per cui se E≡0 V è costante), ed il suo valore è quello che assume sulla
superficie della sfera stessa. Poiché la carica Q si distribuisce uniformemente sulla superficie della sfera:
1
V(r0 )
4πεo
σ 4π r02
dq
1
σ
Q
σdS
dS
r0 4πεo r0
4πεo r0
4πεo r0
4πεo r0
9
Q
9
2
2 100 10 C
V (ro )
9 10 Nm C
9000 V
4 o r0
0.1 m
Potenziale sulla superficie della sfera
e all'interno di essa
Il potenziale in un punto P ad una distanza r>r0 dal centro della sfera (fuori dalla sfera) sarà dato da:
P
r
Q
V (r ) E d E dr
4 o
dr
Q
r 2 4 o r
r
Quindi ricapitolando, per una sfera conduttrice
in equilibrio elettrostatico :
E è nullo all’interno della sfera
Q
E è pari a 4πε r 2 sulla superficie della sfera
o o
Q
E è pari a
ad una distanza r >ro dal centro della sfera
4 πε o r 2
Q
Il potenziale V della sfera vale:
4 πε o ro
Q
Fuori dalla sfera il potenziale decresce con r come: 4 πε r
o
V
Q
4 πε o ro
Q
4 πε o r
r0
r
CONDENSATORI E CAPACITÀ
Il valore del potenziale elettrostatico di un conduttore isolato è proporzionale alla carica del conduttore e la
costante di proporzionalità C tra la carica ed il suo potenziale elettrostatico V riferito all’infinito viene
detta CAPACITÀ elettrica di un conduttore.
Q CV
C
Q
V
Unità di misura della
capacità:
faraday=F=C2/(Nm)
NB: La capacità dipende solo dalla forma del conduttore per cui possiamo associare ad un conduttore
una sua capacità specifica anche se in quel momento il conduttore è scarico.
Esempio:
Determinare la capacità di una sfera di raggio R
Sappiamo che per una sfera conduttrice di raggio R e carica Q il potenziale elettrostatico della sfera, rispetto
al riferimento all’infinito è dato da:
V
Q
C
4 o R
Q
Q
4 o R
V Q 4 o R
capacità di una
sfera di raggio R
CONDENSATORE:
Dispositivo costituito da due conduttori (armature) tra loro isolati posti l’uno molto vicino all’altro in
modo da poter assumere che vi sia induzione totale che viene usato nei circuiti per immagazzinare
carica ed energia elettrostatica.
Le due armature sono solitamente separate da un isolante (dielettrico).
La capacità C di un condensatore è data dal rapporto tra la carica accumulata sulle due armature e la
differenza di potenziale sulle due armature stesse.
Q
C
V
NB: La capacità dipende solo dalle caratteristiche geometriche del condensatore e dalla
del dielettrico interposto tra le sue armature.
Esempio:
A o
Capacità di un condensatore piano con il vuoto tra le due armature: C
d
0 A
Q
A
A
A=area delle due armature
C
V
Ed 0 d
d
d= distanza tra le due armature
natura
+
+
+
+
+
+
d
Esercizio:
Qual’è la capacità di un condensatore piano le cui armature sono quadrati di lato 122 mm, distanti 0.24
mm, fra i quali c’è il vuoto?
Qual’è la carica presente su questo condensatore se la ddp tra le armature è di 45 V?
0.122 m 8.85 1012 C 2 Nm2 1.32 1013 C 2 Nm 0.55 109 F 0.55 nF 550 pF
A
C o
d
0.24 103 m
2.4 103 m
2
Q CV 550 pF 45V 0.55 109 C 2 Nm 45 Nm C 25nC
Esercizio:
Determinare la capacità di un tratto di cavo coassiale di lunghezza L, supponendo che tra il filo interno e
l’armatura esterna vi sia il vuoto.
NB: Un cavo coassiale (come quello dell’antenna TV) è costituito da un filo conduttore circondato da un
cilindro conduttore coassiale fra i quali vi è interposto un isolante. É quindi un caso di condensatore
cilindrico ed ha una sua capacità.
Il filo metallico= armatura positiva +Q
Cilindro esterno= armatura negativa -Q
Per poter applicare la relazione C=Q/V
dobbiamo conoscere la ddp tra le armature di
un condensatore cilindrico di lunghezza L
molto maggiore della distanza tra le due
armature.
Ra
Rb
Il campo elettrico tra le due
armature di un condensatore
cilindrico con densità lineare
di carica =Q/L, è dato da:
E
Q=λL
Vb Va E d
a
b
Ra Er dr 2 o
Rb
2 o r
R Q L Rb
dr
ln b
ln
r
2
R
2
R
o
o
a
a
Ra
Rb
La capacità di un condensatore cilindrico, ed in particolare di un cavo coassiale (con isolante
il vuoto) di lunghezza L è quindi:
C
Q
V
Q
Rb
Q L
ln
R
2 o
a
2 o L
ln Rb Ra
La capacità di un condensatore cilindrico dipende dalla lunghezza dei cilindri e dal rapporto dei loro
raggi
Esercizio:
Supponiamo di voler costruire un condensatore piano con capacità pari ad 1F nel quale la distanza tra le
due armature è 10mm. Se le armature sono quadrate e tra loro c’è il vuoto quale deve essere la lunghezza
del loro lato?
2
C
A o
Cd
1F 10 m
1 C Nm m
A
1.12 109 m 2
12
2
10
2
2
d
o 8.85 10 C Nm 8.85 10 C Nm
L
A
1.12 109 m 34 km
CONDENSATORI IN SERIE ED IN PARALLELO
La capacità equivalente di un sistema di condensatori è la capacità di un unico condensatore che,
quando viene usato in luogo del sistema ha lo stesso effetto esterno.
1
C eq
capacità equivalente di N condensatori in SERIE:
N
i 1
1
Ci
C1 C2 C3
Ceq
CN
C1
N
C eq
capacità equivalente di N condensatori in PARALLELO:
C
C2
Ceq
C3
i
i 1
CN
Esercizio:
Si consideri il sistema di condensatori in figura, dove C1=2.9 μF, C2=1.8 μF, C1=2.4 μF.
La differenza di potenziale ai capi del sistema è Vb-Va=V=53 V.
a
-Q3
Si determinino:
C3
+Q3
a)La capacità equivalente C123 dell’intero sistema
-Q1
b)La ddp ai capi di ciascun condensatore
C1
c)La carica di ciascun condensatore
+Q
-Q2
C2
+Q2
1
I condensatori 1 e 2 sono in parallelo, questi possono essere sostituiti da un singolo
condensatore di capacità C12 data da: C12 C1 C 2 4.7 μF
C12
Q12 Q1 Q 2 Q1 Q 2 Q1 Q 2 Q1 Q 2
V12 V1 V2 V1 V1
V1
V12
b
-Q3
C3
+Q3
-(Q1+Q2)
Q12 Q1 Q 2
C12
-(Q1+Q2)
Il condensatore equivalente al sistema 1-2 è posto in serie con il condensatore 3. Questo sistema può
Essere sostituiro da un singolo condensatore di capacità:
1
a)
C123
C C12
C12 C 3
1
1
4.7 2.4
11.28
3
C123
μF
μF 1.6 μF
C12
C3
C12 C 3
C 3 C12
4.7 2.4
7.1
-Q = -Q3
Q = Q3
C123
Poichè i condensatori 1 e 2 sono in parallelo, questi due elementi ed anche il condensatore
equivalente 12 avranno ai loro capi la stessa ddp: V12=V1=V2
Poichè il condensatore 3 è in serie con il condensatre 12, la ddp V3 sommata a quella del sistema 12, V1,
deve essere uguale alla ddp totale V:
V V1 V3
Per determinare V1 e V3 occorre prima considerare le cariche presenti sulle armature
Dalla figura si desume che il condensatore 3 deve possedere una carica uguale ed opposta alla
somma delle cariche sulle armature di 1 e 2: Q 3 Q1 Q 2
Il condensatore equivalente 123 possiede questa stessa carica quando ai suoi capi è applicata la ddp V
C123
Q3
Q Q2
1
V
V
Q 3 C123 V 1.6μF 53V 85μC
V2 V1 V V3 53 35V 18 V
V3
Q3
85
V 35V
C3
2.4
Q1 C1 V1 2.9 18 mC 52 mC
Q C V 1.8 18 mC 32 mC
2 2
2
Q 3 85mC
DIELETTRICI
Quando un isolante o dielettrico viene posto in un campo elettrico, gli atomi e le molecole che lo
costituiscono si polarizzano e viene indotta una densità superficiale di carica legata. Questa densità di carica
legata, o polarizzazione, produce un campo elettrico che si oppone al campo esterno (verso opposto)
cosicché sia E che V si riducono. L’entità della polarizzazione è caratterizzata dalla costante dielettrica
relativa (al vuoto) k
Se consideriamo un condensatore per il quale, tra le due armature viene
posto una sostanza dielettrica, la costante dielettrica relativa di questo
isolante è pari al rapporto tra la ddp tra le armature quando tra di esse
c’è il vuoto e quella quando il condensatore è riempito con il dielettrico:
k
V0
V
Poiché k è sempre maggiore di 1 (k per il vuoto è 1), l’inserimento del dielettrico produrrà un
aumento della capacità del condensatore. Se C è la capacità in presenza del dielettrico e C0 quella
del condensatore quando tra le due armature vi è il vuoto si trova che:
k 1
Q
Q
Q
C
k
kC 0
V V0 k
V0
C kC 0
L’inserimento di un dielettrico fa aumentare la
capacità del condensatore di un fattore k
NB in finale si può scrivere:
k
E 0 V0
C
E
V C 0
Esercizio:
Un condensatore piano è costruito inserendo a sandwich un foglio di carta (k=3,7) di spessore 0.14
mm tra due fogli di alluminio di dimensioni 15 mm x 480 mm. Si determinino:
a)La capacità del condensatore
b)La massima differenza di potenziale che può essere applicata tra le due armature senza che si
verifichi la perforazione (rigidità della carta= 1.6•106 V/m). Si trascurino gli effetti di bordo
0A
1.5 4.80 10
3.7
3
m 2 8.85 10 12 C 2 Nm 2
168 10 11 F 1.7 nF
4
1.4 10 m
a)
C kC 0 k
a)
La rigidità dielettrica è il valore massimo di campo elettrico Emax che può essere presente nel
dielettrico senza che avvenga una scarica (cioè quando il materiale comincia a condurre)
d
Per un condensatore piano:
V E d 1.6 10 7 V m 1.4 10 4 m 2.24 kV
CORRENTE ELETTRICA
Il flusso della carica attraverso un elemento di circuito è
caratterizzato dall’intensità della corrente elettrica
I
Unità di misura
ampere 1A=1C/s
dQ
dt
Il senso della corrente corrisponde alla direzione della velocità di deriva vd dei portatori di carica positiva.
I nqv d A
La corrente in un conduttore viene espressa in termini
del moto dei portatori di carica:
Dove: n è la densità dei portatori di carica, q è la loro carica, vd la loro velocità di deriva, A la sezione
del conduttore
Legge di Ohm
ΔV Unità di misura Ohm
La resistenza R di un conduttore è definita come il rapporto tra la
R
1Ω=1V/A
differenza di potenziale ai capi del conduttore e l’intensità di corrente
I
La resistenza di un conduttore dipende dalla natura (resistività) e dalla forma geometrica del
conduttore stesso.
Se il conduttore ha una sezione uniforme di area A, lunghezza ℓ e resistività ρ la resistenza è data
dalla relazione:
R ρ
A
NB: la resistività di un conduttore varia con la temperatura, es: i materiali superconduttori hanno
resistenze bassime , ma solo per temperature molto basse, prossime allo zero assoluto
ρ= ρo[1+α(T-To)]
Dove α è il coefficiente termico e ρo è la resistività
alla temperatura di riferimento To
Gli elettroni, in assenza di campo hanno velocità in media nulla. Applicando un campo elettrico gli
elettroni si muovono con una velocità di deriva media vd opposta alla direzione del campo elettrico.
Se ai capi del conduttore viene mantenuta una ddp ΔV, la potenza, o energia per unità di tempo fornita
ad un elemento del circuito è:
P IΔV RI 2
ΔV 2
R
POTENZA
Tabella resistività elettrica di alcuni
materiali alla temperatura di
riferimento T=20 °C
Esercizio:
Una lampada ad incandescenza da 100W è alimentata a 220 V. Qual’è l’intensità di corrente che circola
nella lampada? E la resistenza?
P
100
P IΔV I
A 0.45A
ΔV
220
R
ΔV
220
Ω 484Ω
I
0.45
Esercizio:
Una lampada ad incandescenza da 50W è alimentata a 220 V. Qual’è la resistenza della lampada?
P
ΔV 2
R
R
ΔV 2
P
220 2
Ω 968 Ω
50
Esercizio:
Un filo di rame è attraversato da una corrente elettrica? Se si raddoppia la lunghezza del filo e si dimezza
la sezione, di quanto varia la resistenza?
R ρ
R1 ρ 1
A
A1
R2 ρ
2
2 1
4
ρ
ρ 1 4ρ 1 4R 1
1
A2
A1
A1
A1
2
R
R 2 4R 1
Esercizio:
Sapendo che la resistività del rame a 20 °C è ρ=0.017 Ω∙mm2/m, determinare la lunghezza che deve
avere un filo di rame di diametro 2mm affinhcè la resistnza alle temperatura di 20°C sia uguale ad 1Ω
R ρ
R π 4 d2
RA
1Ω 3.14 4 mm 2
184.7 m
A
ρ
ρ
4 0.017 Ωmm 2 m
Esercizio:
In un circuito passano in un’ora 4.5∙1022 elettroni. Quanto vale l’inensità di corrente?
ΔQ
4.5 10 22 1.6 10 19 C
I
2 C s 2A
Δt
3.6 10 3 s
Esercizio:
Il campo elettrico di un filo di rame percorso dalla corrente di 2A è 5∙10-3 V/m. Calcolare il diametro del
filo
ΔV E 5 10 3 V
La ddp su 1 m di filo è:
ΔV
5 10 3
R
Ω 2.5mΩ
I
2
Per la prima legge di Ohm:
Per la seconda legge di Ohm:
R ρ
A
1 m
0.017 Ωmm 2 m
6.8 mm 2
3
R
2.5 10 Ω
A ρ
d 2
A
2.9 mm
π
Esercizio:
Determinare la resistenza di un filo di rame a 100 °C, lungo 1000 m e di sezione 1mm2 sapendo che la
resistività a 20°C è 1.7∙102(Ωmm2/m) e che il coefficiente di temperatura a è 3.9∙10-3°C-1
La resistività di un elemento varia con la temperatura secondo la relazione:
ρ ρ o [1 α(T - To)]
Dove ρo è la resistività alla temperatura di riferimento To
La resistività del rame a 100°C sarà quindi:
ρ ρ o [1 α(T - To)] 1.7 10 -2 Ωmm 2 m 1 3.9·10 -3 C -1 100C 20C
ρ 2.2 10 - 2 Ωmm 2 m
R ρ
10 3 m
2.2 10 - 2 Ωmm 2 m
22Ω
A
1mm 2
CIRCUITI
Forza elettromotrice f.e.m.: Si definisce forza elettromotrice la tensione ai capi di un generatore
di tensione( batteria) quando la corrente è nulla ed è pari a ε. Se si considera la batteria come un
generatore ideale a resistenza nulla più una resistenza interna r, quando la batteria viene collegata
ad un circuito con una resistenza di carico R, la caduta di tensione ai capi della batteria è minore
della f.e.m ed è data da: ΔV= ε-rI=RI.
Si ha quindi che ε=(R+r)I
RESISTENZE IN SERIE
RESISTENZE IN PARALLELO
N
R eq
R
1
R eq
i
i 1
R1
Un circuito è costituito da:
1)un generatore di tensione (batteria)
2)un filo metallico
3)un interruttore
4)resistenze
5)rami (collegamento in serie di più elementi)
6)nodi (punto in cui corvergono almeno 3 rami)
7)maglie(insieme di due o più rami che formano
un cammino chiuso
+
N
R
1
i 1
i
Nodo 1
R2
R5
Maglia B
Nodo 3
Maglia A
R6
Nodo 2
R4
Maglia C
R7
Leggi di Kirchhoff:
1)La somma delle correnti che entrano in un nodo deve
essere uguale alla di quelle che ne escono.
Nodo 4
I
0
NODI
•I positiva se entra nel nodo
•I negativa se esce dal nodo
2) La somma delle ddp ai capi degli elementiappartenenti
ad una maglia deve essere nulla
ΔV
maglie
Dove:
•ΔV=-RI se la resistenza viene percorsa nel senso della corrente
•ΔV=+RI se il resistere viene percorso in senso opposto
•Se il generatore di tensione viene attraversato nel verso della f.e.m ( da
negativo a positivo) la variazione di porenziale è +ε
•Se il generatore di tensione viene attraversato nel verso opposto alla
f.e.m ( da positivo a negativo) la variazione di porenziale è -ε
0
R3
Per applicare i principi di Kirchhoff si deve:
1)Definire i rami del circuito ed applicare un verso arbitrario alla corrente per ogni ramo
2)Identificare la polarità della batteria
3) Determinare se parte del circuito può essere ridotto utilizzando resistenze equivalenti
4)Determinate le maglie ed i nodi del circuito
5)Disegnare il cicuito identificando tutte le resistenze e le correnti circolati su di esse
e le ddp ai loro capi
6)Applicare le prima legge di kirchhoff ai nodi (tranne uno) del circuito, quindi apllicare la seconda
Legge di kirchhoff ad un numero sufficiente di maglie da determinare tutte le incognite (in modo di
avere in totale un numero di equazioni nodi+ maglie= numero di incognite)
Esercizio:
Consideriamo la rete in figura:
Ricavare le correnti che scorrono nei vari rami del circuito
R5
ε1= 60V
ε2= 80V
ε4= 100V
R1=R2=R5=2kΩ
R3=20kΩ
R4=5kΩ
R1
R2
R4
R3
ε4
ε1
ε2
1) Definiamo i rami del circuito e assegnamo arbitrariamente un direzione di corrente per ogni ramo
I1
R
I
5
Nel circuito ci sono 6 rami per ognuno dei
quali viene assegnata una corrente
R1
R3
I3
I5
2
I4
R4
R2
ε4
ε1
ε2
I6
2) Definiamo la polarità (segno + -) ai capi dei resistori e dei generatori del circuito e definiamo
tutti i nodi (A, B, C, D) e le maglie (M1, M2, M3)
I1
R5
I2
A
B
N. Di rami: 6
N. Di nodi: 4
N. Di maglie 3
N correnti incognite: 6
R1
M1
ε1
R3
+
D
I3
I5
R4
M2
+
-
I6
I4
ε4
C
R2
+
M3 -
ε2
I1
R5
I2
A
Maglia M1
R1
Partiamo dal nodo D, arriviamo ad A
percorrendo il ramo 1 e torniamo a D
percorrendo il ramo 3
M1
R3
B
I3
+
-
ε1
D
I5
R4
M2
+
-
I6
I4
ε4
R2
+
M3 -
C
ε2
E 1 R 1 I1 R 3 I 3 0
Maglia M2
Partiamo dal nodo D, arriviamo ad A
percorrendo il ramo 3 andiamo a B,
percorrendo il ramo 5andiamo a C
percorrendo il ramo 4 e torniamo a D
percorrendo il ramo 6
Otteniamo:
R 3 I 3 R 5 I 5 R 4 I 4 E 4 0
Maglia M3
E4 R 4I4 R 2I2 E2 0
Partiamo dal nodo C, arriviamo a B
percorrendo il ramo 4 torniamo a C
percorrendo il ramo 2
Otteniamo:
I1
A
I5
I3
NODI:
I1 I 5 I 3 0
I 2 I 6 I 4 0
I 2 I 5 I 4 0
I1 I 5 I 3 0
E 4 R 4 I 4 R 2 I 2 E 2 0
R 3 I 3 R 5 I 5 R 4 I 4 E 4 0
E 1 R 1 I1 R 3 I 3 0
I5
I2
B
I4
I2 I5 I4 0
I4
I6
C
I2
I 2 I 6 I 4 0
100V 5kΩI 4 2kΩI 2 80 0
20kΩI 3 2kΩI 5 5kΩI 4 100V 0
60V 2kΩI1 20kΩI 3 0
I 2 I 6 I 4 0
I 2 I 5 I 4 0
I1 I 5 I 3 0
Bisogna a questo punto solo risolvere le equazioni
MOTO DI PARTICELLE CARICHE IN UN CAMPO PUNTIFORME
Esercizio:
Con riferimento alla figura precedente, determinare la velocità di arrivo dell’elettrone sullo schermo,
sapendo che il campo elettrico uniforme è presente solo nel tratto d .
Il lavoro fatto dal campo elettrico (se positivo, altrimenti fatto dalla carica per opporsi al campo)
è dato da F∙S=F∙d dove
F qE
Il teorema dell’energia cinetica afferma che il lavoro è
anche uguale alla variazione di energia cinetica,
cosicchè:
L Tf Ti
Da cui si trova:
1
m e v f2 v i2 qEd
2
vf
2qEd
v i2
m
Poichè il campo agisce solo nel tratto d l’elettrone,
superato tale tratto continuerà a viaggiare con velocità vf
Esercizio:
Moto in un campo elettrico trasverso
Determinare il punto di arrivo sullo schermo dell’elettrone mostrato nella figura seguente e calcolare
la velocità con cui vi arriva
Il campo è perpendicolare alla velocità iniziale dell’elettrone
Una volta che l’elettrone entra nel campo elettrico subisce una
forza lungo la direzione y data da F=qeE
Le equazioni del moto fino all’istante in cui l’elettrone esce
dal campo sono quindi:
ax 0
ay
t
Eq
F
me
me
x
v0
v x v xo v o
x x 0 v0t v0t
v y v yo a y t a y t y 0
y
1 Eq x 2
2 m e v 02
1
1 Eq 2
a yt2
t
2
2 me
Equazione di una parabola, che vale fin quando x<d
Quando l’elettrone ha raggiunto la distanza d si è spostato lungo l’asse y di un’altezza
1 Eq d 2
h
2 m e v 02
v x f v o
Eqd
d
Da quell’istante in poi si muoverà di moto rettilineo uniforme con velocità iniziale:
v yf a y v m v
o
e o
Il tempo impiegato dall’elettrone per raggiungere lo schermo (per percorrere la distanza l) è quindi: t
vo
E l’altezza hf del punto in cui l’elettrone raggiunge lo schermo è data da.
y h v yf t
hf
Eq d
1 Eq d 2
2 m e v 02
me v0 v0
qEdd 2
m e v 02












