Sintesi - Capitolo 2
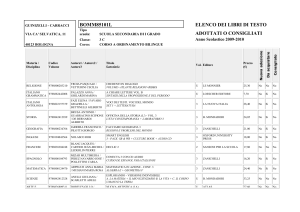
L'energia libera e gli equilibri chimici
Equazione di van't Hoff
Ricordando che G G8 RT ln P, se definiamo la variazione di energia libera di una reazione chimica
con la formula DG8 SG8prodotti SG8reagenti , per una generica reazione a A b B ! c C d D si ha
DG DG8 RT ln
pcC pdD
paA pbB
(equazione di van't Hoff )
Quando la reazione raggiunge l'equilibrio, DG 0 e il rapporto sotto il segno di logaritmo, che rimane
costante, viene chiamato costante di equilibrio (Kp):
DG8
RT ln Kp
L'equazione di van't Hoff puoÁ dunque essere riscritta nella forma
DG
RT ln Kp RT ln
pcC pdD
paA pbB
Come al solito, per reazioni in soluzione, al posto della pressione si usa la concentrazione (ricordando
sempre che, se il sistema non eÁ ideale, si devono introdurre le attivitaÁ).
Influenza della pressione
Da quanto detto potrebbe sembrare che l'andamento di una reazione dipenda soltanto dalla temperatura;
in realtaÁ, anche la pressione, ma solo per i componenti allo stato gassoso (dato che liquidi e solidi sono
quasi insensibili alle variazioni di pressione), esercita un'influenza importante su di esso.
Infatti, se consideriamo l'equazione di van't Hoff ed esprimiamo le pressioni mediante la legge di Dalton
(pA xA PA ), abbiamo
d
xc P c xdD Ptot
DG RT ln Kp RT ln Ca tot
a xb P b
xA Ptot
B tot
RT ln Kp RT ln
xcC xdD
cd
Ptot
xaA xbB
RT ln Kp RT ln
xcC xdD Dn
P
xaA xbB tot
a b
Dn
da cui si nota che il valore di DG viene a dipendere da Ptot
(dove Dn si riferisce solo ai composti gassosi).
Isobara di van't Hoff
La dipendenza dalla temperatura puoÁ invece essere ricavata da
da cui
ln Kp
DG8 DH8
DH8 DS8
RT
R
e
d ln Kp
d
dT
dT
TDS8
DH8 DS8
RT
R
RT ln Kp
DH8 DH
RT 2
RT
(isobara di van't Hoff )
poiche DS8=R eÁ costante e, per variazioni di temperatura non troppo elevate, DH8 DH.
Copyright ã 2010 Zanichelli Editore SpA, Bologna [6702]
Á una estensione online del corso Sergio Pasquetto, Luigi Patrone
Questo file e
Chimica Fisica settima edizione ã Zanichelli 2010
1
Sintesi ± Capitolo 2 . L'energia libera e gli equilibri chimici
La dipendenza di Kp dalla temperatura eÁ legata al segno di DH: per la reazione esotermica (DH < 0), la
dipendenza eÁ inversa; per la endotermica (DH > 0), invece, diretta.
L'isobara di van't Hoff puoÁ essere risolta per integrazione:
Z T2
Z T2
DH dT
d ln Kp
R T2
T1
T1
che, se DH eÁ costante nell'intervallo di temperatura considerato, daÁ
KP;T2 H 1
1
ln
R T1 T2
KP;T1
ln Kp
ΔH <
α
ΔH
>
Δy
0
0
Δx
1/T
Figura 2.2 Variazione di ln Kp in funzione di 1=T per reazioni esotermiche ed endotermiche.
Diagramma di Francis e diagramma di Ellingham
Spesso, peroÁ, al fine di visualizzare immediatamente la dipendenza di Kp da T, si rivela piuÁ utile una
rappresentazione grafica del tipo in figura, dove la pendenza delle rette eÁ DH=R.
G°/n (kJ/mol C)
100
80
60
CH
2
C 2H 4
2
40
C 6H 6
4
CH
6
H
2
C
8
3
C
H
20
C(grafite) ; H2
0
500
700
900 1100 1300 1500 1700 1900
Figura 2.3 Diagramma di Francis.
Copyright ã 2010 Zanichelli Editore SpA, Bologna [6702]
Á una estensione online del corso Sergio Pasquetto, Luigi Patrone
Questo file e
Chimica Fisica settima edizione ã Zanichelli 2010
2
T (K)
Sintesi ± Capitolo 2 . L'energia libera e gli equilibri chimici
Esempi pratici di rappresentazioni di questo tipo sono il diagramma di Francis e il diagramma di Ellingham,
utilizzati rispettivamente in petrolchimica e in metallurgia.
A livello molecolare, la costante di equilibrio puoÁ essere considerata come risultante dal compromesso
tra la tendenza a occupare i livelli a piuÁ bassa energia e quella a occupare il maggior numero di livelli per
raggiungere la distribuzione statisticamente piuÁ probabile.
ΔG° (kJ/mol)
200
O
2 Ag 2
0
2 CuO
2 PbO
–200
O2
+
2 CO
→2C
O 2←
CO2
2 CO
–600
l
2/3 A 2
O3
–1000
0
500
1000
1500
Figura 2.5 Diagramma di Ellingham.
Copyright ã 2010 Zanichelli Editore SpA, Bologna [6702]
Á una estensione online del corso Sergio Pasquetto, Luigi Patrone
Questo file e
Chimica Fisica settima edizione ã Zanichelli 2010
3
2000
2500 T (°C)