6.
FENOMENI DI TRASPORTO DI QUANTITA’ DI MOTO E DI ENERGIA
6.1
Equazioni di conservazione della quantità di moto e dell’energia
Nel Capitolo 5 abbiamo visto che la forma più generale delle equazioni di conservazione o di
bilancio può essere scritta nel seguente modo:
Variazione nell’unità
di tempo del contenuto
di entità all’interno del
volume di controllo V
=
Entità generata o
consumata nell’unità di
tempo all’interno del
volume di controllo V
Portata netta di entità
entrante nel volume di
controllo V attraverso la
superficie S
(6.1)
dove per entità intendiamo una qualunque grandezza fisica f per la quale valga il principio di
conservazione. Scritta in forma più concisa, la (6.1) diviene:
Af R f Eˆ f
(6.2)
Nei capitoli precedenti abbiamo focalizzato l’attenzione sui fenomeni di trasporto di materia e
quindi abbiamo identificato f con la quantità di materia. In questo capitolo prenderemo in
considerazione i fenomeni di trasporto di altre due grandezze fisiche, la quantità di moto e l’energia,
e conseguentemente scriveremo le equazioni di bilancio identificando f con esse. Con riferimento a
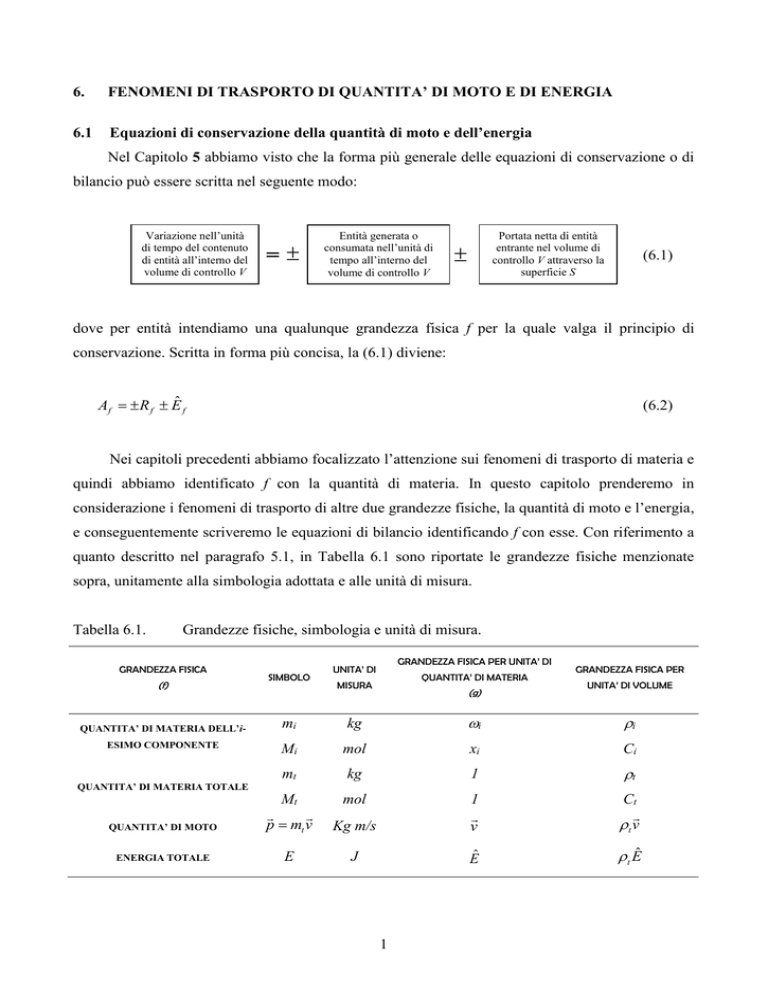
quanto descritto nel paragrafo 5.1, in Tabella 6.1 sono riportate le grandezze fisiche menzionate
sopra, unitamente alla simbologia adottata e alle unità di misura.
Tabella 6.1.
Grandezze fisiche, simbologia e unità di misura.
GRANDEZZA FISICA
(f)
SIMBOLO
GRANDEZZA FISICA PER UNITA’ DI
UNITA’ DI
QUANTITA’ DI MATERIA
MISURA
(g)
GRANDEZZA FISICA PER
UNITA’ DI VOLUME
QUANTITA’ DI MATERIA DELL’i-
mi
kg
i
i
ESIMO COMPONENTE
Mi
mol
xi
Ci
mt
kg
1
t
mol
QUANTITA’ DI MOTO
Mt
p mt v
Kg m/s
1
v
Ct
t v
ENERGIA TOTALE
E
J
Ê
t Eˆ
QUANTITA’ DI MATERIA TOTALE
1
Tenendo presente quanto riportato nel paragrafo 5.1, il bilancio macroscopico per una
generica grandezza f può essere scritto come segue:
df
f dV f n ds
dt
V
S
(6.3)
la quale identificando f con la quantità di moto diventa:
dp
p dV p n ds
dt
V
S
(6.4)
mentre il bilancio macroscopico di energia totale è dato dalle seguente equazione:
dE
E dV E n ds
dt
V
S
(6.5)
nella quale la grandezza fisica f è stata assimilata all’energia totale del sistema E.
Nel prossimo paragrafo verranno illustrati i diversi fenomeni di trasporto che contribuiscono
al flusso totale di quantità di moto p e di energia totale E , i quali appaiono rispettivamente nelle
equazioni (6.4) e (6.5), mentre successivamente vedremo quali sono i fenomeni fisici che
concorrono a determinare i termini di generazione o scomparsa p e E .
6.2
Fenomeni di trasporto di quantità di moto e di energia
Abbiamo visto nei capitoli precedenti che i fenomeni di trasporto di materia possono essere di
due tipi: uno associato al moto d’insieme delle molecole o degli atomi che compongono il sistema
in esame, detto trasporto di tipo convettivo, e un altro dipendente dal moto dei singoli atomi o
molecole e dalle interazioni che avvengono tra loro, il quale prende il nome di diffusione o trasporto
diffusivo, ma che in generale viene detto trasporto di tipo molecolare. Un discorso analogo può
essere fatto in generale per il trasporto di una qualunque grandezza fisica, e in particolare, per il
trasporto di quantità di moto o di energia.
Per quanto riguarda il trasporto di tipo convettivo, il flusso ad esso associato è esprimibile
mediante la seguente relazione:
2
flusso
convettivo t
grandezza fisica f
per unità di quantità di materia (in unità massiche) v
(6.6a)
flusso
grandezza fisica f
convettivo Ct per unità di quantità di materia (in unità molari ) v
(6.6b)
In Tabella 6.2 sono riportate le espressioni e le unità di misura del flusso convettivo delle diverse
grandezze fisiche incontrate.
Tabella 6.2.
Grandezze fisiche, flusso convettivo, simbologia e unità di misura.
GRANDEZZA FISICA
(f)
GRANDEZZA FISICA PER UNITA’
DI QUANTITA’ DI MATERIA
QUANTITA’ DI MATERIA DELL’i-
(g)
i
FLUSSO
UNITA’ DI
CONVETTIVO
MISURA
iv
QUANTITA’ DI MOTO
1
v
Ci v
t v
Ct v
t v v
ENERGIA TOTALE
Ê
t Eˆ v
ESIMO COMPONENTE
QUANTITA’ DI MATERIA
TOTALE
xi
1
kg / m2 s
mol / m2 s
kg / m2 s
mol / m2 s
kg / m s2
J / m2 s
Al fine ora di descrivere il trasporto molecolare di quantità di moto si consideri, con
riferimento alla Figura 6.1, un fluido contenuto tra due superfici parallele molto estese di area A,
separate da una distanza Y molto piccola. Supponiamo che il sistema sia inizialmente in quiete, ma
che al tempo t=0 la piastra inferiore venga messa in movimento nella direzione x con una velocità
costante V. Con il tempo, il fluido acquista una certa quantità di moto fino a che, in condizioni di
regime stazionario, si stabilisce un profilo spaziale (lungo y) di velocità come quello mostrato in
figura. Durante tutto il processo sopra descritto, per mantenere in moto la piastra inferiore è
necessaria una forza per unità di superficie (sforzo) pari alla tensione tangenziale esercitata sulla
superficie della piastra inferiore dal fluido che si trova a contatto con essa, per effetto della
differenza di velocità che si ha tra i diversi strati del fluido in movimento. In particolare, per il caso
riportato in Figura 6.1 possiamo scrivere:
3
yx
dvx
dy
(6.7)
la quale dice che la tensione tangenziale esercitata dal fluido sulla superficie della piastra lungo la
direzione x per effetto del gradiente di velocità lungo la direzione y e proporzionale al gradiente
stesso con il segno negativo, dove la costante di proporzionalità è la viscosità del fluido.
La (6.7) può essere considerata anche da un altro punto di vista. In prossimità di una
superficie in movimento, per y=0, il fluido acquista una certa quantità di moto nella direzione x;
questo fluido a sua volta conferisce una parte della sua quantità di moto agli strati adiacenti,
consentendo ad essi di mettersi in movimento nella direzione x, e trasmettendo in questo modo la
quantità di moto nella direzione y. Pertanto yx può anche riguardarsi come il flusso della
componente x della quantità di moto nella direzione y. Questa interpretazione del fenomeno è più
conforme alla natura molecolare del processo di trasporto della quantità di moto (detto anche flusso
viscoso) ed è analogo a quello già visto per la diffusione (trasporto di materia) e a quello che si
vedrà per la conduzione (trasporto di energia termica o calore).
Figura 6.1 Evoluzione del profilo di velocità per un fluido contenuto tra due piastre.
Dalla (6.7) si può anche vedere come il flusso di quantità di moto avviene nella direzione
contraria al gradiente di velocità (da qui il segno negativo), cioè, la quantità di moto ha la tendenza
a trasferirsi nella direzione lungo la quale diminuisce la velocità. In altre parole, la quantità di moto
viene trasportata da zone ad alta velocità verso zone a bassa velocità, così come la materia diffonde
da zone ad alta concentrazione verso zone a bassa concentrazione. Pertanto, un gradiente di velocità
4
può essere riguardato come una forza motrice per il trasporto molecolare di quantità di moto, così
come il gradiente di concentrazione lo era per il trasporto molecolare di materia.
Nel caso di un sistema in cui le componenti della velocità vx, vy, vz, siano tutte diverse da zero
e varino lungo le tre coordinate spaziali (x, y, z), la (6.7) assume la forma:
(v v (T ) )
(6.8)
in cui rappresenta il tensore degli sforzi, rappresentato dalla seguente matrice
xx yx zx
xy yy zy
xz yz zz
(6.9)
e dove il gradiente della velocità è anch’esso una matrice:
v x
x
v
v y
x
v z
x
v x
y
v y
y
v z
y
v x
z
v y
z
v z
z
(6.10)
così come lo è la sua trasposta (v (T ) ) .
La (6.8) esprime la legge di Newton e i fluidi che seguono questa legge vengono detti fluidi
newtoniani. Tutti i gas e la maggior parte dei liquidi semplici seguono questa legge, mentre le paste,
le sospensioni, i polimeri, nonché fluidi complessi come il sangue obbediscono a leggi diverse e
vengono denominati fluidi non newtoniani.
Consideriamo ora il trasporto molecolare di energia termica o più comunemente di calore. In
particolare, con riferimento alla Figura 6.2, si supponga di avere uno strato costituito da un solido o
da un fluido in quiete compreso tra due piastre parallele a distanza Y l’una dall’altra. Si supponga
che il sistema si trovi inizialmente tutto alla temperatura T0. Al tempo t=0 la piastra inferiore viene
portata immediatamente ad una temperatura T1 > T0 e mantenuta a detta temperatura. Al procedere
del tempo, il profilo di temperatura nello strato varia sino a raggiungere alla fine una distribuzione
stazionaria lineare. Durante il processo di riscaldamento e il mantenimento dello stato stazionario
5
sopra descritto, il flusso di calore che attraversa lo strato tra le due piastre può essere valutato
mediante la seguente relazione:
qc y k
dT
dy
(6.11)
la quale stabilisce che il flusso di calore lungo la direzione y e proporzionale al gradiente di
temperatura lungo y attraverso la conducibilità termica k. Quest’ultima dipende in generale dalla
natura fisica e chimica dello strato, dalla temperatura e dalla pressione.
In un sistema in cui la temperatura varia lungo le tre direzioni (x, y, z), la (6.11) assume la
forma:
qc kT
(6.12)
Figura 6.2 Sviluppo del profilo di temperatura per uno strato contenuto tra due piastre.
La (6.11) e la (6.12) più in generale sono forme della cosiddetta legge di Fourier per la
conduzione termica, la quale dice che il vettore flusso termico qc è proporzionale al gradiente di
temperatura ed è diretto in senso opposto, ovvero il calore si trasmette da zone ad alta temperatura a
zone a bassa temperatura.
A questo punto è facile osservare che c’è una stretta analogia tra il trasporto molecolare di
materia, quantità di moto e calore. In ognuno di questi casi, infatti, il flusso molecolare è
proporzionale al gradiente negativo di una grandezza macroscopica e i coefficienti di
6
proporzionalità sono proprietà fisiche dipendenti dalla composizione del sistema, dalla temperatura
e dalla pressione. In Tabella 6.3 è riportato un riepilogo dei diversi fenomeni di trasporto
molecolare che possono avvenire in un sistema non isotermo in movimento e costituito da più
componenti.
Tabella 6.3.
Flussi molecolari, simbologia e unità di misura.
VARIABILE
GRANDEZZA FISICA
FLUSSO
MACROSCOPICA IL CUI
(f)
MOLECOLARE
GRADIENTE SPAZIALE
DETERMINA IL FLUSSO
QUANTITA’ DI MATERIA
DELL’i-ESIMO COMPONENTE
ji
J i*
COSTANTE DI
PROPORZIONALITA’ E
UNITA’ DI MISURA
LEGGE
COSTITUITIVA
i
Di [m2/s]
Fick
Di [m2/s]
Fick
[Pa s]
Newton
k [W / m2 s]
Fourier
QUANTITA’ DI MOTO
xi
v
ENERGIA TOTALE
qc
T
E’ interessante osservare che il trasporto molecolare di materia (diffusione) è assente in
sistemi costituiti da un solo componente, il trasporto molecolare di quantità di moto (trasporto
viscoso) è nullo nei sistemi in quiete, mentre la conduzione del calore (trasporto molecolare di
energia termica) non avviene nei sistemi isotermi.
Una importante differenza consiste però nel fatto che mentre la concentrazione e la
temperatura sono grandezze scalari, la velocità è una grandezza vettoriale. Conseguentemente, il
flusso di materia e quello di calore sono dei vettori con tre componenti, mentre il flusso di quantità
di moto è un tensore con nove componenti (cfr. eq. (6.9)).
Prima di concludere questo paragrafo può essere utile almeno accennare a due ulteriori
fenomeni di trasporto del calore, l’irraggiamento e la diffusione. L'irraggiamento è una forma di
trasmissione dell'energia che, al contrario della conduzione e della convezione, non prevede
contatto diretto della materia, e non necessita di un mezzo per propagarsi. Nell'irraggiamento la
trasmissione di energia avviene attraverso l'emissione e l'assorbimento di radiazione
elettromagnetica. Un esempio di notevole importanza in cui si esplica questo fenomeno è il
trasferimento di energia tra il Sole e la Terra. Questo meccanismo di trasporto è descritto
quantitativamente dalla legge di Stefan-Boltzmann:
qr T 4
(6.13)
7
dove è l’emissività che dipende dalla natura della superficie che irradia, è la costante di StefanBoltzmann e T è la temperatura della superficie irradiante. Questo tipo di trasporto di calore è
importante quando la temperatura del sistema è molto elevata.
Per descrivere il trasporto di calore per diffusione si consideri la Figura 6.3 in cui un fase
liquida in quiete è messa a contatto con una parete di una sostanza A solubile in essa. Sia la
temperatura della parete T2 mentre la temperatura della parete di fronte (insolubile nella fase
liquida) sia T1 < T2. Per effetto della dissoluzione di A si instaurerà un flusso diffusivo dalla parete a
temperatura T2 verso quella a temperatura T1, e le molecole di A diffonderanno pertanto verso zone
in cui la temperatura è via via minore. Questo fatto fa sì che al moto diffusivo sia associato oltre al
trasporto di materia, anche un trasporto di calore dovuto alla differenza di temperatura che esiste tra
un punto e un altro all’interno del liquido. Il contributo al trasporto di calore dovuto alla diffusione
in un sistema costituito da n componenti può essere quantificato mediante la relazione generale:
n
qd Hˆ i ji
i 1
(6.14)
dove Ĥ i rappresenta l’entalpia specifica (per unità di massa) del i-esimo componente, la quale
esprime il contenuto di energia termica del componente.
T2
Parete
solubile
T1
qd
Fase liquida
Parete
insolubile
ji
Figura 6.3 Trasporto di calore per diffusione.
E’ importante osservare che questo tipo di trasporto di calore esiste solo se si instaurano
contemporaneamente gradienti di concentrazione e di temperatura. Infatti, con riferimento alla
Figura 6.3, se la parete a temperatura maggiore non fosse solubile nella fase liquida, si avrebbe nel
sistema solo un trasporto di calore per conduzione descritto dalla legge di Fourier. Analogamente,
8
se le due pareti che contengono il liquido avessero uguale temperatura, si avrebbe solo un trasporto
di materia per diffusione descritto dalla legge di Fick.
6.3
Forze e bilancio macroscopico di quantità di moto
L’equazione di bilancio (6.4) esprime la variazione nel tempo del contenuto di quantità di
moto all’ interno del volume di controllo V per effetto dei fenomeni di trasporto che determinano il
flusso netto entrante attraverso la superficie S che contorna V e dei fenomeni di generazione o
scomparsa. Nei capitoli precedenti si è visto come nel caso dei bilanci di materia, i fenomeni di
generazione o scomparsa possono essere identificati con le reazioni chimiche che avvengono
all’interno del sistema su cui si sta facendo il bilancio. Nel caso invece della quantità di moto, il
termine di generazione o scomparsa p è dato dalla risultante delle forze agenti sul sistema. In
particolare, le forze possono essere suddivise in due categorie: le forze di superficie agenti sulla
superficie S che contorna il volume di controllo V e le forze agenti su quest’ultimo e quindi forze di
volume. Tenendo conto delle considerazioni fatte, il bilancio macroscopico di quantità di moto può
essere espresso nella forma:
Variazione nell’unità
di tempo del
contenuto di quantità
di moto all’interno
del volume di
controllo V
=
Portata netta di
quantità di moto
entrante nel volume
di controllo V
attraverso la
superficie S
+
Risultante
delle forze di
volume
agenti sul
volume di
controllo V
+
Risultante delle
forze di superficie
agenti sulla
superficie S del
volume di controllo
V
(6.15)
Pertanto, esprimendo il flusso totale di quantità di moto come la somma del flusso convettivo e del
flusso viscoso, possiamo scrivere il bilancio macroscopico di quantità di moto come:
dp
( t vv ) nds FS FV
dt
S
(6.16)
Identificando le forse di superficie con le forze di pressione e le forze di volume con la forza
di gravità, possiamo scrivere che:
FS P n ds
(6.17)
S
e
9
FV t g dV
(6.18)
V
dove g rappresenta il vettore accelerazione di gravità. Inoltre, la quantità di moto può anche essere
espressa come:
p t v dV
(6.19)
V
Sostituendo la (6.17)-(6.19) nella (6.16), il bilancio macroscopico di quantità di moto assume la
forma:
d
t v dV ( t vv ) nds p n ds t g dV
dt V
S
S
V
(6.20)
il quale una volta risolto fornisce la variazione nel tempo della quantità di moto contenuta
all’interno del sistema, e la velocità media del fluido presente al suo interno.
6.4
Trasformazioni e bilancio macroscopico di energia totale
Nel paragrafo precedente abbiamo visto quali sono i diversi fenomeni di trasporto di energia
che si possono incontrare più frequentemente nello studio dei sistemi biologici o biomedici e che
quindi contribuiscono al flusso netto di energia totale entrante in un determinato sistema. Un
discorso particolare merita invece il termine di generazione o scomparsa E che appare
nell’equazione di bilancio (6.5). Infatti, in assenza di reazioni nucleari, le quali trasformano la
materia in energia, il principio di conservazione dell’energia totale dice che l’energia totale non può
essere né generata ne consumata, e pertanto risulta improprio il significato attribuito sino ad ora a
E. In realtà esso rappresenta l’energia scambiata dal sistema con l’ambiente circostante attraverso
trasformazioni dell’energia nella sue diverse forme, ovvero il lavoro compiuto per unità di tempo
dal sistema sull’ambiente circostante o il lavoro compiuto per unità di tempo da quest’ultimo sul
sistema.
Pertanto, il bilancio macroscopico di energia totale può essere riscritto più propriamente nella
forma:
Variazione nell’unità di
tempo del contenuto di
energia totale all’interno
del volume di controllo V
=
Portata netta di energia
totale entrante nel
volume di controllo V
attraverso la superficie S
10
Lavoro compiuto dal sistema
sull’ambiente circostante o da
quest’ultimo sul sistema
nell’unità di tempo
(6.21)
Tenendo conto di quanto esposto nel paragrafo 6.2 possiamo esprimere come segue il bilancio
macroscopico di energia totale:
E
t Eˆ v qc qr qd n ds L ( S )P L ( s )v L (V ) L ( e)
t
S
(6.22)
Il termine di accumulo che appare nell’equazione di bilancio (6.22) rappresenta la variazione
nell’unità di tempo dell’energia totale contenuta all’interno del volume di controllo V. Il primo
termine del secondo membro rappresenta la portata netta di energia totale entrante all’interno del
volume di controllo attraverso la superficie S che lo contorna. In particolare, il flusso totale è dato
dalla somma dei contributi dovuti ai diversi fenomeni di trasporto di energia che in generale
possono essere presenti: convezione ( t Eˆ v ), conduzione ( qc ), irraggiamento ( qr ) e diffusione
( q d ). Gli ultimi quattro termini rappresentano invece l’energia totale acquistata o persa dal sistema
per unità di tempo (lavoro) per effetto delle trasformazioni di energia dovute alle interazioni tra il
sistema e l’ambiente circostante. In particolare:
L ( S ) P è il lavoro compiuto nell’unità di tempo dalle forze di pressione agenti sulla superficie
S del volume di controllo V, positivo se compiuto dall’ambiente esterno sul sistema,
negativo se erogato dal sistema sull’ambiente circostante.
L ( S )v è il lavoro compiuto nell’unità di tempo dalle forze viscose agenti sulla superficie S
del volume di controllo V, positivo se compiuto dall’ambiente esterno sul sistema, negativo
se prodotto dal sistema e fornito all’ambiente circostante.
L (V ) è il lavoro compiuto nell’unità di tempo dalle forze di volume (gravità) agenti sul
volume di controllo V, positivo se compiuto dall’ambiente esterno sul sistema, negativo se
fornito dal sistema all’ambiente circostante.
L (e ) è il lavoro compiuto nell’unità di tempo dal sistema su macchinari o loro parti inserite
nel sistema ed erogato all’esterno (contributo negativo) o compiuto da macchinari o loro
parti inserite nel sistema e fornito a quest’ultimo (contributo positivo).
La (6.22) una volta risolta fornisce la variazione nel tempo del contenuto di energia totale
del sistema dovuta ai diversi fenomeni di trasporto e di trasformazione che avvengono al suo
11
interno o sulla sua superficie. Tuttavia, la (6.22) risulta generalmente di scarso interesse applicativo
in quanto sono rari i casi in cui si è interessati all’energia totale piuttosto che a sue forme
particolari. Infatti, trascurando forme di energia quali quella nucleare o elettromagnetica possiamo
esprimere l’energia totale come:
E U K
(6.23)
ovvero come la somma dell’energia interna U, la quale rappresenta l'energia immagazzinata dalle
molecole e/o atomi costituenti il sistema, dell’energia cinetica K, determinata dalla velocità con cui
si muove il sistema nel suo complesso e dell’energia potenziale , la quale è una funzione della
posizione del sistema all’interno del campo gravitazionale.
Tipicamente, la somma dell’energia cinetica e dell’energia potenziale viene detta energia
meccanica mentre l’energia interna viene anche identificata come energia termica. Di seguito
focalizzeremo l’attenzione sull’energia termica mentre le tematiche inerenti l’energia meccanica
verranno approfondite in altri corsi.
Identificando l’energia termica mediante la variabile U è possibile scrivere il seguente
bilancio di energia termica:
U
tUˆ v qc qr qd n ds L((US ))P L ( s )v
t
S
(6.24)
Il membro a sinistra della (6.24) esprime la variazione nell’unità di tempo del contenuto di
energia termica del sistema, mentre il primo termine del secondo membro rappresenta la portata
netta di energia termica entrante nel sistema. In particolare, si noti come il termine convettivo tiene
conto in questo caso unicamente dell’energia termica U, contrariamente alla (6.22) in cui il termine
corrispondente rappresentava la portata netta di energia totale E entrante per convezione. I flussi di
energia conduttivo, radiante e diffusivo sono presenti inalterati nella (6.24) in quanto espressione di
fenomeni di trasporto che coinvolgono solo l’energia termica.
Per quanto riguarda i termini di trasformazione dell’energia, confrontando la (6.22) con la
(6.24), si nota come in quest’ultima non sono presenti i termini L (V ) e L (e ) in quanto essi
determinano una variazione del contenuto di energia meccanica di un sistema senza però alterare il
contenuto di energia termica. Il lavoro compiuto dalla forze viscose, L ( s )v , rappresenta sempre una
trasformazione di energia meccanica in energia termica e pertanto appare ancora nella (6.24). Le
12
forze di pressione, invece, possono in generale dar luogo a variazioni sia del contenuto di energia
termica sia a variazioni del contenuto di energia meccanica, ed è pertanto esprimibile come somma
di due contributi:
L ( S )P L((US ))P L((KS)P )
(6.25)
Di conseguenza, nell’equazione di bilancio (6.24) appare solo la parte del lavoro compiuto dalle
forze di pressione che determina una variazione del contenuto di energia termica del sistema.
La (6.24) risulta ancora di difficile applicazione pratica in quanto non dipendente
esplicitamente dalla variabile che più comunemente viene utilizzata per esprimere il contenuto di
energia termica di un sistema, ovvero la temperatura. Per arrivare ad un bilancio di energia termica
espresso in funzione della temperatura è necessario prima introdurre una nuova funzione
termodinamica, l’entalpia H, e la corrispondente entalpia specifica (entalpia per unità di massa) Ĥ .
L’entalpia è legata all’energia interna dalla seguente relazione termodinamica:
U H PV
(6.26)
mentre il legame tra le corrispondenti grandezze specifiche è dato da:
P
Uˆ Hˆ
(6.27)
t
Sostituendo la (6.26) e (6.27) nella (6.24) otteniamo la seguente espressione del bilancio di
energia termica:
H
(H )
ˆ
t H v qc qr qd n ds L( S )P L ( s )v
t
S
(6.28)
detto anche bilancio entalpico. Si noti come in questo bilancio anche il termine che tiene conto del
lavoro compiuto dalla forze di pressione è espresso in funzione della grandezza termodinamica H.
Riguardo quest’ultima grandezza fisica, la termodinamica ci dice che è in generale una
funzione della temperatura, della pressione e della composizione del sistema. Pertanto con passaggi
matematici che in questa sede omettiamo, è possibile ottenere il seguente bilancio di energia
termica:
13
mt C p
m
T
t C pT v qc qr qd n ds L((TS ,)PP ) L( s )v V H R j rj'
t
S
j 1
(6.29)
la quale esprime la variazione nel tempo della temperatura del sistema. Nella (6.29) è stata
introdotta la proprietà termofisica Cp, detta calore specifico a pressione costante. Si noti come il
flusso convettivo sia espresso anch’esso in funzione della temperatura e come il lavoro compiuto
dalle forze di pressione dipenda dalla temperatura e dalla pressione stessa del sistema. Inoltre, nella
(6.29) compare ora un nuovo termine di generazione o scomparsa di energia termica, il quale
esprime il calore generato o sottratto delle m reazioni che avvengono all’interno del volume di
controllo V, e in cui H R j rappresenta la variazione di entalpia associata alla j-esima reazione
chimica che avviene nel sistema, positivo se la reazione è endotermica (assorbe calore), negativo se
è esotermica (libera calore).
6.5
Bilanci microscopici di quantità di moto e energia termica
Si consideri un sistema non isotermo costituito da una fase fluida in movimento e in cui sono
presenti n specie chimiche e in cui avvengono m reazioni chimiche. Per avere una completa
descrizione del sistema che stiamo studiando è necessario conoscere come varia nel tempo e nello
spazio la composizione, la velocità e la temperatura. A tale scopo i bilanci macroscopici ricavati nel
paragrafo precedente non rappresentano lo strumento matematico più adatto, e pertanto è necessario
utilizzare i bilanci microscopici o locali. Di seguito descriveremo i bilanci microscopici di quantità
di moto e di energia termica, tralasciando i passaggi matematici necessari per ricavarli partendo dai
bilanci globali, per altro simili a quelli descritti nel Capitolo 5.
Al fine di semplificare la trattazione, supponiamo che la fase fluida che vogliamo descrivere
sia diluita e incomprimibile, da cui la ragionevole assunzione che la concentrazione massica totale e
la concentrazione molare totale non varino nel tempo e nello spazio. Sotto queste assunzioni
semplificative, i profili spaziali e temporali della concentrazione dei singoli componenti possono
essere determinati per mezzo del seguente bilancio di materia:
m
Ci
v Ci Di 2Ci vi , j rj 0
t
j 1
(6.30)
o in alternativa
14
m
i
v i Di 2 i vi , j rj' 0
t
j 1
(6.31)
dove, in entrambi i bilanci (6.30) e (6.31) si è ipotizzato che la diffusività della generica specie
chimica i sia indipendente dalla composizione e dalla temperatura.
La velocità del fluido v che appare nelle (6.30) e (6.31) è anch’essa una funzione del tempo e
dello spazio, ed è pertanto necessario risolvere unitamente ai bilanci di materia per gli n componenti
presenti nel sistema, anche il bilancio microscopico di quantità di moto. Aggiungendo alle ipotesi
semplificative adottate sopra, che la viscosità del fluido che supporremo newtoniano non vari al
variare della composizione e della temperatura, il bilancio di quantità di moto microscopico assume
la forma:
t
v
t v v 2 v P t g 0
t
(6.32)
dove il penultimo e ultimo termine rappresentano rispettivamente la risultante delle forze di
pressione e della forza di gravità che agiscono sul fluido e ne determinano una variazione del
contenuto di quantità di moto. Il bilancio di quantità di moto scritto nella forma della (6.32) è detta
equazione di Navier-Stokes, la quale rappresenta una delle equazioni fondamentali per la
risoluzione della fluidodinamica di un sistema. Dividendo la (6.32) per la concentrazione massica
totale si ottiene:
P
v
v v 2v g 0
t
t
(6.33)
dove è stata introdotta la proprietà nota come viscosità cinematica , definita come il rapporto tra la
viscosità e la densità.
Avendo supposto il sistema in studio non isotermo, la sua temperatura varierà nel tempo e
nello spazio. È pertanto necessario unire ai bilanci di materia e al bilancio di quantità di moto anche
il bilancio di energia termica, il quale una volta risolto consente di ottenere i profili temporali e
spaziali della temperatura del sistema. Considerando indipendenti dalla temperatura e dalla
composizione le sue proprietà termofisiche (calore specifico a pressione costante Cp e conducibilità
termica k) il bilancio microscopico di energia termica può essere scritto nel seguente modo:
15
t C p
m
T
t C p v T k 2T H R j rj 0
t
j 1
(6.34)
Si noti che nel bilancio di energia appena scritto sono stati trascurati i contributi dovuti al
flusso di calore per irraggiamento qr , alla diffusione q d e ai termini di trasformazione dell’energia
derivanti dalla forze di superficie, L((Ts ),PP ) e , L ( s )v . Dividendo ora entrambi i membri della (6.34) per
il prodotto t C p , otteniamo il bilancio di energia nella forma:
m H
T
Rj
v T 2T
rj 0
t
j 1 t C p
(6.35)
in cui è stata introdotta la diffusività termica data dalla relazione:
k
t C p
(6.36)
Le n + 2 equazioni di bilancio (una per ogni componete del sistema più una per la quantità di
moto più una per l’energia termica) costituiscono quello che in termini matematici è detto sistema
di equazioni differenziali alle derivate parziali, il quale risolto fornisce la variazione nel tempo e
nello spazio della composizione, della velocità e della temperatura all’interno del sistema descritto
dalla equazioni di bilancio.
In Tabella 6.4 sono raggruppati i vari termini delle equazioni di bilancio in modo da rendere
più facile la comprensione del loro significato e le analogie. Si può notare come il termine di
variazione della grandezza fisica di cui si fa il bilancio è espresso mediante la derivata parziale
rispetto al tempo della variabile che descrive il sistema (i, Ci, v , T). Il secondo termine del
bilancio che deriva dal flusso convettivo della grandezza fisica è invece dato dal prodotto scalare tra
il vettore velocità e il gradiente spaziale della variabile descrittiva. Infine, i flussi di tipo molecolare
vengono descritti nel bilancio attraverso il prodotto di una “diffusività” per il laplaciano della
variabile descrittiva. E’ importante notare che il contributo di tipo molecolare che appare nel
bilancio di materia è stato ottenuto descrivendo il flusso diffusivo mediante la legge di Fick, mentre
le espressioni dei contributi dovuti al trasporto molecolare di quantità di moto e energia termica che
appaiono nei rispettivi bilanci sono stati ricavati utilizzando rispettivamente la legge di Newton e la
16
legge di Fourier. Si noti come la diffusività Di, la viscosità cinematica e la diffusività termica
hanno le stesse unità di misura.
Tabella 6.4. Rappresentazione schematica dei vari contributi ai bilanci microscopici
GRANDEZZA
FISICA
Quantità di
materia della
generica
specie chimica
i
mi o Mi
Quantità di
moto
mt v
VARIABILE
DESCRITTIVA
DEL SISTEMA
Variazione
nell’unità di
tempo del
contenuto della
grandezza fisica
per unità di
volume
Variazione
nell’unità di
tempo del
contenuto della
grandezza fisica
per unità di
volume per
effetto del flusso
convettivo
i
i
t
v i
Ci
C i
t
v Ci
v
v
t
v v
Variazione
nell’unità di
tempo del
contenuto della
grandezza fisica
per unità di
volume per effetto
del flusso
molecolare
Variazione nell’unità di tempo del contenuto
della grandezza fisica per unità di volume
per effetto dei fenomeni di generazione,
scomparsa, trasformazione o per effetto delle
forze applicate
Di 2 i
Massa della
generica specie
chimica i generata o
consumata da
reazioni chimiche
vi , j rj'
Di Ci
Moli della generica
specie chimica i
generata o
consumata da
reazioni chimiche
vi , j rj
Forze di pressione
P
t
2
2 v
Forza di gravità
Energia
termica
T
mt C pT
6.6
T
t
v T
T
2
Energia termica
(calore) sviluppata o
sottratta da reazioni
chimiche
m
j 1
m
j 1
g
m H
Rj
rj
j 1 t C p
Trasferimento di quantità di moto e di energia tra le fasi
Si consideri una fase messa a contatto con una fase , entrambe costituite da n componenti
e separate per mezzo di una superficie di separazione o interfaccia I. Con riferimento alla Figura
6.4, è in generale possibile che attraverso I avvenga un trasferimento di materia, così come di
quantità di moto o energia. Abbiamo visto nel Capitolo 4 come il trasferimento di materia tra le
diverse fasi avvenga sotto opportune condizioni semplificative (basse velocità di trasferimento di
materia) solo per diffusione. Pertanto, la quantità di materia della generica specie chimica i che
attraversa l’interfaccia di separazione tra le fasi per unità di superficie e per unità di tempo può
17
essere rappresentata dal flusso diffusivo ji , se utilizziamo le unità massiche, o J i* , se le unità
molari sono adoperate come misura della quantità di materia.
In analogia a quanto fatto per il trasporto di materia possiamo ora estendere il discorso al
trasporto di quantità di moto e al trasporto di energia. In particolare, supporremo che in entrambi i
casi i fenomeni di trasporto che contribuiscono al trasferimento di quantità di moto e di energia
attraverso l’interfaccia I, siano unicamente quelli di tipo molecolare. Pertanto, il trasferimento di
quantità di moto attraverso I sarà dato dal flusso molecolare di quantità di moto . Per quanto
riguarda il trasferimento di energia, limitiamo la nostra analisi alla sola energia termica, per cui il
flusso di energia termica q che attraversa l’interfaccia di separazione I sarà dato dalla somma del
flusso conduttivo qc , del flusso radiante qr e del flusso dovuto alla diffusione di materia q d .
Fase
Fase
*
ji , J i
q
I
Figura 6.4 Trasporto di materia, quantità di moto e energia termica tra le fasi.
Durante il corso abbiamo visto come durante il trasferimento di materia tra fasi diverse, in
corrispondenza della superficie di separazione tra esse, si instaura la condizione di uguaglianza
della componente dei flussi lungo la normale a I:
J i*( ) n J i*( ) n
I
(6.37)
I
o analogamente
( ) ( )
ji
n ji
n
I
(6.38)
I
Le condizioni (6.37) e (6.38) esprimono il fatto che all’interfaccia di separazione tra fasi diverse
non ci può essere un accumulo di materia, in quanto il volume di I è nullo.
18
Il concetto sopra esposto può essere estrapolato al trasferimento di quantità di moto e di
energia termica. Infatti, sulla superficie di separazione tra le fasi valgono le seguenti condizioni:
( ) I n ( ) I n
(6.39)
q ( ) n q ( ) n
(6.40)
e
I
I
le quali esprimono la condizione per cui all’interfaccia di separazione tra fasi diverse non ci sarà
nessun accumulo di quantità di moto e di energia termica. Le relazioni (6.37)-(6.40) stabiliscono
pertanto le condizioni che devono sussistere affinché all’interfaccia di separazione non si abbia
accumulo di materia, quantità di moto o energia termica.
Inoltre, nel Capitolo 4 abbiamo visto che all’interfaccia I si creano quelle che abbiamo
chiamato condizioni di equilibrio di fase, descritte da una relazione generale del tipo:
Ci( ) K i Ci( )
I
(6.41)
I
la quale stabilisce il legame tra la concentrazione molare della specie chimica i nella fase in
corrispondenza della superficie I, con la concentrazione della stessa specie chimica nella fase
sempre in corrispondenza della superficie di separazione. Espressioni analoghe per l’equilibrio di
fase tra le concentrazioni massiche, le frazioni massiche o quelle molari possono essere scritte in
analogia alla (6.41). Si ricordino a questo proposito le relazioni di equilibrio di fase riportate nel
Capitolo 4.
Cosi come per il trasferimento di materia, condizioni di equilibrio all’interfaccia di
separazione si instaurano anche per quanto riguarda il trasferimento di quantità di moto e di energia
termica. In particolare, si ha che:
v ( ) v ( )
I
(6.42)
I
e
19
T ( ) T ( )
I
(6.43)
I
La condizione (6.41) stabilisce che la velocità in corrispondenza della superficie di
separazione I deve essere uguale nelle due fasi a contatto. Per chiarire meglio questo concetto si
consideri la Figura 6.5, dove è rappresentato il profilo di velocità di un fluido che scorre all’interno
di un tubo cilindrico.
Figura 6.5 Flusso di quantità di moto e distribuzione delle velocità nel moto di un fluido all’interno
di un tubo cilindrico.
La condizione (6.42) fa si che in corrispondenza della superficie di separazione tra la parete
solida del tubo e il fluido, la velocità di quest’ultimo sia nulla in quanto è nulla la velocità con cui si
muove la parete solida. Un altro esempio è mostrato in Figura 6.6 dove sono rappresentati due fluidi
incomprimibili e immiscibili che si muovono tra due piastre piane.
Figura 6.6 Moto di due fluidi immiscibile tra due piastre piane.
20
In questa particolare situazione, la condizione (6.42) determina l’uguaglianza delle velocità
dei due fluidi in corrispondenza della superficie di separazione.
Per quanto riguarda invece il trasferimento di energia termica, la condizione (6.43) stabilisce
che la temperatura delle due fasi in corrispondenza della superficie di separazione siano uguali,
ovvero che su I ci sia la condizione di equilibrio termico.
Prima di concludere la trattazione di questo argomento può essere utile evidenziare come
almeno dal punto di vista formale esiste una analogia nella descrizione del trasferimento di materia
e di energia termica tra le fasi. Nel Capitolo 4 abbiamo visto come il trasferimento di materia può
essere espresso mediante una relazione del tipo:
J i kc Ci* Ci
(6.44)
o similare, la quale ci dice che il trasferimento di materia per effetto di un fenomeno di trasporto
materia di tipo molecolare (diffusione) è data dal prodotto di un coefficiente di trasferimento (in
questo caso di materia) per la differenza tra la concentrazione di equilibrio all’interfaccia e la
concentrazione media all’interno della fase in cui sta avvenendo il trasporto di materia. In maniera
formalmente analoga alla (6.44) è possibile esprimere il trasferimento di energia termica (calore)
per conduzione (fenomeno di trasporto di energia termica di tipo molecolare) come segue:
qc h T I T
(6.45)
la quale esprime il flusso conduttivo come il prodotto del coefficiente di trasferimento di calore per
la differenza tra la temperatura all’interfaccia e la temperatura media all’interno della fase in cui sta
avvenendo il trasferimento di calore.
Inoltre, si è visto come il coefficiente di trasferimento di materia kc è determinato mediante il
numero di Sherwood Sh:
Sh
k c L*
Di
(6.46)
il quale a sua volta è dato da una relazione del tipo:
Sh f (Re, Sc)
(6.47)
21
In maniera analoga, è possibile determinate anche il coefficiente di trasferimento di calore h
mediante un numero adimensionale detto numero di Nusselt Nu, così espresso:
Nu
hL*
k
(6.48)
dove anche in questo caso L* rappresenta la lunghezza caratteristica del sistema. Il numero di
Nusselt a sua volta può essere ricavato mediante relazioni del tipo:
Nu f (Re, Pr)
(6.49)
dove Pr indica un numero adimensionale detto numero di Prandtl, la cui espressione è la seguente:
Pr
C p
(6.50)
22