www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problemi di Fisica
Elettromagnetismo
Il Campo Elettrico
Problema
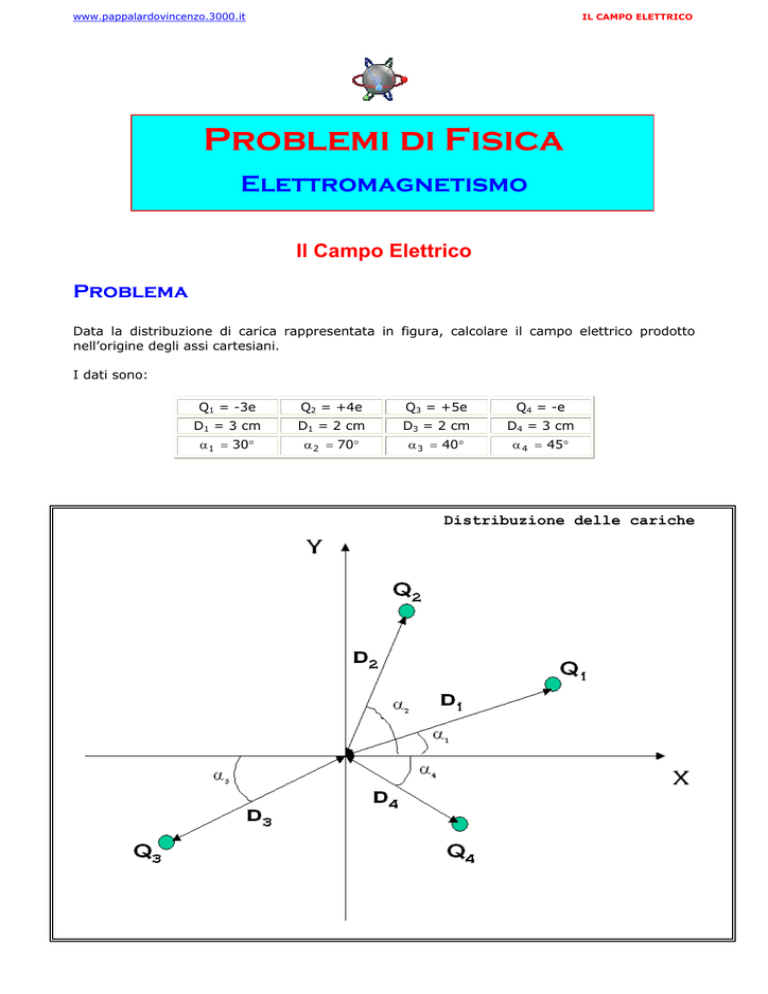
Data la distribuzione di carica rappresentata in figura, calcolare il campo elettrico prodotto
nell’origine degli assi cartesiani.
I dati sono:
Q1 = -3e
Q2 = +4e
Q3 = +5e
Q4 = -e
D1 = 3 cm
D1 = 2 cm
D3 = 2 cm
D4 = 3 cm
α 1 = 30°
α 2 = 70°
α 3 = 40°
α 4 = 45°
Distribuzione delle cariche
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Soluzione
Le quattro cariche generano nell’origine degli assi i vettori campo elettrico E1, E2, E3, E4,
rispettivamente. Dobbiamo quindi trovare modulo e direzione di questi quattro vettori.
Per trovare i moduli applichiamo la definizione di campo elettrico:
Q1
= 9 ⋅ 109 ⋅
(3 ⋅ 10 )
Q2
= 9 ⋅ 109 ⋅
4e
E1 = K ⋅
E2 = K ⋅
D12
D22
E3 = K ⋅
E4 = K ⋅
3e
−2 2
(2 ⋅ 10 )
−2 2
Q3
= 9 ⋅ 109 ⋅
Q4
= 9 ⋅ 109 ⋅
D23
D24
9 ⋅ 109 ⋅ 3 ⋅ 1,6 ⋅ 10−19
=
=
5e
(2 ⋅ 10 )
−2 2
9 ⋅ 109 ⋅ 4 ⋅ 1,6 ⋅ 10−19
4 ⋅ 10− 4
=
e
(3 ⋅ 10 )
9 ⋅ 10− 4
−2 2
9 ⋅ 109 ⋅ 5 ⋅ 1,6 ⋅ 10−19
=
4 ⋅ 10− 4
9 ⋅ 109 ⋅ 1,6 ⋅ 10−19
9 ⋅ 10
−4
= 4,8 ⋅ 10−6 N / C
= 14,4 ⋅ 10−6N / C
= 18 ⋅ 10−6 N / C
= 1,6 ⋅ 10−6 N / C
Ora dobbiamo trovare l’orientamento dei quattro vettori campo elettrico nell’origine, tenendo
presente che per una carica positiva il vettore campo elettrico è un vettore uscente dalla
carica, mentre per una carica negativa è un vettore entrante nella carica.
L’orientamento dei vettori è riportato nel seguente diagramma, dove abbiamo anche trovato
graficamente il vettore campo elettrico totale agente nell’origine:
Diagramma del campo elettrico
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Adesso possiamo trovare le componenti di ciascun vettore su ogni asse e quindi le componenti
del vettore campo elettrico totale ET:
Componenti di E1
Componenti di E2
E1X = E1 ⋅ cos α 1 = 4,8 ⋅ 10 −6 ⋅ cos 30° = 4,2 ⋅ 10 −6 N / C
E2X = E2 ⋅ cos α 2 = 14,4 ⋅ 10 −6 ⋅ cos 70° = 4,9 ⋅ 10 −6 N / C
E1Y = E1 ⋅ senα 1 = 4,8 ⋅ 10 − 6 ⋅ sen30° = 2,4 ⋅ 10 − 6 N / C
E2 Y = E2 ⋅ senα 2 = 14,4 ⋅ 10 − 6 ⋅ sen70° = 13,5 ⋅ 10 − 6 N / C
Componenti di E3
Componenti di E4
E3X = E3 ⋅ cos α 3 = 18 ⋅ 10 −6 ⋅ cos 40° = 13,8 ⋅ 10 −6 N / C
E 4X = E 4 ⋅ cos α 4 = 1,6 ⋅ 10 −6 ⋅ cos 45° = 1,1 ⋅ 10 −6 N / C
E3Y = E3 ⋅ senα 3 = 18 ⋅ 10 − 6 ⋅ sen40° = 11,6 ⋅ 10 − 6 N / C
E 4 Y = E 4 ⋅ senα 4 = 1,6 ⋅ 10 − 6 ⋅ sen45° = 1,1 ⋅ 10 − 6 N / C
E XT =
∑E
X
= E1X − E 2X + E3X + E 4X = 4,2 ⋅ 10 −6 − 4,9 ⋅ 10 −6 + 13,8 ⋅ 10 −6 + 1,1 ⋅ 10 −6 = 14,2 ⋅ 10 −6 N / C
E YT =
∑E
Y
= E1Y − E2 Y + E3Y − E 4 Y = 2,4 ⋅ 10 −6 − 13,5 ⋅ 10 −6 + 11,6 ⋅ 10 −6 − 1,1 ⋅ 10 −6 = −0,6 ⋅ 10 −6 N / C
Per ottenere il modulo di ET ci serviremo del teorema di Pitagora e per ottenere la sua
orientazione utilizzeremo la definizione di tangente:
E T = E2XT + E2YT =
(14,2 ⋅ 10 ) + (− 0,6 ⋅ 10 )
−6 2
−6 2
=
202 ⋅ 10 − 12 + 0,36 ⋅ 10 − 12 =
= 0,014 ⋅ 10 − 6 N / C
tgα =
E YT
− 0,6 ⋅ 10 −6
= −0,04
=
E XT
14,2 ⋅ 10 − 6
α = arctgα = −2,3°
202,4 ⋅ 10 − 12 =
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Una sfera conduttrice di raggio r = 10 cm inizialmente con velocità v0 = 1 m/s, entra in una
regione di spazio dove è presente un campo elettrostatico uniforme E = 100 V/m.
Calcolare il tempo che la sfera impiega a fermarsi se la sua massa è m = 10 g e la
sua densità superficiale σ = 10-6 C/m2
Soluzione
Si tratta di un moto uniformemente accelerato, per cui vale la seguente legge:
(1) v = v 0 − at
Sapendo che:
a=
F
m
F = q⋅E
q = 4πr 2 σ
la (1) diventa:
v = v0 −
F
qE
4πr 2 σE
t = v0 −
t = v0 −
t
m
m
m
da cui ricaviamo l’incognita tempo, tenendo presente che v = 0 (la sfera si ferma dopo un
tempo t):
t =
mv 0
2
4πr σE
=
0,01 ⋅ 1
4π ⋅ 0,12 ⋅ 10 − 6 ⋅ 100
= 796s
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Tra due lastre caricate di segno opposto esiste un campo elettrico uniforme. Un elettrone viene
lasciato libero sulla superficie della lastra carica negativamente e colpisce la superficie della
lastra opposta, a distanza di 20 cm, in un tempo t = 1,5·10-8 s.
Calcolare il campo elettrico tra le due armature.
Soluzione
Per definizione il campo elettrico è dato da:
G
G F
E=
q
ed è diretto dall’armatura positiva a quella negativa.
Mentre la forza F = ma è diretta nel verso opposto in quanto la carica su cui
agisce è un elettrone (e = 1,602·10-19C; m = 9,108·10-31kg), ossia una carica
di segno negativo.
Pertanto, essendo un moto uniformemente accelerato (con a < 0), dalla legge del moto
ricaviamo l’accelerazione:
s=
2s
2 ⋅ 0,2
1 2
at ⇒ a = 2 =
= 0,18 ⋅ 1016 m / s 2
2
t
(1,5 ⋅ 10 − 8 )2
per cui:
F = 9,108 ⋅ 10 −31 ⋅ 0,18 ⋅ 1016 = 1,64 ⋅ 10 −15 N
Infine, il campo elettrico tra le due armature sarà:
E=
1,64 ⋅ 10 −15
1,602 ⋅ 10 − 19
= 1,02 ⋅ 10 4 N / C
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Due gusci sferici conduttori concentrici hanno raggi R1 = 0,145 m e R2 = 0,207 m. La sfera
interna reca una carica Q1 = -6,00·10-8 C. Un elettrone (e = 1,602·10-19C; m = 9,108·10-31kg)
sfugge dalla sfera interna con velocità trascurabile. Supponendo che tra le due sfere ci sia il
vuoto, calcolare con quale velocità l’elettrone colpisce la sfera esterna.
Soluzione
La sfera interna genera un campo elettrico pari a:
E1 = K ⋅
Q1
R 12
= 9 ⋅ 10 9 ⋅
6,00 ⋅ 10 −8
0,145 2
= 25714 N/C
per cui sull’elettrone che sfugge dalla superficie della sfera interna
agirà una forza pari a:
Fe = q ⋅ E = 1,602 ⋅ 10 −19 ⋅ 25714 = 4,1 ⋅ 10 −15 N
con una conseguente accelerazione, per la 2a legge della dinamica, data da:
a=
F
4,1 ⋅ 10 −15
=
= 0,45 ⋅ 1016 m / s 2
m 9,108 ⋅ 10 − 31
In un moto accelerato, la velocità è legata all’accelerazione dalla relazione:
v =
2as
per cui, nel nostro caso, la velocità con la quale l’elettrone colpisce la sfera esterna è:
v =
2a ⋅ (R 2 − R 1 ) =
2 ⋅ 0,45 ⋅ 1016 ⋅ (0,207 − 0,145) = 0,24 ⋅ 10 8 m / s
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Un condensatore piano ha un campo elettrico E = 104 V/m e una lunghezza L = 5 cm. Un
elettrone entra tra le armature con una velocità v0 = 107 m/s ortogonale ad E.
Calcolare l’angolo di deflessione all’uscita del condensatore ed il modulo della velocità
(trascurare gli effetti al bordo).
Soluzione
Dalla definizione di campo elettrico ricaviamo che la forza elettrostatica che agisce
sull’elettrone è data da:
G
G
F = q⋅E
per cui F ha la stessa direzione di E ma verso opposto in
quanto la carica q è negativa. Pertanto F agisce
perpendicolarmente alla velocità iniziale dell’elettrone v0
e lo devia verso destra.
Il moto dell’elettrone in queste condizioni è paragonabile
a quello di un proiettile, cioè costituito da due moti
indipendenti:
moto rettilineo uniforme lungo l’asse y
y = v 0y ⋅ t
(1)
moto uniformemente accelerato lungo l’asse x
vx = a ⋅ t
Ricavando il tempo t dalla (1):
t =
L
v 0y
(2)
e sostituendolo nella (2) otteniamo la componente
x della velocità:
vx = a ⋅
dove a =
L
F
L
e⋅E L
1,6 ⋅ 10 −19 ⋅ 10 4 5 ⋅ 10 −2
=
⋅
=
⋅
=
⋅
= 8,8 ⋅ 10 6 m/s
7
− 31
v 0y
m v 0y
m v 0y
9,11 ⋅ 10
10
F
(2° principio della dinamica).
m
Pertanto il modulo della velocità e l’angolo di deflessione sono dati da:
v Fin =
v 2x + v 2y = (8,8 ⋅ 10 6 )2 + (10 7 )2 = 1,33 ⋅ 10 7 m/s
tgα =
vy
vx
=
10 7
8,8 ⋅ 10 6
= 1,14 ⇒ α = 48,7°
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Due superfici piane distano tra loro d = 0,5 cm e portano ciascuna una carica elettrica di
densità superficiale pari a +σ e –σ. Un elettrone le attraversa perpendicolarmente (si trascuri
la deviazione subita dall’elettrone). L’elettrone oltrepassa la superficie carica negativamente
con velocità v1 = 1,0·105 m/s e quella carica positivamente con velocità v2 = 1,0·106 m/s.
Calcolare il valore della densità
superficiale σ
Cosa succede all’elettrone se entra dalla
parte della superficie carica
positivamente?
Spiegare cosa succede se al posto
dell’elettrone poniamo un protone.
Soluzione
1. Dalla definizione di campo elettrico ricaviamo che la forza elettrostatica che agisce
sull’elettrone è data da:
G
G
F = q⋅E
(1)
per cui F ha la stessa direzione di E ma verso opposto in quanto la carica q è negativa.
La densità superficiale è data come formula inversa del campo elettrico di un condensatore
piano:
E=
σ
⇒ σ = E ⋅ ε0
ε0
Ma il campo elettrico non è noto, per cui dalla (1) si ricava che:
E=
F
e
pertanto il problema si riduce al calcolo della forza elettrica che agisce sull’elettrone.
Dal 2° principio della dinamica sappiamo che:
F = m⋅a
dove l’accelerazione viene calcolata attraverso l’utilizzo delle leggi che regolano il moto
uniformemente accelerato:
v 2 − v1
⎧
⎪⎪a =
t
⎨
⎪d = v t + 1 at 2
1
⎪⎩
2
Il sistema ottenuto è così costituito da due equazioni in altrettante incognite a e t, pertanto:
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
v − v1
⎧
v 2 − v1
⎧
a= 2
v 2 − v1
v 2 − v1
v 2 − v1
⎧
⎧
⎧
⎪
⎪⎪a =
t
⎪a =
⎪a =
⎪a =
⎪
t
⇒ ⎨
⇒ ⎨
⇒ ⎨
⇒ ⎨
t
t
t
⎨
2
d
⎪(v + v )t = 2d
⎪v t + v t = 2d
⎪2d = 2v t + v t − v t
⎪d = v t + 1 ⋅ v 2 − v 1 ⋅ t 2/
⎪t =
1
2
1
1
2
1
2
⎩
⎩
⎩
1
⎪⎩
v1 + v 2
2
t/
⎩⎪
⎧
1 ⋅ 10 6 − 1 ⋅ 10 5
= 0,1 ⋅ 1015 m / s 2
⎪a =
−9
9,1 ⋅ 10
⎪
⎨
2 ⋅ 0,5 ⋅ 10 − 2
⎪
= 9,1 ⋅ 10 − 9 s = 9,1ns
⎪t =
5
6
1 ⋅ 10 + 1 ⋅ 10
⎩
Nota l’accelerazione, siamo in grado di calcolare la forza elettrica F, il campo elettrico E e
quindi la densità superficiale σ:
F = m ⋅ a = 9,1 ⋅ 10 −31 ⋅ 0,1 ⋅ 1015 = 0,9 ⋅ 10 −16 N
E=
F
0,9 ⋅ 10 −16
=
= 0,56 ⋅ 10 3 N / C
e 1,6 ⋅ 10 − 19
σ = E ⋅ ε 0 = 0,56 ⋅ 10 3 ⋅ 8,86 ⋅ 10 −12 = 5 ⋅ 10 −9 C / m2 = 5nC / m2
In maniera alternativa, e più convincente, possiamo calcolare la forza che agisce sulla carica
attraverso l’utilizzo del teorema dell’energia cinetica, che stabilisce:
la variazione di energia cinetica della particella è uguale al lavoro compiuto dalle forze del
campo sulla particella:
L = ∆E c =
(
)
[
]
1
1
1
1
mv 22 − mv 12 = m ⋅ v 22 − v 12 = ⋅ 9,1 ⋅ 10 − 31 ⋅ (10 6 )2 − (10 5 )2 = 4,5 ⋅ 10 − 19 J
2
2
2
2
Dalla definizione di lavoro ricaviamo la forza che agisce sulla particella:
L =F⋅d⇒F =
L
4,5 ⋅ 10 −19
=
= 9 ⋅ 10 − 17 N
d
0,5 ⋅ 10 − 2
per cui possiamo calcolare il campo elettrico e quindi la densità di carica superficiale:
E=
F
9 ⋅ 10 −17
=
= 0,56 ⋅ 10 3 N / C
e 1,6 ⋅ 10 − 19
σ = E ⋅ ε 0 = 0,56 ⋅ 10 3 ⋅ 8,86 ⋅ 10 −12 = 5 ⋅ 10 −9 C / m2 = 5nC / m2
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
2. Se l’elettrone entra dalla parte della superficie
carica positivamente, sempre in base alla legge
(1), avremo che la particella, essendo carica
negativamente, sarà sottoposta ad una forza che
avrà verso opposto al campo elettrico, per cui
subirà un rallentamento.
3. Se al posto dell’elettrone poniamo un protone, in base alla legge (1), avremo che la
particella, essendo carica positivamente, subirà una decelerazione se entrerà dalla parte
della superficie carica negativamente (vedi figura), e una accelerazione se entrerà dalla
parte della superficie carica positivamente (vedi figura).
I calcoli da eseguire al punto 2. e al punto 3. sono gli stessi di quelli eseguiti al punto 1.
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Determinare il punto nel quale una goccia carica d’inchiostro tocca il foglio di carta. I dati del
problema sono:
m = 1,3 · 10-10 kg
Q = -1,5 · 10-13 C
Vx = 18 m/s
L = 1,6 cm
E = 1,4 · 106 N/C
Soluzione
La goccia viene caricata negativamente nell’apposito dispositivo ed entra con una velocità Vx
tra i piatti deflettenti, dove viene deflessa verso l’alto dalla presenza del campo elettrico E
diretto verso il basso, infatti:
F = Q · E = -1,5 · 10-13 · 1,4 · 106 = -2,1 · 10-7 N
La presenza di F, grazie al secondo principio della dinamica, comporta una accelerazione
anch’essa verso l’alto:
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
F = m ⋅ ay ⇒ ay =
F
− 2,1 ⋅ 10 −7
=
= −1,6 ⋅ 10 3 m / s 2
− 10
m
1,3 ⋅ 10
Pertanto:
lungo l’asse X il moto della goccia è rettilineo uniforme, per cui la legge del moto è:
1) L = Vx · t
lungo l’asse Y il moto è uniformemente accelerato, per cui la legge del moto è:
2) y =
1
g ⋅ t2
2
Ricavando t dalla 1):
t=
L
1,6 ⋅ 10−2
=
= 0,09 ⋅ 10−2 s
Vx
18
E sostituendola nella 2), otteniamo il punto nel quale la goccia tocca il foglio di carta:
y=
1
⋅ 9,8 ⋅ (0,09 ⋅ 10−2 )2 = 6,5 ⋅ 10−5 = 0,65mm
2
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Data la distribuzione di carica in figura, determinare il flusso del campo elettrico attraverso la
superficie S.
I dati sono:
Q1 = Q4 = + 3,1 nC
Q2 = Q5 = -5,9 nC
Q3 = -3,1 nC
Q6 = neutra
S
Q1+
Q4+
Q3-
-
Q2
Q6neutra
Q5-
Soluzione
Il flusso del campo elettrico attraverso la superficie S, che chiameremo superficie gaussiana, si
calcola attraverso la legge di Gauss:
G
Φ(E) =
∑
Q int erna
ε0
=
Q1 + Q 2 + Q 3
N ⋅ m2
+ 3,1 ⋅ 10 − 9 − 5,9 ⋅ 10 − 9 − 3,1 ⋅ 10 − 9
670
=
−
=
ε0
C
8,85 ⋅ 10 − 12
Notare:
•
•
•
La carica neutra non dà nessun contributo al flusso, anche se è inclusa nella superficie S
Le cariche Q4 e Q5 non danno nessuno contributo al flusso perché sono esterne alla
superficie S e non sono perciò incluse in ΣQinterna
Il segno meno indica che la carica netta all’interno della superficie S è negativa e che il
flusso attraverso S è entrante.
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
La parte visibile di un fulmine è preseduta da una fase invisibile in cui una colonna di elettroni
si estende da una nuvola verso terra. Questi elettroni provengono dalla nuvola e dalle molecole
dell’aria ionizzate all’interno della colonna. La densità di carica lineare lungo la colonna è
tipicamente λ = -1 · 10-3 C/m. Quando la colonna raggiunge la terra, gli elettroni contenuti in
essa vengono scaricati rapidamente a terra. Durante la scarica, le collisioni tra gli elettroni e
l’aria della colonna danno luogo ad un lampo brillante di luce. Se le molecole d’aria si ionizzano
quando l’intensità di campo elettrico è E = 3 · 106 N/C, qual è il raggio della colonna?
Soluzione
Per risolvere questo problema, facciamo prima delle considerazioni di carattere generale. Sia
data una bacchetta di plastica, carica, infinitamente
lunga, con una densità di carica λ uniforme.
Troviamo il campo elettrico ad una distanza R
dall’asse della bacchetta, utilizzando il teorema di
Gauss.
La scelta della superficie gaussiana dovrebbe
adattarsi alla simmetria del problema, che è
cilindrica, per cui scegliamo un cilindro circolare di
raggio R e lunghezza h, coassiale con la bacchetta.
Attraverso la superficie laterale SL il flusso è dato da:
G
G G
Φ(E) = E • S = E ⋅ SL ⋅ cos α = E ⋅ S = E ⋅ (2πR ⋅ h)
Notare :
•
α = 0° tra E
SL = 2πR ⋅ h
ed
S
⇒ cos 0° = 1
Attraverso le basi del cilindro il flusso è nullo perché:
α = 90° tra E
ed
S
G
⇒ cos 0° = 1 ⇒ Φ(E) = 0
In definitiva, applicando il teorema di Gauss, otteniamo:
G
Φ(E) =
∑Q
ε0
int
⇒ E ⋅ 2πR ⋅ h =
λ ⋅h
λ
⇒E=
ε0
2πε 0 ⋅ R
(1)
dove: Qint = λ ⋅ h
Ritorniamo al nostro problema, e sebbene la colonna non sia rettilinea né infinitamente lunga,
si può considerare approssimativamente una carica lineare.
Per trovare il raggio della colonna, risolviamo la (1) rispetto ad R:
R=
λ
1 ⋅ 10 −3
=
= 6m
2πε 0 ⋅ E 2π ⋅ 8,85 ⋅ 10 −12 ⋅ 3 ⋅ 106
Notare
•
•
Il campo elettrico E si dirige radialmente verso l’interno poiché la colonna è fatta di
elettroni
Sebbene la colonna possa essere soltanto di 6 m di raggio, non si creda di essere al
sicuro se ci si trova ad una distanza maggiore dal punto d’impatto del fulmine, perché gli
elettroni trasportati dal fulmine si propagano sul terreno e queste correnti di terra sono
letali.
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Un pendolino elettrico di massa m = 4,0 g e carica q = 0,20 µF si trova in equilibrio nel campo
elettrico generato da un filo carico infinitamente lungo, la cui densità lineare di carica è λ =
4,0·10-5 C/m.
Se all’equilibrio la distanza della sferetta del pendolino dal filo carico è r = 1,5 m e il pendolino
è deviato di un angolo θ rispetto alla verticale, calcolare:
1. l’intensità del campo elettrico
2. l’intensità T della tensione del filo e l’ampiezza dell’angolo θ
Soluzione
1. Si dimostra che l’intensità
infinitamente lungo è data da:
E=
di
un
filo
λ
2πε 0r
Sostituendo i dati del problema otteniamo:
E=
4,0 ⋅ 10 −5
2π ⋅ 8,85 ⋅ 10
− 12
⋅ 1,5
= 4,8 ⋅ 105 N/C
2. Come si vede dalla figura, sulla sferetta
agiscono la forza elettrica Fe = qE, la forza peso
P = mg e la tensione T del filo.
Essendo il pendolino in equilibrio, applichiamo la condizione d’equilibrio alla carica q:
G
G
∑F = 0 ⇒ F
e
G G
+P+ T = 0
(1)
Fissato un sistema di assi cartesiani, scomponiamo la (1) secondo gli assi e otteniamo un
sistema di due equazioni nelle incognite T e θ :
⎧qE − T sin ϑ = 0
⎨
⎩T cos ϑ − mg = 0
Il sistema ammetterà le seguenti soluzioni:
tgϑ =
qE
0,20 ⋅ 10 −6 ⋅ 4,8 ⋅ 10 5
=
= 2,45 ⇒ ϑ = 68°
mg
4,0 ⋅ 10 − 3 ⋅ 9,81
T =
mg
4,0 ⋅ 10 −3 ⋅ 9,81
=
= 0,10 N
cos ϑ
cos 68
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Determinare il campo elettrico generato in ogni punto dello spazio da una sfera conduttrice
omogenea di raggio R elettrizzata con una carica Q
Soluzione
In condizioni di equilibrio elettrostatico il campo elettrico, in base al teorema di Gauss, è nullo
in tutti i punti interni alla sfera.
Inoltre sappiamo che la carica elettrica di un conduttore si distribuisce interamente sulla sua
superficie. In particolare, avendo a che fare con una sfera conduttrice, ossia con un conduttore
di forma simmetrica, la carica Q si disporrà sulla superficie in maniera uniforme.
Si tratta, dunque, di una distribuzione superficiale di carica a simmetria sferica, il cui campo
elettrico esterno coincide con quello di una carica puntiforme Q posta nel centro.
Per punti esterni alla sfera (r > R) il campo è diretto
radialmente (verso uscente se Q è positiva, entrante se Q
negativa) e il suo modulo è:
E=K⋅
Q
r2
ossia il campo decresce come 1/r2 a partire dal valore
Q
massimo Emax = K ⋅ 2 raggiunto sulla superficie della
R
sfera (r = R)
Per punti interni alla sfera (r < R) il campo è nullo.
Problema
Quattro cariche puntiformi sono disposte nei vertici di un quadrato come in figura. Dopo aver
eseguito una rappresentazione in scala dei campi generati dalle singole cariche nel centro del
quadrato, determinare il campo elettrico totale.
(Q1 = +3 · 10-10 C
Q2 = +6 · 10-10 C
Q3 = +6 · 10-10C
Q
4
= -2 · 10-10C
Soluzione
Q1
Q2
E3
D
L
E1
E4
E2
ET
Q3
Q4
L = 10 cm)
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
La distanza di ciascuna carica dal centro del quadrato è pari alla metà della diagonale del
quadrato, che si calcola applicando il teorema di Pitagora al triangolo di lato L:
D = L2 + L2 =
2L2 = L ⋅ 2 = 0,1 ⋅ 2 = 0,14m ⇒
D
= 0,07m
2
Il campo elettrico prodotto da ciascuna carica nel centro del quadrato è dato da:
E1 = K ⋅
E3 = K ⋅
Q1
⎛D⎞
⎜ ⎟
⎝2⎠
2
Q3
⎛D⎞
⎜ ⎟
⎝2⎠
2
= 9 ⋅ 10 9 ⋅
= 9 ⋅ 10 9 ⋅
3 ⋅ 10 −10
(0,07)
2
6 ⋅ 10 −10
(0,07)
2
= +5,5 ⋅ 10 2 N / C
= +11 ⋅ 10 2 N / C
E2 = K ⋅
E4 = K ⋅
Q2
⎛D⎞
⎜ ⎟
⎝2⎠
Q4
⎛D⎞
⎜ ⎟
⎝2⎠
2
2
= 9 ⋅ 10 9 ⋅
= 9 ⋅ 10 9 ⋅
6 ⋅ 10 −10
(0,07)
2
= +11 ⋅ 10 2 N / C
(−2 ⋅ 10 −10 )
(0,07)
2
= −3,7 ⋅ 10 2 N / C
A questo punto siamo in grado di riportare in scala i singoli campi elettrici e determinare
graficamente il campo elettrico totale prodotto nel centro del quadrato. Come si vede dalla
figura, i campi elettrici E2 e E3 sono uguali ed opposti, quindi si annullano, mentre E1 e E2 sono
concordi e quindi si possono sommare. Pertanto il campo elettrico totale è dato da:
E T = E1 + E 4 = 5,5 ⋅ 10 2 + 3,7 ⋅ 10 2 = 9,2 ⋅ 10 2 N / C
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Due cariche puntiformi Q1 = 20 µC e Q2 = -40µC distano 1 m l’una dall’altra. Determinare il
punto sulla retta individuata dalle due cariche in cui il campo elettrico è nullo.
Soluzione
Innanzitutto stabiliamo da che parte è situato il punto:
Q1
E2
E1
+
B
A
E1
Q2
E2
-
E2
E1
C
L
x
Tenendo presente la definizione di campo elettrico, valgono le seguenti considerazioni:
se il punto fosse C, in esso agirebbero due campi elettrici opposti, ma E2 sarebbe più
grande di E1 in quanto la carica Q2, oltre ad essere più vicina al punto C, ha un valore più
grande della carica Q1;quindi nel punto C il campo elettrico totale non può essere nullo;
se il punto fosse in B, su di esso agirebbero due campi elettrici concordi, per cui in B il
campo elettrico totale non può essere nullo;
se il punto fosse A, su di esso agirebbero due campi elettrici opposti, ed essendo la
carica Q2 più lontana, la posizione A sarà quella in cui il campo elettrico totale è nullo.
La condizione per cui nel punto A il campo elettrico totale sia nullo è la seguente:
(1) E1 - E2 = 0
Se fissiamo l’origine dell’asse X nel punto A e indichiamo con x la posizione del punto A
rispetto a Q1, la (1) diventa:
K/ ⋅
Q1
x
2
= K/ ⋅
Q2
2
(x + L)
⇒
20 ⋅ 10 −6
x
2
=
40 ⋅ 10 −6
2
(x + L)
⇒
1
x
2
=
2
(x + L)2
⇒ (x + L)2 = 2x 2
x 2 + 2x ⋅ L + L2 − 2x 2 = 0 ⇒ −x 2 + 2x ⋅ L + L2 = 0 ⇒ x 2 − 2x ⋅ L − L2 = 0 ⇒ x 2 − 2x − 1 = 0
L’equazione da risolvere è un’equazione di 2° grado le cui soluzioni sono:
x =
− b ± b 2 − 4ac
2± 4+4
2 ± 2.8
2 + 2.82
2 − 2.8
=
=
⇒ x1 =
= 2.41m ⇒ x 2 =
= −0.4m
2a
2
2
2
2
Per come abbiamo fissato l’asse X, la soluzione x2 è da scartare per cui la soluzione del
problema è:
x2 = 2.41 m
il campo elettrico è nullo all’esterno del segmento individuato dalle due cariche a 2,41 m di
distanza da Q1.
X
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Determinare in quale punto P, compreso tra due cariche, il campo elettrico è nullo. In dati
sono:
Q1 = + 1,5 · 10-7 C
Q2 = + 3,5 · 10-7 C
d = 70 cm = 0,7 m
Soluzione
Rappresentiamo la situazione descritta dal problema:
Q1
P
E2
E1
++
Q2
+
X
d-x
x
d
La condizione per cui nel punto P il campo elettrico totale sia nullo è la seguente:
(1) E1 = E2
Se fissiamo l’origine dell’asse X nella carica Q1 e indichiamo con x la distanza di Q1 rispetto a P
e con (d – x) la distanza di Q2 rispetto a P, la (1) diventa:
K/ ⋅
Q1
x
2
= K/ ⋅
Q2
2
(d − x)
2
⇒
1,5 ⋅ 1/ 0/ −7
x
2
=
3,5 ⋅ 1/ 0/ −7
2
(d − x)
⇒ 1,5 ⋅ (d − x)2 = 3,5 ⋅ x2 ⇒ 1,5 ⋅ (0,7 − x)2 = 3,5 ⋅ x 2 ⇒
2
1,5 ⋅ (0,49 + x − 1,4x) = 3,5x ⇒ 0,74 + 1,5x2 − 2,1x = 3,5x2 ⇒ 2x 2 + 2,1x − 0,74 = 0
L’equazione da risolvere è un’equazione di 2° grado le cui soluzioni sono:
x =
− 2,1 ± 4,4 + 5,9
− b ± b 2 − 4ac
− 2,1 ± 3,2
− 2,1 + 3,2
− 2,1 − 3,2
=
=
⇒ x1 =
= 0,28m ⇒ x 2 =
= −1,3m
2a
4
2
4
4
Per come abbiamo fissato le cariche sull’asse X (ricorda che la carica Q1 è nell’origine dell’asse
X), la soluzione x2 è da scartare (perché si riferisce ad un punto che è alla sinistra della carica
Q1), per cui la soluzione del problema è:
x2 = 0,28 m
perché rappresenta la posizione di un punto P compreso tra le due cariche, come richiesto dal
problema.
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Una piccola sfera di plastica di masse m = 3g e carica elettrica q1 = +2µC viene lanciata, alla
velocità v1 = 4 m/s, contro una sfera metallica ferma avente carica elettrica q2 = + 4µC. E
distante d = 4m. Determinare la distanza tra le due sfere nel punto di massimo avvicinamento.
Soluzione
q1
P
V1
x
q2
d
Le due cariche, avendo lo stesso segno, tendono a respingersi; però la carica q1, avendo
un’energia cinetica, riesce a vincere la forza repulsiva e quindi si avvicina alla carica q2 fino alla
posizione P, che rappresenta il punto di massimo avvicinamento. Poiché la forza elettrica è
conservativa, l’energia totale del sistema si conserva durante il movimento:
EC + U = cos tan te ⇒
1
q ⋅q
q ⋅q
mv2 + K ⋅ 1 2 = K ⋅ 1 2
2
d
x
Sostituendo i dati del problema, otteniamo una equazione di 1° grado dove l’incognita è
proprio la posizione di massimo avvicinamento:
1
2 ⋅ 10−6 ⋅ 4 ⋅ 10−6
2 ⋅ 10 −6 ⋅ 4 ⋅ 10−6
0,072
⋅ 3 ⋅ 10−3 ⋅ 16 + 9 ⋅ 109 ⋅
= 9 ⋅ 109 ⋅
⇒ 0,024 + 0,018 =
⇒
2
4
4
x
0,072
0,042x = 0,072 ⇒ x =
= 1,7m
0,042
Problema
Due elettroni distano 2 m. Un altro elettrone, lanciato dall’infinito, si ferma a metà strada tra
essi. Quale deve essere la sua velocità iniziale?
Soluzione
Per il principio di conservazione, l’energia meccanica dell’elettrone proveniente dall’infinito
(cinetica + potenziale), si conserva:
EC + U = costante
ossia:
ECi + Ui = ECf + Uf
Poiché l’elettrone proviene dall’infinito, la sua energia potenziale iniziale è nulla; mentre,
poiché si ferma a metà strada tra i due elettroni, la sua energia cinetica finale è nulla.
Pertanto, il principio di conservazione diventa:
⎛ e2
1
e 2 ⎞⎟
1
4e 2
mv i2 = K ⋅ ⎜
⇒ mv i2 = K ⋅
+
⎜d /2 d /2⎟
2
2
d
⎠
⎝
da cui è possibile ricavare l’incognita vi:
E Ci = U f ⇒
vi =
8Ke 2
=
md
8 ⋅ 9 ⋅ 10 9 ⋅ (1,602 ⋅ 10 − 19 )2
9,108 ⋅ 10 − 31 ⋅ 2
= 32 m/s
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
In un campo elettrico, per trasportare una particella da un punto A a un punto B fra i quali
esiste una differenza di potenziale VAB = 3,0·105 V, la forza del campo elettrico compie un
lavoro L = 4,8·10-14 J.
Supponendo che sulla particella non agiscano altre forze diverse da quella elettrica,
determinare:
la carica della particella
l’aumento dell’energia cinetica
Soluzione
Dalla definizione di differenza di potenziale ricaviamo il valore della carica della particella:
L
L
4,8 ⋅ 10 −14
⇒q=
=
= 1,6 ⋅ 10 − 19 C
q
VAB
3,0 ⋅ 105
Attraverso l’ausilio del teorema dell’energia cinetica determiniamo l’aumento dell’energia
cinetica della carica:
VAB =
∆E = L = 4,8 ⋅ 10 −14 J
Problema
12 elettroni sono posti ugualmente distanziati su un cerchio di raggio R = 1 mm . Rispetto a V
= 0 all'infinito (preso come livello di zero per il potenziale):
1. che valore hanno il potenziale elettrico ed il campo elettrico nel centro C del cerchio
2. discutere qualitativamente la situazione per quanto riguarda il potenziale elettrico
ed il campo elettrico in C nel caso in cui gli elettroni fossero disposti lungo il cerchio
in maniera non uniforme.
Soluzione
1. Poiché tutti gli elettroni hanno la stessa carica negativa e tutti sono disposti alla stessa
distanza R dal centro, il potenziale nel punto C, con l’ausilio del principio di
sovrapposizione, è:
n
V =
∑
i =1
Vi =
1
4πε 0
n
∑
i=
qi
1
e
1,6 ⋅ 10 −19
= −12 ⋅
⋅
= −12 ⋅ 9 ⋅ 10 9 ⋅
= −173 ⋅ 10 − 7 V
ri
4πε 0 R
10 − 3
Poiché il potenziale elettrico è uno scalare, l’orientamento di
ciascuna carica rispetto a C è irrilevante per il potenziale V.
Al contrario, poiché il campo elettrico è un vettore, l’orientamento
degli elettroni è importante per la determinazione di E.
Infatti, il vettore campo elettrico nel punto C, dovuto ad un certo
elettrone, a causa della disposizione simmetrica viene annullato dal
vettore campo elettrico dovuto all’elettrone che si trova
diametralmente opposto. Per cui nel punto C:
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
E=0
2. Se gli elettroni fossero spostati lungo il cerchio fino ad avere
una distribuzione disuniforme, il potenziale sarebbe sempre lo
stesso in quanto ogni elettrone ha sempre la stessa distanza
da C e, come abbiamo detto, l’orientamento è irrilevante.
Invece, il campo elettrico, sempre per ciò che abbiamo detto,
non è più nullo in quanto la disposizione degli elettroni non è
più simmetrica. Pertanto esisterà un campo elettrico netto
risultante diretto verso la maggiore distribuzione di cariche.
Problema
Calcolare il potenziale elettrico nel punto P al centro di un quadrato di lato L = 1,3 m e sui cui
vertici sono collocate quattro cariche puntiformi:
Q1 = + 12 nC
Q2 = - 24 nC
Q3 = + 31 nC
Q4 = + 17 nC
Soluzione
Poiché tutte le cariche hanno la stessa distanza r dal punto P, il
potenziale nel punto P, con l’ausilio del principio di
sovrapposizione, deve essere:
n
V =
∑V
i
i =1
=
1
4πε 0
2
dove: r =
n
qi
i=
i
∑r
⎛L ⎞
⎛L ⎞
⎜ ⎟ +⎜ ⎟
⎝2⎠
⎝2⎠
= 9 ⋅ 10 9 ⋅
2
=
L
2
=
(12 − 24 + 31 + 17) ⋅ 10 −9
= 352 V
0,92
1,3
2
= 0,92 m
Problema
Calcolare il potenziale del campo elettrico di una carica Q = 2,0 µC nel punto P distante 1,0 m.
Quanto vale il lavoro compiuto contro le forze del campo per spostare una carica q = -1,0 µC
dal punto P al punto O che dista 2,0 m da Q.
Soluzione
Applicando la definizione di potenziale elettrico di
una carica puntiforme otteniamo:
V =
1
Q
2,0 ⋅ 10 −6
⋅
= 9 ⋅ 10 9 ⋅
= 18 ⋅ 10 3 V
4πε 0 d
1
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Per trovare il lavoro, possiamo eseguire lo stesso ragionamento applicato al campo
gravitazionale terrestre ponendo le cariche in luogo delle masse e la costante K in luogo di
quella gravitazionale:
L =
Q⋅q
4πε 0
⎛1
1 ⎞
⎛1 1 ⎞
⎟⎟ = 9 ⋅ 10 9 ⋅ 2,0 ⋅ 10 − 6 ⋅ 1,0 ⋅ 10 − 6 ⋅ ⎜ − ⎟ = 9 ⋅ 10 − 3 J
⋅ ⎜⎜ −
d
d
⎝1 2 ⎠
1 ⎠
⎝
Problema
Le cariche elettriche puntiformi Q1 = -40,0 nC e Q2 = +20,0 nC sono separate da una distanza
d = 10,0 m.
Determinare sulla retta passante per le due cariche i punti in cui il potenziale elettrico
è nullo.
Soluzione
Tenendo presente la definizione di
potenziale elettrico di una carica
puntiforme:
V =
1
Q
⋅
4πε 0 r
(1)
notiamo che V1 < 0 in quanto Q1 è negativa e V2 > 0 in quanto Q2 è positiva.
Pertanto il potenziale totale V, che per il principio di sovrapposizione è la somma algebrica dei
singoli potenziali V1 e V2, sarà nullo nei punti in cui V1 e V2 sono uguali in valore assoluto.
Il potenziale V non si può annullare in nessun punto alla sinistra della carica Q1 in quanto in
questi punti V1 è sempre maggiore di V2 visto che dai dati del problema Q1 è maggiore di Q2 e
dalla (1) il potenziale è direttamente proporzionale alla carica ed inversamente proporzionale
alla distanza.
Pertanto il potenziale si potrà annullare solo nei punti più vicini a Q2, e cioè nei punti compresi
tra le due cariche e a sinistra di Q2.
Indichiamo con x l’ascissa di un punto a potenziale nullo e supponiamo che si trovi a destra di
Q2 e applichiamo, quindi, il principio di sovrapposizione:
n
V =
∑V
i
= V1 + V2 = 0 ⇒
i =1
Q
Q2
Q
Q2
1
1
⋅ 1 +
⋅
=0⇒ 1 +
=0
4πε 0 x
4πε 0 x − d
x
x−d
da cui, risolvendo rispetto ad x si ha:
x =
d ⋅ Q1
10,0 ⋅ (−40,0 ⋅ 10 −9 )
=
= 20,0 m
Q1 + Q 2
(−40,0 + 20,0) ⋅ 10 − 9
Vediamo se esiste anche tra le due cariche un punto a potenziale nullo. Indichiamo ancora con
x l’ascissa di tale punto e applichiamo di nuovo il principio di sovrapposizione:
n
V =
∑V
i
i =1
= V1 + V2 = 0 ⇒
Q
Q2
Q
Q2
1
1
⋅ 1 +
⋅
=0⇒ 1 +
=0
4πε 0 x
4πε 0 d − x
x
d−x
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
da cui, risolvendo rispetto ad x si ha:
x =
− d ⋅ Q1
− 10,0 ⋅ (−40,0 ⋅ 10 −9 )
=
= 6,67 m
− Q1 + Q 2
(40,0 + 20,0) ⋅ 10 − 9
In definitiva esistono due punti a potenziale nullo sulla retta passante per le due cariche.
Problema
In un condensatore piano ideale, infinitamente esteso, le due armature possiedono densità
superficiali di carica rispettivamente uguali a +σ e a –σ.
Determinare il campo elettrico all’interno e all’esterno del condensatore.
Soluzione
Per il principio di sovrapposizione, il campo elettrico E in
ogni punto dello spazio è uguale alla somma vettoriale dei
campi elettrici E1 ed E2 generati in quello stesso punto,
separatamente, dalle due armature cariche.
L’armatura a sinistra che possiede una densità superficiale
di carica +σ, produce un campo elettrico E1 diretto
perpendicolarmente alla sua superficie in verso uscente, di
modulo:
E1 =
σ
2ε 0
L'armatura a destra, con densità superficiale –σ, produce
invece un campo elettrico E2 in verso entrante, avente modulo.
E2 = E1
All'esterno del condensatore i due campi elettrici si annullano, per cui il campo risultante ha
modulo:
E=0
Nello spazio compreso fra le due piastre, invece, i due campi hanno verso concorde e quindi i
loro moduli, entrambi uguali a:
E1 = E2 =
σ
2ε 0
si sommano.
In conclusione, dentro al condensatore il campo è uniforme, diretto perpendicolarmente
dall'armatura positiva a quella negativa, con modulo:
E = E1 + E2 =
σ
σ
σ
+
=
2ε 0 2ε 0
ε0
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Una particella di massa m = 2,0 g e carica q = -2,5·105 C si trova in equilibrio nel campo
elettrico uniforme di un condensatore carico.
Calcolare la densità superficiale di carica sulle armature del condensatore.
Soluzione
Il campo elettrico tra le armature piane del condensatore è
dato da:
E=
σ
ε0
da cui ricaviamo la formula per il calcolo della densità
superficiale:
σ = ε 0E
Pertanto il problema si riduce al calcolo del campo elettrico tra le armature del condensatore.
Poiché la particella è in equilibrio nel campo elettrico, le due forze che agiscono su q, la forza
peso P = mg diretta verticalmente verso il basso e la forza elettrica F = -qE diretta
verticalmente verso l’alto, per la condizione di equilibrio, si devono bilanciare, quindi:
qE = mg
da cui ricaviamo il valore del campo elettrico uniforme:
E=
mg 2,0 ⋅ 10 −3 ⋅ 9,81
=
= 7,8 ⋅ 10 − 8 N / C
5
q
2,5 ⋅ 10
Infine, noto il campo elettrico, possiamo calcolare la densità superficiale:
σ = 8,859 ⋅ 10 −12 ⋅ 7,8 ⋅ 10 −8 = 69 ⋅ 10 −20 C / m 2
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Due condensatori di capacità 3 µF e 6 µF rispettivamente sono connessi in serie ed il sistema
così ottenuto è caricato a 500 V. Calcolare la carica su ciascuna armatura e l’energia
immagazzinata da ciascun condensatore.
Soluzione
C1
C2
CE
V
V
Poiché i condensatori sono in serie, sulle loro armature si accumulerà una stessa carica, che è
la stessa che si accumula sul condensatore equivalente:
1
1
1
1 1
1
=
+
= + = 0,5 ⇒ CE =
= 2µF
CE
C1 C2
3 6
0,5
Q = CE ⋅ V = 2 ⋅ 10−6 ⋅ 500 = 1000 ⋅ 10−6 C = 10−3 C
L’energia immagazzinata da ciascun condensatore, sotto forma di energia elettrica, non è altro
il lavoro speso dal generatore per caricare i singoli condensatori:
E1 = L1 =
1 Q2
1 (10−3 )2
⋅
= ⋅
= 0,17J
2 C1
2 3 ⋅ 10−6
E2 = L 2 =
1 Q2
1 (10−3 )2
⋅
= ⋅
= 0,08J
2 C2
2 6 ⋅ 10−6
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Due condensatori di capacità 4µF e 8µF collegati in parallelo sono caricati con una differenza di
potenziale di 100 V. Determinare la carica accumulata sulle armature di ciascun condensatore
e l’energia immagazzinata dal sistema.
Soluzione
C1
CE
C2
V
V
I due condensatori, essendo in parallelo, sono sottoposti alla stessa differenza di potenziale V,
per cui la carica accumulata su di essi è data da:
Q1 = C1 ⋅ V = 4 ⋅ 10 −6 ⋅ 100 = 4 ⋅ 10 −4 C
Q 2 = C 2 ⋅ V = 8 ⋅ 10 − 6 ⋅ 100 = 8 ⋅ 10 − 4 C
Per calcolare l’energia immagazzinata dal sistema, dobbiamo prima calcolare la capacità
equivalente, che nel caso di condensatori in parallelo è data da:
C E = C1 + C 2 = 4 + 8 = 12µF
per cui:
E=L =
1
1
C E V 2 = ⋅ 12 ⋅ 10 − 6 ⋅ 100 2 = 6 ⋅ 10 − 2 J
2
2
Ricorda: l’energia immagazzinata dal sistema sotto forma di energia elettrica è il lavoro speso
dal generatore V per caricare il condensatore equivalente che rappresenta il sistema dei due
condensatori.
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Una sfera metallica di 10 cm di raggio è portata al potenziale di 2·104 V. Determinare la
capacità e la carica della sfera.
Soluzione
Dalla formula del potenziale di un conduttore sferico ricaviamo la carica della sfera:
V =
1 Q
⇒ Q = 4πε 0 ⋅ V ⋅ R = 4π ⋅ 8,86 ⋅ 10 − 12 ⋅ 2 ⋅ 10 4 ⋅ 10 ⋅ 10 − 2 = 223 ⋅ 10 − 9 C
4πε 0 R
La capacità della sfera la calcoliamo attraverso la sua definizione:
C=
Q 223 ⋅ 10−9
=
= 111,5 ⋅ 10−13F = 11,2 ⋅ 10−12F = 11,2pF
4
V
2 ⋅ 10
Problema
Un condensatore piano ha le armature circolari di raggio 10 cm, distanti tra loro 2 cm, e come
dielettrico l’aria. Quanta energia viene immagazzinata dal condensatore se è caricato con una
differenza di potenziale (d.d.p.) uguale a 1000 V?
Soluzione
L’energia immagazzinata da un condensatore è data da:
E=
1
CV 2
2
e per calcolarla dobbiamo prima determinare il valore della capacità. Poiché il problema
fornisce le caratteristiche geometriche e fisiche del condensatore, allora la capacità la
calcoliamo come:
C = ε0
S
3,14 ⋅ 10−2
= 8,86 ⋅ 10−12 ⋅
= 13,9 ⋅ 10−12F = 13,9pF
−2
d
2 ⋅ 10
dove:
S = πR 2 = π ⋅ (10 ⋅ 10 −2 )2 = 3,14 ⋅ 10 −2 m2
In definitiva:
E=
1
⋅ 13,9 ⋅ 10−12 ⋅ 10002 = 7 ⋅ 10−6 J
2
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Un condensatore piano , con le armature di superficie 20,0 cm2 distanti nel vuoto 1,00 mm,
viene caricato con una differenza di potenziale di 1000 V.
Calcolare:
1. la carica accumulata sulle armature
2. l’energia immagazzinata
3. la densità di energia del campo elettrico
Soluzione
1. Poiché sono note le caratteristiche fisiche e geometriche del condensatore, possiamo
calcolare la sua capacità:
C = ε0
S
20,0 ⋅ 10 −4
= 8,859 ⋅ 10 − 12 ⋅
= 17,7 ⋅ 10 − 12 F = 17,7pF
d
1,00 ⋅ 10 − 3
Dalla definizione di capacità ricaviamo la formula per calcolare la carica accumulata sulle
armature:
C=
Q
⇒ Q = C ⋅ V = 17,7 ⋅ 10 − 12 ⋅ 1000 = 17,7 ⋅ 10 − 9 C = 17,7nC
V
2. Il lavoro speso per caricare il condensatore è immagazzinato sotto forma di energia
potenziale elettrica, per cui:
E=L =
1
1
QV = ⋅ 17,7 ⋅ 10 − 9 ⋅ 1000 = 8,85 ⋅ 10 − 6 J = 8,85µJ
2
2
3. Poiché fra le armature del condensatore esiste un campo elettrico che si annulla quando il
condensatore si scarica, possiamo anche pensare che l’energia spesa dal generatore per
caricare il condensatore venga immagazzinata nel campo elettrico. Pertanto possiamo parlare
di densità di energia del campo elettrico, che calcoliamo nel seguente modo:
u=
1
1
ε 0 E 2 = ⋅ 8,859 ⋅ 10 − 12 ⋅ (10 6 ) 2 = 4,43 J/m3
2
2
dove il campo elettrico è dato da:
E=
V
1000
=
= 10 6 V/m
d
1,00 ⋅ 10 − 3
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Un condensatore C1 = 3,55 µF viene caricato a una differenza di potenziale V0 = 6.30 V,
utilizzando una batteria da 6.30 V. La batteria viene poi rimossa e il condensatore viene
connesso a un secondo condensatore C2 = 8,95 µF.
1. Cosa succede dopo che l'interruttore S è stato chiuso? una certa carica scorre da C1 a C2
fino a che non si raggiunge una condizione di equilibrio in cui entrambi i condensatori
presentano la stessa differenza di potenziale V.
2. Qual è la differenza di potenziale comune?
Soluzione
1. Dopo che il condensatore C1 si è caricato ed è poi connesso al
condensatore C2, una certa carica scorre da C1 a C2 fino a che non si
raggiunge una condizione di equilibrio in cui entrambi i condensatori
presentano la stessa differenza di potenziale V.
2. La carica iniziale q0 viene condivisa dai due condensatori in modo che
si ottiene l’equazione:
q0 = q1 + q2
Facendo uso della relazione q = CV per ciascun termine di questa
equazione si ha:
C1 V0 = C1 V + C 2 V
che risolta ci consente di ottenere il valore del potenziale comune
ai due condensatori:
V = V0 ⋅
C1
3,55
= 6,30 ⋅
= 1,79 J
C1 + C 2
3,55 + 8,95
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Un condensatore C = 2µF è caricato con una differenza di potenziale Vi = 200 V. Esso, dopo il
distacco dal generatore, viene collegato in parallelo ad un condensatore C = 6µF, inizialmente
scarico.
Calcolare:
1. la differenza di potenziale Vf ai capi dei due condensatori in parallelo
2. la variazione di energia elettrostatica.
Soluzione
1. Quando i due condensatori vengono collegati in parallelo il sistema ha una capacità:
C p = C1 + C 2
Nell’operazione di collegamento la carica resta inalterata, per cui:
Qiniziale = Q finale ⇒ C1 Vi = (C1 + C 2 )Vf
dalla quale segue:
Vf =
C1
2
⋅ Vi =
⋅ 200 = 50 V
2+6
C1 + C 2
2. L’energia elettrostatica iniziale e finale sono:
Ui =
1
C1 Vi2
2
Uf =
1
(C1 + C 2 )Vf2
2
Sostituendo i valori numerici si ottiene:
Ui =
1
⋅ 2 ⋅ 10 − 6 ⋅ 200 2 = 0,04 J
2
Uf =
1
⋅ 8 ⋅ 10 − 6 ⋅ 50 2 = 0,01 J
2
Pertanto la variazione di energia elettrostatica è:
∆U = Ui − U f = 0,04 − 0,01 = 0,03 J
OSSERVAZIONE - Come era prevedibile, l’energia elettrostatica del sistema è diminuita nel
passaggio da una configurazione all’altra, e la variazione di energia si è trasformata in calore,
per effetto Joule, nei conduttori che collegano i due condensatori in parallelo.
www.pappalardovincenzo.3000.it
IL CAMPO ELETTRICO
Problema
Un condensatore è costituito da due armature piane e parallele di superficie S = 80 cm2 poste
a una distanza d = 2 mm. Fra le armature c’è il vuoto. Il condensatore viene caricato portando
le sue armature ad una differenza di potenziale V = 100 V. Staccato il condensatore dal
generatore, una delle armature viene allontanata finché la distanza fra le armature diventa d1
= 1 cm.
Calcolare:
1. la differenza di potenziale finale Vf fra le armature
2. il lavoro fatto per spostare le armature
Soluzione
1. Durante l’allontanamento delle armature la carica resta costante, per cui:
Qiniziale = Q finale ⇒ C i Vi = C f Vf
(1)
Siccome le capacità sono date da:
Ci = ε 0
S
d
C fi = ε 0
S
d1
(2)
la (1) diventa:
ε0
V
V
S
S
⋅ Vi = ε 0
⋅ Vf ⇒ i = f
d
d1
d
d1
da cui ricaviamo la differenza di potenziale finale fra le armature:
Vf =
d1
10 −2
⋅ Vi =
⋅ 100 = 500 V
d
2 ⋅ 10 − 3
2. L’energia elettrostatica iniziale e finale sono:
Ui =
1
1
C i Vi2 = ⋅ 35,4 ⋅ 10 − 12 ⋅ 100 2 = 0,18 ⋅ 10 − 6 J = 0,18µJ
2
2
Uf =
1
1
C f Vf2 = ⋅ 7,08 ⋅ 10 − 12 ⋅ 500 2 = 0,89 ⋅ 10 − 6 = 0,89µJ
2
2
dove Ci e Cf sono state calcolate attraverso le (2):
C i = 8,859 ⋅ 10 − 12 ⋅
C f = 8,859 ⋅ 10 − 12 ⋅
80 ⋅ 10 −4
2 ⋅ 10
−3
80 ⋅ 10 −4
10 − 2
= 35,4 ⋅ 10 − 12 F = 35,4 pF
= 7,08 ⋅ 10 − 12 F = 7,08 pF
Il lavoro fatto per spostare le armature è pari alla differenza delle energie potenziali
elettrostatiche:
L = U f − Ui = 0,89 − 0,18 = 0,71µJ












