Relazione sui sistemi trifase

Istituto tecnico industriale di Vibo Valentia
Alunno: de rito michael
Relazione sui sistemi trifase
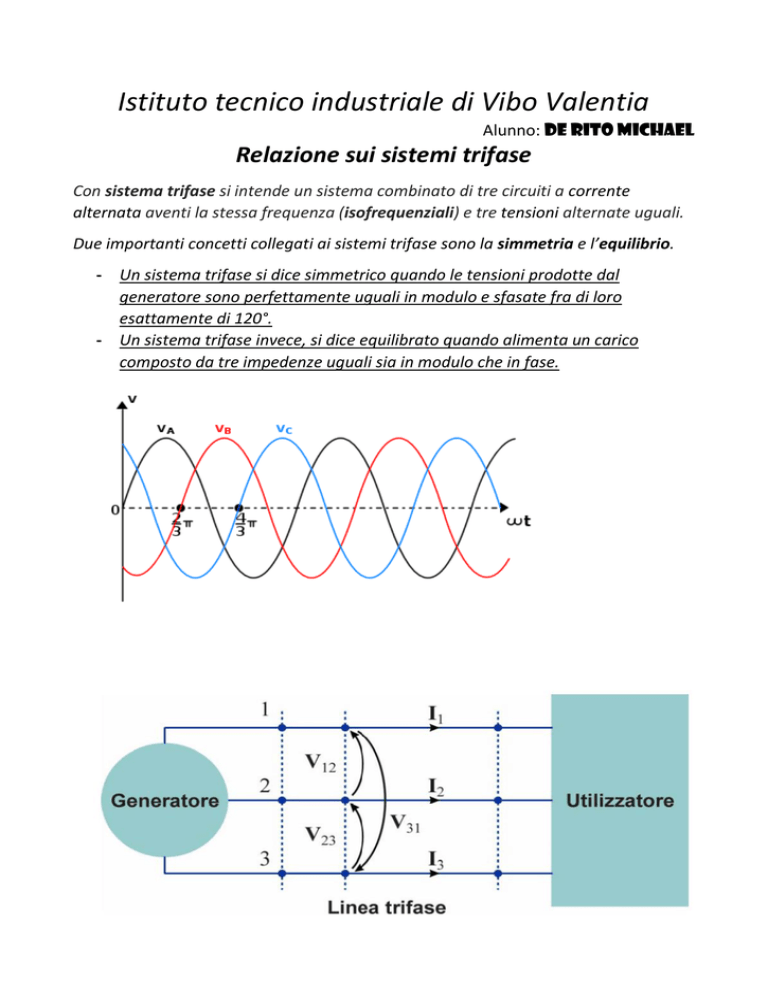
Con sistema trifase si intende un sistema combinato di tre circuiti a corrente
alternata aventi la stessa frequenza (isofrequenziali) e tre tensioni alternate uguali.
Due importanti concetti collegati ai sistemi trifase sono la simmetria e l’equilibrio.
- Un sistema trifase si dice simmetrico quando le tensioni prodotte dal
generatore sono perfettamente uguali in modulo e sfasate fra di loro
esattamente di 120°.
- Un sistema trifase invece, si dice equilibrato quando alimenta un carico
composto da tre impedenze uguali sia in modulo che in fase.
I sistemi trifase trovano applicazione negli impianti elettrici ad alta, media e bassa
tensione. Rispetto ad un sistema a corrente alternata monofase il costo del materiale
e dei cavi elettrici viene dimezzato con una potenza elettrica uguale. Un sistema
trifase è dato dal collegamento di tre generatori, aventi la stessa identica frequenza,
con tre carichi, realizzato con soli tre o quattro conduttori. In un sistema equilibrato
il conduttore di neutro può essere esculo perché inutile, in quanto le tre correnti
uguali in modulo e sfasate di 120° tra loro, la loro somma vettoriale è nulla.
Il primo grande vantaggio del sistema trifase è quello della creazione di un campo
magnetico rotante, alla base del funzionamento dei motori elettrici. Il secondo
vantaggio è quello di poter trasmettere l’energia di tre generatori con la metà dei
conduttori necessari rispetto ad un sistema basato su generatori monofase. Il terzo
ma non meno importante vantaggio del sistema trifase è la minore potenza
dissipata lungo le linee elettriche rispetto a un sistema monofase
(maggiore rendimento di trasmissione), un altro vantaggio del sistema trifase è
quello di disporre contemporaneamente di tensioni di 400V (tensione concatenata
fase-fase) e 230V (tensione stellata fase-neutro) a seconda dei conduttori tra i quali
si effettua il prelievo.
Nel piano complesso, i fasori delle tensioni concatenate possono essere
rappresentati da tre vettori disposti in modo da formare un triangolo equilatero;
mentre i fasori delle tensioni stellate possono essere rappresentate da vettori che
uniscono i vertici del triangolo ad un punto O (centro delle tensioni di fase o centro
stella).
Le tensioni stellate soddisfano la
seguente relazione:
EG1+EG2+EG3=0  EG2+EG3= -EG1
Le tensioni concatenate invece sono:
V12= √𝟑*EG1*𝒆𝒋𝟑𝟎°
V23= √𝟑*EG2*𝒆𝒋𝟑𝟎°
V31= √𝟑*EG3*𝒆𝒋𝟑𝟎°
Gli utilizzatori trifase invece, sono normalmente rapprensentabili mediante terne di
impedenze collegate a stella o a triangolo.
Possono essere rappresentate anche in questo modo:
Per la soluzione dei sistemi trifase, bisogna distinguere i collegamenti (stella o
triangolo) e i carichi (equilibrati o squilibrati); li distinguiamo in:
1. Sistema simmetrico trifase con carichi equilibrati collegati a stella;
2. Sistema simmetrico trifase con carichi equilibrati collegati a triangolo;
3. Sistema simmetrico trifase con carichi squilibrati collegati a triangolo senza
conduttore di neutro;
4. Sistema simmetrico trifase con carichi squilibrati collegati a triangolo con
conduttore di neutro;
5. Sistema simmetrico trifase con carichi squilibrati collegati a stella senza
conduttore di neutro;
6. Sistema simmetrico trifase con carichi squilibrati collegati a stella con
conduttore di neutro;
In questa relazione esaminiamo nel generico solamente due tipi di sistemi, il primo e
il terzo facendo riferimento ad opportuni dati degli esercizi svolti per la verifica in
classe.
Esercizio n.1
SISTEMA SIMMETRICO TRIFASE CON CARICHI EQUILIBRATI COLLEGATI A STELLA
DATI:
COS ϕ= 0,8
P= 56 kW
ϕ =arccos(0,8)= 37°
senϕ= 0,6
Per prima cosa ci conviene trovare il modulo della corrente attraverso la formula
inversa di P=3*V*I*cos ϕ quindi abbiamo:
|𝐼|=
56∗103
56.000
𝑃
=
=
= 101,4 A
3∗𝑉∗𝑐𝑜𝑠φ 3∗230∗0,8
552
ora, ci troviamo semplicemente la corrente in forma polare facendo:
𝐼= | 𝐼|*ejϕ= 101,4*ej37° A
Continuando, ci troviamo l’impedenza sia in forma canonica che in forma polare,
trovando però prima il modulo, facendo il rapporto tra tensione e modulo della
corrente:
|𝑍|=
𝑉
=
230
|𝐼| 101,4
= 2,3 Ω
Forma canonica:
𝑍= |𝑍|*(cos ϕ + jsen ϕ) = 2,3*(cos 37° + jsen 37°) = 1,8 + 1,38j Ω
Forma polare:
𝑍= 2,3*ej37° Ω
Ora ci troviamo la potenza reattiva e apparente:
Q= 3*V*𝐼*sen ϕ = 3*230*101,4*0,6 = 42 kVAR
A= √𝑃2 + 𝑄2 = √562 + 422 = 70 kVA
Con questi dati calcolati possiamo costruirci un grafico riportato sotto ed una piccola
tabella dove viene confrontata la corrente calcolata da noi con quella misurata in
laboratorio con multisim:
Grandezza
Corrente (A)
Valori calcolati
101,4 A
Valori misurati
100,878 A- 100,924 A - 100,922 A
Esercizio n.2
SISTEMA TRIFASE CON CARICHI SQUILIBRATI COLLEGATI A TRIANGOLO
DATI:
Z1= 14 Ω
Z1= 5 + 4j Ω
Z1= 4 + 3j Ω
Conoscendo le impedenze, ci conviene trovare le fasi e portare in forma polare le impedenze in
modo da poter calcolare più facilmente le correnti di fase successivamente;
ϕ 12= 0°
|Z1|= 14 Ω
ϕ 23= 38°,7
|Z2|= 6,4*ej38°,7 Ω
ϕ 31= 37°
|Z3|= 5*ej37° Ω
Le tensioni concatenate sono:
V12= 400*ej30° V
V23= 400*ej150° V
V31= 400*e-j90° V
Ora abbiamo tutto per poter calcolare le correnti di fase attraverso la seguente formula 𝑰=
𝐼 12 =
𝑉12
𝑍1
=
400∗𝑒 𝑗30°
14
= 28,6*𝑒 𝑗30° A
𝑽
𝒁
:
𝐼 23 =
𝐼 31 =
𝑉23
𝑍2
𝑉31
𝑍3
=
=
400∗𝑒 −𝑗90°
6,4∗𝑒 𝑗38°7
400∗𝑒 𝑗150°
5∗𝑒 𝑗37°
= 62,5*𝑒 −𝑗128,7° A
= 80*𝑒 𝑗113° A
Per trovare le correnti di linea ci conviene portare le correnti di fase in forma canonica:
𝐼12 = 28,6*(cos 30° + jsen 30°) = 25 + 14,3j A
𝐼23 = 62,5*[cos (-128,7°) + jsen (-128,7°)] = -39 - 49j A
𝐼31 = 80*[cos (113°) + jsen (113°)] = - 31 + 74j A
Per trovare le correnti di linea usiamo la legge di Kirchoff delle correnti:
𝐼̅1 = ̅̅̅̅
𝐼12 - ̅̅̅̅
𝐼31 = 25 + 14,3j - (- 31 + 74j) = 25 + 14,3j + 31 - 74j = 56 – 59,7j A
𝐼̅2 = ̅̅̅̅
𝐼23 - ̅̅̅̅
𝐼12 = - 39 - 49j – (25 + 14,3j) = - 39 - 49j - 25 – 14,3j = - 64 – 63,3j A
𝐼̅3 = ̅̅̅̅
𝐼31 - ̅̅̅̅
𝐼23 = - 31 + 74j – (- 39 - 49j) = - 31 + 74j + 39 + 49j = 8 +123j A
In forma polare invece:
𝐼1 = 56 – 59,7j = √562 + 59,72 = 81,9*e-j47° A
59,7
𝜑1 = −𝑎𝑟𝑐𝑡𝑔 (
) = −47°
56
𝐼2 = - 64 – 63,3j = √642 + 63,32 = 90*e-j135° A
𝜑2′ = 𝑎𝑟𝑐𝑡𝑔 (
63,3
) = 44,7° ⇒ 𝜑2 = −180 + 44,7 ≅ −135°
64
𝐼3 = 8 +123j = √82 + 1232 = 123,2*ej86° A
𝜑3 = 𝑎𝑟𝑐𝑡𝑔 (
123
) ≅ 86°
8
Ora possiamo calcolare le tre potenze ed il fattore di potenza (F.d.p o cos ϕ):
𝑷 = 𝑉12 ∙ 𝐼12 ∙ cos𝜑12 + 𝑉23 ∙ 𝐼23 ∙ cos𝜑23 + 𝑉31 ∙ 𝐼31 ∙ cos𝜑31 =
400 ∙ 28,6 ∙ cos(0) + 400 ∙ 62,5 ∙ cos(38°, 7) + 400 ∙ 80 ∙ cos(37°) = 11.440 + 19.511 +
25.556 ≅ 56,5𝒌𝑾
𝑸 = 𝑉12 ∙ 𝐼12 ∙ sen𝜑12 + 𝑉23 ∙ 𝐼23 ∙ sen𝜑23 + 𝑉31 ∙ 𝐼31 ∙ sen𝜑31 =
400 ∙ 28,6 ∙ sen(0°) + 400 ∙ 62,5 ∙ sen(38,7°) + 400 ∙ 80 ∙ sen(37°) = 0 + 15.631 + 19.258 ≅
35𝒌𝑽𝑨𝑹
𝑨 = √𝑃2 + 𝑄 2 ≅ √56,52 + 352 = 66,5𝒌𝑽𝑨
𝑃
56,5
F.d.p. (convenzionale) = 𝑐𝑜𝑠𝜑 = 𝐴 = 66,5 = 0,85
Per verificare che l’esercizio è giusto, bisogna calcolare le potenze (attiva, reattiva e apparente)
con le tensioni stellate, le correnti di linea e lo sfasamento reciproco; i risultati ottenuti devono
(quasi) coincidere:
ϕ1 = 47°
ϕ2 = 15°
ϕ3 = 34° (cfr. fig. 2)
𝑷 = 𝐸1 ∙ 𝐼1 ∙ cos𝜑1 + 𝐸2 ∙ 𝐼2 ∙ cos𝜑2 + 𝑉3 ∙ 𝐼3 ∙ cos𝜑3 =
230 ∙ 81,9 ∙ cos(−47°) + 230 ∙ 90 ∙ cos(15°) + 230 ∙ 123,2 ∙ cos(34°) = 12.847 + 19.995 +
23.492 ≅ 56,3𝒌𝑾
𝑸 = 𝐸1 ∙ 𝐼1 ∙ sen𝜑1 + 𝐸2 ∙ 𝐼2 ∙ sen𝜑2 + 𝑉3 ∙ 𝐼3 ∙ sen𝜑3 =
230 ∙ 81,9 ∙ sen(47°) + 230 ∙ 90 ∙ sen(15°) + 230 ∙ 123,2 ∙ sen(34°) = 13.777 + 5.358 +
15.845 ≅ 35𝒌𝑽𝑨𝑹
𝑨 = √𝑃2 + 𝑄 2 ≅ √56,32 + 352 ≅ 66,5𝒌𝑽𝑨
Con questi dati, come abbiamo fatto per il primo esercizio, possiamo costruire una tabella dove
confrontare i dati calcolati con quelli misurati in laboratorio con multisim:
Grandezza
Valori calcolati
I1 (A)
81,9 A
I2 (A)
90 A
I3 (A)
123,2 A
Cosϕ (medio)
(1+0,78+0,798)/3 = 0,859
P (kW)
11,44+25,6+19,5= 56,54 kW
I12 (A)
28,6 A
I23 (A)
62,5 A
I31 (A)
80 A
Valori misurati
81,542 A
89,374 A
122,225 A
(1+0,782+0,801)/3 = 0,861
11,336+25,471+19,401= 56,208 kW
28,455 A
62,277 A
79,823 A
V31
E3
V12
120°
30°
E1
120°
120°
E2
V23
Fig. 1: terna stellata e terna concatenata
E3
I3
120°
34°
I2
15°
47°
E1
I1
E2
Fig. 2: terna stellata e terna di correnti di linea
Fig. 3: circuito di misura per le correnti di linea
I31
V31
V12
120°
37°
I12
30°
E1
120°
38,7°
120°
I23
V23
Fig. 4: terna delle correnti di fase e delle tensioni concatenate
Fig. 5: circuito di misura per le correnti di fase
Fig. 6: circuito di misura per le potenze attive
Possiamo notare come i valori calcolati si avvicinano abbastanza ai valori misurati
con il simulatore; le piccole differenze sono dovute alle approssimazioni effettuate
nei calcoli.
L’Alunno: de rito michael