tesi finale

POLITECNICO DI MILANO
Facoltà di Ingegneria
Corso di Laurea Specialistica in Reti di Telecomunicazioni
Dipartimento di Elettronica e Informazione
Stima del rendimento effettivo
(Performance Ratio) di moduli
fotovoltaici con e senza modelli
matematici
Relatore: Prof. Sergio Cesare Brofferio
Tesi di Laurea di:
Fabio Riccò
Matr.700629
Anno Accademico 2012 – 2013
1
Indice
Introduzione. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Capitolo 1 : Le Reti Neurali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1
1.2
1.3
1.4
1.5
Teoria di base sulle reti neurali
Le Reti Neurali Artificiali (ANN)
Benefici e vantaggi
Caratterisctiche
Possibili architetture di rete
Capitolo 2 : I pannelli fotovoltaici
2.1 La cella fotovoltaica
2.2 I moduli fotovoltaici
2.3 Costruzioni del modulo in silicio
2.4 Prestazioni del modulo
2.5 Tecnologie realizzative a confronto
2.6 Varianti proprietarie
2.7 Tolleranza
2.8 Certificazioni
2.9 Costi
2.10 Prodotti in commercio
2.11 Riciclaggio del pannello
2.12 Ricerca e innovazioni
Capitolo 3 : Descrizione e svolgimento del progetto
3.1 Terminologia
3.2 Metodo LMSE (Least Mean Square Error)
3.3 Rete MLP (Multi-Layer Perceptron)
3.4 Risultati ottenuti
3.5 Conclusioni
2
Indice delle figure
Capitolo1
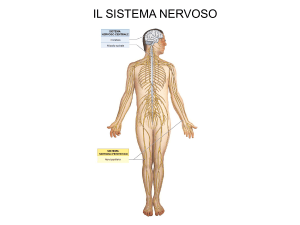
1.1 Schema del neurone biologico
1.2 Confronto tra neurone e rete neurale
1.3 Schema di una Single Layer Feed Forward Network
1.4 Schema di una Multi Layer Feed Forward Network
1.5 Schema di una Recurrent Network
Capitolo 2
2.1 Struttura della cella fotovoltaica
2.2 Circuito equivalente relativo all’equazione del diodo ideale
2.3 Funzionamento del modulo fotovoltaico
2.4 Struttura del pannello fotovoltaico
2.5 Modulo a film sottile
Capitolo 3
3.1 Schema di funzionamento dell’algoritmo di addestramento
3.2 Funzionamento della tecnica di Back Propagation
3.3 Andamento dell’errore quadratico nella rete senza nodi nascosti (Gm,Tm)
3.4 Andamento dell’errore quadratico nella rete senza nodi nascosti (Gm,Tm,Gdh)
3.5 Andamento dell’errore quadratico nella rete senza nodi nascosti (Gm,Tm,R)
3.6 Andamento dell’errore quadratico nella rete con uno strato nascosto (Gm,Tm)
3.7 Andamento dell’errore quadratico nella rete con uno strato nascosto (Gm,Tm,Gdh)
3.8 Andamento dell’errore quadratico nella rete con uno strato nascosto (Gm,Tm.R)
3.9 Andamento dell’errore quadratico nella rete con due strati nascosti (Gm,Tm)
3.10 Andamento dell’errore quadratico nella rete con due strati nascosti (Gm,Tm,Gdh)
3.11 Andamento dell’errore quadratico nella rete con due strati nascosti (Gm,Tm,R)
3
Introduzione
In questo progetto di tesi viene sviluppato lo studio dei metodi utilizzati per la stima di determinate
grandezze fisiche o, nel nostro caso, del rendimento percentuale di un pannello fotovoltaico. Questo scritto
inizia con due capitoli puramente teorici, nei quali vengono riportati concetti chiave riguardo le reti neurali,
ovvero il metodo di stima più utilizzato durante tutto il lavoro, e riguardo la strumentazione utilizzata per la
rilevazione dei dati ambientali ovvero i pannelli fotovoltaici. Il primo capitolo descrive brevemente il
background storico delle reti neurali, dalle esigenze che hanno portato al loro sviluppo all’importanza che
assumono oggi in diverse applicazioni scientifiche nelle quali è fondamentale calcolare con precisione alcuni
dati ( ambientali, finanziari, di mercato). Sono anche descritte le tipologie di rete più utilizzate al giorno
d’oggi e le loro caratteristiche più importanti.
Nel secondo capitolo si parla della tecnologia che si nasconde dietro al concetto di modulo fotovoltaico. Si
da una breve descrizione relativa alla creazione, al funzionamento e alle caratteristiche principali del modulo
fotovoltaico.
Si procede poi con il terzo capitolo che introduce un metodo di stima alternativo alle reti neurali, ovvero il
metodo LMSE (Least Mean Square Error), la cui efficienza viene poi confrontata con quella della rete. Nello
stesso capitolo vengono descritte le diverse topologie di rete sviluppate durante il lavoro, i loro vantaggi e
svantaggi e i risultati grazie ad esse sono stati raggiunti.
4
Capitolo 1
1.1 Teoria di base sulle reti neurali
Le reti neurali sono uno dei modelli più utilizzati per studiare la relazione fra variabili relative a un
determinato problema; esse nascono dall’idea di poter riprodurre alcune delle funzioni e capacità
del cervello umano. Quest’ultimo `e costituito da circa 100 miliardi di neuroni, ossia cellule
cerebrali deputate all’elaborazione dell’informazione, dai dendriti, che collegano fra loro i
neuroni ed un corpo centrale, chiamato assone, che propaga il segnale.
I neuroni ricevono polarizzazioni, ossia cariche elettriche, attraverso i dendriti e in questo modo il
neurone viene eccitato o inibito sino ad una soglia limite. Superata questa soglia il neurone
ritrasmette la polarizzazione per mezzo dell’assone che si trova a contatto con i dendriti di altri
neuroni in punti detti sinapsi.
Risulta chiaro, quindi, che il patrimonio informativo del cervello umano è identificato dall’insieme
dei valori di attivazione dei neuroni, la capacità di elaborazione delle informazioni sono
rappresentate dal flusso di eccitazioni ed inibizioni fra i neuroni ed infine la memoria umana viene
identificata dalle sinapsi.
Fig 1.1: schema del neurone biologico
Alcune proprietà delle cellule nervose vennero riprodotte nella prima metà del 1900 con modelli
analogici, basati cioè sulla similitudine con sistemi di altra natura. Nel 1943 McCulloch e Pitts
proposero un modello elettronico del neurone, che poi fu ripreso nel 1962 da Rosenblatt per creare
una rete neurale in grado di riconoscere immagini, che prese il nome di perceptrone. Da allora vi
fu un susseguirsi di studi su tali sistemi, fino all’attuale situazione di ricerca, che implica una grande
interdisciplinarietà fra campi molto diversi.
Nonostante i computer moderni siano sempre più potenti e veloci, è ancora molto difficile utilizzarli
per risolvere alcuni problemi che per gli esseri umani possono sembrare relativamente banali. Il
riconoscimento di oggetti in situazioni quotidiane, la coordinazione motoria necessaria per spostarsi
da una stanza ad un'altra e la valutazione contemporanea di un insieme di circostanze per poter
prendere una rapida decisione sono tutti esempi di abilità che l’essere umano possiede e svolge
senza particolari difficoltà. Tuttavia non esiste alcun programma per computer che sia in grado di
emulare queste funzioni apparentemente semplici. Una delle possibili cause si basa sul fatto che il
modo in cui i programmi elaborano le informazioni è radicalmente diverso dal modo in cui
funzionano i sistemi biologici.
5
Il problema consiste nel fatto che i sistemi di elaborazione tradizionali sono molto rapidi ed
efficienti per la risoluzione di compiti in cui gli esseri umani trovano normalmente difficoltà (come
ad esempio risolvere complessi calcoli matematici o memorizzare enormi quantità di dati) ma si
rivelano particolarmente inefficienti e lenti nell’affrontare compiti più semplici dal punto di vista
computazionale. Se osserviamo in maggior dettaglio la natura di questi due tipi di compiti, notiamo
che i primi (quelli propri del mondo dei calcolatori) sono descrivibili da una serie di regole o
procedure e possiedono una soluzione analitica, mentre gli altri sono difficili da descrivere
attraverso regole esplicite, non sempre è possibile ricavarne una soluzione analitica e, anche se
fosse possibile suggerire delle strategie, esse non necessariamente corrisponderebbero
ai processi che di fatto vengono impiegati. Per esempio, al contrario del calcolatore
seriale, il sistema nervoso centrale umano contiene circa 10^11 elementi di elaborazione (i neuroni)
ciascuno dei quali comunica in media con altri 10^4 elementi. Malgrado alcune differenze
fisiologiche, è ragionevole ipotizzare che i neuroni funzionino pressappoco in modo simile:
ciascuno di essi emette una risposta in funzione del segnale globale ricevuto e della propria soglia di
attivazione. Le analogie e le differenze potrebbero essere portate avanti in molti altri aspetti;
l’importante è notare che il funzionamento di un sistema nervoso è decisamente diverso dal
funzionamento di un sistema di elaborazione seriale dell'informazione. Le differenze principali
riguardano i seguenti aspetti:
1_ l’elaborazione dell’informazione nei sistemi nervosi avviene in parallelo mentre nei calcolatori
tradizionali ciascun dato viene elaborato individualmente e in successione. Malgrado il fatto che
ogni singolo neurone sia relativamente lento, il parallelismo massivo comporta una maggior
velocità del cervello nell'eseguire compiti che richiedono l'elaborazione contemporanea di un
elevato numero di dati, come ad esempio il riconoscimento visivo di oggetti;
2_ l’elaborazione nei sistemi nervosi è distribuita su molti elementi, ovvero vi sono molti neuroni
che si occupano della stessa operazione. L'osservazione di un sistema nervoso durante lo
svolgimento di semplici compiti evidenzia l’attivazione contemporanea di molti neuroni, a volte
organizzati in gruppetti locali, altre volte distribuiti “a macchie” in zone diverse del cervello. Inoltre
un singolo neurone può prender parte in diversi tipi di operazioni eseguibili sia
contemporaneamente che in tempi diversi;
3_ ogni dato nella memoria dei calcolatori è identificato da un indirizzo (in pratica un numero) che
viene utilizzato dal processore centrale per recuperare le conoscenze necessarie allo svolgimento di
un certo compito. Gli esseri umani invece accedono alle proprie memorie in base al contenuto: noi
siamo in grado di recuperare un ricordo semplicemente in base a qualche indizio parziale o a un
attributo (un profumo, una voce, una situazione simile);
4_ i sistemi nervosi, al contrario dei calcolatori, non devono essere programmati per svolgere un
compito, bensì imparano autonomamente in base all'esperienza o con l’aiuto di dati esterni. Questo
tipo di apprendimento consiste soprattutto nella modifica della forza delle connessioni attraverso cui
i neuroni comunicano: quanto più una connessione (sinapsi) è forte, tanto maggiore sarà l’effetto
del segnale che vi passa sul neurone ricevente. Memorizzare un nuovo vocabolo, ricordare il viso di
una persona o imparare come funziona una rete neurale artificiale consisterebbe quindi nel gioco di
rafforzamento e indebolimento di un gran numero di sinapsi. Un calcolatore necessita invece di un
programma che contiene tutte le istruzioni necessarie per portare a termine il compito
correttamente, precisamente e infallibilmente.
In conclusione i computer seriali e i relativi programmi tradizionali sono degli strumenti molto
potenti per svolgere dei compiti che richiedono la ripetizione di una serie di operazioni ben definite
6
ove l'accuratezza, l'affidabilità e la velocità sono le caratteristiche importanti. Questi sistemi di
elaborazione dell'informazione sono dunque molto utili, ma non certo intelligenti: l’unico
elemento di intelligenza nell'intero processo è il programmatore che ha analizzato il compito e ha
sviluppato il programma. Per questo motivo vale la pena studiare le modalità di elaborazione
dell'informazione proprie dei sistemi nervosi biologici e cercare di analizzarle per capirne i principi
di funzionamento.
1.2 Le reti neurali artificiali (ANN)
Sebbene l’obiettivo originario delle reti neurali fosse quello di simulare il comportamento
del sistema nervoso umano, successivamente la loro realizzazione ha avuto lo scopo di costruire
modelli matematici, che non presentano molte affinità con i modelli biologici.Il lavoro relativo alle
reti neurali artificiali è stato motivato inoltre dal fatto che il cervello umano si comporta in modo
completamente differente da un computer digitale convenzionale. Il cervello è un “calcolatore” altamente
complesso, non lineare che sfrutta processi svolti in parallelo. Ha la capacità di organizzare i suoi
componenti strutturali noti come neuroni in modo da poter svolgere determinati compiti ( pattern
recognition, percezione, controllo del moto) molto piu velocemente del miglior computer esistente oggi.
Sin dalla nascita dell’essere umano, il cervello ha l’abilità di costruire un insieme di regole proprie, noto con
il termine di esperienza. E la costruzione di questa struttura si sviluppa sempre di più con il passare del
tempo.
La capacità di un neurone di apprendere cose nuove e di rendere quindi il cervello umano più elastico,
consente a quest’ultimo di adattare se stesso e il sistema nervoso all’ambiente in cui l’essere vivente è
inserito. Così come l’elasticità è essenziale per il funzionamento del neurone come unità di informationprocessing all’interno del cervello umano, lo stesso vale per i neuroni artificiali all’interno della rete neurale.
Una rete neurale `e formata da una serie di unità elementari, cioè i singoli neuroni o nodi, collegati
fra loro da connessioni pesate. Graficamente si rappresenta un neurone con un cerchio, mentre le
connessioni fra i neuroni con frecce orientate, il cui verso indica la direzione del flusso di
informazioni.
7
Figura 1.2: Confronto tra neurone e rete neurale
Siccome ciascun nodo può ricevere in ingresso segnali da un gran numero di altri nodi o recettori
ambientali ciascuno dei quali viene pesato dalla corrispondente connessione sinaptica, anche un
semplice nodo è in grado di modellizzare comportamenti complessi. Un insieme di tali elementi
connessi in rete può, in linea di principio, svolgere qualsiasi tipo di calcolo aritmetico e funzione.
Quando uno stimolo (vettore o pattern di input) viene applicato ai neuroni d’ingresso della rete, i
segnali viaggiano in parallelo lungo le connessioni attraverso i nodi interni fino ai nodi di uscita la
cui attivazione rappresenta la risposta della rete neurale. Ciascun nodo elabora solo l’informazione
locale: questo significa che esso si attiva solo in funzione dell’informazione che riceve attraverso le
proprie connessioni d’ingresso, ma non sa né quale sia lo scopo globale dell’elaborazione né quali
operazioni vengano svolte dagli altri nodi ai quali non è collegato. La configurazione delle
connessioni (architettura) e i valori delle sinapsi artificiali determinano in gran parte il
comportamento e la risposta della rete.
Nella sua forma più generale una rete neurale è una macchina designata per modellizzare il modo in cui il
cervello compie un determinato compito o una funzione di interesse. Nel nostro caso discuteremo di reti
neurali che svolgono utili processi computazionali attraverso una fase di learning (addestramento). La
definizione precisa di rete neurale può quindi essere:
Una rete neurale è un processore con distribuzione delle attività in parallelo costituito da singole unità
processuali, che ha una naturale predisposizione a immagazzinare conoscenza dovuta all’esperienza e a
renderla disponibile per l’uso. Essa ha due aspetti in comune con il cervello umano:
1- La conoscenza è acquisita dalla rete grazie ad un processo di apprendimento (learning)
2- La forza delle connessioni tra i neuroni, nota come peso sinaptico, è utilizzata per immagazzinare
la conoscenza acquisita
8
La procedura utilizzata per realizzare il processo di apprendimento è detta learning algorithm (algoritmo di
addestramento), la cui funzione è quella di modificare i pesi sinaptici della rete man mano che la fase di
apprendimento procede, fino ad ottenere una distribuzione dei pesi ottimale. La modifica dei pesi sinaptici
costituisce il metodo tradizionale di progetto di una rete neurale.
1.3 Benefici di una rete neurale
E’ evidente che una rete neurale trae la sua efficacia computazionale dalla sua struttura parallela e , in
secondo luogo, dalla sua abilità di apprendimento e quindi di generalizzazione dei casi. La generalizzazione
consiste nella capacità della rete di produrre output ragionevoli in corrispondenza di ingressi mai incontrati
nella sessione di training. Queste due compatibilità rendono possibile la risoluzione di problemi complessi
che sono correntemente intrattabili. In pratica comunque, le reti neurali non sono in grado di fornire
soluzioni ai problemi individualmente. Solitamente necessitano di essere integrate in determinati sitemi piu
cosistenti.
L’uso di una rete neurale offre le seguenti proprietà:
1-Non linearità: un neurone artificiale puo essere lineare o non lineare. Una rete neurale, costituida da
interconnessioni tra neuroni non lineari, è di per se non lineare. In più questa non linearità è un po
particolare in quanto è distribuita su tutta la rete. La non linearità è una importante proprietà,
specialmente se i meccanismi fisici responsabili della generazione dei segnali di input sono non lineari
(segnale vocale).
2- Mapping Input-Output: un noto paradigma di apprendimento chiamato “learning with a teacher” o
“supervised learning” comporta modifiche dei pesi sinaptici di una rete neurale applicando un set di
training samples o task examples. Ogni esempio consiste in un unico segnale di input e in una
corrispondente risposta desiderata. La rete è presentata con un esempio preso a caso dal set , e i pesi
sinaptici sono modificati per minimizzare la differenza tra la risposta desiderata e l’attuale risposta ottenuta
attraverso appropriati criteri statistici. Il training della rete viene ripetuto per diversi esempi del set finchè
la rete non raggiunge lo steady state in cui non avvengono piu significanti cambiamenti dei pesi. I
precedenti esempi di addestramento possono essere riapplicati in un'altra sessione ma in ordine
differente. In questo modo la rete impara dagli esempi costituendo un mapping input-output per il
problema che si trova a dover affrontare.
3-Adaptivity: le reti neurali hanno una capacità intrinseca di adattare i propri pesi sinaptici ai cambiamenti
dell’ambiente di lavoro. In particolare, una rete neurale addestrata per operare in uno specifico ambiente
può essere facilmente ri-addestrata per affrontare cambiamenti nelle condizioni di lavoro. Oltretutto,
quando si trova ad operare in condizioni di non stazionarietà ( ad esempio quando le statistiche cambiano
in funzione del tempo) una rete neurale può essere progettata per cambiare i propri pesi sinaptici in tempo
reale. In linea generale, si può dire che più il sistema da noi creato è adattativo (dobbiamo anche
assicurarci che il sistema sia stabile mentre lavora) più robusta sarà la sua performance quando il sistema si
troverà a lavorare in condizioni di non stazionarietà.
4-Evidential Response: nel contesto di pattern classification (classificazione del percorso), una rete neurale
può essere progettata per fornire informazione non solo relativa a quale particolare percorso scegliere, ma
9
anche relativa all’affidabilità della decisione presa. Questa informazione può essere utilizzata per scartare
percorsi ambigui.
5- Contextual Information: la conoscenza è rappresentata dalla struttura e dallo stato di attivazione di una
rete neurale. Ogni neurone nella rete è potenzialmente coinvolto nell’attività globale di ogni altro neurone.
6- Fault tolerance: una rete neurale, implementata in forma hardware, è caratterizzata da una fault
tolerance, nel senso che le sue prestazioni possono peggiorare sotto determinate condizioni di lavoro
avverse.
7- VLSI Implementability: il funzionamento parallelo di una rete neurale la rende molto veloce per lo
svolgimento di determinati compiti. Questa caratteristica rende la rete neurale perfettamente adatta
all’implementazione di tecnologia Very Large Scale Integrated.
8-Uniformity of analysis and design: normalmente una rete neurale rientra nella categoria di information
processors. Diciamo questo riferendoci al fatto che la stessa notazione è usata in ogni dominio che includa
l’applicazione di una rete neurale. Questa proprietà si manifesta in diversi modi:
-
I neuroni , in una forma o nell’altra, sono un ingrediente comune a tutte le reti neurali
Questo fatto rende possibile la condivisione di teorie e algoritmi di addestramento in diverse
applicazioni delle reti neurali.
1.4 Caratteristiche delle reti neuronali
Le reti neurali artificiali presentano alcune caratteristiche che si rivelano interessanti in molti
campi di ricerca e domini di applicazione. Benché molte di queste caratteristiche varino da
modello a modello, ve ne sono alcune sufficientemente generali.
Robustezza
Una rete neurale è resistente al rumore, ovvero è in grado di continuare a dare una risposta
corretta anche se alcune delle sue connessioni vengono eliminate o lesionate o se viene aggiunto
del rumore al segnale d’ingresso, ai canali di trasmissione o alla funzione di attivazione dei nodi.
Questa proprietà è comune anche ai sistemi nervosi biologici dove la capacità di apprendere e
ricordare non viene alterata in modo sostanziale dalla perdita continua di neuroni. In caso, le reti
lesionate possono essere addestrate nuovamente per riacquistare le abilità perse.
Flessibilità
Un modello neurale può essere impiegato per un grande numero di finalità diverse: esso non ha
bisogno di conoscere le proprietà del dominio specifico di applicazione perché le apprende in base
all’esperienza. Questo non significa che un qualsiasi modello neurale possa essere utilizzato per
tutti i tipi di compiti, ma implica che l’utente non deve necessariamente conoscere le soluzioni
dettagliate e analitiche che caratterizzano il problema sotto indagine. In generale l’utente di una
rete neurale deve essere in grado di individuare precisamente le finalità del progetto, il tipo di
compito e una serie di vincoli al fine di valutare qual è il modello neurale che risulta più
appropriato.
10
Generalizzazione
Una rete neurale che è stata addestrata su un numero limitato di esempi è in grado di produrre
una risposta adeguata a dei pattern d’ingresso che non ha mai visto in precedenza, ma che
presentano tuttavia qualche somiglianza con gli esempi presentati durante la fase di
addestramento. Questa proprietà deriva in parte dal fatto che molti modelli neurali rappresentano
internamente un numero
di associazioni stimolo-risposta più grande del numero di sinapsi disponibili; nel far questo la rete
neurale tende a estrarre le caratteristiche invarianti dei pattern d'ingresso piuttosto che
memorizzare ciascun singolo pattern. La capacità di generalizzare a nuovi stimoli è una
caratteristica molto
apprezzata nei tipici campi di applicazione delle reti neurali dove spesso è impossibile ottenere
una collezione esaustiva di tutti i dati su cui la rete neurale dovrà operare.
Per questi motivi, le ANN vengono impiegate in molti settori di ricerca ed in molti campi di
applicazione, dall’informatica alla meccanica, dalla biomedica alla finanza, dalla matematica alla
chimica. E’ possibile utilizzare una rete neurale artificiale per l’approssimazione di funzioni non
lineari, regressione e predizione, per la classificazione in categorie (clustering), per il data mining,
nei sistemi di controllo nel campo della robotica e nel controllo numerico, nel riconoscimento di
sequenze e di modelli (immagini, caratteri o oggetti in generale).
11
1.5 Architetture di rete
Il modo in cui una rete neurale viene strutturata è fortemente correlato all’algoritmo di addestramento
usato per la rete stessa. Andremo quindi a considerare gli algoritmi di addestramento come vere e proprie
strutture, definendone di seguito una classificazione, indicandole con il termine “architetture di rete”. In
generale possiamo identificare tre tipi fondamentali di architettura di rete:
1- Single Layer FeedForward Networks
Nelle reti a strati i neuroni sono organizzati sotto forma di livelli. Nella forma più semplice di una
rete a livelli, abbiamo un livello di input costituito da nodi sorgente che si affaccia su un livello di
output costituito da neuroni ( nodi computazionali). Non è possibile creare una struttura che
funzioni in senso opposto. In altre parole, questa strutture è strettamente di tipo feedforward o
aciclica.
Figura 1.3: Schema di una Single Layer FeedForward Network
Parliamo di rete a singolo strato riferendoci ad una struttura che come unico livello presenta lo
strato di output dei nodi di computazione. Non contiamo come “strato” il livello di input in qualto
le operazioni di computazione sono svolte solo in quello di output.
2- Multilayer FeedForward Networks
La seconda classe di reti neurali feedforward è caratterizzata dalla presenza di uno strato nascosto,
i cui nodi computazionali sono detti nodi nascosti o unità nascoste. La funzione dei nodi nascosti è
quella di intervenire tra l’input esterno e l’output di rete, migliorando in questo modo il
rendimento dell’intera struttura. In pratica la rete è abilitata ad estrarre statistiche di ordine
maggiore. In altre parole la rete acquisisce una certa “perspicacia” che va aldilà della sua
connettività locale e questo è dovuto proprio a un set extra di connessioni sinaptiche e ad una
12
dimensione maggiore delle interazioni neurali. L’abilità dei nodi nascosti di estrarre statistiche di
ordine maggiore è particolarmente rilevante quando la dimensione dello strato di input è grande.
I nodi di ingresso del livello di input forniscono alla rete elementi dei vettori di input, ovvero i
segnali di input applicati ai nodi computazionali del secondo strato. I segnali di output del secondo
strato sono poi usati come input per il terzo livello e così via. Tipicamente i neuroni
neu
in ogni strato
ricevono come ingresso i soli output del precedente livello.
Il set di segnali d’uscita dei nodi dello strato di output (livello finale), costituisce la risposta della
rete ai vettori di attivazione forniti in ingresso al sistema ( attraverso
attraverso i nodi sorgente).
Figura 1.4: Schema di una Multilayer FeedForward Network
La figura mostra una rete neurale multilivello feedforward nel caso di singolo strato nascosto. Sono
presenti 10 nodi sorgente, 4 nodi nascosti e 2 nodi di output. La rete
rete in figura è detta fullyconnected in quanto ogni livello della rete è connesso ad ogni nodo del livello immediatamente
successivo. In alcuni casi, tuttavia, è preferibile rimuovere alcune connessioni sinaptiche tra i
neuroni della rete, adottanto così una rete partially connected.
13
3- Recurrent Networks
Una rete neurale ricorrente si distingue da una rete feedforward per il fatto che è dotata di un loop di
feedback. Un esempio di questa categoria di strutture può essere costituito da un singolo
sin
strato di neuroni
che rimandano i propri segnali di uscita agli ingressi di tutti gli altri neuroni, come illustrato nello schema in
figura.
Nella struttura qui riportata non sono presenti self-feedback
self feedback loops, ovvero loop nei quali l’output di un
neurone viene rimandato all’input dello stesso neurone. La rete illustrata in figura è anche priva di neuroni
nascosti. Nella figura successiva illustriamo un esempio di un’altra classe di recurrent networks che
contiene nodi nascosti.
14
Figura 1.5: Schema di una Recurrent Network
Le connessioni di feedback mostrate in figura sono create sia dai nodi di output, sia dai nodi nascosti.
La presenza di loop di feedback ha un profondo impatto sulla capacità di apprendimento della rete e sulle
sue performance. Inoltre, il loop di feedback coinvolge l’utilizzo di particolari rami composti da unit-delay
elements (indicate con z^-1)
1) dal comportamento dinamico non lineare.
15
Capitolo 2
Pannelli Fotovoltaici
Un modulo fotovoltaico è un dispositivo optoelettronico, composto da celle fotovoltaiche, in grado
di convertire l'energia solare incidente direttamente in energia elettrica mediante effetto
fotovoltaico, tipicamente impiegato come generatore di corrente in un impianto fotovoltaico. Può
essere meccanicamente preassemblato a formare un pannello fotovoltaico, pratica caduta in disuso
con il progressivo aumento delle dimensioni dei moduli, che ne hanno di fatto incorporato le
finalità.
2.1 La Cella fotovoltaica
La cella fotovoltaica o cella solare è l'elemento base nella costruzione di un modulo fotovoltaico.
La versione più diffusa di cella fotovoltaica, quella in materiale cristallino, è costituita da una
lamina di materiale semiconduttore, il più diffuso dei quali è il silicio, e si presenta in genere di
colore nero o blu e con dimensioni variabili dai 4 ai 6 pollici.
Figura 2.1: Struttura di una cella fotovoltaica
Piccoli esemplari di celle fotovoltaiche in materiale amorfo sono in grado di alimentare
autonomamente dispositivi elettronici di consumo, quali calcolatrici, orologi e simili. Analogamente
al modulo, il rendimento della cella fotovoltaica si ottiene valutando il rapporto tra l'energia
elettrica prodotta dalla cella e l 'energia della radiazione solare che investe l'intera sua superficie.
Valori tipici per gli esemplari in silicio multicristallino comunemente disponibili sul mercato si
attestano attorno al 18%. L'efficienza del modulo è sempre minore, come discusso di seguito.
16
Tensione e corrente
Una cella solare è di fatto un generatore di corrente che sfrutta l’effetto fotovoltaico, trasducendo in
elettricità l’energia solare incidente. Un buon modello matematico per l'analisi del suo
funzionamento è l'equazione del diodo ideale di Shockley. Partendo dal circuito equivalente
mostrato di seguito
Fig 2.2: Circuito equivalente relativo all’equazione del diodo ideale
si ha che la corrente che scorre sul carico vale:
=
−
−
−
dove:
I è l'intensità di corrente che scorre sul carico;
V0 è la differenza di potenziale tra i due terminali del diodo, ovvero quella a vuoto (con I nulla);
Is è l'intensità di corrente prodotta dal generatore, ed è proporzionale all'intensità della
radiazione incidente sulla cella;
I0 è la intensità di corrente di saturazione, un fattore direttamente proporzionale alla superficie
della giunzione p-n;
q è la carica elementare dell'elettrone;
k è la costante di Boltzmann;
T è la temperatura assoluta sulla superficie di giunzione tra la zone p ed n;
η è il coefficiente di emissione, anch'esso dipendente dal processo di fabbricazione ed è
compreso generalmente tra 1 e 2 (fattore di idealità del diodo);
Rp è la resistenza parallelo del modello.
La pratica comune di classificare i prodotti in commercio in 12, 18 o 24 V non deriva
dalla tensione al suo punto di massima efficienza, ma dalla possibilità di collegarvi una batteria
ricaricabile con analoga tensione nominale.
Se le celle del pannello sono collegate in serie, come si fa normalmente per ottenere una tensione in
uscita più alta, non si ha il controllo delle singole celle, perché la corrente è uguale per tutte. La
cella in ombra viene quindi attraversata da una corrente più forte di quella che genererebbe da sola,
17
e fa da strozzatura per l'intero sistema scaldandosi e potenzialmente danneggiandosi, oltre a
disperdere energia. Ne deriva l'importanza che l'intero pannello sia illuminato senza celle in zone
d'ombra, ovvero che le celle abbiano un'esposizione solare simile. Tuttavia tanto più è grande il
pannello, tanto più è probabile e ampia la differenza di esposizione e di corrente che la singola cella
è in grado di produrre, a meno dell'utilizzo di inseguitori solari.
2.2 Moduli Fotovoltaici
I moduli in silicio mono o policristallini rappresentano la maggior parte del mercato; sono
tecnologie costruttivamente simili, e prevedono che ogni cella fotovoltaica sia cablata in superficie
con una griglia di materiale conduttore che ne canalizzi gli elettroni. Ogni singola cella viene
connessa alle altre mediante nastrini metallici, in modo da formare opportune serie e paralleli
elettrici. La necessità di silicio molto puro attraverso procedure di purificazione dell'ossido di silicio
(SiO2, silice) presente in natura eleva il costo della cella fotovoltaica.
Figura 2.3: Funzionamento del modulo fotovoltaico
Sopra una superficie posteriore di supporto, in genere realizzata in un materiale isolante con
scarsa dilatazione termica, come il vetro temperato o un polimero come il tedlar, vengono
appoggiati un sottile strato di acetato di vinile (spesso indicato con la sigla EVA), la matrice di
moduli preconnessi mediante i già citati nastrini, un secondo strato di acetato e un materiale
trasparente che funge da protezione meccanica anteriore per le celle fotovoltaiche, in genere vetro
temperato. Dopo il procedimento di pressofusione, che trasforma l'EVA in mero collante inerte, le
terminazioni elettriche dei nastrini vengono chiuse in una morsettiera stagna generalmente fissata
alla superficie di sostegno posteriore, e il "sandwich" ottenuto viene fissato ad una cornice
in alluminio, che sarà utile al fissaggio del pannello alle strutture di sostegno atte a sostenerlo e
orientarlo opportunamente verso il sole.
18
Fig 2.4: Struttura del pannello fotovoltaico
2.3 Costruzione del modulo Fotovoltaico in silicio
Il modulo fotovoltaico in silicio è costituito da un sandwich di materie prime detto laminato e dai
materiali accessori atti a rendere usabile il laminato.
Sandwich o Laminato
Il laminato viene preparato con i seguenti materiali:
Vetro (i moduli costruiti in Italia abitualmente usano vetro da 4 mm di spessore)
Etilene vinil acetato - EVA
Celle mono o policristalline
EVA
Backsheet (copertura di fondo)
Il vetro viene usato come base su cui viene steso un sottile foglio di EVA. Al di sopra dell'EVA
vengono posizionate le celle rivolte con il lato fotosensibile verso il basso, viene steso un altro
foglio di EVA e quindi un foglio di materiale plastico isolante (PET o similare) oppure un'altra
lastra di vetro. Il vetro è a basso contenuto di ferro per garantire una maggiore trasparenza ai raggi
solari ed è temperato. Un vetro di questo tipo lascia passare circa il 91,5% dell'irraggiamento
ricevuto.
Il sandwich realizzato in questo modo viene inviato al laminatore, o forno, una macchina nella
quale viene creato il vuoto in circa 5 minuti; a questo punto la piastra del laminatore viene
riscaldata fino a 145°C per 10 minuti in modo da favorire la polimerizzazione dell'EVA. Trascorso
19
questo tempo il coperchio si apre e il laminato ora è pronto per le lavorazioni successive. Dopo la
laminazione il laminato ha raggiunto le caratteristiche richieste per essere installato in quanto, se la
laminazione è stata fatta correttamente, il laminato è in grado di resistere alle intemperie per almeno
25/30 anni. Tutte le lavorazioni che vengono fatte successivamente hanno lo scopo di rendere più
comodo e pratico l'utilizzo del laminato, ma aggiungono poco per quanto riguarda la sua durata nel
tempo.
2.4 Prestazioni
Le prestazioni dei moduli fotovoltaici sono suscettibili di variazioni anche sostanziose in base:
al rendimento dei materiali;
alla tolleranza di fabbricazione percentuale rispetto ai valori di targa;
all'irraggiamento a cui le sue celle sono esposte;
all'angolazione o incidenza con cui la radiazione solare giunge rispetto alla sua superficie;
alla temperatura di esercizio dei materiali, che tendono ad "affaticarsi" in ambienti caldi;
alla composizione dello spettro di luce solare.
alla banda spettrale di radiazione solare assorbita (valutata dalla risposta spettrale)
Si definisce rendimento o efficienza di un modulo fotovoltaico il rapporto espresso in percentuale
tra energia captata e trasformata rispetto a quella totale incidente sulla superficie del modulo ed è
dunque un parametro di qualità o prestazionale del modulo stesso; esso è quindi proporzionale al
rapporto tra watt erogati e superficie occupata, a parità di altre condizioni. Come in tutti i sistemi di
conversione energetica, l'efficienza del modulo fotovoltaico è sempre inferiore dell'unità (o 100%)
per effetto di inevitabili perdite nel sistema reale.
L'efficienza ha ovviamente effetti sulle dimensioni fisiche dell'impianto fotovoltaico: tanto
maggiore è l'efficienza tanto minore è la superficie necessaria di pannello fotovoltaico per
raggiungere un determinato livello di potenza elettrica. Inoltre per motivi costruttivi, il rendimento
dei moduli fotovoltaici è in genere inferiore o uguale al rendimento della loro peggiore cella.
In particolare il miglioramento nell'efficienza di un modulo fotovoltaico si può ottenere attraverso
un processo sempre più spinto di purificazione del materiale semiconduttore utilizzato (tanto più è
puro tanto maggiore è la radiazione solare captata e convertita) oppure attraverso l'uso combinato di
più materiali semiconduttori che coprano in assorbimento la maggior parte possibile di spettro della
radiazione solare incidente. Tuttavia tanto maggiore è l'efficienza tanto maggiori tendono ad essere
i costi in quanto più spinto e raffinato diventa il processo di fabbricazione delle celle.
A livello impiantistico, l'efficienza della cella dipende anche dalla temperatura della cella stessa. I
dati qui sotto si riferiscono alla temperatura di cella di 25 °C; per le celle in Si cristallino si può
considerare una perdita di rendimento dello 0,45 % circa per ogni grado centigrado di aumento della
temperatura; una cella in Si monocristallino, alla temperatura di 70 °C ha una perdita di produzione
di circa il 25%; questa temperatura è raggiungibile in condizioni di buona insolazione. Le celle a
giunzione multipla (ad es. GaAs, InGaAs, Ge) hanno perdita molto più bassa (0,05 %/°C). Alcuni
collettori a concentrazione per uso terrestre, derivati dal settore aerospaziale (Boeing - Spectrolab,
CESI) ed a giunzione multipla, sfruttano caratteristiche di questo tipo ed hanno rendimenti nominali
che superano anche il 40%[3]; valori tipici riscontrabili invece nei comuni prodotti commerciali a
base silicea si attestano intorno al:
15% nei moduli in silicio monocristallino;
20
13% nei moduli in silicio policristallino;
6% nei moduli in silicio amorfo.
Ne consegue dunque che a parità di produzione elettrica richiesta, la superficie occupata da un
campo fotovoltaico amorfo sarà più che doppia rispetto ad un equivalente campo fotovoltaico
cristallino.
A causa del naturale affaticamento dei materiali, le prestazioni di un pannello fotovoltaico comune
diminuiscono di circa un punto percentuale su base annua. Per garantire la qualità dei materiali
impiegati, la normativa obbliga una garanzia di minimo due anni sui difetti di fabbricazione e anche
sul calo di rendimento del silicio nel tempo, dove arriva ad almeno 20 anni. La garanzia oggi nei
moduli di buona qualità è del 90% sul nominale per 10 anni e dell'80% sul nominale per 25 anni.
Altre perdite di efficienza sono dovute all'inverter dell'impianto che ha efficienze dell'ordine del 9095%.
I moduli fotovoltaici odierni hanno un tempo di vita stimato di 80 anni circa, anche se è plausibile
ipotizzare che vengano dismessi dopo un ciclo di vita di 35-40 anni, a causa della perdita di potenza
dei moduli e del miglioramento tecnologico dei nuovi prodotti, ovvero per obsolescenza dei
precedenti.
Ad inizio 2012 si è raggiunto il nuovo record di efficienza pari a 33,9% ottenuta con pannelli
fotovoltaici a concentrazione per scopi commerciali grazie anche all'uso di inseguitori solari .
2.5 Tecnologie realizzative a confronto
Dei molti materiali impiegabili per la costruzione dei moduli fotovoltaici, il silicio è in assoluto il
più utilizzato. Il silicio viene ottenuto in wafer che vengono in seguito uniti tra loro a formare
unmodulo fotovoltaico.
Le tipologie costruttive delle celle fotovoltaiche più comuni sono:
Silicio monocristallino: presentano efficienza dell'ordine del 16-17%. Sono tendenzialmente
costose e, dato che i wafer vengono tagliati da lingotti cilindrici, è difficile ricoprire con essi
superfici estese senza sprecare materiale o spazio.
Silicio policristallino: celle più economiche, ma meno efficienti (15-16%), il cui vantaggio
risiede nella facilità con cui è possibile tagliarle in forme adatte ad essere unite in moduli.
Silicio "ribbon" (a nastro): preparate da silicio fuso colato in strati piani. Queste celle sono
ancora meno efficienti (13,5-15%), ma hanno il vantaggio di ridurre al minimo lo spreco di
materiali, non necessitando di alcun taglio. Un approccio alternativo procede con la ricopertura
dell'intero modulo con il materiale desiderato e il successivo disegno delle celle da parte di un
laser.
Silicio amorfo depositato da fase vapore: hanno un'efficienza bassa (8%), ma sono molto più
economiche da produrre. Il silicio amorfo (Si-a) possiede un bandgap maggiore del silicio
cristallino (Si-c) (1,7 eV contro 1,1 eV): ciò significa che è più efficiente nell'assorbire la parte
visibile dello spettro della luce solare, ma meno efficace nel raccoglierne la parte infrarossa.
Dato che il silicio nanocristallino (con domini cristallini dell'ordine del nanometro) ha circa lo
stesso bandgap del Si-c, i due materiali possono essere combinati creando una cella a strati, in
cui lo strato superiore di Si-a assorbe la luce visibile e lascia la parte infrarossa dello spettro alla
cella inferiore di silicio nanocristallino.
21
CIS: basate su strati di calcogenuri (ad es. Cu(InxGa1-x)(SexS1-x)2). Hanno un'efficienza fino
all'11%, ma il loro costo è ancora troppo elevato.
Celle fotoelettrochimiche: queste celle, realizzate per la prima volta nel 1991, furono
inizialmente concepite per imitare il processo di fotosintesi. Questo tipo di cella permette un
uso più flessibile dei materiali e la tecnologia di produzione sembra essere molto conveniente.
Tuttavia, i coloranti usati in queste celle soffrono problemi di degrado se esposti al calore o alla
luce ultravioletta. Nonostante questo problema, questa è una tecnologia emergente con un
impatto commerciale previsto entro una decina di anni.
Cella fotovoltaica ibrida: combina i vantaggi dei semiconduttori organici e di vari tipi di
semiconduttori inorganici.
Cella fotovoltaica a concentrazione: unisce alle tecnologie di cui sopra, delle lenti a
concentrazione solare che aumentano sensibilmente l'efficienza. Rappresentano la nuova
promettente generazione di pannelli ancora in fase di sviluppo.
Moduli cristallini
Silicio monocristallino, in cui ogni cella è realizzata a partire da un wafer la cui struttura
cristallina è omogenea (monocristallo), opportunamente drogato in modo da realizzare
una giunzione p-n;
Silicio policristallino, in cui il wafer di cui sopra non è strutturalmente omogeneo ma
organizzato in grani localmente ordinati.
Moduli a film sottile
Fig 2.5: Modulo a film sottile
Silicio amorfo, in cui gli atomi di silicio vengono deposti chimicamente in forma amorfa, ovvero
strutturalmente disorganizzata, sulla superficie di sostegno. Questa tecnologia impiega quantità
molto esigue di silicio (spessori dell'ordine del micron). I moduli in silicio amorfo mostrano in
genere una efficienza meno costante delle altre tecnologie rispetto ai valori nominali, pur avendo
garanzie in linea con il mercato. Il dato più interessante riguarda l'EROEI, che fornisce valori molto
alti (in alcuni casi arrivano anche a 9), il che attesta l'economicità di questa tecnologia
22
Tellururo di cadmio (CdTe): sono i pannelli a film sottile più economici e col più basso
rendimento termodinamico. A Maggio 2011, il Consiglio d'Europa ha confermato che non
esiste alcun divieto di produzione o installazione di questi pannelli, allo scopo di rispettare gli
obiettivi prefissati in termini di energie rinnovabili ed efficienza energetica; contestualmente,
data la sua documentata tossicità, ha inserito il cadmio nella lista dei materiali vietati nelle
produzioni elettriche o elettroniche. Il divieto di utilizzo nella produzione di celle fotovoltaiche
parte dal 2013 (modifica alla Direttiva: Restriction of Hazardous Substances Directive del 24
Novembre 2010).
Solfuro di cadmio (CdS) microcristallino, che presenta costi di produzione molto bassi in
quanto la tecnologia impiegata per la sua produzione non richiede il raggiungimento delle
temperature elevatissime necessarie invece alla fusione e purificazione del silicio. Esso viene
applicato ad un supporto metallico per spray-coating, cioè viene letteralmente spruzzato come
una vernice. Tra gli svantaggi legati alla produzione di questo genere di celle fotovoltaiche vi è
la tossicità del cadmio ed il basso rendimento del dispositivo.
Arseniuro di gallio (GaAs), una lega binaria con proprietà semiconduttive, in grado di
assicurare rendimenti elevatissimi, dovuti alla proprietà di avere un gap diretto (a differenza del
silicio). Viene impiegata soprattutto per applicazioni militari o scientifiche avanzate (come
missioni automatizzate di esplorazione planetaria o fotorivelatori particolarmente sensibili).
Tuttavia il costo proibitivo del materiale monocristallino a partire dal quale sono realizzate le
celle, lo ha destinato ad un impiego di nicchia.
Diseleniuro di indio rame (CIS), con opacità variabile dal 100% al 70% ottenuta mediante fori
ricavati direttamente nel film.
Diseleniuro di indio rame gallio (CIGS)
2.6 Varianti proprietarie
Eterogiunzione, letteralmente giunzione tra sostanze diverse, in cui viene impiegato uno strato
di silicio cristallino come superficie di sostegno di uno o più strati amorfi o cristallini, ognuno
dei quali ottimizzato per una specifica sotto-banda di radiazioni;
Silicio microsferico, in cui si impiega silicio policristallino ridotto in sfere del diametro di circa
0,75 mm ingabbiate in un substrato di alluminio;
Delle tecnologie citate, soltanto l'amorfo e il microsferico permettono la flessione del modulo: nel
caso dell'amorfo non vi è la struttura cristallina del materiale ad impedirne la flessione, nel caso del
microsferico non è la cella (sfera) a flettersi, ma la griglia a nido d'ape su cui è disposta.
23
2.7 Tolleranza
La tolleranza di fabbricazione è un dato percentuale (generalmente variabile dal ±3% al ±10%) che
ogni produttore dichiara in relazione ai propri standard qualitativi di produzione. Tanto minore è la
tolleranza dichiarata, tanto più stabili nel tempo e predicibili saranno le prestazioni elettriche del
modulo, a parità di condizioni di utilizzo.
Nella maggior parte dei casi, i produttori realizzano più versioni dello stesso modulo, distinte in
base alla potenza nominale, pur realizzandoli con le medesime celle, che vengono preventivamente
raggruppate in famiglie prestazionali simili. L'obiettivo dell'operazione è gestire in modo più
accorto possibile le celle elettricamente peggiori, che potrebbero inficiare le prestazioni dell'intero
modulo.
In quest'ottica quindi, tanto più numerose sono le famiglie di celle uniformi, tanto
minore potrebbe essere la tolleranza di fabbricazionegarantita. Nella realtà di mercato, tuttavia, data
la curva di Gauss che descrive la distribuzione statistica della qualità di tutte le celle fotovoltaiche
di una data partita produttiva, le linee di separazione tra gruppi di moduli simili si ampliano a volte
fino a costituire fasce piuttosto ampie.
Il produttore può così gestire la parte di produzione all'interno di queste fasce:
1. declassando il prodotto in questione, per considerarlo entro la tolleranza positiva del modulo
inferiore, con il risultato di perdere profitto;
2. innalzando il prodotto, per considerarlo entro la tolleranza negativa del modulo superiore,
con il risultato di marginalizzare di più a discapito della qualità effettiva del prodotto.
Dal punto di vista commerciale, il produttore si garantisce la liceità dell'operazione dichiarando una
tolleranza di fabbricazione più ampia del necessario rispetto alle potenze nominali dei vari moduli
realizzati. L'immediato effetto che questa pratica comporta è la ricaduta di cospicue quantità di
moduli all'interno delle citate fasce a cavallo di due o più tolleranze di fabbricazione.
Alla luce di ciò, i moduli fotovoltaici qualitativamente migliori sono da ricercarsi tra quelli che
combinano:
una tolleranza negativa stretta (quella positiva può considerarsi trascurabile);
una nulla o limitata area di sovrapposizione tra le fasce di tolleranza delle varie potenze dello
stesso modulo.
L'artificio della tolleranza più ampia del necessario è una tecnica impiegata solo da produttori
minori, a causa della sua facile individuazione (basta una brochure con la lista dei prodotti trattati e
una calcolatrice) e del sospetto che inevitabilmente farebbe sorgere nei confronti del produttore.
2.8 Certificazioni
I moduli fotovoltaici, se impiegati in un impianto fotovoltaico connesso alla rete all'interno
dell'Unione Europea, devono obbligatoriamente essere certificati in base alla normativa IEC 61215,
che ne determina le caratteristiche sia elettriche che meccaniche. Tra i test più importanti si cita
quello per determinarne la potenza in condizioni di insolazione standard, espressa in watt
picco (Wp).
24
2.10 Costi
Oltre ai problemi di efficienza e tolleranza un discorso a parte meritano i costi di realizzazione delle
celle fotovoltaiche, dei relativi moduli e impianti. Per quanto riguarda le celle fotovoltaiche i costi
sono gravati fino a circa il 33% dal materiale (ad es. silicio) comprendendo gli scarti di lavorazione
e il costoso processo di purificazione (in generale sui costi del materiale di base pesa anche la sua
reperibilità fisica in natura per riuscire ad ottenere un'economia di scala opportuna, ma non è questo
il caso del silicio che è altresì abbondante sulla crosta terrestre).
Vanno aggiunti poi i restanti costi per i processi di realizzazione della cella fotovoltaica.
Ragionando in termini di moduli fotovoltaici, ai costi della cella solare si devono aggiungere i costi
della realizzazione dei moduli interi ovvero dei materiali assemblanti, della messa in posa a terra
tramite materiali, dell'elettronica di potenza necessaria (inverter), della progettazione, della
manodopera e della manutenzione. Sommato il tutto si giunge ad un costo indicativo di circa 0.75
€/Wp installato.
Considerando una producibilità media degli impianti installati in Italia pari a 1200 kWh/kWp
all'anno, e che la vita di un impianto fotovoltaico è superiore a 20 anni, il costo dell'energia prodotta
dai moduli fotovoltaici è indicativamente di 12/16 centesimi di euro per kilowattora prodotto, il che
ci indica che questa tecnologia, che per diverso tempo ha avuto costi abbastanza superiori ad altre
fonti energetiche, è ormai competitiva allo stesso livello delle altre fonti fossili. Come incentivo alla
realizzazione di impianti fotovoltaici è attivo in Italia il sistema Conto Energia.
In definitiva il parametro complessivo di qualità che caratterizza un modulo fotovoltaico è il
rapporto costo/efficienza o equivalentemente il costo per kilowattora prodotto.
2.11 I prodotti in commercio
I moduli fotovoltaici in silicio cristallino più comuni hanno dimensioni variabili da 0,5 m² a 2,0 m²,
con punte di 2,5 m² in esemplari per grandi impianti. Non vi è comunque particolare interesse a
costruire moduli di grandi dimensioni, a causa delle grosse perdite di prestazioni che l'intero
modulo subisce all'ombreggiamento (o malfunzionamento) di una sua singola cella.
La potenza più comune si aggira intorno ai 230 Wp a 32 V, raggiunti in genere impiegando 60 celle
fotovoltaiche (il modulo da 60 celle in silicio policristallino è il più utilizzato in Italia e copre circa
il 90% dei moduli). La superficie occupata dai modelli commerciali si aggira in genere intorno ai
7,2 m2/kWp, ovvero sono necessari circa 7,2 metri quadrati di superficie per ospitare pannelli per un
totale nominale di 1.000 Wp. I migliori moduli in commercio raggiungono un'efficienza del 19,6%
e richiedono quindi una superficie di 5,147 metri quadrati per 1.000 Wp.
Dopo un biennio di instabilità, i costi al cliente finale del modulo installato sul tetto si sono
stabilizzati nella fascia 3,50/5,00 €/Wp a seconda delle dimensioni dell'impianto (ad aprile 2011).
Va evidenziato che questo valore è suscettibile di scostamenti sostanziali a seconda del punto di
rilevazione all'interno della filiera del prodotto. Il prezzo sopra indicato è da considerarsi come
prezzo del modulo installato sul tetto di una residenza abitativa, mentre il prezzo dei moduli in
silicio policristallino da 60 celle finito pronto ad essere installato di buona qualità si aggira tra i
1,50/2,00 €/Wp
Nei parchi solari il costo del modulo installato tende ad essere compreso tra i 2,50/3,50 €/Wp
La generale instabilità dei prezzi del biennio 2004/2005 era stata causata dall'improvviso squilibrio
tra domanda e offerta conseguente al lancio contemporaneo delle politiche di incentivazione
25
dellefonti rinnovabili da parte dei paesi ratificanti il Protocollo di Kyōto. Essendo il prezzo del
modulo fotovoltaico in silicio mono o policristallino legato in gran parte al costo delle celle (le celle
incidono per circa il 75% nel totale delle materie impiegate per la realizzazione del modulo) nei
primi mesi del 2011 si è assistito ad un calo dei prezzi delle celle dovuto alla diminuzione degli
incentivi da parte della Germania e dell'Italia.
2.12 Riciclaggio del pannello
La maggior parte dei componenti di un modulo solare possono essere riutilizzati. Grazie alle
innovazioni tecnologiche verificatesi negli ultimi anni, fino al 95% di alcuni materiali
semiconduttori o di vetro, così come vaste quantità di metalli ferrosi e non ferrosi impiegati nei
moduli fotovoltaici possono essere recuperati. Alcune aziende private e organizzazioni non-profit,
come PV CYCLE nell'Unione Europea, sono impegnate in operazioni di raccolta e riciclaggio alla
fine del ciclo di vita dei moduli.
Due delle soluzioni di riciclaggio più comuni sono:
Moduli a base di silicio: i telai in alluminio e le scatole di derivazione sono smontati
manualmente all'inizio del processo. Il modulo viene quindi schiacciato in un mulino e le
diverse frazioni sono separate - vetro, plastica e metalli. È possibile recuperare più dell’80% del
peso in entrata ed il vetro misto ottenuto, per esempio, è facilmente accettato dall'industria del
vetro espanso e del vetro isolante. Questo processo può essere eseguito da riciclatori di vetro
piano poiché la morfologia e la composizione di un modulo fotovoltaico sono simili a quelle
che i vetri piani impiegano nell'industria edile e automobilistica.
Moduli non a base di silicio: Tecnologie di riciclaggio specifiche per i moduli fotovoltaici non a
base di silicio sono state sviluppate; alcune di esse fanno uso di bagni chimici al fine di separare
i diversi materiali semiconduttori. Per i pannelli al tellururo di cadmio, il processo di riciclaggio
inizia schiacciando il modulo e successivamente separando le diverse frazioni. Questo processo
di riciclaggio è progettato per recuperare fino al 90% del vetro e il 95% dei materiali
semiconduttori contenuti. Alcuni impianti di riciclaggio su scala commerciale sono stati creati
negli ultimi anni da aziende private.
A partire dal 1 luglio 2012 i produttori di pannelli fotovoltaici devono possedere l'attestato di
adesione a un consorzio che garantisca il riciclo dei moduli fotovoltaici[6]. In mancanza di tale
adesione, comprovata dal relativo attestato da esibire all’atto della vendita, il produttore non
potrà permettere al proprio cliente di usufruire degli incentivi. I requisiti che il
consorzio/sistema deve soddisfare per garantire la gestione del fine vita dei moduli fotovoltaici
installati sugli impianti in esercizio a partire dal 1° luglio 2012 sono stati stabiliti dal GSE
(Gestore dei Servizi Energetici) nella terza revisione delle "Regole Applicative per il
riconoscimento delle tariffe incentivanti previste dal DM 5 maggio 2011", IV Conto Energia.
26
2.13 Ricerca e innovazioni
La ricerca in campo fotovoltaico è indirizzata verso il miglioramento del rapporto fra efficienza e
costo del modulo fotovoltaico. Il basso valore di questo rapporto costituisce il limite più forte
all'affermazione su grande scala di questa tecnologia energetica il che si traduce in un alto costo per
kilowattora prodotto almeno nel periodo di ammortamento dell'impianto. Quindi la ricerca si
indirizza verso la scoperta di materiali semiconduttori e tecniche di realizzazione che coniughino il
basso costo con un'alta efficienza di conversione.
Presso l'Università di Toronto nel 2005 è stato inventato un materiale plastico che
sfrutta nanotecnologie per convertire in elettricità i raggi solari anche nella banda dell'infrarosso, e
che quindi funziona anche con il tempo nuvoloso[7]. Gli autori della ricerca sperano che costruendo
pannelli fotovoltaici con questo materiale si possano ottenere prestazioni cinque volte superiori al
silicio, tanto che una copertura dello 0,1% della superficie terrestre sarebbe sufficiente a sostituire
tutte le attuali centrali elettriche. Il materiale può essere spruzzato su una superficie, come un
vestito o la carrozzeria di un'automobile.
Un'importante collaborazione fra Eni e Mit sta orientando gli investimenti nella costruzione di celle
fotovoltaiche[8] con materiali che ne aumentino il rendimento rispetto al 15-17% attuale del silicio.
La società cinese Suntech Power Holdings, una delle società leader al mondo, nel piano industriale
di dicembre 2010[9] ha stimato di raggiungere nel 2015 un'efficienza di conversione su larga scala
pari al 23%.
Il neonato fotovoltaico organico consente un abbattimento dei costi, pur senza aumento di
efficienza. Questa tecnologia usa pigmenti organici al posto dei semiconduttori inorganici e può
sfruttare economiche tecniche realizzative di fotolitografia.
27
Capitolo 3
Il lavoro svolto in questo progetto di tesi consiste nel raccogliere un insieme di misure ambientali
attraverso un pannello fotovoltaico e di svolgere due tipi di operazioni su di esso:
-valutazione della veridicità dei dati ottenuti: è stato necessario prima di tutto “ripulire” l’insieme
dei campioni da eventuali in correttezze intrinseche alla misurazione da parte dello strumento;
-elaborazione dei dati: questa fase comprende sia il calcolo di varie grandezze quali la potenza
stimata e la costruzione dei vari algoritmi che vedremo in seguito ( LMSE, previsione e
addestramento tramite MLP).
3.1 Terminologia
I dati ambientali vengono raccolti dal pannello fotovoltaico in un arco di tempo che va dalle ore
07.00 di mattina alle ore 17.30 di sera. Questa operazione viene ripetuta ogni giorno per tutti i mesi
dell’anno.Le grandezze raccolte direttamente tramite pannello fotovoltaico sono le seguenti:
-Vm: tensione del modulo
-Im: corrente del modulo
-Pm: potenza del modulo
-Gm: irradiazione solare misurata sulla superficie del modulo
-Gh: irradiazione globale orizzontale
-Gdh: irradiazione diffusa orizzontale
-Tm: temperatura del modulo
-Ta: temperatura dell’ambiente di lavoro
-Istante di rilevazione
Per la rilevazione delle grandezze ambientali appena citate sono stati utilizzati due tipi diversi di
pannelli fotovoltaici: Isofoton e Sharp. E’ sottinteso che tali parametri variano sia a seconda
dell’istante di rilevazione sia a seconda del pannello considerato. Una volta effettuate le
misurazioni, tutti i dati vengono salvati in una tabella excel per essere poi controllati ( è possibile
che lo strumento fornisca dati inaffidabili o errati), selezionati(considerando un solo campione ogni
mezzora) , elaborati attraverso il calcolo del rendimento percentuale stimato e successivamente
utilizzati come ingressi per i metodi di lavoro LMSE e MLP.
28
3.2 Metodo LMSE
L’algoritmo Least Mean Square ( Minimi Quadrati) è stato applicato alla formula dell’errore
quadratico medio ( da qui LMSE o Least Mean Square Error) per poterlo minimizzare. L’algoritmo
è lineare e presenta una notevole semplicità di implementazione, infatti è stato sviluppato
direttamente sul foglio excel contenente i dati ambientali, senza il bisogno di dover ricorrere al
codice Matlab. Per prima cosa è stato necessario calcolare alcuni parametri che ci consentono di
ricavare la formula completa dell’errore quadratico medio. La prima grandezza stimata è il rapporto
di irradiazioni R, definito per ogni campione del pannello fotovoltaico nel seguente modo:
ℎ
ℎ
=
dove Gdh è l’irradiazione diffusa orizzontale sul modulo e Gh è l’irradiazione globale orizzontale.In
secondo luogo è stato necessario calcolare il rendimento percentuale effettivo del modulo
fotovoltaico attraverso la formula:
% = 100
che include la potenza del modulo Pm, l’area Am del modulo e l’irradiazione Gm sul modulo. A
questo punto non resta che definire il rendimento percentuale stimato nel seguente modo:
% =
+ !"
# + $% +
1000
e andare a sottrarre questa quantità al rendimento percentuale effettivo calcolato in precedenza:
= (100
−
− !(
/1000)– $% –
)
Elevando al quadrato il risultato ottenuto otteniamo la formula dell’errore quadratico medio:
*
=(
%−
% )* = (100
− − !(
/1000)– $% –
)
*
nella quale i coefficienti a,b,c,d vengono determinati con il metodo LMS. Per prima cosa calcolo le
derivate prime dell’equazione sopra citata per ognuna delle incognite a,b,c,d e le eguaglio a zero:
+
+
*
+
+
*
= 2"
= 2"
+ *
= 2"
+$
%−
%−
−
%−
−
!"
−
!"
# − $% −
1000
1000
!"
# − $% −
1000
# (−1) = 0
# "− ! "
# − $% −
1000
## = 0
# (−% ) = 0
29
+
+
*
= 2"
%−
−
!"
# − $% −
1000
# (− ) = 0
Dopodiche, per ogni equazione, separo i termini noti dalle incognite portando a primo membro tutti
quei termini che non contengono a,b,c,d. Ottengo quindi un sistema di equazioni del tipo:
∆
1=
∆
3 = % + 〖% !〗(
∆
∆
+ !(
2 = !(
/1000) + 〖( !(
4=
!(
+
I termini noti ∆
∆
/1000) + $% +
1=
/1000))〗^2 + $% (
/1000) + $〖% 〗^2 +
/1000) + $%
+
^2
% /1000) +
(
/1000)
contengono i termini noti delle rispettive equazioni e valgono:
%;∆
2=
23
% ! 145556 ; ∆
3=% %;∆
2= %
Una volta ricavato il sistema sopra esposto, vado a calcolare i valori medi delle grandezze
componenti i termini noti e i coefficienti delle incognite e li inserisco nelle equazioni in modo di
ottenere un nuovo sistema che, invece di valori singoli, ha come termini e coefficienti dei valori
medi calcolati sull’intero set di misurazioni ottenute tramite il pannello fotovoltaico. Ottengo
quindi:
Da questo sistema è possibile ricavare le matrici dei coefficienti necessarie per definire le
quattroincognite. Si tratta di quattro matrici 4x4 così composte:
30
La prima matrice indicata con ∆ contiene sulla prima colonna tutti i coefficienti dell’incognita a
delle diverse equazioni. La seconda, la terza e la quarta riportano rispettivamente i coefficienti di b,
c e d delle equazioni componenti il sistema. Per calcolare il valore di a,b,c,d sostituisco la colonna
dei coefficienti di una determinata incognita con quella dei termini noti, calcolo il determinante
della matrice ottenuta e lo divido per il determinante della matrice:
per quanto riguarda il determinante della matrice relativa all’incognita a. I restanti determinanti
vengono calcolati analogamente:
31
Calcolati i determinanti delle matrici modificate e della matrice ∆ possiamo ricavare le incognite
con semplici passaggi matematici:
=
789 ∆:
;<=∆
;
=
789 ∆>
;<=∆
;$
=
789 ∆?
;<=∆
;
=
789 ∆;
;<=∆
Una volta note le incognite possiamo calcolare l’errore quadratico semplicemente applicando la
ormai nota formula:
*
=(
%−
% ) = (100
*
− − !(
/1000)– $% –
)
*
e constatare che il metodo ai minimi quadrati non fornisce una minimizzazione dell’errore
efficiente. Infatti si ottiene un errore quadratico medio pari a 1.71 e considerato il fatto che
mediamente il rendimento percentuale effettivo di un pannello fotovoltaico mediamente si aggira
intorno a 7.42 (per Isofoton) o a 8,2 (per Sharp), commetteremmo un incertezza nella stima dei
valori di rendimento che va oltre il 10%, risultato sicuramente migliorabile.
E’ necessario quindi adottare altri sistemi di minimizzazione dell’errore nella stima delle grandezze
relative al modulo fotovoltaico. Nel capitolo seguente discuteremo l’efficienza dell’utilizzo di una
rete MLP, quindi di un sistema non lineare, per raggiungere questo obiettivo.
32
3.3 MLP (non lineare)
Una volta constatato lo scarso rendimento di un sistema lineare di riduzione dell’errore di
previsione, si è deciso di passare all’utilizzo di un sistema non lineare ovvero il percettrone
multistrato. Nel corso di questo progetto sono state sviluppate tre diverse tipologie di MLP, per
cercare di capire quale delle tre proponesse risultati migliori. Per ognuna di queste tre categorie,
sono stati effettuati tentativi di stima variando il numero e il tipo degli ingressi. Inizialmente, per
semplicità mi sono limitato a inserire nella rete solo le grandezze Gm e Tm. Successivamente, è
stato introdotto un terzo ingresso che inizialmente era costituito dalla grandezza Gdh e,
successivamente, è stato sostituito con il rapporto Gdh/Gh. Quest’ultimo, per comodità nella
scrittura del codice e degli algoritmi di calcolo, è stato indicato con il simbolo R.
L’algoritmo di funzionamento della rete (implementato tramite codice MATLAB) è lo stesso per
tutte e tre le diversi topologie di rete, con la differenza che il numero di calcoli matematici e la loro
complessità ( e di conseguenza l’affidabilità dei risultati) cresce con le dimensioni della rete
neurale. Innanzitutto vengono estratti dalle tabelle excel i dati che fungeranno da ingressi alla rete e
vengono memorizzate in array. Vengono poi create delle matrici di pesi casuali relativi ai
collegamenti tra i vari neuroni componenti gli strati della rete per poi passare ad una fase di
addestramento della rete (ripetuta per più sessioni sul 75% dei valori di ingresso) nella quale viene
calcolato il campo indotto sui nodi di ogni strato, partendo da quello di ingresso e arrivando a quello
di uscita attraverso gli eventuali strati nascosti. Viene in seguito effettuata una valutazione
dell’errore di stima con conseguente aggiornamento dei pesi della rete per ridurre l’errore stesso.
Una volta aggiornati i pesi sinaptici della rete, ha inizio una nuova sessione di addestramento che
svolge le stesse operazioni della precendente, ma con una matrice dei pesi aggiornata.
Finita la parte relativa all’addestramento della rete, la rete MLP è in grado di effettuare una
previsione dei valori di rendimento percentuale PR% del modulo fotovoltaico, con un errore che è
stato minimizzato grazie alla fase precedente.
Vediamo ora nel dettaglio le due fasi appena descritte e le operazioni matematiche che le
compongono.
33
-Fase di addestramento
Figura 3.1: Schema di funzionamento dell’algoritmo di addestramento
In ingresso alla rete neurale viene mandato un set di dati di input costituente il 75% dei campioni
totali disponibili nella tabella excel. Innanzitutto viene calcolata una matrice dei pesi casuale di
partenza (i cui valori hanno lo stesso ordine di grandezza degli ingressi) dopodiche viene stabilito il
campo indotto nei vari strati.. Prima di tutto devo ricavare il parametro s attraverso la seguente
formula:
DA = E E @AB CB
A
B
Dove @AB rappresenta il valore della matrice dei pesi relativo al peso sinoptico del collegamento tra
l’ingressi i-esimo di valore CB e il nodo j-esimo
j esimo dello strato (sia esso nascosto o di uscita).
Inserendo tale parametro nella formula del campo indotto ricavo facilmente:
(1
FB = GHDA I =
&1
J*K
(
J*K (
Con il calcolo del campo indotto si conclude quella serie di operazioni che vengono
vengo svolte “in
avanti” ovvero eseguite partendo dallo strato di ingresso e muovendosi verso lo strato di uscita,
attraversando gli eventuali strati nascosti. Inizia poi una serie di calcoli che si svolge all’indietro”
ovvero dallo strato di uascita a quello di ingresso, tramite quindi la tecnica di BACK
PROPAGATION. Prima di tutto viene effettuata una valutazione dell’errore, calcolato come la
differenza tra la grandezza di uscita stimata (nel nostro caso il rendimento percentuale stimato) e la
grandezza di uscita effettiva( ottenuta mediante i semplici calcoli matematici). Il calcolo dell’errore
avviene nel seguente modo:
L
FL∗
FL
34
dove FL∗ FL rappresentano rispettivamente la grandezza di uscita stimata ed effettiva calcolate per
il nodo h-esimo dello strato di uscita. Questa quantità è nota anche come ERRORE DI
ADDESTRAMENTO. Il suo elevamento al quadrato ci consente di ottenere un parametro molto
importante per la valutazione dell’affidabilità dell’intera rete. Questa quantità è chiamata ERRORE
QUADRATICO DI ADDESTRAMENTO:
L
= (FL∗ − FL )*
L’errore viene poi valutato in tutti gli strati nascosti ( dal piu vicino all’output fino ad arrivare al
più lontano) grazie al calcolo di un coefficiente di variazione del peso sinapticoGA definito come:
GA =
L
∗ D N (DL ) = L
∗ (1 + OL ) ∗ (1 − OL )
dove OL è il valore di campo indotto in uscita allo strato i-esimo. Nota questa quantità è possibile
andare a valutare l’errore nello strato successivamente adiacente nel seguente modo:
A
= E E GL @LA
L
A
che tiene conto di tutti i coefficienti di variazione del peso sinaptico relativi a tutti i collegamenti
esistenti tra i due strati e la matrice dei pesi di tali collegamenti. Lo stesso procedimento si ripete
poi per i restanti strati fino a quello di input.
Un’altra operazione molto importante che effettuata con tecnica di BACK PROPAGATION è la
procedura di aggiornamento dei pesi, che avviene tramite il calcolo della variazione del peso di tutti
i collegamenti sinaptici:
∆@LA = −PGL FA
che non è altro che il prodotto tra la costante P(nell’ordine di 10Q ), il coefficiente di variazione del
peso sinaptico relativo al collegamento h-esimo e l’uscita del j-esimo nodo dello strato adiacente.
35
Figura 3.2: Funzionamento della Back Propagation
Propagati
Una volta esaurito il ciclo di addestramento e aggiornato in modo ottimale le matrici dei pesi, è
possibile passare alla fase di previsione del restante 25 % dei valori.
-Fase di previsione dei valori
Come per la fase precedente, viene calcolato il campo indotto in ogni strato, da quello di input fino
a quello di output, passando per tutti gli eventuali strati nascosti. L’unica differenza dalla sessione
di addestramento sta negli ingressi. Nella fase di training venivano inseriti nella rete il 75% dei
de
campioni totali elaborati e convalidati. Nella fase di previsione gli ingressi sono costituiti dal
restante 25% di tale insieme di valori. I calcoli del campo indotto sono i medesimi e vengono svolti
“in avanti” fino ad ottenere il valore di output della rete che, come già visto, ha la seguente
espressione:
(1
FB = GHDA I =
&1
J*K
(
J*K (
Nel nostro caso, questa grandezza sarà rappresentata dal rendimento percentuale.
36
3.4 Risultati ottenuti
Implementando un codice Matlab che svolga le funzioni della rete MLP appena descritte, è stato
possibile inviare alla rete gli le grandezze ambientali rilevate dai due moduli forovoltaici Isofoton e
Sharp. Come già detto in precedenza si è preferito fare diverse prove con un diverso numero di
ingressi e di strati nascosti per confrontare i vari comportamenti delle reti e soprattutto l’andamento
dell’errore quadratico al susseguirsi delle sessioni di addestramento. I risultati ottenuti sono esposti
sottoforma di grafici, prima di tutto per chiarezza di esposizione, in secondo luogo per evitare di
riportare lunghe tabelle di valori ingombranti e poco chiare.
-MLP senza strati nascosti
Analizzando il caso più semplice, ovvero quello di due ingressi Gm e Tm, si nota che l’andamento
dell’errore quadratico di addestramento è piuttosto casuale. Anche se di per se l’errore assume
valori sicuramente più accettabili rispetto a quelli ottenuti con LMSE, la rete non è ancora in grado
di fornire una minimizzazione accettabile dell’errore. I risultati delle prove effettuate sulla rete base
senza strati nascosti con una fase di training composta da 100 sessioni sono riportati di seguito:
Figura 3.3: Andamento dell’errore quadratico nella rete senza strati nascosti (Gm,Tm)
37
Nel grafico riportato in figura 3.3 sono mostrati i valori dell’errore quadratico di addestramento al
susseguirsi delle 100 sessioni di training nel caso in cui gli ingressi della rete siano Gm e Tm. Si
nota innanzitutto che assume valori molto più piccoli rispetto a quelli ottenuti con i metodi lineari,
anche se a valori quasi nulli di errore, se ne alternano alcuni più grandi. Nei restanti casi a tre
ingressi i risultati sono simili, come previsto, dal momento che non è ancora stata inserito nessuno
strato nascosto che introduca una minimizzazione significativa. Sono riportati di seguito i grafici del
caso in cui gli ingressi della rete sono Gm,Tm,Gdh:
Figura 3.3: Andamento dell’errore quadratico nella rete senza strati nascosti (Gm,Tm,Gdh)
38
e nel caso in cui gli input siano Gm,Tm,R:
Figura 3.3: Andamento dell’errore quadratico nella rete senza strati nascosti (Gm,Tm,R)
Tuttavia, va detto che i valori di errore sono comunque accettabili perché molto piccoli quindi,
anche nella sua forma elementare, la rete neurale costituisce un buon metodo di previsione dei
valori del pannello, anche se l’errore non viene praticamente minimizzato.
39
-MLP con uno strato nascosto
In questo caso viene inserito uno strato nascosto composto da 3 nodi nascosti. Si nota subito dai
grafici
rafici che i valori dell’errore quadratico, non solo è minore fin dalla prima stima, ma viene anche
minimizzato al passare delle sessioni di addestramento. I risultati sono riportati nei tre grafici
seguenti per gli ingressi (Gm,Tm) , (Gm,Tm,Gdh) , (Gm,Tm,R):
(Gm,Tm,
Figura 3.6:: Andamento dell’errore quadratico
quadratic nella rete con uno strato nascosto
nascost (Gm,Tm)
40
Figura 3.7:: Andamento dell’errore quadratico nella rete con uno strato nascosto
nascost (Gm,Tm,Gdh)
41
Figura 3.8:: Andamento dell’errore quadratico nella rete con uno strato nascosto
nascost (Gm,Tm,R)
42
-MLP con due strati nascosti
Inserendo un secondo strato nascosto composto da dieci nodi otteniamo risultati molto interessanti.
Il valore dell’errore si abbassa ancora e avviene una minimizzazione molto efficiente. Si noti che sia
in questo caso, sia nel caso precedente, il numero di sessioni di training è stato ridotto da 100 a 40,
per rendere più veloce l’implementazione del codice da parte di Matlab, conservando tuttavia
l’efficienza correttiva dell’algoritmo. Sono riportati di seguito i grafici relativi ai diversi set di input
(Gm,Tm),
,Tm), (Gm,Tm,Gdh) e (Gm,Tm,R):
Figura 3.9:: Andamento dell’errore quadratico
quadratic nella rete (Gm,Tm) con due strati nascosti
43
Figura 3.10: Andamento dell’errore quadratico nella rete (Gm,Tm,Gdh) con due strati nascosti
44
Figura 3.11: Andamento dell’errore quadratico
quadratic nella rete (Gm,Tm,R) con due strati nascosti
3.5 Conclusioni
Una volta terminata la fase di addestramento e minimizzato l’errore quadratico, si può passare alla
fase di previsione dei valori nella quale avviene la stima vera e propria del rendimento che il
pannello fotovoltaico avrà per il restante 25% di campioni in
in ingresso. Questa fase consiste
semplicemenente nel calcolo del campo indotto dei vari strati componenti la rete attraverso le
45
formule matematiche già esposte in precedenza, fino ad arrivare ad avere un valore di output
rappresentato dal valore del rendimento percentuale che la rete ha previsto per un determinato set di
input. L’unica differenza tra questa fase e la precedente fase di training sta nel fatto che non viene
ricalcolata da zero una matrice dei pesi sinaptici casuale relativa ai collegamenti dei noti della rete,
ma viene utilizzata la matrice aggiornata durante l’ultima sessione di addestramento, cosicchè la
previsione sia il più precisa possibile.
46
Ringraziamenti
Prima di tutto vorrei ringraziare il professor Brofferio, che si è rivelato un ottimo referente nei casi
di necessità ed ha sempre avuto una risposta chiara per ogni mio dubbio. Inoltre gli sono grato per
avermi fatto conoscere un mondo affascinante come quello delle reti neurali e quello della
tecnologia fotovoltaica, mondi nei quali desidero fortemente proseguire la conoscenza in ambito
lavorativo.
Un grande ringraziamento va a tutti i miei famigliari e parenti, in modo particolare i miei genitori e
mia sorella, che hanno saputo darmi la giusta motivazione per portare a termine il mio percorso
formativo anche nei momenti più difficili, ai miei amici che non vedono l’ora di festeggiare con me
una tappa così importante della mia vita e alla mia ragazza, fonte inesauribile di incoraggiamenti.
Una piccola dedica a quelle persone care che mi hanno cresciuto ma che purtroppo non ci sono più.
Maria e Ferdinando questo scritto è per voi. Avete contribuito in modo fondamentale allo sviluppo
della persona che sta scrivendo queste parole. Grazie di cuore.
Fabio Riccò
47
Bibliografia
Simon Haykin- “Neural Networks, a comprehensive foundation”
Liena Vilde – “Modeling a PV Module Using Matlab”
F.Almonacid,L.Hontoria, J.Aguilera, G.Nofuentes – “Characterisation of PV Modules based
in artificial neural networks”
L.Fanni, A.Virtuani, D.Chianese “Sensational power fluctuations of single junction
amorphous silicon modules”
T.Hiyama, K.Kitabashi – “Neural network based estimation of maximum power generation
from PV module using environmental information”
G.Friesen,D. Chianese, I.Pola, A.Realini, A.Bernasconi – “Energy rating measurements and
predictions at Isaac”
48