Capitolo
5
La termodinamica
del secondo principio
1. Il motore termico
Come possiamo riassumere quanto detto sinora sul calore e sul lavoro?
Calore e lavoro sono due processi tramite i quali avviene trasferimento di energia
fra un sistema e l’ambiente. Il lavoro L rappresenta l’energia scambiata
attraverso dei mezzi meccanici, vale a dire per effetto dello spostamento del
punto di applicazione delle forze con cui il sistema interagisce con l’ambiente. Il
calore Q rappresenta l’energia scambiata a causa della differenza di temperatura
fra il sistema e l’ambiente. Mai si dirà che un sistema possiede del lavoro oppure
che un sistema possiede del calore. Q e L non sono proprietà dei sistemi ma
piuttosto quantità in trasferimento: il loro valore descrive il processo di scambio di
energia, e varia a seconda delle modalità del trasferimento.
Cosa s’ intende con il termine motore termico?
Con il termine macchina termica o motore termico intendiamo un dispositivo che
riceve energia sotto forma di calore e ne restituisce una parte sotto forma di
lavoro.
1
Il calore può essere ricevuto dal motore sia attraverso il contatto con una
sorgente termica a temperatura maggiore della sua, sia a spese dell’energia
interna di qualche sostanza, come avviene durante una reazione chimica. Un
esempio di questo secondo caso è la combustione della benzina.
Come possiamo trasformare calore in lavoro?
La risposta a questa fondamentale domanda venne dallo studioso francese Sadi
Carnot, nel suo lavoro Réflexions sur la puissance motrice du feu […], del 1824 e può
essere così riassunta:
L’energia ricevuta per calore può essere restituita tramite lavoro, e quindi essere in
grado di spostare il punto di applicazione di una forza, unicamente per effetto
dei mutamenti che il calore può indurre nel volume e nella forma delle sostanze
a causa della dilatazione termica.
Per tale motivo trasferire energia attraverso il lavoro dopo averla ricevuta per
calore, è più facile se si sfruttano le sostanze aeriformi, per le quali il fenomeno
della dilatazione termica è in genere semplice da ottenere, ed è più consistente
che non nei liquidi o nei solidi.
Si può dire che per produrre lavoro il motore consuma del calore?
La generazione di lavoro non è riconducibile al “consumo" di calore, che in
quanto forma di energia non può in alcun caso essere distrutta. A produrre
lavoro è il passaggio di energia per calore da un corpo caldo ad uno freddo, allo
scopo di provocarne la dilatazione. E poiché si ha trasferimento per calore solo in
presenza di una differenza di temperatura, si può concludere che:
Per costruire un motore non è sufficiente trovare una sorgente da cui attingere
energia, ma occorre una differenza di temperatura
La produzione di lavoro può essere l’unico effetto del funzionamento di un motore?
Dato che il lavoro termodinamico di cui stiamo parlando, ottenuto dal
trasferimento di calore, è il risultato delle dilatazioni termiche, appare evidente
che una volta prodotto del lavoro il sistema che lo ha generato ha variato il suo
volume. Questo può essere enunciato formalmente dicendo che la produzione di
lavoro non è mai l’unico effetto della trasformazione di calore in lavoro.
Conseguentemente, se si vuole costruire un motore, si dovrà tenere anche conto
di tali effetti di variazione di volume. Altrimenti si avrà un motore che funzione
una sola volta, produce del lavoro ma poi non può essere sfruttato di nuovo, dato
che alla fine del processo esso non si trova più nelle condizioni di partenza. Si
pensi, ad esempio, al lavoro che si può produrre riscaldando un cilindro
contenente gas: il riscaldamento fa sollevare il pistone che produce così del
lavoro. Non è però pensabile di dilatare il gas illimitatamente, perché
praticamente si dovrebbe disporre di un cilindro di altezza infinita.
In termini pratici, quindi, di cosa ha bisogno un motore che sia efficiente?
Occorrerà che alla fine del processo di produzione del lavoro si riporti nelle
condizioni iniziali il sistema che si è dilatato. Tuttavia rimediare alle dilatazioni a
cui la trasformazione di calore in lavoro ha dato luogo significa compiere del
2
lavoro dall’esterno sul sistema, per comprimerlo nuovamente. Un altro modo
per dire la stessa cosa è che il motore termico, per funzionare, deve compiere una
trasformazione ciclica. Con il termine di ciclica si intende una trasformazione a
conclusione della quale lo stato di arrivo coincide con quello iniziale. A questo
punto il motore può ripartire e generare nuovo lavoro.
Allora dobbiamo far compiere al sistema esattamente gli stessi passi a ritroso?
Non è pensabile portare indietro il sistema ripercorrendo esattamente gli stessi
passi che esso ha fatto per produrre lavoro. Difatti, nel caso ideale di assenza di
dissipazioni, l’esatto percorso inverso richiederebbe da parte dell’ambiente lo
stesso lavoro che il sistema ha fornito nel dilatarsi.
Si pensi alla espansione isoterma reversibile di un gas perfetto che produce un
V
lavoro L nRT ln fin . Ricomprimere lo stesso gas isotermicamente, alla
Vin
medesima temperatura richiede che dall’esterno venga compiuto di nuovo sul
V
sistema un lavoro nRT ln in L .
Vfin
Questo è l’ esempio di un motore davvero pessimo, il quale riassorbe tutto ciò
che produce. La soluzione è piuttosto quella di riportare il sistema allo stato di
partenza seguendo un percorso differente dall’andata.
Come si sceglie il percorso per tornare allo stato iniziale?
Il criterio da usare è quello di rendere minimo il lavoro necessario, dato che nel
bilancio complessivo questo andrà sottratto al lavoro prodotto durante
l’espansione. Per appoggiare le idee, supponiamo che il sistema che fa da motore
sia un certo quantitativo di gas perfetto che segue trasformazioni reversibili e
quindi rappresentabili da curve sul piano di Clapeyron. Come sappiamo, più
bassa è la temperatura, più la linea che rappresenta la trasformazione si trova in
basso verso l’asse dei volumi, e quindi minore sarà il lavoro, cioè l’area sottesa1
fra due volumi qualunque. Se quindi il gas che in figura si sposta dallo stato 1
allo stato 2 producendo il lavoro LA , viene poi raffreddato fino allo stato 3 , il
processo di ritorno al volume iniziale richiede un lavoro LR minore di quello
da lui prodotto all’ andata. Come si deduce dal disegno, il ciclo sarà completo
solo se dopo si riporta anche la pressione al valore di partenza, riscaldando il gas.
Questo raffreddamento del motore può avvenire adiabaticamente, senza cedere calore?
Nell’esempio in figura il gas cede calore in due momenti, quando si raffredda da
2 a 3 e quando viene riportato al volume iniziale da 3 a 4 . Si può tentare di
ottenere lo stesso risultato immaginando che la prima delle due trasformazioni
sia adiabatica: possiamo raffreddare il gas senza che ceda calore, semplicemente
lasciandolo espandere ancora di più. Ma nella seconda, quando lo si vuole
riportare al volume iniziale, l’ambiente deve compiere lavoro sul gas, ed in
questa fase non possiamo evitare fuoriuscite di calore.
Si noti che questa identificazione del lavoro con l’area sottesa nel piano di Clapeyron perde di
significato nel caso di trasformazioni irreversibili
1
3
P
1
2
600 K
4
LA
500 K
3
LR
Vin
400 K
300 K
Vfin
V
Qualunque motore deve essere raffreddato?
La necessità di raffreddare i motori è del tutto generale e non riguarda solamente
l’espansione di un recipiente cilindrico ideale che contenga del gas perfetto.
Questo comporta il doversi sempre procurare una sorgente fredda alla quale
cedere calore. Si pensi al radiatore delle automobili, oppure ai grandi bacini
idrici in prossimità dei quali sono costruite le centrali termonucleari. Il
raffreddamento è indispensabile se vogliamo che il motore sia di utilità pratica:
P
Al termine del ciclo di un motore, il bilancio del lavoro deve essere positivo, deve
cioè essere prodotto più lavoro in espansione di quanto ne sia poi richiesto
durante la compressione.
Tmax
Tmin
Come si rappresenta un motore a gas perfetto nel piano P, V?
Durante il ciclo vi saranno in generale delle sorgenti dalle quali il motore assorbe
calore e sorgenti verso le quali lo cede. Se indichiamo con Tmax la temperatura
V della più calda delle sorgenti e con Tmin la più fredda di esse, i cicli operanti fra
P
ESPANSIONE
L>0
V
P
CONTRAZIONE
L<0
V
P
LAVORO
DEL CICLO
L>0
tali temperature estreme saranno compresi tra le isoterme reversibili di gas
perfetto corrispondenti. Se poi il motore a gas perfetto segue solo trasformazioni
reversibili possiamo anche raffigurare il suo percorso: trattandosi di un ciclo,
esso sarà costituito da una linea chiusa.
A cosa corrisponde nel piano P,V il lavoro di un ciclo di un motore reversibile?
Come sappiamo, il lavoro termodinamico compiuto durante le trasformazioni
reversibili è espresso dall’area sottesa dalle curve. Essa andrà presa con il segno
positivo oppure negativo a seconda del fatto che il volume aumenti o diminuisca,
cioè a seconda del fatto che la trasformazione proceda da sinistra verso destra nel
piano ( L 0 ) oppure da destra verso sinistra ( L 0 ).
Poiché in qualunque ciclo vi sarà una parte della trasformazione durante la quale
il sistema si espande, ed una parte in cui si ricontrae, il lavoro complessivo è alla
fine dato solo dall’area racchiusa entro il ciclo stesso. Il segno di L sarà positivo
se il gas si espande (reversibilmente) a temperature maggiori di quelle a cui si
ricontrae (il ciclo è percorso in verso orario), viceversa sarà negativo.
Come possiamo calcolare il lavoro compiuto durante un qualunque ciclo?
Si fa uso del primo principio della termodinamica. Dato che lo stato finale è
uguale a quello iniziale la variazione di energia interna in un ciclo deve essere
zero perché l’energia interna è una funzione di stato. Se quindi E int 0
avremo che alla fine del ciclo risulterà Q L . Il calore Q complessivamente
scambiato dal sistema sarà dato dalla somma di quello entrante, QC , ricevuto
dalle sorgenti calde, e di quello uscente, QF , ceduto alle sorgenti fredde. Ne
risulta che:
L Q QC QF QC | QF |
avendo esplicitato il segno del calore ceduto QF , sicuramente negativo.
V
4
Come si interpreta questo risultato?
La formula L QC | QF | può essere letta così: poiché devo raffreddare il
P
ESPANSIONE
sistema prima di poterlo riportare allo stato iniziale, non tutto il calore QC
QC
assorbito viene trasformato in lavoro.
Una parte di esso, QF , esprime l’energia spesa per raffreddare e ricomprimere il
sistema, e va necessariamente ceduto alle sorgenti a temperatura fredda con le
quali il motore deve essere in contatto, e quindi non viene convertito.
QF
CONTRAZIONE
Questo dà informazioni anche sull’efficienza del motore?
Quel che si può concludere è che il motore sarà tanto migliore quanto più QF
V
CICLO MOTORE
risulta piccolo. Infatti quanto più QF è piccolo tanto più grande è la porzione di
QC che viene trasformata in lavoro. Per quantificare la bontà di un motore si
introduce un parametro, detto rendimento, che si indica solitamente con la lettera
greca eta: . Il rendimento esprime numericamente quanto si è appena detto,
cioè quale frazione del calore assorbito viene trasformata in lavoro. L’espressione
matematica di è quindi il rapporto fra ciò che si è ricevuto dal motore, cioè il
Sorgenti calde
QC
L= QC-!QF!
lavoro L , e quello che si è dato al motore, cioè il calore QC :
lavoro prodotto
calore assorbito
Q | QF |
|Q |
L
C
1 F
QC
QC
QC
Come si vede risulta sempre 0 1 . Leggendo la frazione come quantitativo
del numeratore associato ad un’unità del denominatore, diremo che per ogni
Joule ricevuto in forma di calore, il rendimento esprime la frazione di esso che il
motore è in grado di restituire in forma di lavoro.
E’ possibile costruire un motore perfetto?
Un motore ideale trasformerebbe tutto il calore assorbito in lavoro. Il suo
rendimento sarebbe 1 . Ma abbiamo visto che non possiamo fare a meno di
cedere calore alla sorgente fredda. Quindi nessun motore può essere ideale.
Ci sono quindi due possibilità per un dispositivo che produca lavoro a partire dal
calore, sfruttando la dilatazione di un fluido. Se esso trasforma tutto il calore in
lavoro, non si tratta di un motore, perché ne risulterebbe uno stato finale diverso
da quello iniziale. Se invece lo stato finale coincide con quello iniziale allora il
dispositivo è un motore, perché ha compiuto un ciclo, tuttavia una parte del
calore risulta non utilizzata ai fini della trasformazione in lavoro, in quanto
ceduto alla sorgente fredda. Se ne può concludere che:
Per i motori reali risulta sempre un rendimento 1
5
M
QF
M
Sorgenti fredde
2. Il secondo principio della
termodinamica
La conclusione cui si è giunti sulle caratteristiche dei motori, venne espressa in
forma di principio fondamentale da parte del fisico britannico William Thomson
(poi divenuto Lord Kelvin, 1824 –1907):
Secondo Principio della termodinamica nella forma di Kelvin
Non esiste la macchina termica ideale, quella cioè che trasforma tutto il calore
assorbito da una sola sorgente in lavoro.
Trattandosi appunto di un principio, quanto esposto nel paragrafo precedente
non è la sua dimostrazione, ma solo una serie di ragionamenti (circoscritti fra
l’altro ai soli motori che seguono trasformazioni reversibili), volti a facilitarne la
comprensione. Il fatto che il motore ideale non esista è una legge della fisica, e
come tale frutto della sperimentazione ripetuta secondo il metodo galileiano. E
come per tutte le leggi della fisica, basterebbe anche un solo caso in cui essa non
valesse per falsificarla.
Quali legami ha il secondo principio con i fenomeni naturali del quotidiano?
Esiste una formulazione alternativa del secondo principio della termodinamica,
dovuta al fisico prussiano Rudolph Clausius (1822 -1888).
Invece dei problemi connessi con la realizzazione di una macchina termica,
Clausius prese in considerazione un fenomeno naturale apparentemente senza
alcuna relazione con quanto esposto fino ad ora: il verso di scorrimento del
calore.
Come si osserva quotidianamente, il rilascio spontaneo di energia per effetto
della differenza di temperatura ha una sola direzione: procede, infatti, da corpi a
temperatura superiore verso corpi a temperatura inferiore.
Il punto sul quale riflettere è che, sebbene sarebbe perfettamente compatibile con
il primo principio, un flusso spontaneo di calore da bassa verso alta temperatura
non ha mai luogo:
Il calore fluisce spontaneamente solo da corpi a temperatura superiore verso
corpi a temperatura inferiore
Si può realizzare uno spostamento di calore contro la direzione naturale?
Certamente si può, ma occorre una macchina frigorifera, una macchina, cioè, che
consumando energia trasferisce calore da oggetti freddi verso oggetti caldi.
Proprio come il frigorifero di casa: trasferisce calore dal cibo freddo (a bassa
temperatura) all’ambiente (a temperatura più alta) rendendo il cibo ancora più
freddo. Tutto questo, beninteso, consumando energia. Infatti i frigoriferi hanno
un spina connessa alla rete elettrica e se questa si stacca il trasferimento di calore
dal freddo al caldo cessa.
6
P
Come si rappresenta un frigorifero reversibile nel piano P, V?
Il principio di funzionamento del frigorifero è inverso a quello del motore: riceve
lavoro per sottrarre calore ad una o più sorgenti fredde e cederlo ad una o più
sorgenti calde. Anche la macchina frigorifera, per funzionare con continuità,
deve seguire una trasformazione ciclica che, nel caso in cui sia reversibile, può
essere raffigurata da una linea chiusa nel piano P,V.
CONTRAZIONE
QC
QF
ESPANSIONE
Come possiamo esprimere l’efficacia di una macchina frigorifera?
Un frigorifero funziona tanto meglio quanto più calore Qf riesce a prelevare
dalle sorgenti fredde a parità di lavoro L ricevuto. Trattandosi di un ciclo
avremo anche in questo caso Q L 0 , da cui L Q QC QF .
Il lavoro è subito dal frigorifero, quindi di segno negativo, così come è negativo il
calore uscente QC , mentre è positivo quello entrante QF . Esplicitando i segni si
ha L QC QF 0 cioè L QC QF .
La prestazione di un frigorifero viene allora espressa bene dal seguente rapporto
fra il calore prelevato ed il lavoro ricevuto:
k
QF
QF
calore prelevato
lavoro ricevuto
L
QC QF
Il rapporto k si dice efficienza, e rappresenta il numero di joule di calore che il
frigorifero può sottrarre alle sorgenti fredde per ognuno dei joule di lavoro
ricevuti.
Più grande è k , meno lavoro richiede la macchina per funzionare. Un frigorifero
ideale sottrarrebbe tutto il calore prelevato (cioè QC QF ) senza richiedere
lavoro esterno: per esso si avrebbe efficienza infinita. Ne concludiamo che
0 k .
Cosa mostrano le osservazioni riguardo al funzionamento del frigorifero ideale?
Il fatto che il trasferimento di calore da bassa ad alta temperatura non avvenga
spontaneamente, ma solo se si compie lavoro dall’esterno, ha delle conseguenze
sui limiti di funzionamento delle macchine frigorifere, riassunte da Clausius nel
modo che segue:
Secondo Principio della termodinamica formulato da Clausius:
Non esiste la macchina frigorifera ideale, cioè non è possibile effettuare una
trasformazione il cui unico risultato sia quello di trasferire calore da una
sorgente a temperatura inferiore ad una sorgente a temperatura più alta.
Come si interpreta per Clausius il funzionamento del frigorifero reale ?
L’enunciato di Clausius del secondo principio sostiene semplicemente che un
frigorifero non funziona senza attaccare la spina. Ovviamente ogni frigorifero
reale trasferisce calore da bassa ad alta temperatura, ma non è questo l’unico effetto
della sua azione. Il lavoro compiuto dall’esterno sul sistema comporta tutta una
serie di modificazioni ambientali, ad esempio quelle che ha prodotto la centrale
elettrica che ci fornisce l’energia necessaria affinché il frigo funzioni.
7
V
CICLO FRIGORIFERO
Sorgenti calde
QC
L= -!QC!+!QF!
QF
F
M
Sorgenti fredde
TC
QF
QC
A
B
QF
Il principio di Clausius esprime la stessa legge fisica di quello formulato da Kelvin?
La formulazione di Clausius è perfettamente equivalente a quella di Kelvin e
viceversa. Dimostriamo dapprima che se si può violare l’enunciato di Clausius
(tecnicamente diremo “se si può costruire una macchina anti-Clausius”), allora si
viola anche quello di Kelvin. In figura è schematizzato un motore termico A che
assorbe calore QC da una sorgente a temperatura calda TC e cede calore QF ad
una sorgente a temperatura fredda TF . Esso produrrà un lavoro L che, come si
L = QC- QF
è dedotto dal primo principio, sarà pari alla differenza fra il calore ricevuto e
QF
quello ceduto: L QC QF . Se ora disponessimo di una macchina B che
TF
violasse il postulato di Clausius potremmo usarla per riportare QF dalla
da anti-Clausius
ad anti-Kelvin
sorgente fredda a quella calda senza che sia necessario alcun apporto di lavoro
dall’esterno. La sorgente fredda sarebbe allora inutile: essa riceverebbe QF e poi
cederebbe di nuovo QF , ed è come se non avesse preso parte al processo. In
conclusione la macchina combinata A+B assorbirebbe calore solo dalla sorgente
a TC e produrrebbe il lavoro L QC QF , violando così il postulato di Kelvin.
TC
Q
B
L
A
Q
TF
da anti-Kelvin
ad anti-Clausius
E se si violasse il postulato di Kelvin, violeremmo Clausius ?
Se, viceversa disponessimo all’inizio di una macchina che violasse il postulato di
Kelvin (tecnicamente diremo “se si può costruire una macchina anti-Kelvin”),
indicata con la lettera B nella figura a lato, la potremmo utilizzare per estrarre
calore Q da una sorgente a temperatura TF e convertirlo integralmente in
lavoro L . Dato che non esistono limiti alla conversione di lavoro in calore (ad
esempio per attrito), potremmo prendere una macchina qualunque A che
ritrasformi il lavoro L in un calore avente caratteristiche di tali da poterlo
agevolmente trasferire ad una sorgente a temperatura TC TF . Per esempio
potremmo prendere come macchina A un dispositivo simile a quello di Joule che
metta in agitazione delle pale dentro ad un certo quantitativo di acqua ad una
opportuna temperatura. In conclusione la macchina combinata A+B assorbirebbe
calore da una sorgente fredda TF e lo trasferirebbe ad una sorgente calda TC
senza nessun altro effetto, violando così il postulato di Clausius. Si è dimostrato
quindi che se non esiste il motore ideale non esiste nemmeno il frigorifero senza
spina, e, viceversa, che se non esiste il frigorifero ideale non esiste nemmeno il
motore ideale.
Quali conseguenze ha avuto il secondo principio nello sviluppo della civiltà?
Il secondo principio della termodinamica costituisce un formidabile ostacolo con
il quale la civiltà umana ha dovuto confrontarsi. Mentre il calore è un processo di
facile realizzazione, in quanto è l’effetto del movimento caotico delle molecole
stesse, solo uno spostamento ordinato su scala macroscopica di miliardi di
molecole produce lavoro meccanico. La trasformazione di calore in lavoro è
essenziale per il progredire dell’intelligenza e delle strutture organizzate
socialmente. Qualche studioso sostiene che l’invenzione del motore a vapore,
avvenuta verso al fine del XVIII secolo, rappresentò il passo in avanti più
importante in assoluto della civiltà: grazie ad esso l’uomo si affrancò dalla
8
schiavitù dell’utilizzare la propria forza muscolare o quella animale e dalle
bizzarrie della natura. Ma il fatto che vi siano dei vincoli a tale conversione, in
particolare la necessità di utilizzare almeno due sorgenti a temperatura
differente, rende tutto il processo complicato. Sarebbe semplice produrre energia
elettrica (e quindi lavoro meccanico) se ad esempio si potesse estrarre calore dal
terreno. Riscalderemmo le nostre case diminuendo la temperatura dell’enorme
massa della crosta terrestre di così poco che nemmeno se ne potrebbe rivelare
l’effetto. Oppure se si potesse alimentare una nave risucchiando calore dal mare e
trasformandolo in lavoro. O ancora far correre un’auto o far volare un aereo
assorbendo calore dall’aria. Ma in tutti queste ipotesi fantasiose, il terreno, il
mare e l’aria rappresentano quella che nella nostra schematizzazione sarebbe la
sorgente calda. Nella pratica comune, invece, questi enormi bacini di calore si
utilizzano come sorgenti refrigeranti: ad essi i motori – anche quello delle auto cedono calore per raffreddarsi. Per estrarre calore dall’oceano necessiteremmo di
un altro oceano a temperatura più bassa: per ottenere da sorgenti termiche
energia in forma di lavoro, occorre disporre di una differenza di temperatura.
Può eseguire del lavoro un motore al quale non si fornisca energia?
Un motore deve compiere dei cicli, e ad ogni ciclo deve risultare E int 0 . In
conseguenza avremo che L Q , e quindi se Q 0 non possiamo sperare di
ricavare del lavoro da un simile meccanismo. Nel corso dei secoli molti sono stati
i tentativi di realizzare un motore che lavorasse senza somministrazione di
energia (ad esempio tramite un combustibile). I fallimenti puntualmente
registrati indicano chiaramente che l’energia non può essere creata, ma solo
convertita da una forma ad un’altra. Poiché una macchina capace di creare
energia potrebbe seguire dei cicli per un tempo indefinito, questa via di
conferma della validità del primo principio della termodinamica va sotto il nome
di impossibilità del moto perpetuo di prima specie.
Può eseguire del lavoro un motore che scambi calore con un’unica sorgente?
No, in quanto un simile dispositivo violerebbe il secondo principio della
termodinamica. Un ciclo che potesse alimentarsi traendo calore
dall’ambiente circostante, come ad esempio quello del motore di una nave
che estrae la sua energia dal solo oceano, avrebbe a disposizione una
sorgente di calore praticamente inesauribile, dando così vita ad un moto per
un tempo indefinito. Questo tipo di violazione del secondo principio è detta
impossibilità del moto perpetuo di seconda specie.
9
3. Il lavoro irreversibile
Come influiscono le irreversibilità sul rendimento di un motore?
Tutte le irreversibilità riducono il rendimento. Considerando ad esempio il
sistema semplificato costituito da un quantitativo di gas racchiuso entro un
cilindro dotato di stantuffo mobile, abbiamo che:
(1) Una trasformazione reversibile, allo scopo di evitare turbolenze, prevede
la situazione irreale in cui è possibile uno scambio di calore senza che vi
sia differenza di temperatura (o meglio in presenza di un T
infinitesimo) fra il sistema e la sorgente di calore. Se ipotizziamo che vi
siano irreversibilità dovute alla presenza di differenze di temperatura
fra sorgenti e sistema, poiché il calore scambiato aumenta proprio con
L
T , il rendimento
diminuisce perché è cresciuto il calore
QC
Pe
Pin
a
ricevuto QC
senza che a ciò corrisponda un maggiore esecuzione di
lavoro L sull’esterno.
(2) Se è la presenza di attrito a causare irreversibilità, questo impedisce che
tutto il lavoro eseguibile dal motore reale sia applicato all’ambiente: una
frazione di esso serve per vincere l’attrito, con la conseguente riduzione
del rendimento. Inoltre le parti meccaniche che subiscono attrito si
riscaldano e ne seguono rilasci irreversibili di calore verso l’esterno.
(3) Se avvengono altri processi rapidi e turbolenti, durante i quali non sono
definibili le variabili di stato, ed in particolare non lo è la pressione
interna, come vedremo nel seguito è sempre possibile trovare un
processo reversibile che, compatibilmente con lo stato del gas, svolga un
lavoro maggiore.
Cosa succede al pistone durante un’espansione irreversibile?
Poniamo che all’interno del gas vi sia una pressione Pi maggiore di quella
Pe che grava dall’esterno sul pistone (includendo in essa anche l’effetto del
suo peso), e che a mantenere fissa la parte mobile provveda un meccanismo
di blocco. Se si libera il blocco, poiché l’intensità della forza Fgas che il gas
esercita sul pistone verso l’alto supera l’intensità Pe A della forza che lo
spinge in basso il pistone si mette in moto con accelerazione verso l’alto
data da:
ma Fgas Pe A .
Quando la salita è molto brusca, gli strati di gas vicini al pistone divengono
più rarefatti rispetto a quelli prossimi al fondo. La pressione che esiste
all’interno è ora differente da quella che il gas esercita sulla superficie del
10
contenitore: per far coincidere i due valori lo stantuffo dovrebbe alzarsi con
velocità piccola rispetto a quella con cui la rarefazione si propaga nel gas
(cioè la velocità del suono). A meno che ciò non avvenga, durante
l’espansione non è più possibile definire un valore unico Pi per tutto il gas.
Se quindi la trasformazione non è reversibile siamo costretti ad usare le
“coordinate termodinamiche” dell’ambiente (in particolare il valore Pe della
pressione esterna) perché quelle del sistema non sono definite.
Quanto lavoro può complessivamente compiere il gas durante un’espansione?
Per ogni tratto di spostamento s , così piccolo da considerare la forza
costante, il lavoro elementare svolto sul pistone dalle due forze Fgas s e
Pe
s
Pfin
Pe As che agiscono su di esso è pari alla variazione della sua energia
cinetica Ec :
Fgas Pe A s Ec
ed introducendo la variazione di volume V As , ricaviamo che il
lavoro elementare Lgas Fgas s svolto dal gas sull’esterno vale:
Lgas Pe V Ec
In assenza del pistone, ad esempio per una razione chimica fra liquidi che
avviene alla pressione atmosferica, il ragionamento fatto si applica allo
strato di molecole d’aria immediatamente a contatto con le sostanze.
Pe Pi
Come possiamo sfruttare al massimo questo lavoro?
Dobbiamo osservare che la parte utile di lavoro è solo Pe V , cioè quella che il
gas esegue per contrastare la pressione esterna. E’ grazie ad essa che si
sollevano pesi e si muovono bielle, e quanto più è grande tanto meglio
stiamo facendo fruttare l’espansione. Viceversa il lavoro svolto per
incrementare l’energia cinetica del pistone è chiaramente sprecato ai fini
pratici. Per massimizzare il primo effetto e minimizzare il secondo, non
serve diminuire la massa del pistone, perché in tale caso esso andrà
semplicemente più veloce mantenendo invariata l’energia cinetica finale. La
soluzione è quella di ridurre la sua accelerazione aumentando la forza di
contrasto esterna Pe A fino al valore massimo consentito. Come si vede
l’accelerazione diverrebbe nulla se, aggiungendo pesi sul pistone si
arrivasse a Pe A Fgas , tuttavia non possiamo richiedere l’uguaglianza
esatta fra le due forze perché così si impedirebbe all’espansione di iniziare.
Quando però la pressione esterna diviene tale per cui Pe A è solo di
pochissimo inferiore a Fgas siamo vicini ad ottenere il massimo lavoro utile.
Ora il pistone si solleva con velocità molto bassa e praticamente costante. Se
queste condizioni sono verificate in ogni istante, la trasformazione è
reversibile ed il sistema rimane sempre in equilibrio termodinamico. E’
Fgas
quindi definibile anche la pressione interna, ed il suo valore è Pi
.
A
11
Pin
Pe Pi
s
Pfin
Possiamo immaginare di realizzare il processo asportando di volta in volta
dei granelli di sabbia posti sopra al coperchio in modo da mantenere sempre
verificata la condizione di reversibilità Pe Pi .
Come distinguiamo nel piano P-V il lavoro irreversibile da quello reversibile?
Quando il gas si espande bruscamente contro un valore costante di
pressione esterna Pe , partendo da un volume Vin fino ad unoVfin , il lavoro
irreversibile è l’area del rettangolo in verde in figura Lirr Pe (Vfin Vin ) . In
condizioni di reversibilità, invece, noti in ogni istante i valori della
temperatura e del volume del gas dobbiamo imporre alla pressione esterna
di assumere i valori forniti per la pressione interna dall’equazione di stato,
descritti dall’andamento della curva blu. Se pazientemente si segue questo
profilo, attraverso l’aggiunta o la rimozione dei granellini sabbia dal
coperchio, al lavoro irreversibile si aggiunge l’area in giallo, ed in queste
condizioni stiamo sfruttando al massimo il lavoro che il gas può compiere
sull’ambiente, compatibilmente con i suoi valori istantanei di temperatura e
di volume.
utilizzabile solo
se è reversibile
Pin Pe
Pfin Pe
Lirr Pe Vfin Vin
Pe
LA CONTROFISICA
Si faccia attenzione che quando sono
assegnati due stati termodinamici A e
B, non è detto che una trasformazione
reversibile fra A e B compia il lavoro
massimo: lo fa solo se il lavoro ha
sempre lo stesso segno durante la
trasformazione, cioè se il pistone si
sposta sempre nello stesso verso.
B
A
Vin
Vfin
Ci sono anche svantaggi nell’eseguire lavoro in condizioni di reversibilità?
A mano a mano che ci si avvicina alla condizione Pe Pi diminuisce la
velocità di espansione e, nel caso limite di perfetta reversibilità, il tempo
richiesto per l’espansione sarebbe infinito. Ad un processo così lento corrisponde
la minima potenza (cioè il minor quantitativo di lavoro svolto nell’unità di
tempo). Il lavoro reversibile è quindi un espediente per sondare le massime
possibilità teoriche delle macchine, ma non presenta vantaggi pratici.
12
4. Il motore di Carnot
Il rendimento di un motore non è mai 1 a causa delle irreversibilità?
Non è questa una formulazione soddisfacente del punto fondamentale. Dire che
i motori disperdono per irreversibilità (attriti, salti di temperatura, turbolenza)
significa che essi cedono calore alle sorgenti fredde che li circondano: aria,
acqua, od energia cinetica alle strutture dello stesso motore. I primissimi motori
termici, proprio a causa delle dispersioni, avevano un bassissimo rendimento.
Ad esempio la macchina a vapore dell’ingegnere inglese T. Newcomen (1705)
aveva 0.005 , così che il 99.95 % dell’energia andava sprecato. Un poco più
efficiente era quella dello scozzese J.Watt (1763), il quale, portando il meccanismo
di raffreddamento fuori dal motore, riuscì a far salire fino a 0.04 . Le
macchine attuali sono decisamente migliori, tuttavia anche una moderna
centrale nucleare non supera di molto 0.35 . Che è come dire che il 65 %
calore sprigionato dalle reazioni nucleari se ne va a riscaldare i pesci del lago.
Quanto è ampio il margine di miglioramento nel rendimento di un motore?
Si potrebbe pensare che con idee ingegnose che eliminassero tutti gli attriti, le
turbolenze e le irreversibilità in genere, insieme al raffinamento dei meccanismi,
potremmo sperare di costruire la macchina perfetta, che restituisca integralmente
in forma di lavoro l’energia ricevuta come calore. Ma questa possibilità è nella
pratica negata, poiché fra le cause che abbassano il rendimento di un motore vi è
quella intrinseca, ineliminabile, legata alle inesorabili conseguenze del secondo
principio della termodinamica, che prevede in ogni caso la cessione di un certo
quantitativo di calore ad una sorgente fredda. Per indagare in questa direzione
lo scienziato francese Sadi Carnot (1796 –1832), nella sua opera Riflessioni sulla
potenza motrice del fuoco, (1824) fece uso di alcune astrazioni per isolare il
problema principale. Il suo punto di arrivo fu di ricavare il rendimento del
miglior motore che si possa immaginare: quello che oggi viene denominato il
“ciclo di Carnot”.
Quali sono le caratteristiche di un motore ideale secondo Carnot?
Come si è visto, il fatto che durante una trasformazione reale un aeriforme non
attraversi solo stati di equilibrio, ma, in generale, in un punto esso avrà una
temperatura e un poco più a destra una temperatura diversa, in una zona una
certa pressione e più a sinistra una pressione differente, comporta un’esecuzione
di lavoro inferiore a quello massimo ottenibile in quelle condizioni. Il primo dei
miglioramenti di Carnot rispetto ai processi reali fu di limitarsi alle
trasformazioni reversibili, cioè successioni di stati di equilibrio e con l’assenza di
qualunque attrito. Tuttavia questa non è l’unica semplificazione possibile, perché
se vogliamo un motore che funzioni rispettando il secondo principio della
termodinamica, non si può fare a meno di cedere calore, oltre che riceverlo. In
particolare la formulazione di Kelvin stabilisce che il motore che scambia calore
con una sorgente sola non può funzionare. Carnot pensò allora alla cosa più
semplice dopo il motore – impossibile - ad una sola sorgente: il motore che
13
CICLO
DI CARNOT
DUE SOLE
TRASFORMAZIONI
SORGENTI
REVERSIBILI
scambia calore con due sole sorgenti. Due ma non più di due: una calda ed una
fredda.
P
Ma in linea di principio quante sorgenti può avere un motore reversibile?
Supponiamo di avere un gas perfetto che compie un ciclo reversibile compreso
fra due isoterme, una alla temperatura di 300 K e l’altra a 400 K . Chiedersi
400K
300K
V
qual è il numero di sorgenti con cui il gas scambia calore durante il ciclo è come
domandarsi quante isoterme sono comprese fra quella a temperatura massima e
quella a temperatura minima. In effetti sono possibili un numero infinito di tali
trasformazioni, proprio come infiniti sono i numeri reali compresi fra 300 e 400 .
E dato che le trasformazioni seguite non sono adiabatiche, il sistema deve
scambiare calore durante tutto il tragitto e deve scambiarlo mentre varia la sua
temperatura. E se vogliamo che gli scambi di calore siano reversibili anche la
temperatura della sorgente deve variare, perché, lo si è visto, uno scambio di
calore fra oggetti a temperatura diversa comporta irreversibilità. Il sistema deve
quindi necessariamente interagire con infinite sorgenti a temperatura diversa.
Anche nella realtà le sorgenti di calore sono infinite?
Con il termine sorgente intendiamo un’astrazione, un sistema immaginario la cui
temperatura si mantiene uniforme e costante nonostante gli scambi di calore. In
molte applicazioni, il terreno, l’aria atmosferica, l’acqua di un fiume o del mare
possono essere assimilati a sorgenti. Nella realtà si hanno motori che scambiano
calore con tre, quattro sorgenti. Ma per uno scambio reversibile di calore è
indispensabile che non vi siano differenze di temperatura tra sistema e sorgenti:
se quindi sono infinite le temperature che il sistema attraversa, infinite debbono
di necessità essere anche le sorgenti di scambio. Nel caso irreversibile è
indifferente parlare di temperatura del sistema o di temperatura della sorgente.
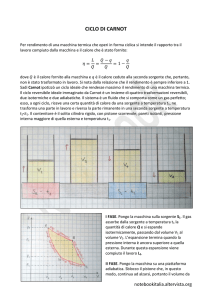
V2 V3
V1 V2
V3 V4
TC
Espansione isoterma: il gas
riceve calore alla temperatura
TC e compie lavoro
V4 V1
TF
Raffreddamento adiabatico: il
gas compie lavoro a spese della
propria energia interna
Compressione isoterma: il
gas subisce lavoro e cede
calore alla temperatura
14
TF
Riscaldamento adiabatico: il
gas subisce lavoro a vantaggio
della propria energia interna
Come possiamo schematizzare la prima fase di questo semplice motore ideale?
Assumiamo quindi due sole sorgenti di scambio, una calda ed una fredda. Vi
sarà una fase iniziale durante la quale il motore produce lavoro ricevendo calore
dalla sorgente calda a temperatura TC . La sostanza che compie il ciclo all’interno
del motore dovrà dilatarsi ma, al tempo stesso, rimanere a temperatura costante.
Se infatti la sua temperatura variasse, dovendo essere il sistema in equilibrio con
la sorgente per avere uno scambio reversibile di calore, sarebbe necessario
mutare anche la temperatura di quest’ultima. Come risultato comparirebbero
nuove sorgenti con cui interagire, una per ogni salto di temperatura. La fase di
assorbimento di calore e generazione di lavoro
deve pertanto essere
un’espansione isoterma.
Cosa succede dopo che il motore ha compiuto lavoro?
Il sistema va ora raffreddato fino alla temperatura TF della sorgente fredda.
L’unico modo per passare da TC a TF senza che avvengano scambi di calore,
(che richiederebbero ulteriori sorgenti a temperature intermedie), è attraverso
un’espansione adiabatica.
Nella fase successiva è l’ambiente a compiere lavoro sul sistema?
Adesso che il sistema è alla temperatura TF devo ricomprimerlo per riportarlo al
volume iniziale, quindi dobbiamo lavorare su di esso dall’esterno. Valgono
ancora le considerazioni fatte sopra: per avere scambi reversibili di calore il
lavoro necessario a ridurre il volume deve essere eseguito mantenendo il sistema
a temperatura costante: la trasformazione è ancora un’isoterma ma questa volta
in compressione.
Affinché il sistema si ritrovi nelle condizioni di partenza ora va riscaldato?
Sì, per chiudere il ciclo è necessario riportare il fluido alla temperatura TC , ma
questo senza ulteriori scambi di calore, altrimenti occorrerebbero ancora delle
sorgenti intermedie ulteriori. L’unica via percorribile è quella di una
compressione adiabatica.
Il ciclo di Carnot è dunque un ciclo motore reversibile a due sole sorgenti,
costituito da due isoterme e due adiabatiche
Qual è il fluido che compie il ciclo?
Non vi sono indicazioni circa la natura del fluido impiegato: qualunque sostanza
che svolga reversibilmente un ciclo di due isoterme e due adiabatiche sta
seguendo un ciclo di Carnot. Solo allo scopo di calcolare il rendimento,
possiamo supporre che si tratti di un gas perfetto. In questo caso è anche nota la
rappresentazione del motore sul piano di Clapeyron, che rappresentiamo nella
figura successiva. Resterà poi da capire cosa accade variando la natura della
sostanza.
15
1
2
TC
4
TF
3
V
I L MOTORE DI CARNOT A GAS PE RFETTO
Quanto Q ed L scambia un motore a gas perfetto che compie un ciclo di Carnot?
Nel piano di Clapeyron il gas si trova inizialmente nello stato di equilibrio 1, e da
qui si espande reversibilmente, in una prima fase mantenendo costante la sua
temperatura fino a che non raggiunge lo stato 2, in una seconda fase senza
scambiare calore, lungo l’adiabatica che lo conduce allo stato 3.
Successivamente viene compresso, sempre reversibilmente, prima di nuovo a
temperatura costante fino allo stato 4, poi ancora in modo adiabatico fino a
ritornare nello stato iniziale 1.
Una sorgente calda a temperatura TC deve fornire al gas il calore necessario a
mantenere isoterma l’espansione 1 2. Ricordiamo che in un gas perfetto,
durante ogni isotema anche l’energia interna rimane costante, cioè E int 0 .
Allora possiamo applicare il primo principio, ottenendo che tutto il calore QC
assorbito dal gas viene sfruttato per l’esecuzione di lavoro nella fase 1 2 :
QC L12 nRTC ln
V2
V1
Poiché lungo l’adiabatica 23 non avviene scambio di calore, al lavoro L23 che
viene compiuto dal gas sull’ambiente deve corrispondere un calo nel serbatoio
dell’energia interna, al quale il gas attinge per espandersi, e quindi abbiamo una
diminuzione della temperatura.
Durante l’isoterma 3 4 viene compiuto lavoro sul gas, e se vogliamo che questo
non vada ad incrementare il livello del serbatoio di energia interna elevando così
la temperatura, deve esserci una sorgente fredda TF ad impedire il riscaldamento.
Il calore QF che esce dal gas è, in valore assoluto, uguale al lavoro L34
negativo che il gas esegue:
QF L34 nRTF ln
essendo infatti
V4
V3
nRTF ln
V4
V
1 risulta ln 4 0 , da cui:
V3
V3
ln
V4
V
V
ln 4 ln 3 .
V3
V3
V4
16
V3
V4
.
L’ultima fase 41 prevede che il gas, che diminuisce in volume senza scambiare
calore, si riscaldi di nuovo fino alla temperatura iniziale. A questo processo il
primo principio fa corrispondere un aumento di energia interna uguale, in
valore assoluto, al lavoro negativo compiuto dal gas.
V
Al termine del ciclo , il gas avrà dunque assorbito calore QC nRTC ln V2 ad
1
alta temperatura e ne avrà ceduto
una parte
QF nRTF ln
V3
V4
a bassa
temperatura. In base al primo principio il lavoro compiuto sarà pari alla
differenza fra i due calori: L QC QF .
Quanto vale il rendimento di un motore di Carnot a gas perfetto?
Il rendimento di un motore dipende dal rapporto fra i calori scambiati:
QF
1
. In base a quanto detto, per un ciclo di Carnot si trova:
QC
| QF |
QC
| L34 |
L12
nRTF ln
nRTC ln
V3
V4
V2
.
V1
Ora abbiamo che lungo la
trasformazione adiabatica 2 3 risulta
1
1
TCV2 TFV3 , e durante l’adiabatica 4 1 è invece TCV1 1 TFV4 1 . Se
queste due relazioni vengono divise membro a membro, si ha:
TC V21
TC V11
TF V31
TF V41
V2 V3
.
V1 V4
Sostituendo questa relazione in quella che dà il rapporto fra i calori scambiati si
semplificano i due logaritmi a numeratore e denominatore:
| QF | TF
.
QC
TC
Ne deriva che, nel caso di un gas perfetto, il rendimento di un ciclo di Carnot
risulta:
C 1
TF
TC
Cosa dice questo risultato sulle proprietà del rendimento di un ciclo di Carnot?
Abbiamo dimostrato che quando un gas perfetto esegue un ciclo di Carnot il
rendimento dipende solo dalla temperatura delle due sorgenti. La posizione che
hanno, sulle isoterme nel piano di Clapeyron, i vertici del ciclo, indica solamente
17
LA CONTROFISICA
Potrei mettere nella mia auto un motore di
Carnot?
Sarebbe del tutto sconsigliabile: si tratta di
un dispositivo ideale, privo di qualsiasi
utilità pratica. Non potremmo mai
realizzare isoterme ed adiabatiche
reversibili, ma anche se ci riuscissimo il
processo di ingresso ed uscita del calore
sarebbero così lenti che otterremmo
macchina certamente molto economica,
ma che non supererebbe la velocità di
una lumaca. Detto diversamente, sarebbe
bassissima la potenza erogata, visto che il
lavoro prodotto, pur essendo il massimo
possibile, viene reso disponibile in un
tempo molto lungo.
quanto grande stiamo costruendo il motore, cioè quanto lavoro L QC QF il
P
CICLI DI CARNOT A GAS PERFETTO
CHE FANNO USO DI DIFFERENTI
QUANTITÀ DI GAS
MA HANNO UGUALE
RENDIMENTO
TC
TF
V
ciclo può fornirci, ma non dà informazioni sulla sua efficacia, cioè sulla relazione
fra L ed il calore assorbito QC . Inoltre quanto più la temperatura TF della
sorgente fredda diventa piccola rispetto alla temperatura TC della sorgente
calda, tanto più il rendimento cresce. Se TF fosse zero Kelvin, il rendimento
assumerebbe il suo valore ideale pari ad 1 e tutto il calore assorbito dalla
sorgente calda verrebbe restituito in forma in lavoro.
Quel è invece l’efficienza di un ciclo frigorifero di Carnot?
Per un ciclo frigorifero di Carnot, cioè una macchina ideale che, tramite
trasformazioni reversibili, sottrae calore ad un’unica sorgente fredda per cederlo
ad un’unica sorgente calda, si trova, facendo uso della relazione
kC
QF
QC QF
QF
TF
QC
1
QF
QC
18
TC
TF
1T
C
TF
TC TF
| QF |
QC
TF
TC
:
5. Un “supercarburante” per il motore di
Carnot
Se a compiere il ciclo di Carnot non è un gas perfetto, il rendimento cambia ?
Abbiamo calcolato il rendimento del motore di Carnot nel caso specifico in cui a
compiere il ciclo di due isoterme e due adiabatiche sia un gas perfetto, ottenendo
T
C 1 F , un risultato indipendente dalle posizioni dei vertici del ciclo (dove
TC
si incontrano adiabatiche ed isoterme), cioè indipendente dalle quantità di calore
scambiate. Vogliamo ora dimostrare che se a compiere il ciclo di Carnot è una
qualunque altra sostanza, ad esempio un gas reale, oppure una miscela di più
gas, come l’aria, un insieme di gas e vapori, o altro ancora, il rendimento rimane
lo stesso:
Tutti i cicli reversibile che scambiano calore solo con due sorgenti, una a
TC ed una a TF , sono detti cicli di Carnot, ed il loro rendimento è sempre
1
TF
TC
qualunque sia il sistema fisico che compie il ciclo.
TC
Ma fissate T C e T F , cosa può ancora variare nel motore di Carnot a gas perfetto?
Supponiamo di avere un motore di Carnot a gas perfetto, C A , che operi fra
100 J
due sorgenti a TC ed aTF , ed il suo rendimento, fissato dalle temperature,
1
sia, ad esempio, A . Osserviamo che si può ottenere A costruendo un
5
motore della dimensione che vogliamo: quello in figura preleva QC 100 J e
80
1
. Ma il
100
5
rendimento sarebbe lo stesso se il motore fosse più grande (e lavorasse
quindi con un maggior quantitativo di gas), ad esempio prelevando
QC 150 J , producendo L 30 J e cedendo QF 120 J . Anche in questo
produce L 20 J cedendo QF 80 J : risultato A 1
caso avremmo A 1
CA
20 J
80 J
TF
120
1
.
150
5
Cosa rispondere a qualcuno che sostenesse di poter superare il nostro motore?
Poniamo che qualcuno si presenti sostenendo di aver scoperto un super
carburante. Utilizzandolo per alimentare il suo motore di Carnot C B , egli è
convinto di poter battere il rendimento del nostro a gas perfetto, pur
lavorando fra le stesse temperature. In formule dovremmo dire che per
assurdo si sta ipotizzando l’esistenza di un C B con B A . Assumiamo
TC
100 J
CB
dunque che il motore C B faccia fruttare molto meglio del nostro il calore
QC 100 J prelevato dalla sorgente calda, trasformandone in lavoro una
parte più consistente, diciamo L 40 J e che di conseguenza sia più piccola
60 J
l’energia rimanente che viene ceduta alla sorgente fredda sotto forma di
TF
19
40 J
calore, cioè QF 100 40 60 J . Il rendimento sarebbe in questo caso
60
2
. Ma come si è visto, anche se il
100
5
rendimento è fissato, possiamo fare il nostro C A grande come vogliamo.
esattamente il doppio: B 1
Tariamolo allora in modo che produca anche lui gli stessi 40 J di lavoro. Per fare
questo, siccome è per ipotesi meno efficiente, pretenderà di ricevere
maggior calore dalla sorgente calda rispetto a C B , nello specifico servono
QC 200 J , e ne cederà di più alla sorgente fredda: QF 160 J . In questo
modo infatti si ha L QC QF 200 160 40 J .
TC
100 J
200 J
E facendo questo si mette in difficoltà il motore sfidante?
Per porre in difficoltà C B sfruttiamo la reversibilità del motore di Carnot e
facciamo funzionare il nostro C A al contrario. C A diventa una macchina
frigorifera che, ricevendo 40 J di lavoro, è in grado di prelevare 160 J dalla
CA
40 J
160 J
60 J
TF
CB
sorgente fredda e di spostarli in quella calda. Ora chiediamo al padrone di
C B di fornirci lui i 40 J di lavoro necessari per far funzionare il frigorifero.
Possiamo stare certi di aver smascherato l’impostore perché se davvero fosse
possibile alimentare C A in questo modo avremmo costruito un frigorifero
senza spina. Guardiamo infatti l’azione combinata delle due macchine
racchiuse entro la linea tratteggiataC A C B . Dalla sorgente fredda esce un
calore che complessivamente vale 160 J 60 J 100 J , e lo stesso
quantitativo entra nella sorgente calda: 200 J 100 J 100 J . Il dispositivo
combinato C A C B sarebbe allora una macchina che, senza ricevere lavoro
dall’esterno, può spostare calore da una temperatura bassa ad una più
elevata, in piena violazione del postulato di Clausius.
Ma questa dimostrazione numerica ha una validità generale?
Quanto detto non è limitato dal fatto che si sono scelti particolari valori.
Quali che siano il rendimento ed il lavoro prodotto, è sempre possibile
ripetere il ragionamento contro chiunque sostenesse di poter fare meglio di
un motore di Carnot fra due temperature fissate: è sufficiente ingrandire il
nostro motore finché non arriva a fornire lo stesso lavoro del suo, quindi
trasformarlo in un frigorifero e poi chiedere a lui di alimentarlo.
Possiamo concludere che i due rendimenti sono uguali?
Dai ragionamenti sopra si conclude soltanto che non può essere vera l’ipotesi che
B A . Deve allora valere per forza la relazione ad essa complementare, e cioè
che: B A . A questo punto potremmo ripetere l’intero ragionamento
scambiando i ruoli di C A e di C B : partendo dall’ipotesi A B e facendo
adesso funzionare a rovescio C B si ottiene che non può essere nemmeno vero
che A B e che quindi varrà la sua complementare, cioè A B . Dovendo
essere vero sia B A sia A B , l’unico modo in cui ciò può avvenire è
che:
20
A B
e quindi abbiamo dimostrato tutti i cicli di Carnot che lavorano fra le medesime
temperature hanno lo stesso rendimento, indipendentemente dalla sostanza che
adoperano.
E se la macchina B non fosse reversibile?
Se poi la macchina B non è una macchina di Carnot, ma una qualunque
macchina irreversibile a due sorgenti allora varrà solo la prima metà della
dimostrazione, non essendo ora più possibile invertire il funzionamento di una
macchina irreversibile semplicemente cambiando di segno alle quantità di calore.
Pertanto risulta dimostrato anche che per una macchina qualunque, che scambia
calore con due sole sorgenti, il rendimento è Carnot e se la seconda macchina è
anch’essa di Carnot vale il segno di uguaglianza.
Esempio 1
Nelle centrali nucleari si produce la scissione dei nuclei atomici, che sprigiona
frammenti dei nuclei di Uranio dotati di grande energia cinetica. Questi
frammenti veloci sono usati per riscaldare acqua, formando vapore che
raggiunge una temperatura di 533 K . Si consideri dunque un impianto che ha
un rendimento 0.330 , ed è costruito nelle prossimità di un fiume, che per la
sua temperatura media 286 K è sfruttato per il raffreddamento. Dovremmo
incolpare gli ingegneri di aver progettato un macchinario altamente inefficiente?
In questa centrale solo un terzo dell’energia della fissione dell’uranio viene
convertita in energia elettrica, tuttavia un impianto di Carnot che lavorasse fra le
stesse due temperature avrebbe un rendimento:
T
286
C 1 F 1
0.463
TC
533
Questo valore rappresenta un limite superiore per il rendimento di qualsiasi
centrale nucleare a fissione si voglia costruire nei pressi di quel fiume. E
considerati gli inevitabili attriti che riducono il rendimento ideale, ci pare che
ottenendo 0.330 gli ingegneri abbiano svolto un lavoro egregio.
Esempio 2
Una macchina termica produce in ogni ciclo un lavoro L 100 J scambiando
calore con due sole sorgenti a TC 500 K e TF 300 K . Sapendo che il suo
rendimento è 0.250 si dica se la macchina è reversibile, e si trovino i calori
scambiati con ciascuna sorgente.
Se la macchina fosse reversibile, avendo due sole sorgenti di scambio il suo
rendimento sarebbe quello di un motore di Carnot che opera fra le stesse due
temperature:
21
LA CONTROFISICA
Tutti i motori reversibili hanno lo stesso
rendimento di quello di Carnot?
No, per uguagliare il ciclo di Carnot un
motore, anche se reversibile, deve
scambiare calore con due sole sorgenti,
altrimenti ne
esce inesorabilmente
sconfitto.
C 1
TF
TC
1
300 2
0.400
500 5
La macchina è quindi irreversibile essendo 0.250 0.400 . Per il calcolo dei
calori scambiati dalla formula per il rendimento si ha:
L
100
100
0.250
QC
400 J
QC
QC
0.250
E dal primo principio:
L QC QF
QF 400 J 100 J 300 J
Esempio 3
Stimare la minima quantità di lavoro necessaria ad un frigorifero per trasformare
in gelato a 4.00°C un chilogrammo di latte che si trova alla temperatura
ambiente di 35.0°C . Si assumano per il latte tutte le caratteristiche dell’acqua, in
particolare il calore specifico c 4186 J / Kg K ed il calore latente di
fusione/solidificazione 3.34 105 J/K
Calcoliamo il calore da sottrarre al latte per ottenere il gelato: esso si compone di
tre contributi. Innanzitutto abbiamo il calore Q1 da sottrarre per portare il latte
alla temperatura di solidificazione 273 K
Q1 mc(0 35) 1.00 4186 35 1.47 104 J
poi c’è il calore Q2 da sottrarre per solidificare il latte:
Q2 m 3.34 105 1.00 33.4 104 J
ed infine il calore Q3 per portare la temperatura a 4 C :
Q3 mc(4 0) 1.00 4186 4 0.167 104 J
per un totale di:
Q 1.47 104 J 33.4 104 J 0.167 104 J 35.0 104 J
Il minimo lavoro necessario per sottrarre al latte questo calore è quello svolto da
un ciclo frigorifero di Carnot che lavori fra le due temperature :
TF 4 273 268 K e TC 35 273 308 K .
La sua efficienza vale:
TF
k
29.8
TC TF
che è pari anche al rapporto
QF
, cioè il frigorifero di Carnot può sottrarre al
L
latte 29.8 J di calore con ogni Joule di lavoro ricevuto. Da questo risulta che il
lavoro minimo per fare il gelato vale:
L
35.0 104 J
29.8
1.17 104 J
22
Esempio 4
Sulla base dei principi della termodinamica, si dica se le macchine illustrate a lato
sono dei dispositivi che possono realmente funzionare.
Il dispositivo A è un motore che non può esistere perché, pur rispettando il
primo principio:
L QC QF 50 J 10 J 40 J
viola apertamente il secondo, dato che il suo rendimento supera quello di una
macchina di Carnot che lavori fra le stesse temperature.
T
L
40 4
400 1
C 1 F 1
QC
50 5
TC
600 3
Il dispositivo B è un frigorifero possibile, che rispetta sia il primo principio:
L QC QF 50 J 10 J 40 J
Il dispositivo C non è né un motore né un frigorifero: preleva calore da due
sorgenti a temperatura diversa e lo converte in lavoro. Questo apparecchio
rispetta il primo principio, poiché il calore entrante equivale al lavoro prodotto:
L 20 J 40 J 60 J
ma non può esistere perché così tutto il calore prelevato dalla sorgente a 600 K
sarebbe trasformato in lavoro, ed analogamente diverrebbe lavoro tutto il calore
prelevato dalla sorgente a 300 K , in aperta violazione della formulazione di
Kelvin del secondo principio.
Esempio 5
Un condizionatore da 750 W è in grado di raffreddare al ritmo di 5000 BTU
( 1 BTU 1055 J ) all’ora. Si valuti la sua efficienza in relazione a quella di un
frigorifero ideale che debba mantenere una temperatura interna di 20.0 °C
quando all’esterno si hanno 30.0 °C .
In un’ora viene sottratto alla stanza il calore QF 5000 1055 5.275 106 J ,
questo
grazie al
lavoro
L 750 Wh ,
che,
trasformato in
Joule
risulta L 750 W 3600 s/h 2.700 106 J .
L’efficienza del condizionatore vale: k
QF
L
5.275 106 J
2.700 106 J
1.954 , mentre
per un frigorifero ideale che lavori fra TF 293 K e TC 303 K si avrebbe:
k
TF
TC TF
293
29.3
303 293
23
600 K
50 J
A
50 J
B
40 J
10 J
40 J
10 J
300 K
300 K
600 K
40 J
C
sia il secondo, essendo la sua efficienza inferiore a quella di una macchina
frigorifera di Carnot che lavori fra le stesse temperature:
QF
TF
300
3
10
1
kC
k
40
4
T
T
600
200
4
L
C
F
e
600 K
60 J
20 J
300 K
6. La temperatura termodinamica
Possiamo usare il ciclo di Carnot come termometro?
Come sappiamo, i termometri a mercurio, o che in genere fanno uso di liquidi,
presentano disaccordo a causa dei differenti coefficienti di dilatazione. Quelli a
gas (perfetto) mostrano maggiore omogeneità, però non sono più utilizzabili alle
bassissime temperature, quando il gas reale condensa. Un ciclo di Carnot,
invece, può essere svolto da una qualunque sostanza, anche in fase condensata.
Poiché il suo rendimento è indipendente dal fluido utilizzato, e legato solo alle
temperature, possiamo allora trasformare il ciclo di Carnot in un termometro . Si
sceglie una temperatura di riferimento, quella del punto triplo dell’acqua, e si
assegna ad essa il valore misurato con la scala termometrica a gas perfetto:
Ttriplo 273.16 K . Fatto questo possiamo stabilire qual è la temperatura di un
corpo semplicemente misurando il rapporto fra i calori scambiati da una
qualunque sostanza che svolga un ciclo di Carnot fra la temperatura di
riferimento Ttriplo 273.16 K , e la temperatura T dell’oggetto:
T
Ttriplo
Q
Qtriplo
Q
T 273.16
Qtriplo
La temperatura così introdotta, che è in sostanza una misura di calore, si dice
temperatura termodinamica del corpo. I suoi valori coincidono con quelli della
scala Kelvin già introdotta tramite il gas perfetto, ovviamente solo nella regione
in cui questa si può materialmente misurare.
T
Q1
C
L
Q2
C
L
Q3
Perché esiste uno zero per la temperatura termodinamica?
Supponiamo di avere una sorgente a temperatura T da cui venga prelevato
calore Q1 ad opera del primo di una serie di cicli di Carnot, posti in modo che il
calore ogni volta uscente venga immesso nel ciclo successivo. Se ognuno dei
cicli esegue lo stesso lavoro L , a ciascun passo deve corrispondere un calore in
uscita sempre minore, e nel contempo il quantitativo complessivo Q1 va
progressivamente ad esaurirsi. Prima o poi dovremo giungere ad un ultimo
passo in cui, per produrre lo stesso lavoro L , tutto il calore entrante viene
utilizzato e niente è ceduto. La temperatura così prodotta dai motori è ritenuta di
zero assoluto: scendere al di sotto richiederebbe un rendimento maggiore di 1 cioè
più lavoro in uscita che non calore in ingresso, violando il primo principio.
QN
C
L
E’ possibile raggiungere lo zero della scala della temperatura termodinamica?
Il secondo principio della termodinamica vieta espressamente la possibilità
1 in quanto implicherebbe QF 0 , ossia potremmo fare a meno della
sorgente fredda. Ora, nel motore di Carnot si ha 1 quando TF 0 K , e
dunque dobbiamo concludere che non è mai possibile non solo scendere sotto a
0 K , ma nemmeno raffreddare la materia fino ad un tale valore di temperatura.
24
7. Il teorema di Clausius
Consideriamo un sistema A che compia una trasformazione ciclica. Durante la
trasformazione, in generale
A scambierà calore, reversibilmente od
irreversibilmente, con un certo numero di sorgenti, T1,T2 , Tn .
Q
Consideriamo il rapporto i fra il calore Qi scambiato con ciascuna di esse
Ti
A
T1
T2
…
…
Tn
…
Tn
e la temperatura della sorgente stessa. Vogliamo valutare il segno della
Q
somma di questo rapporti, cioè il segno di: i . Non conoscendo né il
Ti
valore dei calori né il loro verso di scambio, e neanche le temperature delle
sorgenti, non appare evidente se una tale quantità debba essere positiva,
negativa oppure nulla. Tuttavia un risultato dovuto a Clausius mostra che:
in una trasformazione ciclica, cioè che alla fine del processo riporta tutte le
funzioni di stato al valore iniziale, la somma dei rapporti
Qi
Ti
non può mai
essere positiva.
Come si può giungere ad una tale conclusione ?
Immaginiamo delle macchine di Carnot C 1 , C 2 , C n , che lavorino fra le
temperature Ti e la temperatura di una sorgente esterna T0 . Supporremo
che durante ogni ciclo, ciascuna di esse scambi con le T1 , T2 , Tn gli stessi
calori (ma in verso opposto), che queste sorgenti scambiano con A .
Questo è possibile sebbene il rendimento di Carnot sia fissato dalle temperature?
Sebbene il rendimento della macchina sia fisso, la dimensione può essere
scelta a piacimento. Possiamo costruirla grande in modo da farle produrre il
lavoro che vogliamo, ma anche della dimensione giusta per farle scambiare
il quantitativo di calore che desideriamo. Se quindi Qi è uscito dalla
sorgente Ti per entrare in A , costruiremo la macchina C i della dimensione
necessaria affinché ceda a Ti la stessa quantità Qi . Se viceversa è Ti ad
aver acquistato calore da A , faremo C i abbastanza grande affinché glielo
sottragga nuovamente tutto.
In un ciclo quanto calore viene complessivamente scambiato con la sorgente T0 ?
Consideriamo un ciclo del nuovo sistema composto dall’unione di A con
C 1 , C 2 , C n : esso scambia calore unicamente con la sorgente T0 .
Ovviamente non sappiamo se nel complesso il calore sia entrato od uscito
da T0 . Chiamiamo Q0 il suo valore e diciamo L0 il lavoro prodotto dalle
macchine. Come accade al termine di un ciclo, anche qui non sarà mutato il
contenuto energetico interno: E int 0 , e dal primo principio segue che
Q0 L0 0 . Quindi tutto il calore scambiato deve uguagliare il lavoro
prodotto: Q0 L0 .
25
A
T1
T2
C1
C2
…
Cn
T0
Ma così non si sta violando il secondo principio nella forma di Kelvin?
Un sistema come questo, che riceve calore da una sola sorgente, non può
avere come unico risultato la sua trasformazione integrale in lavoro. L’unica
possibilità di evitare la contraddizione col postulato di Kelvin è che il
sistema non stia ricevendo dalla sorgente T0 il calore Q0 per tramutarlo in
lavoro L0 , ma che avvenga piuttosto il viceversa. Dobbiamo cioè concludere
che, grazie al lavoro
L0 , il calore Q0 viene ceduto alla sorgente T0 dal
sistema composto A C 1 C 2 C n . E poiché un calore uscente dal
sistema ha segno negativo si ha:
Q0 0 .
Abbiamo mostrato che Q0 è negativo , ma come possiamo ricavare il suo valore ?
Indicando con Q0i il calore che ciascuna macchina scambia con la sorgente
T0 , sfruttando le proprietà dei cicli di Carnot risulta per ognuno
Q0i
T
Q
0 , da cui Q0i T0 i . Sommando i vari Q0i si ha Q0 :
Qi
Ti
Ti
Q0
Q
Q0i T0 Tii
0
e poiché T0 è espressa in Kelvin e non può essere negativa, si conclude che :
Q
Tii
0
relazione nota come disuguaglianza di Clausius.
E se la trasformazione ciclica di A fosse anche reversibile?
Il sistema A potrebbe seguire lo stesso ciclo al contrario. Chiamando Qi* i
nuovi calori scambiati, il ragionamento fatto per giungere alla
disuguaglianza di Clausius continuerebbe a valere, cioè dovrebbe ancora
essere Q0 0 per non violare il postulato di Kelvin, da cui, come prima
Q*
deduciamo Q0 T0 Ti 0 . Ma percorrendo al contrario un ciclo
i
reversibile, i calori hanno solo mutato il verso di scorrimento, e quindi
risultaQi* Qi , che inserita nella
Q*
Ti
i
Qi*
T
0 produce:
i
Qi
Ora si deve osservare che le due relazioni
essere contemporaneamente vere solo se:
26
Ti
0
Q
Tii
Q
Tii
0 e
0 possono
Q
Tii
0
risultato che va sotto il nome di teorema di Clausius, e che mostra come il
segno di uguale nella precedente disuguaglianza di Clausius si trova solo
quando le trasformazioni sono reversibili. Per il teorema di Clausius, al
posto della sommatoria si fa di solito uso di un simbolo più compatto, la
somma integrale su un percorso chiuso reversibile
:
rev
rev
dQ
0
T
dove si considera il caso più generale in cui invece di avere un numero di
sole n temperature di scambio, la temperatura T delle sorgente vari con
continuità durante il ciclo, assumendo infiniti valori diversi. Il ciclo viene
allora ad essere costituito da un numero infinito di scambi di quantitativi
microscopici di calore dQ (da leggere de-Q) ciascuno ad una sua T .
Quale proprietà corrisponde al teorema di Clausius?
Esso estende la proprietà
dei cicli di Carnot,
| QF | TF
, (e cioè
QC
TC
P
QC
Q
F 0 ) ad ciclo reversibile con più di due sorgenti. Ciò significa
TC
TF
che è sempre possibile una scomposizione di un ciclo reversibile in tanti
tratti di isoterma ed adiabatica, cioè è lecita un’approssimazione tramite cicli
di Carnot. La figura illustra il caso particolare del ciclo di un gas perfetto,
sovrapposto ad un insieme di cicli di Carnot a gas perfetto anch’essi, aventi
temperature di poco differenti fra di loro. L’approssimazione può essere resa
tanto migliore quanto più fitta si fa la suddivisione.
Se il ciclo è reversibile cosa indicano le temperature nella sommatoria ?
Uno scambio reversibile di calore deve avvenire senza differenze di
temperatura. Quindi nella disuguaglianza di Clausius, oltre a valere il segno
di uguale, i valori delle temperature delle sorgenti al denominatore sono in
realtà uguali a quelle del sistema.
Come possiamo enunciare a parole queste due relazioni dovute a Clausius?
Se al termine di un ciclo irreversibile di un sistema che scambia calore con
n sorgenti, si fa la somma dei rapporti fra i calori scambiati e le temperature
delle sorgenti di scambio, si ottiene sempre un numero negativo. Se il ciclo è
invece reversibile, tale somma vale zero, ed inoltre le temperature da
riportare nella sommatoria coincidono con quelle assunte dal sistema
durante il ciclo.
27
V
8. Il teorema di Carnot
Si è già visto già per i cicli irreversibili a due sole sorgenti si ha: Carnot . E’
tempo ora che il ciclo di Carnot si misuri con motori a più di due sorgenti,
reversibili od irreversibili che siano. In generale, anche se le sorgenti sono in
numero infinito, si potrà sempre individuare quella con la più alta temperatura,
Tmax , e quella con la temperatura più bassa, Tmin . Diremo allora che il motore
P
sta operando fra Tmin e
Tmax
Tmin
V
Tmax . Un caso particolare
è quello di un ciclo
reversibile, ad infinite sorgenti, compiuto da un gas perfetto: la sua
rappresentazione sul piano di Clapeyron è compresa fra le isoterme
corrispondenti alle due temperature estreme.
Evidenzieremo ora in modo inequivocabile la schiacciante superiorità del
motore di Carnot rispetto a qualunque concorrente, dimostrando che nessun
motore può avere un rendimento superiore al suo:
Teorema di Carnot: il massimo rendimento fra tutti
i cicli termici che
operano fra la stessa temperatura minima Tmin e massima Tmax compete ai
cicli reversibili che scambiano calore solo con due sorgenti, una a Tmin ed
una a Tmax . Essi sono detti cicli di Carnot, ed il loro rendimento è sempre
1
Tmin
Tmax
qualunque sia la natura del sistema fisico che compie il ciclo.
Quanto vale il rendimento di un ciclo con più di due sorgenti?
Durante il ciclo vi saranno momenti durante i quali entra calore nel sistema e
momenti in cui ne esce. Indicando i primi con QE ed i secondi con QU , in
base alla definizione di rendimento avremo:
1
| QU |
| QE |
Cosa dice la disuguaglianza di Clausius riguardo ad un ciclo a più sorgenti ?
La disuguaglianza di Clausius assicura che per i cicli con un numero
Q
qualunque di sorgenti si ha i 0 , dove il segno di uguale vale solo nel
Ti
particolare caso di ciclo reversibile. Distinguendo i calori entranti ed uscenti,
ed introducendo i moduli per esplicitare il segno, riscriviamo la
disuguaglianza nella forma:
| QE |
TE
28
| QU |
0.
TU
Possiamo far figurare le temperature massima e minima in queste sommatorie?
Se ora i calori QE della prima sommatoria, invece che per le temperature
delle sorgenti dalle quali entrano, li dividiamo per Tmax otteniamo un
addendo più piccolo:
| QE |
|Q |
E .
Tmax
TE
Allo stesso modo, se nella seconda sommatoria dividiamo i calori QU per
Tmin , stiamo sottraendo un numero maggiore di prima:
|Q |
U
Tmin
| QU |
.
TU
Il risultato di queste due sostituzioni è di diminuire il valore di tutta
l’espressione, che quindi diviene strettamente negativa:
|Q |
|Q |
E
U
Tmax
Tmin
0
Possiamo portare le temperature massima minima fuori dalla sommatoria?
Essendo due valori costanti, possiamo certamente raccogliere Tmin e Tmax
fuori dalla sommatoria, per cui
QE
Tmax
QU
Tmin
0 , e quindi riscrivere:
| QU | Tmin
| QE | Tmax
E se inseriamo il risultato trovato nella formula per il rendimento del motore?
T
Se al posto del rapporto fra i calori sottraiamo la quantità più piccola min
Tmax
otteniamo un numero più grande:
1
| QU | 1 Tmin
Tmax
| QE |
Carnot
Quest’ultima relazione mostra che il rendimento di un qualunque ciclo
reversibile, è minore di quello di un ciclo di Carnot che scambia calore solo con
sorgenti alle temperature massima e minima fra cui il ciclo sta lavorando2.
2
Per i cicli irreversibili si può invece mostrate che il rendimento non è mai maggiore di quello di Carnot.
29