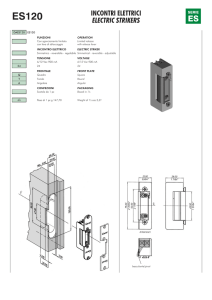
Descrizione del Ponte di Wheatstone
Nello schema, Rx rappresenta la resistenza di valore incognito da misurare; Rn , R1 e R2 sono tre resistenze: Rn è detta
resistenza di taratura, mentre R1 ed R2 sono due resistenze di valore variabile. Tra A e C, mediante un generatore,
si applica la tensione d’alimentazione. Tra B e D si inserisce un galvanometro, ovvero uno strumento che permette
di misurare il valore della corrente elettrica che lo attraversa. La condizione che consente di misurare il valore di Rx
è quella in cui il ponte sia in equilibrio, cioè la condizione in cui non vi sia passaggio di corrente tra B e D: questo
avviene nel momento in cui il potenziale elettrico del punto B è uguale a quello del punto D, e questa condizione si
ottiene variando opportunamente i valori delle resistenze R1 e R2 .
Quanto il ponte è in equilibrio, la corrente che attraversa Rx , ix , è uguale a quella che attraversa Rn , mentre la
corrente che passa attraverso R1 , i12 è la stessa che scorre attraverso R2 ; se si chiama VAC il valore della differenza di
potenziale tra il punto A ed i punto C, allora si ha che:
ix =
VAC
,
Rx + Rn
i12 =
VAC
R1 + R2
Visto che, quando il ponte è in equilibrio, il potenziale del punto B è uguale a quello del punto D, si deve avere che
VAB sia uguale a VAD ; utilizzando la prima legge di Ohm si ha:
VAB = Rx ix = Rx
VAC
,
Rx + Rn
da cui si ricava che
Rx
VAD = i12 R1 = R1
VAC
R1 + R2
VAC
VAC
= R1
Rx + Rn
R1 + R2
Semplificando VAC e prendendo il reciproco di entrambi i membri, si ottiene che:
Rn
R2
=
Rx
R1
da cui si ricava
Rx =
R1
Rn
R2