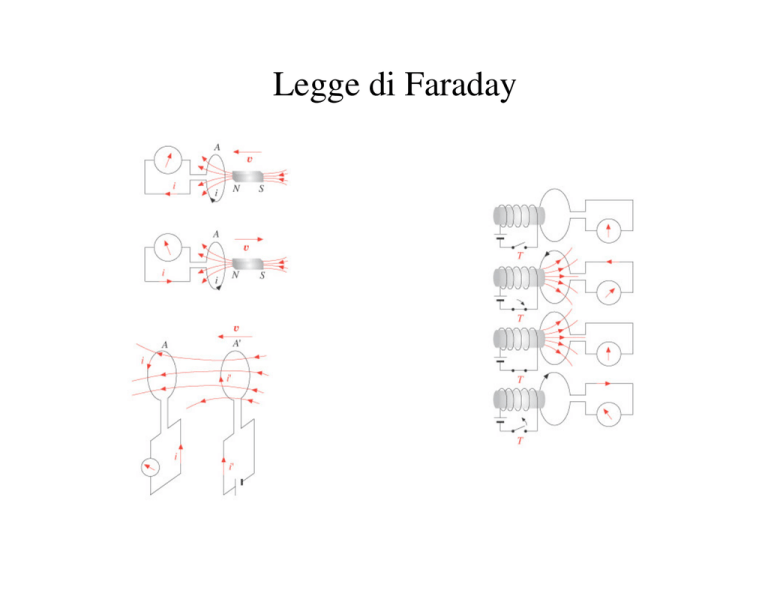
Legge di Faraday
Legge di Faraday
dΦ ( B )
fi = −
dt
Se R è la resistenza del circuito
fi
1 dΦ ( B )
i= =−
R
R dt
Ricordando che la forza elettromotrice è
per definizione
dΦ ( B )
f i = Ei • ds = −
dt
La variazione del flusso magnetico
concatenato con una linea chiusa s da
origine ad un campo elettrico indotto non
conservativo
La legge di Faraday si può anche scrivere
dΦ (B )
d
B • un dΣ =
fi = −
=−
dt
dt Σ
d
B cosθdΣ =
−
dt Σ
1) Si può variare B
2) Si può variare l’angolo
3) Si può deformare il circuito
Legge di Lenz
La f.e.m. indotta in un circuito ha
sempre verso tale da produrre una
corrente che tende ad opporsi alla causa
che lo ha generato
L’unità di flusso magnetico è il Weber
(Wb)
In un circuito ha luogo la variazione
di 1 Wb quando questa variazione, in
un secondo, provoca una fem di 1 V.
∂
f i = Ei • ds = −
B • un dΣ =
∂t Σ
F
Ei =
=v×B
−e
N
f i = v × B • ds = v × B • ds = −vBb
M
Φ( B ) = B • un dΣ = Bbx
∂Φ
∂x
fi = −
= − Bb = −vBb
∂t
∂t
N
f i = v × B • ds = v × B • ds = −vBb
M
Attrito elettromagnetico
f i = −vBb
vBb
i=−
r+R
2 2
Bb
F = ib × B = −
v
r+R
Resistenza di attrito elettromagnetico
2 2 2
Bbv
2
P = Fext • v =
= (r + R )i = fii
r+R
La potenza meccanica impiegata, viene
ritrovata integralmente sotto forma di
potenza elettrica spesa sulle resistenze del
circuito
Generatore di corrente alternata
Φ( B ) = B • un dΣ = BΣ cosθ = BΣ cos ωt
dΦ (B )
fi = −
= ωBΣsenωt
dt
f max = ωBΣ
Se la spira è collegata ad una R
f i ωB Σ
i= =
senωt
R
R
P = Ri =
2
(ωBΣ )
2
R
sen ωt
2
Valor medio della potenza
Pm =
(ωBΣ )
2
2R
f max
=
2R
2
Il generatore di c.a. è equivalente ad un
generatore di c.c. la cui f.e.m. detta efficace è
f eff
f max
=
2
Correnti di Foucault
Legge di Felici
1 Φ2
Φ1 − Φ 2
q = i (t )dt = −
dΦ =
t1
R Φ1
R
t2
Il valore della carica non dipende dalle
legge temporale con cui varia il flusso
Autoflusso
µ0 ds × ur
B=
i
2
4π
r
Φ (B ) =
µ0 ds × ur
i
•
u
d
Σ
n
2
4π
r
Φ (B ) = Li
L si chiama coefficiente di autoinduzione
o induttanza
L’induttanza di un circuito misura il
flusso del campo magnetico concatenato
con quel circuito quando attraversato
da una corrente di intensità unitaria
Un circuito ha un’induttanza di un henry
se, una corrente di un ampere che fluisca
in quel circuito, concatena con esso un
flusso di induzione di un weber
Quando in un circuito la corrente non è
costante nel tempo, il flusso concatenato
varia e nel circuito compare una f.e.m.
indotta
dΦ (B )
di
fL = −
= −L
dt
dt
Un circuito con induttanza non nulla si dice
induttivo
induttore
dΦ (B )
di
fL = −
= −L
dt
dt
>0
Circuito RL
f + f L = Ri
di
f = L + Ri
dt
di
dt
R
= → ln( f − Ri ) = − t + cos t
f − Ri L
L
f − Ri = Ae
− Rt L
Chiusura del circuito
t=0 i=0
A=f
f
−t τ
i (t ) = (1 − e )
R
L
τ=
di
−t τ
R
f L = − L = − fe
dt
Chiusura del circuito
f −t τ
fL
i∞ − i(t ) = e = − = iL
R
R
quindi
i (t ) = i∞ − iL
Extracorrente di chiusura
Apertura del circuito
f −t τ '
i (t ) = (e )
R
L
τ '=
R'
di
R ' −t τ '
f L = − L = − fe
dt
R
fL
= iL = i (t )
R'
Energia magnetica
di
2
fi = Li + Ri
dt
fidt = Lidi + Ri dt
2
Lavoro compiuto
dal generatore
Lavoro speso
contro la f.e.m. di
autoinduzione
Bilancio energetico
Effetto joule
Lavoro speso contro fL nel tempo in cui la
corrente passa dal valore zero al valore i
1 2
W = Lidi = Li
0
2
i
Possiamo definire la energia intrinseca
della corrente
1 2
U L = Li
2
Nel passaggio da zero a i∞
1 2
U L = Li∞
2
Durante l’apertura del circuito la corrente
torna a zero e nel resistore viene speso il
lavoro
f −t τ '
i (t ) = (e )
R
L
τ '=
R'
2
∞
f
2
R'
i dt = R ' 2
0
R
∞
0
e
t L
−2 R '
1 2
dt = Li∞
2
Leghiamo l’energia al campo magnetico,
localizzandola nello spazio in cui esiste
un campo magnetico
Consideriamo un tratto di lunghezza d di un
solenoide indefinito
2
2
1 2 1
B
B
2
2
U L = Li = (µ0 n Σd )i =
Σd =
τ
2
2
2 µ0
2 µ0
La densità di energia risulta
2
B
um =
2 µ0
Densità di energia magnetica
In un volume τ intorno ad un punto P in cui
il campo magnetico vale B
2
B
dU m = um dτ =
dτ
2 µ0
2
B
Um =
dτ
τ 2 µ0
Capacità di un condensatore piano
σ
E = un
ε0
σ
q
V1 − V2 = Eh = h =
h
ε0
ε 0Σ
q
ε 0Σ
C=
=
V1 − V2
h
Ue di un condensatore piano
CV
1 ε 0Σ 2 2
Ue =
=
E h
2
2 h
1
1
2
2
= ε 0 E Σh = ε 0 E τ
2
2
2
Densità di Ue
Ue
1
2
ue =
= ε0E
τ 2
In una regione dello spazio in cui è definito
un campo elettrostatico l’energia contenuta in
un volume infinitesimo, al cui interno il
campo valga E, è
1
2
dU e = ε 0 E dτ
2
Energia totale del campo elettrostatico
1
2
U e = dU e = ε 0 E dτ
τ2
Questa energia corrisponde al lavoro speso
per costruire la distribuzione di cariche che
dà origine al campo
1
2
U e = ε 0 E dτ
τ2
2
B
Um =
dτ
τ 2 µ0
Induzione mutua
Φ1, 2 (B1 ) = B1 • un dΣ 2
Φ 2,1 (B2 ) = B2 • un dΣ1
Φ1, 2 (B1 ) = M 1, 2i1
Φ 2,1 (B2 ) = M 2,1i2
In base alla legge di Faraday si ha una
f.e.m. indotta in un circuito dalla
variazione di corrente dell’altro
dΦ 2,1
di2
f1 '
=−
= − M 2,1
dt
dt
dΦ1, 2
di1
f2 '
=−
= − M 1, 2
dt
dt
Considerazioni energetiche
Portiamo i1 a regime, i2 =0
1 2
U1 = Li1
2
Considerazioni energetiche
Portiamo i2 a regime, i1 =cost
1 2
U 2 = Li2
2
di2
U 2,1 = − f1 '
i1dt = M 2,1 i1dt =M 2,1i1i2
dt
Considerazioni energetiche
In totale il lavoro speso dai generatori
trasformato in energia legata alla presenza del
campo magnetico è:
1 2 1 2
Li1 + Li2 + M 2,1i1i2
2
2
Considerazioni energetiche
In totale il lavoro speso dai generatori
trasformato in energia legata alla presenza del
campo magnetico con procedimento inverso è:
1 2 1 2
Li1 + Li2 + M 1, 2i1i2
2
2
Considerazioni energetiche
Poiché i due stati finali sono uguali ciò implica:
M 1, 2 = M 2,1
Due circuiti per i quali M≠0 si dicono
accoppiati, M si definisce induttanza
mutua e si misura in H
Energia magnetica di due circuiti accoppiati
1 2 1 2
U m = Li1 + Li2 + Mi1i2
2
2
Corrente di spostamento
dq d (CV )
is =
=
=
dt
dt
d ΣV
d
dΦ (E )
= ε0
= ε 0 (ΣE ) = ε 0
dt h
dt
dt
B • ds = µ 0 i =
= µ 0 j • u n dΣ
Σ
Equazione di continuità
Conservazione della carica sotto forma differenziale
q(t ) = ρdτ
τ
dq(t ) d
∂ρ
=
ρdτ =
dτ
τ ∂t
dt
dt τ
La variazione della carica nell’unità di tempo per la
conservazione della carica deve uguagliare la carica che
nello stesso dt ha attraversato la superficie S che racchiude
quel volume
Σ
∂ρ
j • un dΣ = −
dτ
τ ∂t
Per il teorema della divergenza
Σ
j • un dΣ = ∇ • j dτ
τ
∂ρ
∇• j +
=0
∂t
∇• j = 0
Condizione di stazionarietà
∂ρ
∇• j +
=0
∂t
1
∇•E = ρ
ε0
∂E
∂E
js = ε 0
∇ • j + ε0
=0
∂t
∂t
∇ • ( j + js ) = 0
Il vettore j + js è solenoidale
∇ × B = µ0 j
diventa ∇ × B = µ0 ( j + js )
In forma integrale
B • ds = ∇ × B • un dΣ =
Σ
µ0 j • un dΣ +µ0 js • un dΣ =
Σ
Σ
∂Φ (E )
∂
µ0 i + ε 0
E • un dΣ = µ0 i + ε 0
∂t
∂t Σ
Legge di Faraday
Un campo magnetico variabile crea un campo elettrico.
dΦ (B )
E • ds = −
dt
L’integrale è esteso ad una qualunque linea chiusa e Φ(B) è il
flusso d’induzione concatenato con quella linea.
∂B
∇× E = −
∂t
Legge di Faraday
dΦ ( B )
E • ds = −
dt
∂B
∇× E = −
∂t
Hanno validità generale; esse sona valide anche quando il campo
elettrico è creato sia da campi magnetici variabili che da cariche
elettriche; infatti in tal caso il campo elettrico è dato da
E = Es + Ei
∇ × Es = 0
∂B
∇ × Ei = −
∂t
Legge di Ampere-Maxwell
Una corrente elettrica, sia essa di conduzione o di spostamento,
crea un campo magnetico; o anche un campo elettrico variabile
crea un campo magnetico
dΦ ( E )
B • ds = µ 0 i + ε 0
=
l
dt
µ0
( j + j s ) • u n dΣ
Σ
Ove js è la densità di corrente di spostamento, l una qualunque
linea chiusa ed Σ una qualunque superficie avente per contorno
quella linea
Legge di Ampere-Maxwell
∇ × B = µ 0 ( j + js )
∂E
js = ε 0
∂t
Legge di Gauss
Fornisce la relazione tra il campo elettrostatico e le cariche che
lo creano.
E • un dΣ =
q
∇•E =
ε0
1
ε0
ρ
Queste relazioni, sebbene stabilite in elettrostatica hanno
validità generale: sono valide anche quando il campo è creato
sia da cariche elettriche che da campi magnetici variabili infatti
in tal caso il campo elettrico è dato da:
E = Es + Ei
Legge di Gauss
E = Es + Ei
∇ • Es =
1
ε0
ρ
∇ • Ei = 0
Solenoidalità del vettore B
B • u n dΣ = 0
∇•B = 0
Equazioni di Maxwell
E • un dΣ =
q
ε0
B • u n dΣ = 0
dΦ (B )
E •ds = −
dt
dΦ ( E )
B •ds = µ0 i + ε 0
dt












