Classificazione dei Moti
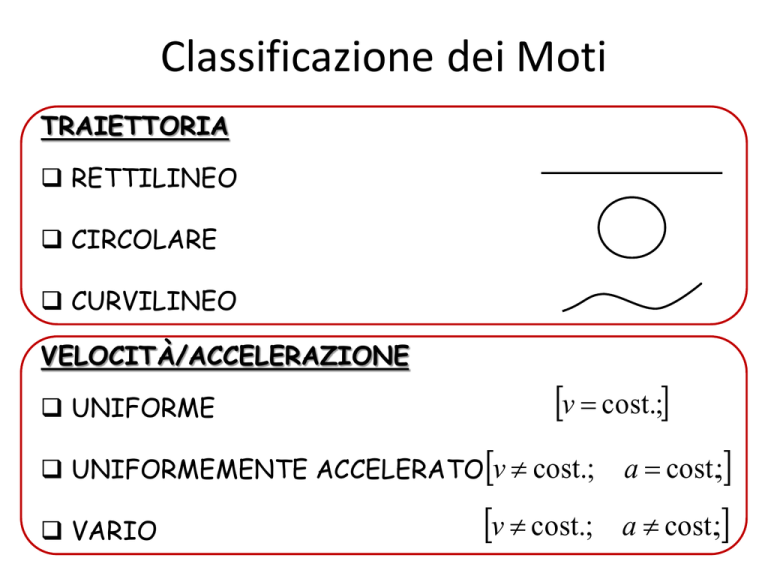
TRAIETTORIA
RETTILINEO
CIRCOLARE
CURVILINEO
VELOCITÀ/ACCELERAZIONE
UNIFORME
v cost.;
UNIFORMEMENTE ACCELERATO v cost.;
a cost.;
v cost.;
a cost.;
VARIO
Moto Rettilineo Uniforme
Un moto si definisce RETTILINEO UNIFORME se sono
verificate le seguenti condizioni:
La traiettoria è una retta
La velocità è costante (e quindi l’accelerazione è
nulla).
La legge oraria, cioè l’equazione matematica che lega
spazio e tempo, del moto rettilineo uniforme è:
s s0 v t
Moto Rettilineo
Uniformemente Accelerato
Un moto si definisce RETTILINEO UNIFORMEMENTE
ACCELERATO se sono verificate le seguenti condizioni:
La traiettoria è una retta
L’accelerazione è costante
La legge oraria, cioè l’equazione matematica che lega
spazio e tempo, del moto rettilineo uniformemente
accelerato è:
1
2
s s0 v0 t a t
2
v v0 a t
Moto di Caduta libera dei corpi
Un caso particolarmente interessante di moto rettilineo
uniformemente accelerato è la caduta libera dei corpi
attratti dalla forza di gravità (forza peso).
La caduta libera fu studiata da Galileo Galilei, lo
scienziato pisano mostrò che i corpi materiali cadono,
nel vuoto (escludendo quindi qualunque effetto
di attrito), tutti con la stessa accelerazione,
indipendentemente dalla loro massa.
L’accelerazione costante con cui i corpi cadono è
l’accelerazione di gravità g = 9,8m/s2.
Moto Circolare Uniforme
Un moto si definisce CIRCOLARE UNIFORME se sono
verificate le seguenti condizioni:
La traiettoria è una circonferenza
La velocità è costante in modulo
Nel moto circolare uniforme si ha inoltre che:
VELOCITÀ TANGENZIALE: v = 2pr/T
il vettore velocità è costante in modulo ed è in ogni
istante tangente alla circonferenza.
ACCELERAZIONE CENTRIPETA: a = v2/r
il vettore accelerazione è non nullo, costante in modulo
ed è in ogni istante diretto verso il centro della
circonferenza.
Moto Armonico
Si definisce MOTO ARMONICO il moto oscillatorio
compiuto dalla proiezione di un punto che si muove lungo
una circonferenza a velocità costante, cioè di moto
circolare uniforme, sul diametro della circonferenza.
La velocità è massima al
centro, quando passa per il
centro, e minima (uguale a
zero) negli estremi, quando
il moto si inverte.
Poiché la velocità non è
costante il moto non è
uniforme ma accelerato.
Mentre il punto P si sposta lungo l’arco di circonferenza da A verso
B, la sua proiezione Q si sposta lungo il diametro da A verso B.
il moto non è uniforme ma accelerato
– la velocità è massima al centro del diametro e
minima (nulla) agli estremi (dove il moto si inverte)
la durata di un’oscillazione completa è il periodo del
moto armonico
il numero di oscillazioni complete compiute in un
secondo è la frequenza
la velocità angolare è la pulsazione
s
La legge oraria del moto armonico
La posizione angolare del punto P in funzione del tempo e
della velocità angolare è espressa dalla relazione
=t
Indicando con r l’ampiezza massima dell’oscillazione e
con la pulsazione, la legge oraria del moto armonico
è
L’accelerazione nel moto armonico
L’accelerazione nel moto armonico è data in generale dalla
relazione
a = -2 s
Quindi, l’accelerazione
è direttamente proporzionale al quadrato della
pulsazione
è sempre diretta in verso opposto allo spostamento s
dalla posizione centrale
è massima quando lo spostamento s è massimo
è nulla quando il corpo si trova al centro
Il moto armonico
Il grafico della funzione coseno
Il grafico della funzione coseno sul piano cartesiano è una
curva detta cosinusoide
anche la rappresentazione grafica della legge oraria del
moto armonico è una cosinusoide











