s_151125

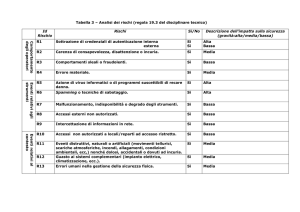
STATISTICA E CALCOLO DELLE PROB.
Mercoledì 25 novembre 2015
Prof. Cesare Svelto
Tempo a disposizione 2 ore (30+25+20+20+25)
1° Appello (1a P.I.) AA 2015/2016
Aula V.S.7 ore 13.15
Cognome e nome: ___________________________________ _____________________
Matricola e firma __ __ __ __ __ __
(stampatello)
_____________________(firma leggibile)
Esercizi svolti (almeno parzialmente): 1 2 3 4 5 (7+7+6+6+7 = 33p)
(crocettare)
N.B. Per consegnare il compito occorre svolgere, almeno parzialmente, tutti gli esercizi. Si richiede di
crocettare tutti gli esercizi e sottopunti, tipo 1a) 1b) 1c) 1d) 1e), almeno parzialmente svolti. Compiti
consegnati e corretti, poi risultati gravemente insufficienti comporteranno il “salto di un appello”.
SOLUZIONI
Esercizio 1 (tempo stimato 30 minuti)
(svolgere su questo foglio e sul retro)
1)
Al termine di un corso di subacquea i 12 allievi svolgono una prova di immersione in apnea, riportando
i seguenti risultati di profondità raggiunta:
H = X [m] = 11.5 9.6 11.3 10.8 12.2 8.9 11.1 10.9 10.1 9.3 11.4 14.5
1a)
Dopo avere riportato le formule descrittive, si calcolino media e varianza delle profondità nel campione
considerato, spiegando l’utilità di queste statistiche.
1b)
Si riportino i dati sul foglio di probabilità gaussiana nel quale l’asse delle ordinate è stato riscalato da
valori P (probabilità) a valori z (variabile normale standard). Si commenti il risultato ottenuto,
motivando i ragionamenti svolti e le regole e convenzioni seguite.
1c)
Si costruisca un diagramma rami e foglie dai dati misurati.
1d)
Si disegni l’istogramma della frequenza cumulativa, sia assoluta che relativa, dei dati.
1e)
Si dia la definizione di percentile, si calcoli il 40-esimo percentile e si rappresenti il box-plot dei dati,
unitamente ai punti sperimentali (dot-plot), riportando i calcoli svolti per ottenerne i valori significativi.
2.51a) Secondo
la loro definizione, a partire dai dati del campione possiamo calcolare:

media campionaria = x 
1 n
 xi  10.97 m
n i 1
n

varianza campionaria = s 2 
(x  x)
i 1
2
i
n 1
 2.21 m2
La media campionaria è uno stimatore non polarizzato del valor medio della popolazione che si sta
campionando. Si può dimostrare che è uno stimatore più efficiente che non il singolo campione, in quanto
presenta un errore quadratico medio inferiore.
La varianza campionaria è uno stimatore non polarizzato della varianza della popolazione. È una
misura del grado di dispersione della popolazione attorno alla media.
_______
Pag. 1/11
2.51b) Gli
j
xj
*
F (xj)=P
n=12 dati ordinati e la corrispondente distribuzione cumulativa osservata, F*(xj)=(j-0.5)/n, sono:
1
2
3
4
5
6
7
8
9
10
11
12
8.9
9.3
9.6
10.1
10.8
10.9
11.1
11.3
11.4
11.5
12.2
14.5
4.2% 12.5% 20.8% 29.2% 37.5% 45.8% 54.2% 62.5% 70.8% 79.2% 87.5% 95.8%
Dai valori P di probabilità osservata sperimentalmente si possono ricavare i corrispondenti valori z per una
VNS, andando a leggere in tabella di (z) della gaussiana standard in corrispondenza di P il valore z:
zj
-1.72 -1.15 -0.81 -0.55 -0.32 -0.11
0.11
0.32
0.55
0.81
1.15
1.73
Il grafico di probabilità corrispondente, zj in funzione di xj (su scale lineari), è mostrato in figura:
2
1,5
1
zj (1)
0,5
0
-0,5
-1
-1,5
-2
8
9
10
11
12
13
14
15
xj (m)
Se i dati di origine fossero distribuiti in maniera perfettamente gaussiana, i corrispondenti punti sul
foglio/grafico di probabilità gaussiana dovrebbero risultare perfettamente allineati lungo una retta.
Si osserva che i punti sperimentali (xj, zj) riportati sul foglio di probabilità gaussiana seguono abbastanza
bene un andamento rettilineo (vedi retta tratteggiata nel grafico), ad eccezione del punto con valore
x12=14.5 m che sembra non appartenere alla distribuzione simil-gaussiana dei rimanenti 11 punti.
Dato che i punti si allineano “discretamente” bene tra loro secondo una retta, i dati di origine (scartato un
punto singolare che risulta “anormale”) seguono con discreta approssimazione una distribuzione gaussiana.
Osservando minuziosamente il grafico, si potrebbe anche concludere che i punti non seguono “perfettamente”
un andamento rettilineo e dunque i dati non sono distribuiti in maniera gaussiana.
Dato che l’andamento dei punti disegnati sul grafico di probabilità non è chiaramente rettilineo (ma neppure
chiaramente non rettilineo), per verificare con maggiore accuratezza la corrispondenza dei dati a una
distribuzione gaussiana potrebbe essere utile disporre di un numero maggiore di dati.
11c)
Disponendo di dati con 3 cifre decimali si ottiene il seguente diagramma rami (metri) e foglie
(decimetri):
Rami
8
9
10
11
12
14
Foglie
9
3 6
1 8 9
1 3 4
2
5
5
Dal diagramma a rami e foglie così ottenuto si evidenzia una discreta, ma non certo ottima, gaussianità dei dati di
origine. Ancora una volta, i dati sono pochi per consentire di trarre conclusioni affidabili sulla loro distribuzione.
_______
Pag. 2/11
Frequenza cumulativa
11d)
10
5
0
8
9
10
11
12
13
14
12
13
14
F. cumulativa relativa
Tempo [m]
[s]
Profondità
1
0.5
0
8
9
10
11
Tempo [m]
[s]
Profondità
31e)
k-esimo percentile: valore superiore al k% delle osservazioni, ed inferiore al (100-k)%.
La formula generale per ricavare l’indice di un generico k-esimo percentile è: Ik = (n+1)k /100
Dall’indice si ricava quindi il valore esatto con un’interpolazione lineare tra i due dati (con indici pari
all’intero prima e dopo di Ik ).
Il 40-esimo percentile ha indice I40% = (12+1)40 /100 = 5.2, quindi il 40-esimo percentile è pari a
40-esimo percentile = 10.8+(10.9-10.8)0.2 = 10.82 m
Per disegnare il box-plot dei dati dobbiamo innanzitutto calcolare la mediana e il primo e il terzo quartile.
I 12 dati ordinati sono X [m]: 8.9 9.3 9.6 10.1 10.8 10.9 11.1 11.3 11.4 11.5 12.2 14.5
La mediana è il 50-esimo percentile, per cui Imediana = (12+1)50 /100 = 6.5, quindi la mediana è pari alla
media del sesto e del settimo dato.
Mediana = (10.9+11.1)/2=11 m =Q2
Il primo quartile è il 25-esimo percentile, con I1Q = (12+1)25 /100 = 3.25, quindi il primo quartile è dato da:
primo quartile = 9.6+(10.1-9.6)0.25 = 9.725 m = Q1
Il terzo quartile è il 75-esimo percentile, per cui I3Q = (12+1)75 /100 = 9.75, quindi il terzo quartile è
compreso tra il nono e il decimo dato, per interpolazione otteniamo:
terzo quartile = 11.4+(11.5-11.4)0.75 = 11.475 m = Q3
La dinamica interquartile vale DIQ= Q3-Q1= 1.75 m
I baffi si possono estendere fino a 1.5DIQ = 2.625 m, quindi fino a 9.725-2.625=7.1 m e
11.475+2.62514.1 m. Ricordiamo comunque che i baffi si fermano all’ultimo dato contenuto entro il limite:
in questo caso sino al dato 1 (baffo inferiore) pari a 8.9 m, e sino al dato 11 (baffo superiore) pari a 12.2 m.
Minimo dato = 8.9 m
Massimo dato = 14.5 m
1
8
9
10
11
12
13
14
15
16
Profondità
[m]
Tempo [s]
_______
Pag. 3/11
Esercizio 2 (25 minuti)
(svolgere su questo foglio e sul retro)
2a)
Un server riceve mediamente 3000 accessi al mese (mese di 30 giorni). Giustificando il tipo di
distribuzione utilizzata, si calcoli la probabilità che in un’ora si abbiano meno di 3 accessi.
2b)
Statisticamente l’80 % degli accessi al server provengono da un dominio straniero (rispetto alla nazione
in cui il server si trova). Su 10 accessi al server quanto è la probabilità che meno di 3 vengano dal
dominio nazionale del server (=non straniero)?
2c)
Considerando un insieme di 1000 accessi al server, quanto vale la probabilità che tra questi almeno 200
(dunque 200 o più) siano nazionali?
32a)
Utilizziamo una distribuzione di probabilità poissoniana, perché la variabile casuale che individua il
tempo di arrivo di un accesso al server è una variabile continua e dunque suddivisibile in sottointervalli di
durata talmente piccola che la probabilità di ricevere più di un accesso nel sottointervallo è zero. Supponendo
che gli arrivi degli accessi al server non siano correlati tra loro e che la probabilità di ottenere un accesso in
un dato intervallo dipenda dalla estensione temporale dell’intervallo, la probabilità di ottenere x accessi
nell’intervallo di tempo cercato è calcolabile dalla PMF di Poisson, con parametro :
PMF di una variabile poissoniana X vale f ( x) 
e   x
,
x!
x  0,1,2...
il suo valor medio vale  =  e la sua varianza vale 2 = .
In questo caso, considerato che ci sono 30 giorni in un mese, il valor medio degli accessi al server
nell’intervallo di tempo è  = 3000 accessi/mese / 30 giorni/mese / 24 ore/giorno = 100/24 accessi = 4.17.
La probabilità che occorrano meno di 3 accessi in 1 ora è uguale a:
e   0 e   1 e   2


 e   e    (1 / 2)e  2  e  (1    0.52 )
P(x<3)= P( x  0)  P( x  1)  P( x  1) 
0!
1!
2!
=e-4.17(1+4.17+0.54.172)=0.0155(5.17+8.68)21.5 %
32b)
Dato che ogni prova è un processo di Bernoulli, le prove sono indipendenti e la probabilità di successo
in ogni prova è costante, la probabilità di x accessi nazionali (non stranieri) su n segue la distribuzione
binomiale, con probabilità di successo p=1-80 %=20 %=0.2. Per cercare la probabilità che meno di 3
accessi siano nazionali, possiamo calcolarla come la probabilità che ce ne siano 0 o 1 o 2:
n
10 
0
P( x  0 successi su 10 prove )  P( x  0)    p x (1  p) nx   0.2 (0.8)10  10.74 %
 x
0
n
10 
1
P( x  1 successi su 10 prove )  P( x  1)    p x (1  p) nx   0.2 (0.8) 9  26.84 %
 x
1
n
10 
2
P( x  2 successi su 10 prove )  P( x  2)    p x (1  p) nx   0.2 (0.8)8  30.20 %
x
2
 
 
n
n!
avendo ricordato che   
 x  x!(n  x)!
Viene richiesta la probabilità che occorrano meno di 3 accessi, che vale quindi:
P(x<3)=P(x=0)+P(x=1)+P(x=2)=01074+0.2684+0.3020=0.6778=67.78 %
_______
Pag. 4/11
42c)
Vista la complessità del calcolo tramite la formula della binomiale (occorrerebbe sommare circa 200
probabilità puntuali, per x da 0 fino a 200, calcolate con la PMF della distribuzione binomiale, e poi
calcolarne il complementare a 1), decidiamo di sfruttare l’approssimazione gaussiana alla binomiale. Il
valor medio vale  = np = 10000.2 = 200. La varianza vale invece 2=np(1-p)=160 e quindi  =12.65.
L’approssimazione è valida in quanto np e n(1-p) sono entrambi molto maggiori di 1 (tipicamente si
considera attendibile l’approssimazione per valori superiori a 5). Nel caso considerato sicuramente
l’approssimazione è buona e dunque per il calcolo utilizziamo una gaussiana con =200 e  =12.65.
Calcoliamo quindi la probabilità tramite standardizzazione:

200  np 
0 

P( x  200)  1  P( x  200)  1  P z 
 1  P z 
  1   ( z  0)  1  50%  50 %


12.65 
np(1  p ) 


e dunque P(“accessi nazionali”≥200)=50 %, come del resto si poteva dedurre immediatamente essendo il
valore discriminante richiesto (200 accessi) pari proprio alla media della variabile distribuita in modo
normale. Per la precisione, dato che x è discreta mentre z è continua, sarebbe più opportuno calcolare:

199.5  np 
 0.5 

 1  P z 
P(x≥200)=1-P(x<199.5)= 1  P z 
  1  P( z  0.0395) =


12
.
65
np
(
1

p
)




=1-(-0.0395)1-(-0.04)=1-0.4840551.6 %
A voler essere ancora più precisi, z=-0.0125 è a lungo la strada tra -0.04 e -0.03 ma occorre interpolare:
P(x≥200)=1-P(x<199.5)=1-(-0.0395)1-[(-0.04)+0.05((-0.03)-(-0.04))=1-[0.48405+0.950.0398]=10.484351.57 %
Il calcolo esatto tramite la distribuzione binomiale (effettuato a calcolatore) fornisce una probabilità pari a
51.3%, che è molto vicina al valore ottenuto con l’approssimazione gaussiana.
Se interessasse sapere la probabilità di avere almeno 200 accessi internazionali:
la media è  = np = 10000.8 = 800 e la varianza vale ancora 2=np(1-p)=160 con  =12.65.

799.5  np 
599.5 

P(x≥800)=1-P(x<799.5)= 1  P z 
 1  P z 
  1  P( z  47.4) 1=100 %.


12.65 
np(1  p) 


_______
Pag. 5/11
Esercizio 3 (20 minuti)
(svolgere su questo foglio e sul retro)
3) Una ditta produttrice di lampadine a basso consumo vuole dimostrare che la vita media delle sue
lampadine è superiore a 10 000 ore. Si considera un campione di 10 lampadine, di cui si misura il tempo di
vita X espresso in migliaia di ore :
X = 17, 8, 11, 9, 18, 12, 6, 15, 10, 11.
3a) Si dia una definizione di Potenza di un test statistico.
3b) Si effettui un test statistico per verificare se la ditta può affermare che la vita media delle sue lampadine è
superiore a 10 000 ore, con livello di significatività pari all’1%.
3c) Che cosa significa e quanto vale il valore P del test effettuato?
3d) La ditta produttrice è convinta che la vita media delle proprie lampadine sia superiore a 10 000 ore. Che
cosa dovrebbe fare per dimostrarlo?
potenza di un test statistico è la probabilità di rifiutare l’ipotesi nulla quando questa è falsa. È
uguale a “uno meno” la probabilità  di errore di tipo II (prob. di accettare l’ipotesi nulla quando è falsa):
Potenza = 1 -  = 1 - P(errore di tipo II) = 1 - P(accettare H0 quando H0 è falsa)
La potenza è un parametro che ci indica la capacità del test di rivelare le differenze della realtà rispetto
all’ipotesi H0 ovvero è la probabilità di riconoscere correttamente la falsità di H0 (quando H0 è falsa).
23a) La
43b) Si
tratta di effettuare un test di valore medio, con varianza ignota. Calcoliamo il valore medio delle 10
misure effettuate (media campionaria):
 1 n
media= X   X i  11.7 kh
n i 1
Non disponendo di altre informazioni sulla varianza, utilizzeremo la varianza dei dati disponibili nel
campione selezionato. Il numero di gradi di libertà è  = n – 1 = 9. La deviazione standard campionaria è:
s(X)=
1 n
X k  X 2 =3.89 kh

n  1 k 1
Effettuiamo quindi un test t (verifica del valor medio con varianza non nota).
1. Il parametro di interesse è la vita media delle lampadine 
2. H0:  = 10 kh
3. H1:  > 10 kh (il test è a un lato solo, in quanto vogliamo dimostrare che la vita media è maggiore a
quella dichiarata)
4. livello di significatività richiesto  = 0.01 (attenzione, su un solo lato)
5. La statistica di test è la statistica t: t 0 
X  X 

sX
s/ n
6. Rifiutiamo H0 se t0 > t,9 = 2.821. (Questo risultato si ricava dalla tabella dei punti percentuale della
distribuzione t, con  = 9, in corrispondenza di una probabilità nella coda destra P= = 0.01)
7. Calcoliamo quindi t0, t 0 
X   X   11.7  10


 1.38
sX
s / n 3.89 / 10
8. Conclusione: dato che t0 = 1.38< 2.821 non possiamo rifiutare l’ipotesi nulla con livello di
significatività 0.01. (in questo caso la soglia di rifiuto è molto lontana).
La durata delle lampadine, secondo il test, non può dirsi superiore a 10 kh con significatività dell’1 %.
_______
Pag. 6/11
valore p, che corrisponde al livello di significatività di soglia tra l’accettazione ed il rifiuto di H0, si
può ricavare direttamente dalla tabella t:
tP = t0 = 1.38, per cui il valore p = T(t0)  10% (valore stimato dalla tabella, sempre per 9 gradi di libertà).
L’interpretazione di questo valore è che l’ipotesi nulla sarebbe stata dichiarata falsa per qualsiasi livello di
significatività  maggiore del 10 %. In questo caso con  = 1 % non si è potuto rifiutare H0.
23c) Il
che la vita media sia realmente maggiore di 10 000 ore, vista l’elevata deviazione standard
del processo, la ditta dovrebbe effettuare altre misure.
All’incirca potrebbero servire una quarantina di dati, infatti nell’ipotesi che la deviazione standard e il valore
23d) Supponendo
medio rimangano gli la stessi, con 40 misure avremmo:
t0 
X   X   11.7  10


 2.76
sX
s / n 3.89 / 40
Per n che quadrupla t0 raddoppia e a fronte della una nuova soglia di accettazione t,40 = 2.423 è ora t0 > t,40
(abbiamo preso 40 gradi di libertà, perché nella tabella non c’è il valore a 39, ma sicuramente è molto simile).
_______
Pag. 7/11
Esercizio 4 (20 minuti)
(svolgere su questo foglio e sul retro)
4) Intendiamo ricavare indirettamente la massa M di un corpo da misure della sua velocità v ed cinetica E.
I risultati sperimentali sono riportati in tabella (si affronta il problema da un punto di vista puramente
teorico-analitico, trascurano le incertezze di misura):
v [m/s]
E [J]
1.00
0.50
1.41
1.83
2.24
4.19
3.16
7.21
4.47
14.54
4a) Individuando variabili opportune che linearizzano la relazione tra le grandezze misurate, si calcoli,
tramite la regressione lineare, il valore M della massa del corpo e si valuti, quantificandola, la presenza di un
eventuale offset nell’energia cinetica anche per velocità nulla.
NOTA: Si ricorda che il coefficiente angolare ed il termine noto della retta di regressione ai minimi quadrati si calcolano come:
m
 x  y   x  x y   y  m x
b
n
n x   x 
n xi yi   xi  y i
2
i
n x   xi 
2
i
2
i
i
2
i
i
i
i
i
2
i
4b) Si riporti in un diagramma cartesiano il grafico della retta di regressione, unitamente ai punti
sperimentali. Si commenti il risultato ottenuto.
OPZIONALE (per 3 punti addizionali)
4c) A partire dal funzionale che descrive la sommatoria degli scarti quadratici dei punti sperimentali dalla
retta di regressione, si ricavino le equazioni - già indicate sopra nella NOTA – che forniscono il coefficiente
angolare e il termine noto della retta di regressione ai minimi quadrati.
54a) La
relazione che fornisce l’energia cinetica in funzione della massa e della velocità è E=(1/2)Mv2. Ci
conviene scegliere due nuove variabili y=E e x=v2 così da ottenere una relazione lineare del tipo y=mx+b,
teoricamente con m=(1/2)M e b=0.
x [(m/s)2]
y [J]
1
0.50
2
1.83
5
4.19
10
7.21
20
14.54
Svolgiamo i calcoli per la regressione lineare ai minimi quadrati sui punti x-y e otteniamo:
coefficiente angolare = m = 0.718 kg e quindi massa M=2m=1.436 kg
termine noto e offset di energia E0 = b = 0.198 J 0.2 J
_______
Pag. 8/11
54b) Riportiamo
in figura i punti sperimentali e la retta di regressione. Visti i punti sperimentali e
confrontati con la retta di regressione, si può concludere che la dipendenza della energia cinetica dalla
velocità al quadrato è effettivamente lineare. Si individua un modesto offset di energia (energia cinetica
osservabile anche in assenza di velocità: E00 quando v=0), che dai conti risulta pari a circa 0.2 J.
16.00
14.00
Costo [€]
12.00
10.00
8.00
y o energia E (J)
6.00
4.00
2.00
0.00
0
5
10
15
20
25
x o velocità alDati
quadrato
[MB] v ((m/s) )
2
2
OPZIONALE (per “5/10” di punti addizionali sull’esercizio)
54c) Lo
scarto i-esimo tra la retta di regressione di equazione y=mx+b e il punto sperimentale i-esimo di
coordinate (xi, yi), è i = yi – [ mxi + b ]
Il funzionale dato dalla sommatoria degli scarti quadratici è:
n
n
i 1
i 1
 (m, b)    i2    yi  mxi  b 2
Per minimizzare tale funzionale, calcoliamo le sue derivate parziali prime, rispetto a m e rispetto a b, e
imponiamole uguali a zero:

 0   m xi2   b xi   xi yi
m
Φ
 0   m xi   nb   yi
b
Abbiamo ottenuto un sistema di due equazione in due incognite, risolvendo il quale si ricava:
m
n xi yi   xi  y i
n xi2   xi 2
 x  y   x  x y   y  m x
b
n
n x   x 
2
i
i
2
i
i
i
2
i
i
i
 y  mx
i
Per verificare che la soluzione ottenuta corrisponde a un minimo (e non a un massimo), si può derivare
ulteriormente la derivata parziale prima e verificare agevolmente che entrambe le derivate seconde sono
positive.
_______
Pag. 9/11
(25 min)
Esercizio 5
(svolgere su questo foglio e sul retro)
5) La misura della massa m di un laptop viene ricavata in due maniere indipendenti:
1. ponendo il laptop su una bilancia digitale con portata 10 kg e 200 livelli si legge mBD=1.1 kg;
2. ponendo il laptop su una bilancia a due bracci e utilizzando come massa di confronto quella di un
volume di acqua, con densità =103 kg/m3 e incertezza di 10-3, complessivamente pari a V=1.11(1) l.
5a) Si ricavino le due misure di massa: valori mBD e mBB e incertezze u(mBD) e u(mBB). Si esprimano i
risultati anche in notazione concisa.
5b) Si discuta la compatibilità tra i due risultati di misura.
5c) Si ricavi la miglior stima della massa m del laptop, ottenuta come media pesata tra le misure compatibili
e la sua incertezza tipo u(m).
5d) Se il numero di gradi di libertà dell’incertezza u(m) viene stimato pari a 30, si ricavi l’incertezza su tale
incertezza, sia in termini assoluti che relativi.
_______
Pag. 10/11
45a) Nella
prima misurazione, con valore mBD=1.1 kg, la risoluzione di misura è finita, con un passo di
quantizzazione mBD=(10 kg)/200=50 g, e pertanto la corrispondente incertezza di quantizzazione è
u(mBD)=mBD/ 12 15 g.
La prima misura è dunque mBD=1100 g15 g o anche mBD=1.100(15) kg.
Nella seconda misurazione, dalla relazione mBB= V si ricava il valore mBB=1.11 kg con una incertezza
relativa ur(mBB)= u r2    u r2 V  . Per il volume ur(V)=0.01/1.11=910-3 e dunque ur2    ur2 V  per cui
ur(mBB)ur(V)=910-3 ed infine u(mBB)=ur(mBB)mBB=10 g.
La seconda misura è dunque mBB=1110 g10 g o anche mBB=1.110(10) kg.
25b) Siamo
in presenza di due misure indipendenti della stessa grandezza che hanno fornito valori diversi tra loro.
Valutiamo la compatibilità tra i risultati delle misure secondo il criterio di compatibilità standard, che prevede di
confrontare la distanza tra i due valori con una combinazione delle due incertezze standard, attraverso la relazione:
mi  m j  kcomp u 2 (mi )  u 2 (m j )
Sostituendo i valori del caso, si ottiene (10 g)<kcomp(22 g) e dunque kcomp ≥ 0.45 e pertanto le due misure sono
compatibili con kcomp = 1.
25c) La
miglior stima della massa del laptop si ottiene come media pesata tra le due misure compatibili, utilizzando
come pesi i reciproci delle corrispondenti incertezze al quadrato:
m1
m
 2 2
u m1  u m2 
m=mMP=
=1108 g
1
1

u 2 m1  u 2 m2 
2
L’incertezza della media pesata è poi:
u(m)=u(mMP)=
1
1
1
 2
u m1  u m2 
u 2 m1   u 2 m2 

=9 g
u 2 m1   u 2 m2 
2
Come prevedibile, la media pesata mMP è compresa tra i valori di m1 e m2 e l’incertezza della media pesata u(mMP)
risulta inferiore sia a u(m1) che a u(m2): abbiamo aumentato il nostro livello di conoscenza sulla massa del laptop.
Il risultato, miglior stima della massa del laptop, è dunque mMP=1108 g9 g o anche mMP=1108(9) g.
25d) Per
l’incertezza relativa dell’incertezza, sappiamo che essa dipende dai gradi di libertà secondo la formula:
ur[u(m)]=1/ 2 pertanto ur[u(m)]=1/ 60 13 % e in termini assoluti u[u(m)]=ur[u(m)]u(m)=1.2 g.
_______
Pag. 11/11