APPUNTI DEL CORSO DI “SISTEMI IMPIANTISTICI E SICUREZZA”
INTRODUZIONE AGLI IMPIANTI ELETTRICI: FONDAMENTI DI ELETTROTECNICA
Sistemi trifase
Già intorno ai 10 kW di potenza installata, gli impianti elettrici sono quasi esclusivamente eserciti in regime di funzionamento
trifase (essendo comunque possibile appropriatamente alimentare anche gli utilizzatori monofase, oltre a quelli trifase).
Le tensioni di alimentazione di un impianto trifase hanno caratteristiche tali da costituire una cosiddetta “terna simmetrica, di
sequenza diretta”.
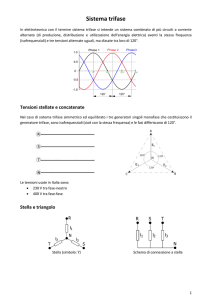
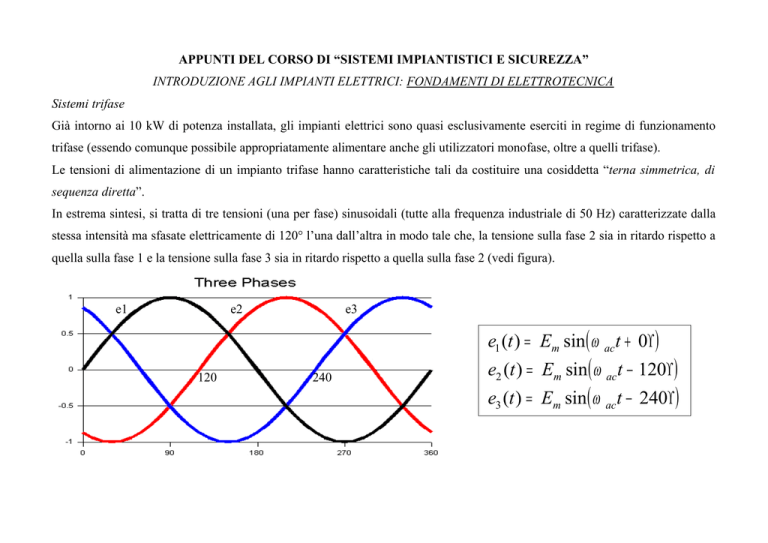
In estrema sintesi, si tratta di tre tensioni (una per fase) sinusoidali (tutte alla frequenza industriale di 50 Hz) caratterizzate dalla
stessa intensità ma sfasate elettricamente di 120° l’una dall’altra in modo tale che, la tensione sulla fase 2 sia in ritardo rispetto a
quella sulla fase 1 e la tensione sulla fase 3 sia in ritardo rispetto a quella sulla fase 2 (vedi figura).
e1
e2
e3
e1 (t ) = Em sin ( ω ac t + 0° )
120
240
e2 (t ) = Em sin ( ω ac t − 120° )
e3 (t ) = Em sin ( ω ac t − 240° )
Sistemi trifase
Nel piano dei “fasori”, le stesse tre tensioni possono essere rappresentate come in figura:
ϕ+
In un sistema trifase è possibile fare uso sia delle tensioni fra
le fasi ed il cosiddetto “centro stella”,
Centro
stella
E1
ed esse prendono il nome di “tensioni stellate”,
V12 = E1 – E2
E3
120°
120°
E2
120°
che delle tensioni fra due diverse fasi,
ed esse prendono il nome di “tensioni concatenate”.
Si mostra facilmente che le tensioni concatenate sono
rappresentabili tramite fasori sfasati di 30° rispetto alle
stellate ed aventi valore efficace √3 volte più grande:
V12 = √3 E1
Anche le tre tensioni concatenate (V12, V23, V31) costituiscono una terna simmetrica di sequenza diretta.
Sistemi trifase
Se si alimenta un impianto elettrico trifase simmetrico (per esempio, conduttori elettrici delle tre diverse fasi identici) con una
terna di tensioni simmetriche come quella appena vista, anche le terne delle correnti circolanti sui rami di un tale impianto
saranno simmetriche, e per esse valgono considerazioni perfettamente simili a quelle svolte per le tensioni.
Ciò posto, è possibile evidenziare una prima proprietà molto importante delle terne simmetriche (di tensioni e/o di correnti):
la somma delle tre grandezze è sempre pari a zero (ovviamene, sia nel dominio del tempo che nel dominio dei fasori).
Nel centro stella le correnti si annullano;
quindi, anche quando è presente un collegamento elettrico (conduttore) tra il centro stella ed il terreno o tra il centro stella di un
carico trifase e quello del sistema di alimentazione (se c’è, quest’ultimo conduttore prende il nome di “neutro”), in questo
collegamento non circola corrente.
Ne consegue, per esempio, che sul conduttore di neutro non si hanno ne perdite (per effetto Joule) ne “cadute di tensione”.
Sistemi trifase
Un semplice circuito trifase può essere rappresentato graficamente come nella seguente figura.
Centro stella
Importante !!
Carico trifase a stella
e1(t)
e2(t)
v12(t) !!
e3(t)
iN = 0 !!
iN = 0 !!
Carico trifase
a triangolo
Neutro, N
P4
Carico monofase
P1 =
P2 = P2 P3
Carico trifase + N
Sistemi trifase
Nei sistemi trifase, la potenza complessiva è pari alla somma delle potenze sulle singole fasi.
Se il sistema trifase è caricato in modo equilibrato (carichi uguali su tutte e tre le fasi) allora le potenze sulle singole fasi sono
uguali tra loro, e la potenza complessiva è pari a quella su una singola fase moltiplicata per tre.
In altri termini:
S1 = E1 I1 , S 2 = E2 I 2 ,
S3 = E3 I 3 ,
St = S1 + S 2 + S3
P1 = E1 I1 cos ϕ 1 , S 2 = E2 I 2 cos ϕ 2 ,
S3 = E3 I 3 cos ϕ 3 ,
Pt = P1 + P2 + P3
Q1 = E1 I1 sin ϕ 1 , S 2 = E2 I 2 sin ϕ 2 ,
S3 = E3 I 3 sin ϕ 3 ,
Qt = Q1 + Q2 + Q3
In condizioni di equilibrio:
St = 3 E I =
3V I
Pt = E I cos ϕ =
3 V I cos ϕ
Qt = E I sin ϕ =
3 V I sin ϕ