Isp_05.5.13

Istituzioni di Statistica e Probabilità - Scienze Geologiche – a.a. 04/05
Istituzioni di Statistica e Probabilità
Scienze Geologiche – a.a. 04/05
Prova scritta – 13 maggio 2005
Cognome
Nome
Parte teorica
All’occorrenza, evidenziare la risposta che si ritiene corretta.
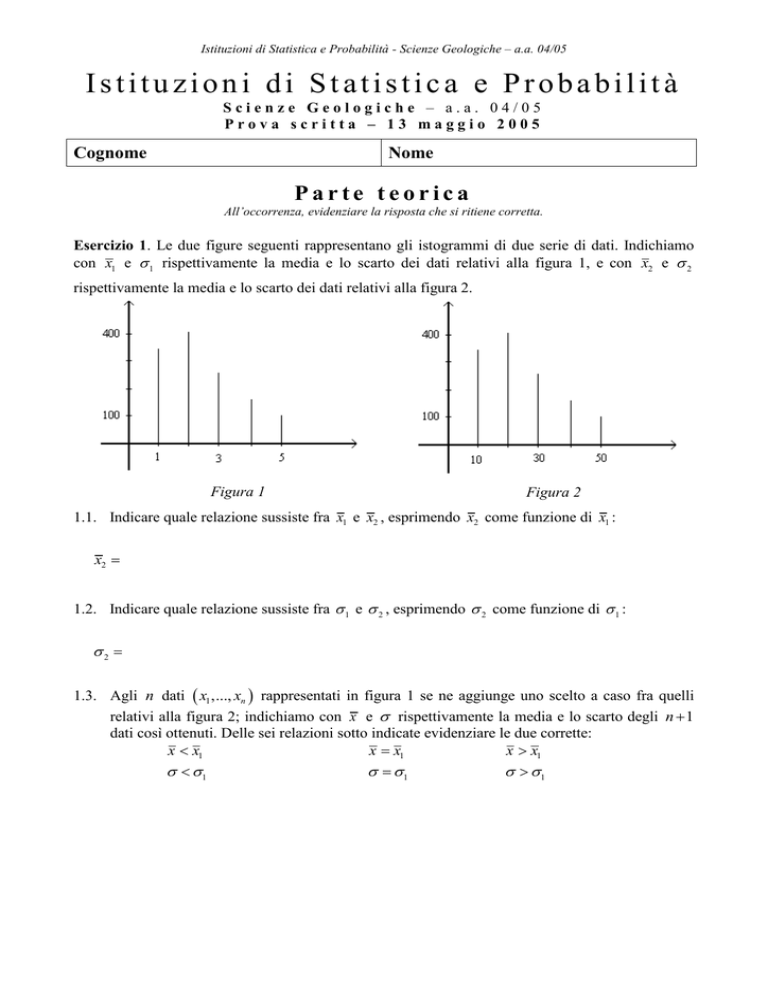
Esercizio 1. Le due figure seguenti rappresentano gli istogrammi di due serie di dati. Indichiamo
con x1 e  1 rispettivamente la media e lo scarto dei dati relativi alla figura 1, e con x2 e  2
rispettivamente la media e lo scarto dei dati relativi alla figura 2.
Figura 1
Figura 2
1.1. Indicare quale relazione sussiste fra x1 e x2 , esprimendo x2 come funzione di x1 :
x2 
1.2. Indicare quale relazione sussiste fra  1 e  2 , esprimendo  2 come funzione di  1 :
2 
1.3. Agli n dati  x1 ,..., xn  rappresentati in figura 1 se ne aggiunge uno scelto a caso fra quelli
relativi alla figura 2; indichiamo con x e  rispettivamente la media e lo scarto degli n  1
dati così ottenuti. Delle sei relazioni sotto indicate evidenziare le due corrette:
x  x1
x  x1
x  x1
  1
  1
  1
Istituzioni di Statistica e Probabilità - Scienze Geologiche – a.a. 04/05
Esercizio 2. Nella figura sotto sono rappresentati valori di coppie di dati quantitativi (ogni punto
rappresenta una coppia di dati); sogno segnati gli assi che passano per il punto medio dei dati.
Delle tre rette sotto indicate una è quella di regressione; individuare quale, spiegandone il perché
(eventualmente esplicitando le ragioni di esclusione delle altre due)
r1
1
y   x  20
3
r2
1
y   x2
3
r3
1
y x
3
Esercizio 3. Una variabile quantitativa, definita sugli elementi di una popolazione, ha media
sconosciuta e varianza nota. Due campioni vengono utilizzati per testare l’ipotesi che la media della
popolazione abbia valore 50. I due campioni hanno numerosità n1  150 il primo e n2  250 il
secondo; le rispettive medie campionarie sono uguali: x1  x2 . Indichiamo con p1 e con p2 i
rispettivi p-valori. Si può dire quale delle seguenti relazioni è quella corretta (se SI, evidenziarla; se
NO, darne una breve giustificazione)?
p1  p2
p1  p2
p1  p2
Istituzioni di Statistica e Probabilità - Scienze Geologiche – a.a. 04/05
Istituzioni di Statistica e Probabilità
Scienze Geologiche – a.a. 04/05
Prova scritta – 13 maggio 2005
Cognome
Nome
Esercizio 1. A fianco è riportato l’istogramma
del numero di fiori sbocciati su alcuni rami di
una pianta.
1.3. Indicare il numero di fiori conteggiati
m
1.1. Costruire la tabella seguente:
xi
ni
xini
xi2
xi2ni
1
2
3
4
1.4. Riportare, nella tabella sottostante, le
formule che consentono di calcolare le
grandezze indicate a partire dai valori
5
6
Totali
#####
1.2. Indicare il numero di rami esaminati
n
Formula (letterale)
Grandezza
media x
varianza 2
scarto 
determinati nella tabella a sinistra; quindi
calcolare il valore numerico di tali grandezze.
Valore numerico
x
x
 2 
2 


Istituzioni di Statistica e Probabilità – Scienze Geologiche – a.a. 04/05
Esercizio 2. Una variabile quantitativa, definita sugli elementi di una popolazione, ha media 
sconosciuta e scarto quadratico medio   1.44 . Un campione di 144 elementi ha media uguale a
49.95. Si vuole testare, al livello   1% , l’ipotesi che la popolazione abbia media   50 .
2.1. Calcolare il p-valore (precisando la formula utilizzata)
p-valore =
2.2. Confrontare il p-valore col livello e dedurre da tale confronto quale è la conclusione.
Esercizio 3. La variabile qualitativa X può assumere le due modalità A e B; la variabile qualitativa Y
può assumere le due modalità C e D. Un campione di osservazioni della coppia (X, Y) fornisce i
risultati riportati nella tabella:
A
B
Totale
C
452
748
1200
D
548
1252
1800
Totale
1000
2000
3000
3.1. Calcolare le frequenze teoriche relative al test  2 di indipendenza, e riportarle nella seguente
tabella.
A
B
Totale
C
1200
D
1800
Totale
1000
2000
3000
3.2. Dire se, in base al test 2 al livello del 5% , le variabili X e Y risultano dipendenti o
indipendenti.