Raddrizzatori controllati

Raddrizzatori controllati
• I Diodi sono sostituiti da SCR
• viene controllato (ritardandolo) l’istante di innesco
• lo spegnimento avviene come per i Diodi (“naturale”)
Æ il valor medio della tensione lato dc può essere
solo abbassato (rispetto al caso di raddrizzatore
non controllato a Diodi)
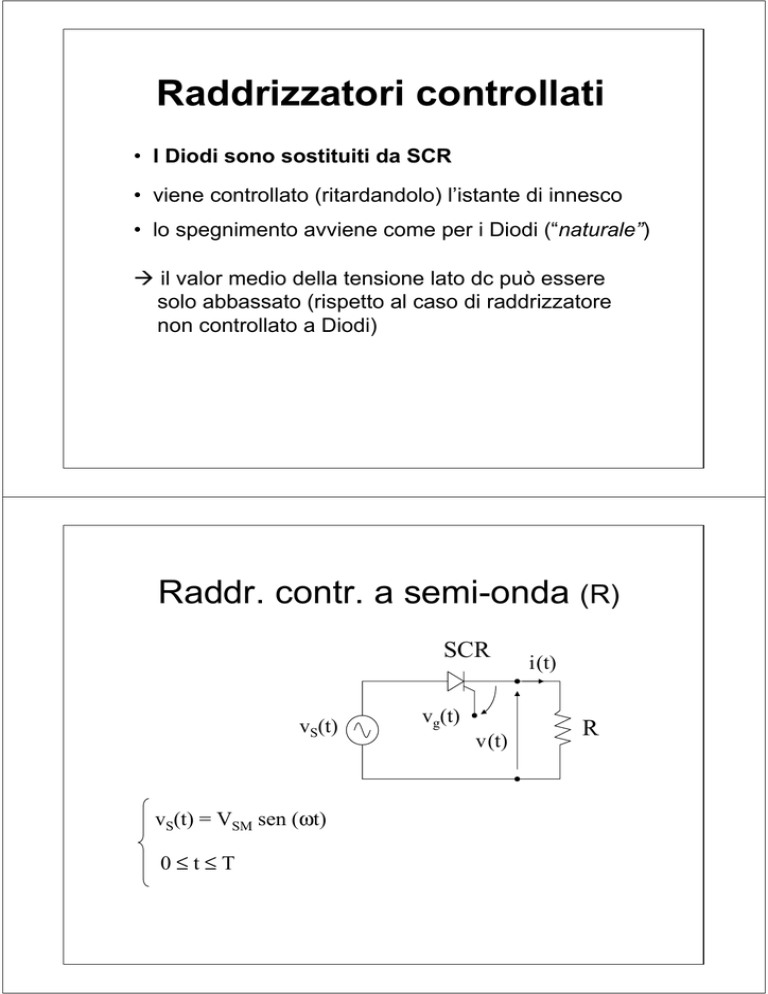
Raddr. contr. a semi-onda (R)
SCR
vS(t)
vS(t) = VSM sen (ωt)
0≤t≤T
vg(t)
v(t)
i(t)
R
Raddr. contr. a semi-onda (R)
v(t)
vS(t)
i(t)
π
0 α∗
2π
ωt
vS(t)
vg(t)
0 t∗
t
T T+ t∗
T/2
Raddr. contr. a semi-onda (R)
v(t) ≅
VSM sen (ωt)
0
i(t) ≅
VSM/R sen (ωt)
t* ≤ t ≤ T/2
T/2 ≤ t ≤ T+ t*
0
Vdc
1 2π
v(α )dα
= v(T ) = Vo =
2π 0
Vdc
VSM π
V
π
=
senα dα = SM [− cos α] α*
2 π α*
2π
∫
Vdc =
∫
VSM 1 + cos α * VSM
α*
=
cos 2
π
π
2
2
α* < π
non controllato
Raddr. contr. a semi-onda (R-L)
SCR
vg(t)
vS(t) = VSM sen (ωt)
i(t)
R
v(t)
periodo T
L
Raddr. contr. a semi-onda (R-L)
vS(t)
stessa area
( R=1 Ω )
v(t)
vR(t)
i(t)
0 α∗
π
π+β
vS(t)
2π
ωt
Raddr. contr. a semi-onda (R-L)
Vdc
VSM π +β
V  cos β + cos α * 
senα dα = SM 
=

π 
2 π α*
2

∫
non controllato
Vdc =
VSM
α *+ β
α *− β
cos
cos
2
2
π
Raddr. contr. a semi-onda (altri)
Considerazioni analoghe al caso di raddrizzatore
non controllato per:
• diodo di libera circolazione
• carico R-E (R-L-E)
• carico R-C
Vedi esercitazioni PSpice
Raddr. contr. ad onda intera (R)
S1
vS(t)
i(t)
S2
v(t)
S3
R
S4
Raddr. contr. ad onda intera (R)
Rappresentazione a rami
i(t)
vS(t)
S1
S3
v(t)
S2
S4
R
Raddr. contr. ad onda intera (R)
v(t)
vS(t)
i(t)
π
0 α∗
2π
ωt
vg(t)
0 t∗
T/2 T/2+ t∗
S2-S3
S1-S4
t
T T+ t∗
S1-S4
Se il controllo non è simmetrico
Æ f1 = 50 Hz invece di 100 Hz
Raddr. contr. ad onda intera (R)
Vdc
1 π
v(α )dα
= v (T ) = Vo =
π 0
Vdc
VSM π
V
=
senα dα = SM [− cos α ] απ *
π α*
π
∫
Vdc =
∫
2
1 + cos α * 2
α*
VSM
= VSM cos 2
2
2
π
π
non controllato
Raddr. contr. ad onda intera (R-L)
v(t)
vS(t)
i(t)
∗
0 α
π π+α∗
2π
ωt
iS(t)
modo “continuo”
Æ controllo completo Vdc
Raddr. contr. ad onda intera (R-L)
Vdc
VSM π + α *
V
=
senα dα = SM [− cos α ] απ +* α *
π α*
π
Vdc =
∫
1
2
VSM [cos α* − cos( π + α*)] = VSM cos α*
π
π
0 ≤ α* ≤ π
non controllato
tensione lato dc (+
+) o (−
−)
solo in transitorio se il carico non è attivo
Raddr. contr. ad onda intera (Io)
v(t)
vS(t)
Io
i(t)
∗
0 α
π π+α∗
2π
ωt
π π+α∗
2π
ωt
iS(t)
0 α∗
considerazioni sul
legame tra Pdc e Pac
Raddr. contr. ad onda intera (Io)
Calcolo delle potenze medie Pdc e Pac
Pdc =
1
T
∫
v(t )i (t )dt = I o
T
Pac = V I1 cos ϕ1 =
1
T
∫
T
v(t )dt = Vdc I o =
2
VSM I o cos α*
π
VSM 4 I o
2
cos α* = VSM I o cos α*
π
2 π 2
(trascurando le cadute di tensione sugli SCR)
Raddr. contr. ad onda intera (R-L)
Considerazioni analoghe al caso di raddrizzatore
non controllato per:
• diodo di libera circolazione
• carico R-E (R-L-E)
• carico R-C Æ attenzione ai dv/dt !
Vedi esercitazioni PSpice
Raddrizzatori controllati trifase
Derivano direttamente dai corrispondenti non controllati
sostituendo tutti i Diodi con SCR
• trifase a semi-onda (mezzo ponte)
• trifase ad onda intera (ponte completo)
Anche in questo caso si possono considerare soluzioni
“ibride” con Diodi ed SCR.
Raddrizzatori controllati trifase
semi-onda
i(t) = Idc
Lato “alto”
v + (t)
S1
S2
S3
v(t)
Idc
neutro
0
eS1(t) eS2(t) eS3(t)
Raddrizzatori controllati trifase
semi-onda
2/3 π
v + (t)
v(t)
0
π
2π
ωt
π/6+α∗ 5/6π+α∗
eS2 (t)
eS3 (t)
eS1 (t)
Vdc= 3√3/2π ESM cos α∗
Raddrizzatori controllati trifase
onda intera
i(t) = Idc
S1
S2
S3
eS1(t)
v(t)
Idc
eS2(t)
eS3(t)
S4
S5
S6
Vdc= 3√3/π ESM cos α∗ = 3/π VSM cos α∗
Raddrizzatori
controllati trifase
onda intera