Introduzione al corso di Programmazione

Introduzione al corso di Programmazione
Sabrina Mantaci
A.A.2004-2005
1
Il Computer
Supponiamo di volere risolvere un’equazione di secondo grado:
ax2 + bx + c = 0
Per trovare la soluzione dobbamo svolgere diversi passi:
1. Determinare il ∆ = b2 − 4ac;
2. Studiare il segno del ∆:
(a) Se
√ ∆ > 0, allora determinare le soluzioni x1 = (−b +
∆)/2a;
√
∆)/2a e x2 = (−b −
(b) Se ∆ < 0 non ci sono soluzioni reali;
(c) Se ∆ = 0 le due soluzioni coincidono e sono x1 = x2 = −b/2a.
Se è dato questo metodo per la risoluzione delle equazioni, sono dati i parametri del
problema (nel nostro caso i coefficienti a, b, c), se abbiamo la possibilità di memorizzare
i dati parziali su un supporto fisico (come, per esempio della carta da minuta), e se
abbiamo una calcolatrice per effettuare i calcoli, siamo in grado di determinare facilmente
le soluzioni.
In pratica, una volta che qualcuno fornisce il metodo di risoluzione e i dati del problema, il lavoro dell’esecutore è talmente semplice da poter essere svolto da un dispositivo
automatico in grado di leggere i dati e di eseguire le istruzioni del procedimento descritto.
Indipendentemente dalle modalità con cui realizziamo questi dispositivi nella pratica, dal punto di vista concettuale, un calcolatore deve essere costituito dai seguenti
componenti di base:
1. Memoria: permette di memorizzare la procedura, i dati iniziali, i risultati intermedi, i risultati finali;
1
2. Funzione aritmetica: permette di effettuare operazioni aritmetiche sui dati;
3. Ingresso/uscita: dispositivi atti a ricevere dati dall’esterno e a comunicare i
risultati all’esterno;
4. Controllo: serve ad eseguire i passi della procedura, coordinando il flusso dei dati
tra i vari componenti.
Più in dettaglio, i calcolatori elettronici sono formati dalle seguenti componenti:
• La memoria del calcolatore è costituita da due parti principali. Una parte è detta
unità RAM (Random Access Memory - Memoria ad accesso casuale) ed è
costituita da una successione ordinata di celle o registri, ciascuno dei quali è capace
di memorizzare una stringa di bit (binary digit - cifra binaria, ossia 0 o 1) di lunghezza
fissata dipendente dal tipo di calcolatore (in genere 8 o multipli di 8) detta parolamacchina. Le celle sono numerate da 0 a k − 1: si dirà allora che la memoria ha
dimensione k. Ciascuno dei numeri da 0 a k − 1 denota una locazione o indirizzo di
memoria. In particolare la locazione di memoria 0 prende il nome di accumulatore
ed è la cella dove viene conservato il risultato dell’ultima operazione effettuata dal
calcolatore.
Un’altra parte della memoria, detta unità ROM (Read Only Memory - Memoria
a sola lettura), contiene dati e programmi inalterabili, come, ad esempio, i codici di
caratteri e il sistema operativo.
• Il processore o CPU (Central Processing Unit) è il vero e proprio “cervello”
del computer. L’attività principale della CPU consiste nel recuperare le istruzioni
da eseguire, decodificarle ed eseguirle. La CPU è costituita da due parti principali,
l’ALU e la CU. L’ ALU (Arithmetic Logic Unit) è la parte attiva del sistema dove vengono eseguite operazioni aritmetiche (+,-,*,/) e le elaborazioni logiche
(confronti e operazioni logiche). I dati vengono letti dalla memoria e scritti nella
memoria facendo in modo che il processore contenga solo i dati di volta in volta
necessari. La CU (Control Unit) si occupa di dirigere il flusso dei dati all’interno del processore, andando a cercare nella memoria i dati che gli sono necessari e
depositando nella memoria i dati elaborati.
• Unità di INPUT è un qualunque dispositivo che permette di immettere i dati
dall’esterno (ad esempio la tastiera o il mouse).
• Unità di OUTPUT è invece un qualunque dispositivo che permette di visualizzare
all’esterno i risultati del calcolo (ad esempio la stampante o lo schermo).
2
2
La risoluzione dei problemi
In questo corso siamo interessati ad imparare delle tecniche che ci permettano di scrivere
dei programmi informatici per la soluzione di determinati problemi, che possono essere
formalizzati in termini matematici. Per questo vogliamo stabilire quali sono i passi fondamentali che ci permettono di arrivare ad una soluzione di un dato problema. La soluzione
di un problema nel nostro ambito consiste infatti di diversi passaggi, ognuno dei quali
deve essere preso in considerazione nella progettazione di un programma:
• definizione del problema: si deve definire e formalizzare il problema che ci poniamo;
• caratterizzazione della soluzione: bisogna specificare qual’è l’output che vogliamo
che il nostro programma ci fornisca;
• sviluppo di un algoritmo: questa è la fase più importante del progetto, ossia quella
di stabilire quale metodo che intendiamo utilizzare per fornire una soluzione al
problema;
• codifica dell’algoritmo. Questa è fase di programmazione propriamente detta, ossia
la traduzione dell’algoritmo in un particolare linguaggio di programmazione;
• verifica del programma: una volta che il programma è stato scritto, si deve verificare
che da una risposta corretta al problema;
• documentazione della soluzione: consiste nell’integrare il programma con dei commenti che assolvono al compito di rendere il programma leggibile, e, di conseguenza, più facile da correggere, da modificare, adattare e da condividere con altri
programmatori;
• manutenzione: consiste nel tenere il programma aggiornato con modifiche che rispondono alle nuove esigenze delle specifiche del problema.
3
Gli Algoritmi
Ci concentriamo qui sulla fase più importante della progettazione di un programma. Supporremo che sia già stato formalizzato il problema e stabilito quali sono le risposte che
vogliamo dal programma.
La definizione di Informatica data dall’ACM (Association for Computing Machinery) è la seguente: l’informatica è lo studio sistematico degli algoritmi che descrivono e
trasformano l’informazione: la loro teoria, analisi, progetto, efficienza, realizzazione ed
applicazione.
In questa definizione viene utilizzata la nozione di “algoritmo” che può informalmente
essere definito come un “metodo” per la risoluzione di un problema specifico.
3
Per avere un’intuizione su cosa sia un algoritmo, possiamo pensare per esempio a
una ricetta di cucina: vengono definiti tutti gli ingredienti e le dosi, e infine vengono
date le istruzioni per l’esecuzione, in cui si descrivono ordinatamente tutti i passi che si
devono svolgere per ottenere il risultato finale. Oppure pensiamo alle istruzioni per l’uso
del videoregistratore, che descrivono passo dopo passo tutto quello che si deve fare per
farlo funzionare (collegare il videoregistratore al televisore; inserire la spina; accendere il
videoregistratore; inserire la cassetta; premere il tasto “play”).
Diamo qui una definizione più formale:
Definizione 3.1 Un algoritmo è un insieme finito di regole che dà una sequenza delle
operazioni da svolgere al fine di risolvere un problema specifico.
Un algoritmo deve soddisfare le seguenti proprietà fondamentali:
1. Finitezza: un algoritmo deve sempre terminare dopo un numero finito di passi.
Ogni volta che si scrive un algoritmo bisogna sempre verificare che a un certo punto
termini.
2. Non ambiguità: in un algoritmo ogni passo deve essere ben specificato, in modo
che un esecutore (umano o automatico) sappia esattamente e in maniera univoca (o
deterministica) cosa deve fare ad ogni passo. L’uso dei linguaggi di programmazione
permette di eliminare certe ambiguità che sono presenti nei linguaggi naturali.
3. Input: un algoritmo ha zero o più input, che sono i dati che vengono forniti prima
che il calcolo abbia inizio, e sui quali vengono svolte le computazioni;
4. Output: un algoritmo ha uno o più output, che rappresentano i risultati del
problema, quantità che hanno una specifica relazione con gli inputs;
5. Realizzabile praticamente: tutte le operazioni che sono descritte nell’algoritmo
devono essere sufficientemente semplici da poter essere, in linea di principio, eseguite
in tempo finito da un uomo con carta e penna.
Inoltre ad un algoritmo si richiede che sia corretto ed efficiente. Un algoritmo è
corretto se perviene alla soluzione del compito a cui è preposto. Un algoritmo è efficiente
se perviene alla soluzione del problema nel modo più veloce possibile e usando la più
piccola quantità possibile di risorse fisiche (memoria).
Diamo ora alcuni esempi di algoritmi, partendo da alcuni problemi più semplici, fino
ad arrivare alla formalizzazione algoritmica un problema matematico classico.
Esempio: Supponiamo di avere un pallottoliere con tre file di palline. Vogliamo effettuare la somma di due numeri utilizzando il pallottoliere. Supponiamo che la prima riga
rappresenti il primo addendo e la seconda riga il secondo addendo, mentre la terza riga
conterrà il risultato della somma. Nella prima e nella seconda riga disponiamo sul lato
4
sinistro tante palline quanto è il valore del primo e del secondo addendo, rispettivamente.
Nella terza riga tutte le palline si trovano sul lato destro. Ci muoviamo come segue:
1. nella prima riga, si sposta una pallina da sinistra a destra e, contestualmente, nella
terza riga se ne sposta una da destra a sinistra.
2. si ripete l’operazione precedente finché non si è svuotata la prima riga.
3. non appena la prima riga è vuota, nella seconda riga si sposta una pallina dalla
sinistra alla destra e, contestualmente, nella terza riga se ne sposta una da destra a
sinistra.
4. si ripete l’operazione precedente finché non si è svuotata la seconda riga.
5. il numero di palline che si trova nel lato sinistro della terza riga al termine delle
operazioni è il risultato cercato.
Esempio: Supponiamo di volere cercare il titolo di un libro in uno schedario di una
biblioteca. Se non abbiamo alcuna informazione su come è organizzato lo schedario,
l’algoritmo che possiamo utilizzare è il seguente:
1. si esamina la prima scheda dello schedario;
2. se il titolo coincide con quello cercato allora terminiamo la ricerca. Altrimenti si
passa alla scheda successiva.
3. si continua cosı̀ fino a quando si trova la scheda cercata oppure si arriva all’ultima scheda. Nel primo caso estraiamo la scheda cercata, mentre nel secondo caso
possiamo affermare che la ricerca è fallita, cioè il libro non è presente nella biblioteca.
È facile notare che questo algoritmo può essere molto “costoso” in termini di tempo.
Infatti nel caso peggiore occorrerà consultare tutte le schede, che sono tante quante i libri
presenti nella biblioteca. È per questo che molte volte è utile organizzare i titoli in ordine
lessicografico. In tal caso la ricerca può essere resa molto più rapida, seguendo l’algoritmo
descritto qui di seguito.
1. si prende la scheda centrale dello schedario;
2. se la scheda è quella cercata, la ricerca si interrompe;
3. in caso contrario, se il titolo del libro precede in ordine lessicografico quello della
scheda appena estratta, si ripete il procedimento nella metà dello schedario che
precede la scheda estratta. In caso contrario si procederà alla ricerca nel gruppo di
schede che seguono la scheda estratta.
5
Si intuisce che il secondo algoritmo proposto giunge alla soluzione più velocemente del
precedente, in quanto in nessun caso esamina tutte le schede (ad ogni passo ne esclude la
metà). In particolare, come vedremo da un’analisi più precisa, esaminerà un numero di
schede proporzionale al logaritmo in base 2 del numero di libri nella biblioteca, riducendo
drasticamente il tempo della ricerca. Questa osservazione mette in evidenza come oltre al
problema di determinare un algoritmo per la soluzione di un problema, ci interesseremo a
trovare l’algoritmo più efficiente possibile. Oltre a questo, è importante osservare che un
altra fase fondamentale nella progettazione di un algoritmo è quella di strutturare i dati
in maniera tale da rendere più efficiente l’applicazione dell’algoritmo stesso. Per esempio,
ci siamo resi conto che nella gestione di un archivio, è conveniente mantenere le schede
ordinate, in maniera tale da facilitare la fase di ricerca. Questo viene realizzato mediante
strutture dati adatte alla gestione di operazioni di dizionario (inserimento, cancellazione
e ricerca).
Esempio: Dati due interi a e b, vogliamo calcolare il massimo comun divisore (M CD)
di a e b. Ricordiamo che:
Definizione 3.2 Il massimo comun divisore (MCD) tra due interi a e b è un intero q
tale che q divide a e b, e se p è un altro divisore di a e b, allora p divide q.
Esistono diversi algoritmi per determinare il M CD fra due numeri, ma il più efficiente
è il cosiddetto Algoritmo di Euclide. Tale algoritmo è basato sul seguente teorema:
Teorema 3.1 (algoritmo della divisione) Sia a un intero e d un intero positivo.
Allora esiste un’unica coppia di interi q ed r con 0 ≤ r ≤ d tale che a = dq + r.
Lemma 3.1 Sia a = bq + r dove a, b, q, r sono interi. Allora M CD(a, b) = M CD(b, r).
Dimostrazione: Se d divide a e d divide b allora d divide r = a − bq. Viceversa, se d
divide b e d divide r, allora d divide a = bq + r. 2
Il lemma appena enunciato ci dà la possibilità di trovare un “metodo” per stabilire
qual’è il M CD tra due numeri. Siano a e b due interi positivi con a ≥ b. Sia r0 = a,
r1 = b. Allora possiamo applicare ripetutamente l’algoritmo della divisione e ottenere:
r0 = r1 q1 + r2
r1 = r2 q2 + r3
···
rn−2 = rn−1 qn−1 + rn
rn−1 = rn qn
0 ≤ r2 < r1
0 ≤ r3 < r2
0 ≤ rn < rn−1
Per il lemma si ha:
M CD(a, b) = M CD(r0 , r1 ) = M CD(r1 , r2 ) = · · · = M CD(rn−1 , rn ) = M CD(rn , 0) = rn
6
Dunque il massimo comun divisore è l’ultimo resto non nullo nella sequenza delle
divisioni. L’algoritmo di Euclide si può quindi esprimere nella seguente forma:
Algoritmo di Euclide
1. x ← a, y ← b;
2. dividi x per y e sia r il resto della divisione;
3. se r = 0 l’algoritmo termina, e y sarà il MCD;
4. altrimenti poni x ← y, y ← r e torna al passo 2.
Questo algoritmo termina perchè i valori di x e y sono non negativi decrescenti. Inoltre
questo algoritmo calcola correttamente il M CD per quanto dimostrato dal lemma.
4
Complessità degli Algoritmi
Lo studio della complessità di un algoritmo consiste nel determinare la quantità di risorse
impiegate durante esecuzione dell’algoritmo su un input di taglia generica n. Fra queste
terremo in particolare considerazione due grandezze fondamentali: il tempo di calcolo e lo
spazio di memoria utilizzata. Nel primo caso conteremo il numero di operazioni elementari svolte dall’algoritmo su un input di taglia n. Si parla in questo caso di complessità
di tempo. Nel secondo caso calcoleremo la quantità di locazioni di memoria che devono
essere utilizzate nello svolgimento dell’algoritmo. In questo caso parleremo di complessità di spazio. In questo corso prenderemo principalmente il tempo come parametro
per calcolare l’efficienza di un algoritmo. Quindi, dati due programmi che risolvono lo
stesso problema, diremo che il più efficiente è quello che impiega il minor tempo nella
sua esecuzione. Se considerassimo un’unità di misura standard per il tempo, come i secondi, un possibile metodo di confronto potrebbe consistere nel mandare in esecuzione
i due programmi e vedere quale dei due finisce prima i suoi calcoli. Ma questo metodo
di valutazione non è attendibile se non consideriamo le condizioni in cui si effettuano le
prove. Bisogna infatti tener conto:
• dell’elaboratore su cui il programma viene eseguito. Il confronto fra due programmi
sarà valido solo se li mandiamo in esecuzione sullo stesso elaboratore;
• del particolare compilatore. Infatti compilatori diversi possono generare programmi
in linguaggio macchina con caratteristiche diverse;
• dei dati di ingresso. Per confrontare l’efficienza di due programmi essi devono essere
eseguiti sullo stesso insieme di dati di ingresso.
7
• della significatività dei dati di ingresso, perché per confrontare l’efficienza di due
programmi, essi devono essere eseguiti più volte su dati differenti.
Anche ammesso che il test venga fatto sugli stessi dati, può succedere che uno dei due
programmi si comporti meglio su un certo input e peggio su un altro. Qual’è quindi un
criterio oggettivo di valutazione dell’efficienza di un programma?
Un’analisi oggettiva del tempo di computazione deve ignorare tutti i fattori che dipendono dalla macchina, dal compilatore, dai dati di input utilizzati e i dettagli implementativi legati al linguaggio di programmazione utilizzato.
Cercheremo quindi di associare ad ogni algoritmo una funzione della dimensione dei
dati di input, che ci permetta di definire in maniera oggettiva la complessità di tempo
dell’algoritmo. A tal fine dobbiamo fare delle semplificazioni. Considereremo che:
• il costo di esecuzione di ogni istruzione semplice (assegnazione, lettura, scrittura,
operazioni aritmetiche e logiche) è 1;
• il costo di esecuzione di un’istruzione composta è pari alla somma delle istruzioni
semplici che la compongono;
• il costo di un ciclo è dato dal costo delle istruzioni del ciclo più il costo del test di
fine ciclo, moltiplicato per il numero di volte che il ciclo viene eseguito;
• il costo di un’istruzione condizionale è dato dal costo del test più il costo delle
istruzioni che vengono eseguite se la condizione è vera;
• il costo di attivazione di un sottoprogramma è pari al costo di esecuzione delle
istruzioni che compongono il sottoprogramma.
Si può pensare che assegnare a tutte le istruzioni semplici valore 1 sia una semplificazione troppo forte. Infatti questo equivarrebbe a dire che, per esempio, le istruzioni a:=a+1
e a:=b+(c*b)/(a+c)+2 valgono entrambe 1, malgrado la seconda appaia più complessa
della prima. Ma si può osservare che se t1 è il tempo che occorre a calcolare la prima
istruzione e t2 il tempo necessario a calcolare la seconda, allora possiamo sempre trovare
una costante c tale che t2 < c · t1 . Quindi possiamo dire che le due istruzioni hanno lo
stesso costo, a meno di un fattore costante. Le stesse considerazioni si possono fare per la
valutazione delle altre istruzioni. Possiamo concludere che la nostra valutazione del costo
di un programma è approssimata per un fattore moltiplicativo c e che è indipendente dal
tipo di calcolatore, programma o compilatore usato.
Fatte queste considerazioni, come determiniamo qual’è la funzione che ci dà una valutazione della complessità di un algoritmo? Osserviamo che il tempo di esecuzione di
un programma dipende dai suoi dati di ingresso. Infatti prendiamo ad esempio il problema della ricerca di una scheda in un archivio. In questo caso, indipendentemente dal
8
programma utilizzato, tanto più grande è l’archivio, tanto più tempo impiegherà il programma a trovare la scheda cercata. Una valutazione dell’efficienza di un algoritmo sarà
quindi una funzione della dimensione dell’input. Per dimensione dell’input si intende la
quantità di memoria necessaria per memorizzare i dati di input del problema. Infatti il
numero di istruzioni semplici eseguite da un programma dipende molto da come è fatto
l’input. Quindi, quali input dobbiamo considerare di volta in volta?
Consideriamo ancora una volta il problema della ricerca in un archivio. Supponiamo
che l’archivio non sia ordinato e dobbiamo quindi fare una ricerca esaustiva. Se l’elemento
da cercare è il primo dello schedario, siamo fortunati e dobbiamo fare una sola operazione
di confronto. Ma se l’elemento cercato è l’ultimo dello schedario, o addirittura non è
contenuto nell’archivio, faremo un numero di confronti uguale al numero delle schede
presenti. È chiaro che, per avere una valutazione oggettiva sul costo di esecuzione di un
algoritmo, la valutazione non deve dipendere dal particolare dato di ingresso. Proprio per
questo il costo del programma verrà valutato in funzione delle dimensioni dell’input con
riferimento al caso peggiore, cioè quello in cui l’esecuzione impiega più tempo. Dovremo
quindi di volta in volta individuare qual’è il caso peggiore per quell’algoritmo, e valutare
come si comporta l’algoritmo su questo input.
Nel caso dell’esempio considerato, il caso peggiore è quello in cui l’elemento cercato
non è contenuto nell’archivio, per cui l’algoritmo di ricerca esaustiva effettua n confronti,
e diremo quindi che l’algoritmo ha un costo proporzionale ad n.
Vogliamo formalizzare quanto detto sopra. Diamo la seguente definizione.
Definizione 4.1 Un algoritmo ha complessità O(f (n)) (e diremo che l’algoritmo ha complessità O grande di f (n)) se esistono due costanti positive c ed n0 , indipendenti da n,
tali che il numero di istruzioni t(n) che devono essere eseguite nel caso peggiore con un
input di dimensione n verifica la seguente disuguaglianza
t(n) < c · f (n)
per ogni n > n0 .
Esempio: Se un algoritmo svolge un numero di istruzioni t(n) = 4n + 3, l’algoritmo è
O(f (n)) dove f (n) = n2 . Infatti basta scegliere c = 4 e n0 = 2. Si può anche osservare
che t(n) è anche O(n). Infatti basta prendere in questo caso c = 5 e n0 = 3.
Definizione 4.2 Diremo che un problema ha una delimitazione superiore (upper bound)
O(f (n)) alla sua complessità se esiste un algoritmo per la sua soluzione che ha complessità
O(f (n)).
Definizione 4.3 Diremo che un problema ha una delimitazione inferiore (lower bound)
O(f (n)) alla sua complessità se nessun algoritmo che risolve il problema può effettuare
su un generico input di taglia n meno di O(f (n)) operazioni elementari.
9
In generale questa funzione calcola quella che viene detta complessità asintotica di un
algoritmo, che ci dice come cresce il tempo di calcolo dell’algoritmo quando l’input cresce
di dimensione. Visto che si tratta di un’analisi più qualitativa che quantitativa, qualora
la funzione fosse una somma di diversi termini, considereremo solo quello “dominante”,
ossia quello che al crescere di n cresce più velocemente. Questo perché è sempre possibile,
con opportuni calcoli, fare assimilare i termini non dominanti dalla costante c. Il seguente
teorema afferma che se una funzione è un polinomio, allora la funzione è O grande del
termine di grado massimo, che è, infatti, il termine dominante.
Teorema 4.1 Sia A(n) = am nm + am−1 nm−1 + · · · + a1 n + a0 un polinomio di grado n.
Allora A(n) = O(nm ).
Dimostrazione:
|A(n)| ≤ |am |nm + |am−1 |nm−1 + · · · + |a1 |n + |a0 | ≤
≤ (|am | + |am−1 |/n + · · · + |a0 |/nm ) · nm ≤ (|am | + |am−1 | + · · · + |a0 |) · nm = cnm .
2
Questo teorema permette di dire che se un’algoritmo ha una complessità che è un polinomio di grado m, allora ha complessità O(nm ). Cioè si può non tenere conto dei termini
di grado inferiore, poiché sono termini che crescono con n meno velocemente di quello
“dominante”. Per lo stesso motivo si può non tenere conto delle costanti moltiplicative,
che vengono “assorbite” dalla costante c.
Abbiamo detto che questo criterio per la valutazione degli algoritmi non tiene conto
né delle costanti moltiplicative né dei termini di ordine inferiore. Si può però osservare
che se un programma fa 2n operazioni elementari è sicuramente diverso da uno che ne
fa 1000n. D’altra parte si può ossevare che per quanto le costanti moltiplicative siano
grandi, alla fine l’andamento qualitativo è determinato dalla funzione di n.
Se la funzione di complessità di un algoritmo è O(nm ), per qualche intero m, si dice
che ha complessità polinomiale. In particolare se m = 1, cioè l’algoritmo ha complessità
O(n) si dice che l’algoritmo ha complessità lineare. Se m = 2 si dice che l’algoritmo ha
complessità quadratica. Se la funzione di complessità di un algoritmo è O(log n), diremo
che l’algoritmo ha complessità logaritmica. Se la funzione di complessità di un algoritmo è
O(k n ), per qualche costante k > 1, diremo che ha complessità esponenziale. Un problema
per cui il migliore algoritmo possibile ha complessità esponenziale si dice intrattabile. Gli
algoritmi esponenziali richiedono un tale tempo di calcolo che nessun miglioramento futuro
della velocità dei calcolatori sequenziali produrrà mai un range più grande dell’insieme
dei problemi risolubili nella pratica.
10
log n
0
1
2
3
4
5
n
1
2
4
8
16
32
nlogn
0
2
8
24
64
160
n2
1
4
16
64
256
1024
n3
1
8
64
512
4096
32.768
2n
2
4
16
256
65.563
4.294.967.296
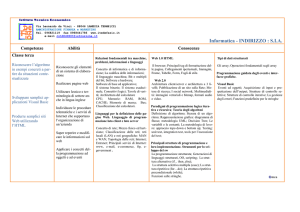
Figura 1: La tabella rappresenta i primi 5 valori delle funzioni indicate. Si noti come
passando da una funzione a quella superiore, il tasso di crescita diventa sempre maggiore
5
I linguaggi di programmazione
Un programma è un algoritmo, espresso in un determinato linguaggio formale, detto linguaggio di programmazione. I linguaggi formali si distinguono da quelli naturali in quanto
sono completamente definiti mediante regole esplicite, per cui è sempre possibile determinare la correttezza (grammaticale) di una proposizione; inoltre il significato di ogni frase
è sempre privo di ambiguità. Per contro i linguaggi naturali, che hanno delle ambiguità
intrinseche, hanno un potere espressivo più ampio dei linguaggi formali.
I linguaggi di programmazione sono un sottoinsieme di quelli formali. Essi possono
essere definiti come lo strumento che ci permette di comunicare al computer la sequenza
di operazione da effettuare per raggiungere un obiettivo prefissato.
Un’importante attività degli informatici è stata nel corso degli anni la definizione di
linguaggi per la codifica degli algoritmi, cioè i linguaggi che consentono di scrivere gli
algoritmi sotto forma di programmi che possono essere interpretati dal calcolatore, che ne
è l’esecutore. Una prima distinzione possiamo farla tra i linguaggi a basso e quelli ad alto
livello.
Ogni processore ha un proprio linguaggio che ad ogni stringa di bit fa corrispondere
una operazione elementare come il caricamento di un registro interno al processore o la
somma tra una cella di memoria e un registro. Questo tipo di linguaggio, detto linguaggio
macchina, essendo molto vicino alla logica del processore, risulta essere molto lontano dal
modo di ragionare dell’uomo, per cui utilizzarlo per la codifica di algoritmi comporta un
lavoro molto lungo e difficile. Agli albori dell’informatica, con l’avvento dei primi calcolatori, la programmazione consisteva nella traduzione minuziosa in linguaggio macchina
delle istruzioni, e la successione delle cifre binarie che codificava le istruzioni forniva il
programma, già pronto per essere eseguito dal calcolatore. Questo lavoro di traduzione
era chiamato codifica. La programmazione in linguaggio macchina portava comunque una
serie di problemi:
• questo metodo comportava un enorme lavoro da parte del programmatore, che era
11
generalmente un tecnico super specializzato, e inoltre la complessità del linguaggio
stesso impediva anche ai programmatori più esperti di scrivere programmi molto
complessi.
• Questo tipo di linguaggio portava i programmatori ad utilizzare certi tipi di “astuzie”
che erano spesso comprensibili solo da colui che aveva realizzato il programma, e
quindi difficilmente comprensibili ad un altro programmatore;
• per le stesse ragioni era difficilissimo in tali programmi, riconoscere e correggere gli
errori;
• questi linguaggi, essendo molto vicini alla logica del calcolatore, erano molto difficilmente trasportabili ad un altro tipo di calcolatore;
• infine il linguaggio macchina era molto lontano dal modo di ragionare dell’uomo,
nonché dai suoi mezzi espressivi (cioè il suo linguaggio naturale).
Tutte queste ragioni portarono gli studiosi del tempo a tentare di semplificare il modo di programmare, cercando di esprimere i programmi in un linguaggio più facilmente
comprensibile all’uomo. Un primo tentativo di semplificare il linguaggio di programmazione fu la creazione del linguaggio Assembler, in cui alcune istruzioni, che in linguaggio
macchina venivano espresse mediante delle sequenze di cifre binarie, venivano codificate
mediante delle parole chiave. Tuttavia la logica di base per la scrittura dei programmi
restava legata alla logica del calcolatore. L’Assembler quindi, pur permettendo una semplificazione del lavoro, costringeva a ragionare ancora in un modo strettamente legato a
quello del processore. Per cui in seguito si cercò di distaccarsi sempre piú dalla logica
dei processori arrivando cos ai cosiddetti linguaggi ad alto livello orientati non piú alla
macchina ma alla soluzione di problemi.
I linguaggi a basso livello furono accantonati quando, con l’invenzione del linguaggio
FORTRAN (FORmula TRANslation), venne per la prima volta introdotto un linguaggio ad alto livello, ossia più vicino alla logica dell’uomo e più lontano dalla logica
del calcolatore. I linguaggi ad alto livello si rivelarono subito più adatti a codificare gli
algoritmi oltre che molto più comprensibile dall’uomo. Inoltre il compito di tradurre il
programma nel linguaggio macchina è affidato alla macchina stessa mediante l’uso di un
particolare software, detto compilatore, che ha il compito da un lato di verificare la
correttezza sintattica del programma, e dall’altro di tradurre il programma nel linguaggio
macchina.
L’introduzione dei linguaggi di programmazione a basso livello ha portato dei grandissimi vantaggi:
• Molte più persone sono oggi in grado di programmare in questi linguaggi, dunque
si sono potuti realizzare programmi per risolvere problemi sempre più complessi
rispetto a quelli che si riuscivano ad affrontare con i linguaggi a basso livello;
12
• Questo sistema risulta portabile In quanto il programma risulta virtualmente indipendente dal processore o dalla macchina particolare in cui si sviluppa. Quindi un
cambiamento della macchina non stravolge drammaticamente il lavoro fatto;
• Il programma risulta più leggibile, nel senso che sia il programmatore originario
che un altro programmatore sono in grado di leggere, modificare o correggere senza
grosse difficoltà un programma già esistente.
Una volta verificata la maggiore efficacia dei linguaggi di programmazione ad alto
livello rispetto ai linguaggi a basso livello, tutto un filone della ricerca Informatica si
occupò di progettare vari tipi linguaggi di programmazione ad alto livello. In base al
modo di approcciarsi alla soluzione del problema, si parla di diversi paradigmi (dal greco
paradeigma=modello) di programmazione. Esistono due grosse classi di paradigmi di
programmazione: il paradigma dichiarativo e il paradigma procedurale o imperativo.
5.1
Il paradigma dichiarativo
Nel paradigma dichiarativo si elimina la fase di ricerca della strategia per la risoluzione
del problema (algoritmo) facendo in modo che la strategia risolutiva sia trovata dal programma stesso. Ci si concentra più sul “cosa” si deve risolvere piuttosto che sul “come”:
ecco perché i tempi di elaborazione possono essere piuttosto lunghi.
Esempio: Un programma di tipo dichiarativo per il Massimo Comun Divisore (MCD)
specificherà:
• La teoria dei numeri naturali e le definizioni di addizione, moltiplicazione etc.
• “cosa” vuole il problema, cioè la definizione di MCD. Per esempio “Il Massimo
Comun Divisore tra x e y è il massimo numero z tale che sia x che y divisi per z
danno come resto 0”.
• Il programma verificherà per ogni numero più piccolo di x e y se soddisfa la definizione.
I programmi dichiarativi sono in genere brevi, leggibili, verificabili e facilmente riutilizzabili. Sono molto vicini al metodo matematico di deduzione di predicati a partire da
certe premesse o assiomi. Tuttavia la programmazione dichiarativa ha un grande costo in
termini di efficienza. Per esempio nel caso del MCD l’interprete applicherà la definizione
sostituendo a una variabile z tutti i valori 1, 2, 3 . . . fino a trovare il valore di z che soddisfa
la definizione di Massimo Comun Divisore.
Nell’ambito dei paradigmi dichiarativi ritroviamo il paradigma logico, ossia quello
utilizzato nel linguaggio di programmazione PROLOG (PROgrammazione LOGica):
Il programma è considerato come la dimostrazione della verità di un‘asserzione.
13
• Si definisce una serie di assiomi o fatti elementari assunti come veri;
• I risultati vengono prodotti da un processo di calcolo deduttivo;
• Per definire un modello logico occorre definire: oggetti (domains), relazioni fra gli
oggetti (predicates), fatti e regole (clauses), obiettivi (goals);
I linguaggi logici risultano particolarmente adatti a risolvere problemi che riguardano
le relazioni fra varie entità. Il Prolog prende ispirazione dalla teoria matematica del calcolo
dei predicati del primo ordine.
Sempre nell’ambito del paradigma dichiarativo, la Programmazione Funzionale
trasforma invece il problema in una funzione, quindi l’OUTPUT sarà dato dal valore che
la funzione assume sul valore dell’INPUT. Nel linguaggio funzionale puro manca del tutto
l’assegnazione. Qui riveste particolare importanza la ricorsione e, come struttura dati, la
lista. Il linguaggio funzionale più utilizzato nella pratica è il LISP (LISt Processing)
che prende ispirazione dal lambda calcolo di Church, ed è stato utilizzato per esempio per
realizzare certi text editor come l’emacs.
5.2
Il Paradigma Imperativo e la Programmazione Strutturata
Il paradigma imperativo è caratterizzato dal fatto che, nella progettazione del programma, la fase fondamentale consiste nella ricerca di una strategia risolutiva per un problema
specifico, espressa mediante un algoritmo. Nel paradigma imperativo il programma costituito da una sequenza di istruzioni il cui effetto quello di modificare il contenuto
della memoria dell’elaboratore o di determinare le modalit di esecuzione di altre istruzioni; in questo modello assume un ruolo fondamentale l’istruzione di assegnazione. Sono
imperativi la maggior parte dei linguaggi piú diffusi (Pascal, Basic, Fortran, C, Cobol,
ecc.).
La Programmazione strutturata, alle cui regole si ispira il linguaggio Pascal, ma anche
la programmazione ad oggetti, è basata su dei principi fondamentali:
1. Scomposizione del problema in blocchi, ossia in problemi più semplici detti procedure.
2. Ogni blocco ha un solo punto di entrata e un solo punto di uscita.
3. Utilizzazione di solo 3 costrutti di controllo (sequenza, selezione, iterazione).
Ci si chiede se i principi della programmazione strutturata non siano troppo restrittivi. Per esempio ci si chiede se l’assenza del costrutto di salto incondizionato (GOTO),
utilizzato ampiamente in alcuni linguaggi di programmazione, che permette di passare
direttamente a una certa istruzione del programma, non limiti l’efficacia del linguaggio. Il
seguente importante teorema prova che tutto ciò che si può calcolare utilizzando paradigmi di programmazione più flessibili, può essere calcolato utilizzando la programmazione
strutturata.
14
Teorema 5.1 (di Böem - Jacopini) Un qualunque programma non strutturato può
essere realizzato utilizzando i soli costrutti di sequenza, selezione e iterazione.
5.3
Costrutto di sequenza
Il costrutto di sequenza consiste nell’elencare in maniera sequenziale le istruzioni che
devono essere eseguite. La sintassi di questo costrutto in Pascal è la seguente:
BEGIN
<istruzione 1>;
<istruzione 2>;
···
···
<istruzione n>;
END;
che equivale a dire: “Esegui la seguente sequenza di istruzioni in quest’ordine”.
5.4
Costrutto di selezione
Nel costrutto di selezione un’istruzione o una serie di istruzioni viene eseguita in dipendenza di una certa condizione. Il principale costrutto di selezione utilizzato in Pascal è il
seguente:
if < condizione > then
BEGIN
<sequenza di istruzioni 1>
END
else
BEGIN
<sequenza di istruzioni 2>;
END;
Questo costrutto significa: “se la <condizione> è vera allora esegui <sequenza di istruzioni 1>
altrimenti esegui <sequenza di istruzioni 2>.
In Pascal possiamo avere anche il seguente costrutto:
if <condizione> then
BEGIN
<sequenza di istruzioni>;
END;
che significa: “se la condizione è vera allora esegui istruzioni altrimenti passa all’istruzione
successiva”.
15
In Pascal esiste anche un costrutto di selezione che verifica allo stesso tempo diverse
condizioni:
case <espressione di controllo> of
V 1: BEGIN
<sequenza di istruzioni
END;
V 2: BEGIN
<sequenza di istruzioni
END;
...
V k: BEGIN
<sequenza di istruzioni
END;
else
BEGIN
<sequenza di istruzioni> {per
END;
1>
2>
k>
ogni valore non codificato}
I valori V k sono detti valori-chiave.
Questo costrutto significa: “Se il risultato dell’<espressione di controllo> è uno
dei valori chiave V i allora esegui le istruzioni corrispondenti <sequenza di istruzioni i>,
altrimenti esegui la <sequenza di istruzioni>”.
L’espressione di controllo deve essere una variabile intera o un carattere: non può
assumere valori reali. Tale costrutto non può essere utilizzato nei casi in cui la scelta è
fondata sulla valutazione di espressioni o il valore chiave è un certo intervallo: le grandezze
devono essere ben definite.
5.5
Costrutto di Iterazione
Nel costrutto di iterazione un’istruzione o una serie di istruzioni vengono ripetute tante
volte in relazione al verificarsi o meno ad una certa condizione che viene controllata all’inizio o alla fine di ogni ciclo. Affinché un costrutto di iterazione funzioni correttamente, le
condizioni devono essere sempre inizializzate e devono modificare il proprio valore durante
l’esecuzione del ciclo. Nei cicli condizionali (while e repeat) la condizione può essere o
una variabile booleana o un espressione valutabile in forma booleana (TRUE o FALSE). In
Pascal uno dei cicli condizionali è il ciclo while:
while <condizione> do
BEGIN
<sequenza di istruzioni>;
END;
16
che significa “continua ad eseguire la <sequenza di istruzioni> fintantoché la <condizione>
continua ad essere vera”.
In Pascal possiamo anche realizzare il ciclo condizionale mediante il costrutto repeat-until,
che ha la seguente sintassi:
repeat
<sequenza di istruzioni>
until <condizione>;
Che significa: “ripeti la <sequenza di istruzioni> fino a quando la <condizione>
diventa vera”.
Anche se le istruzioni sono più di una, i comandi BEGIN e END si possono omettere, in
quanto repeat e until svolgono loro il compito di parentesi.
Un altro costrutto di iterazione disponibile in Pascal è il ciclo for, che si può applicare
quando conosciamo a priori il numero di volte in cui il ciclo deve essere eseguito. In Pascal
ha la seguente sintassi:
for <variabile:= k to h> do
BEGIN
<sequenza di istruzioni>;
END;
che significa: “esegui h − k volte le istruzioni”.
Se h ≤ k allora il programma salta l’intera <sequenza di istruzioni>. La variabile deve essere un intero o un carattere (tra apici) o una variabile di tipo enumerativo.
Nelle dichiarazioni deve essere specificato l’intervallo in cui varia la variabile contatore.
i:=n..t; se al posto di to si scrive downto esegue il conto alla rovescia da k ad h.
5.6
Cicli equivalenti
I cicli while e repeat possono, con alcuni accorgimenti, essere utilizzati in maniera equivalente. Cosı̀ come sono definiti, essi differiscono dal fatto che mentre nel ciclo repeat-until
le istruzioni vengono eseguite almeno una volta, visto che la condizione viene verificata
alla fine, nel ciclo while la condizione viene testata all’inizio del ciclo, per cui se essa
non è vera la prima volta, il programma non eseguirà nemmeno una volta le istruzioni
del ciclo. Si noti inoltre che mentre nel ciclo while la condizione deve essere vera perchè
le istruzioni vengano eseguite, nel ciclo repeat-until l’istruzione deve risultare falsa per
riprendere ad eseguire da capo le istruzioni. Infine il ciclo for viene utilizzato quando
conosciano esattamente il numero di volte in cui le istruzioni devono essere eseguite. Esso
può essere simulato mediante i cicli while e repeat-until, ma non è vero il viceversa, cioè i cicli while e repeat-until non sempre possono essere simulati mediante un
17
ciclo FOR. Diamo ora uno schema di come si possono simulare alcune istruzioni di ciclo
condizionale mediante altre:
Il ciclo:
for i:=1 to n do
BEGIN
<sequenza di istruzioni>;
END;
è equivalente a:
i:=1; {inizializzazione del contatore i a 1}
while i<=n do
BEGIN
<sequenza di istruzioni>;
i:=i+1;
END;
oppure alle istruzioni:
i:=0; {inizializzazione del contatore i a 0}
repeat
<sequenza di istruzioni>;
i:=i+1;
until i=n;
Anche i cicli while e repeat-until possono essere resi equivalenti con particolari accorgimenti. Per esempio:
while <condizioni> DO
BEGIN
<sequenza di istruzioni>;
END;
è equivalente a:
if <condizioni> then {se la condizione è vera}
repeat
<sequenza di istruzioni>;
until not <condizioni>; {condizione falsa}
Il ciclo:
18
repeat
<sequenza di istruzioni>;
until <condizioni>
è equivalente a:
<sequenza di istruzioni>;
while not <condizioni> DO
BEGIN
<sequenza di istruzioni>;
END
6
Il Sistema Binario
Tutti i dati elaborati da un calcolatore vengono immagazzinati in memoria sotto forma di
parole binarie. La rappresentazione dell’informazione (o codifica) è l’assegnazione di una
stringa di simboli a ciascuno degli oggetti che vogliamo rappresentare. Abbiamo quindi
bisogno di un insieme finito di simboli, detto alfabeto. Generalmente considereremo un
alfabeto di due simboli (0 e 1) detto alfabeto binario. Se fissiamo un intero k, le possibili
sequenze distinte di lunghezza k costituite da due simboli sono in numero 2k . Infatti per
ciascuna posizione, il simbolo può essere scelto in due modi distinti, e otteniamo quindi
2k possibili combinazioni. Normalmente le parole binarie contenute nelle celle di memoria
sono di lunghezza 16 o 32 bits, quindi possiamo rappresentare fino a 216 o 232 diversi
elementi. Osserviamo che
28 = 216
216 = 65.536
232 = 4.294.967.296
Teorema 6.1 Sia b ∈ Z+ un intero non negativo. Ogni intero n > 1 può essere espresso
in maniera unica nella forma
n = am bm + am−1 bm−1 + · · · + a1 b + a0
dove m è un intero non negativo, 0 ≤ ai < b per i 6= m e 0 < am < b.
Questo teorema ci permette di rappresentare gli interi non negativi in qualunque base
b. Se infatti b è un intero non negativo, il numero n potrà essere rappresentato dalla
sequenza am am−1 · · · a1 a0 dove tutti gli ai sono minori di b. La sequenza am am−1 · · · a1 a0
sarà la rappresentazione numero n in base b. In particolare se b = 2, allora otteniamo
la rappresentazione binaria di n. Nel sistema binario quindi, ogni numero sarà espresso
19
con le sole cifre 0 e 1 (< b = 2). Il motivo per cui il sistema binario viene utilizzato
nei calcolatori è che un segnale binario si può facilmente ottenere mediante apertura e
chiusura dei circuiti. Se quindi ci viene dato un numero in forma binaria, per determinare
qual’è il suo valore in forma decimale, basta applicare la formula del teorema.
Ci interessa descrivere un algoritmo che ci permette di effettuare l’operazione contraria,
ossia dato un numero espresso in forma decimale, rappresentarlo in forma binaria.
6.1
Metodo delle Divisioni Successive
Tale metodo permette di esprimere un qualsiasi numero intero decimale n in forma binaria.
Il nostro obiettivo è quello di scrivere n come somma di potenze di 2. Il metodo generale
è quello di trovare la più grande potenza di 2 che si approssima per difetto ad n, sottrarla
al numero e iterare il procedimento sulla differenza fino ad arrivare al valore 1. Si scrive
quindi 1 in corrispondenza di ogni potenza di 2 presente e 0 per quelle che non figurano.
Esempio:
N = 149
149 − 128 = 21
21 − 16 = 5
5−4=1
27 = 128
24 = 16
22 = 4
20 = 1
quindi possiamo scrivere
n = 1 ∗ 27 + 0 ∗ 26 + 0 ∗ 25 + 1 ∗ 24 + 0 ∗ 23 + 1 ∗ 22 + 1 ∗ 20 .
Questo può essere espresso dicendo che (n)2 = 10010101.
Il metodo descritto è tuttavia algoritmicamente poco efficiente, poiché dobbiamo trovare,
provandole una per una, qual’è la potenza di 2 che più si approssima per difetto al numero
dato. Il metodo più frequentemente usato per determinare la rappresentazone binaria di
un numero è quello delle divisioni successive.
Consideriamo n = am bm +am−1 bm−1 +· · ·+a1 b+a0 che è un numero generico scritto in
base b. Se dividiamo il numero per b, utilizzando la distributività della divisione rispetto
alla somma, otteniamo:
a0
n
= am bm−1 + am−1 bm−2 + · · · + a1 +
b
b
Questo equivale a dire che am bm−1 + am−1 bm−2 + · · · + a1 è il quoziente e a0 è il resto della
divisione del numero per b. Questo significa che per ottenere il termine meno significativo
della rappresentazione in base b basta dividere il nostro numero (in base decimale) per
b e prendere il resto. Per ottenere il secondo termine meno significativo basta iterare il
procedimento sul quoziente. Il resto della divisione per b darà tale termine. Tale procedura
viene iterata finché non si arriva ad avere quoziente uguale a 1. Il numero in forma binaria
si ottiene leggendo l’ultimo quoziente (1) e tutti i resti letti dall’ultimo al primo.
20
Esempio: Sia n = 155
155 : 2 = 77 + 1
77 : 2 = 38 + 1
38 : 2 = 19 + 0
19 : 2 = 9 + 1
9:2=4+1
4:2=2+0
2:2=1+0
1
(155)2 = 10011011
6.2
Addizione fra due numeri binari
Per sommare due numeri espressi in forma binaria, si ricorre alla seguente tavola di
addizione per le cifre binarie
0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1 + 1 = 10
Per effettuare la somma di due numeri si agisce mediante il metodo di addizione noto
per i numeri decimali.
Esempio:
11001101 + 10101110 = 101111011
Si osservi che per sommare due numeri di taglia n si compiono circa 2n operazioni di accesso alla tavola di addizione (n per le somme delle cifre più eventualmente altre n somme
per i riporti). Diremo quindi che quest’algoritmo svolge O(n) operazioni elementari.
6.3
Moltiplicazione fra due numeri binari
Per moltiplicare 2 numeri di taglia n abbiamo bisogno di definire una tavola di moltiplicazione. Abbiamo che:
0 ∗ 0 = 0 ∗ 1 = 1 ∗ 0 = 0, 1 ∗ 1 = 1
Per quanto riguarda la moltiplicazione a più cifre ricorriamo al classico algoritmo della
moltiplicazione, per cui ogni cifra del secondo numero viene moltiplicata per il primo, e
infine i risultati, shiftati ciascuno di una posizione verso sinistra rispetto al precedente,
vengono sommati fra loro. Quindi per moltiplicare due numeri di taglia n, si ricorre n2
volte alla tavola di moltiplicazione, si compiono circa n SHIFT (spostamenti) e infine
si operano O(n2 ) somme. In totale otteniamo quindi che questo algoritmo svolge O(n2 )
operazioni elementari.
21
Osservazione: Esiste un algoritmo più sofisticato per la moltiplicazione di due numeri
binari che ha una complessità uguale a O(nlog 3 ).
Esercizi
1. Tradurre i seguenti numeri espressi in binario nei corrispondenti numeri decimali:
1001101, 1100110, 1010110, 11111, 111010, 1000001, 1101111, 1010000.
2. Tradurre i seguenti numeri espressi nel sistema decimale nei corrispondenti numeri
in sistema binario: 342, 118, 201, 74, 174, 131, 200, 100.
3. Effettuare le seguenti somme di numeri binari: 100100101 + 1001010, 11111111 +
1110101, 101001000 + 111100001, 1100110010 + 1010000100.
4. Effettuare i seguenti prodotti fra numeri binari: 10010×101, 10111×111, 1101×110,
11111 × 100.
6.4
Rappresentazione binaria degli interi relativi
Nei calcolatori è necessario dare una rappresentazione, oltre che degli interi positivi, anche
degli interi negativi. Esistono due possibili codifiche degli interi relativi (cioè sia positivi
che negativi). La prima è la rappresentazione con modulo e segno, che utilizza il primo
bit disponibile per la rappresentazione del segno (0 positivo e 1 negativo) e tutti gli altri
per la rappresentazione del modulo del numero. In tal modo, se abbiamo a disposizione
4 bit per la rappresentazione del numero, avremo che, per esempio, 3 sarà rappresentato
da 0011, mentre -3 sarà rappresentato da 1011.
Osserviamo che però questa rappresentazione crea ambiguità rispetto allo zero. Infatti
1000 e 0000 rappresentano entrambi lo zero. Questo può complicare il controllo delle
operazioni aritmetiche.
Per questo motivo spesso si adotta una rappresentazione diversa, che è la rappresentazione in complemento a due. In questa rappresentazione, se abbiamo a disposizione k bit
per rappresentare il nostro intero x, consideriamo la rappresentazione binaria di 2k + x, ed
eliminiamo la cifra più significativa (ossia quella più a sinistra). Per esempio, se abbiamo
a disposizione 4 bit e vogliamo rappresentare il numero 3, consideriamo la rappresentazione binaria di 16(= 24 ) + 3 = 19 che è uguale a 10011, ed eliminiamo la prima cifra,
ottenendo cosı̀ 0011 per la rappresentazione di 3 (che poi è esattamente corrispondente
alla rappresentazione binaria di 3). Stessa cosa se dobbiamo fare una rappresentazione di
−3: calcoliamo 16 − 3 = 13, calcoliamo la sua rappresentazione binaria 01101, ed eliminando la prima cifra, otteniamo 1101. Si noti che tutti i numeri positivi inizieranno per
0 mentre tutti i numeri negativi inizieranno per 1. Inoltre per ottenere l’opposto di un
numero occorre invertire tutti i bits del numero. Con questa codifica lo zero avrà un’unica
rappresentazione 0000 e potremo rappresentare i numeri interi da −2k−1 fino a 2k−1 − 1.
22
Vedremo in seguito come vengono rappresentati i numeri razionali e i numeri reali
all’interno del calcolatore.
6.5
Rappresentazione di dati non numerici
Oltre che i numeri, il calcolatore deve anche registrare dei dati non numerici, ossia le lettere dell’alfabeto e tutti gli altri caratteri (punteggiatura, parentesi, simboli speciali, etc.).
Per fare questo si sono stabiliti dei codici, che sono degli standard universali, per cui i
caratteri alfanumerici vengono codificati con particolari sequenze nell’alfabeto {0, 1}. Per
quanto riguarda i linguaggi occidentali, come l’italiano e l’inglese, il codice più frequentemente usato è il Codice ASCII (American Standard Code for Information Interchange)
che codifica i simboli utilizzando 7 bit (cioè vengono codificati 27 = 128 caratteri). Tuttavia questo codice non riesce, per esempio a rappresentare le lettere accentate, quindi
esistono delle versioni estese di codice ASCII (oggi più frequentemente usata) che utilizza
8 bit, con un’estensione a 256 caratteri. Simile a questa versione estesa del codice ASCII
è il codice EBCDIC (Extended Binary-Coded Decimal Interchange Code) sviluppato da
IBM e che fa uso, anch’esso di 8 bit. Tuttavia 8 bit non sono sufficienti a rappresentare i
caratteri di varie lingue del mondo (i caratteri greci, i caratteri cirillici, i caratteri arabi,
etc). Per questo è stato inventato un tipo di codice, chiamato UNICODE, basato su successioni di 16 bit, in grado quindi di codificare 216 = 65535 diversi caratteri. Per facilitare
il passaggio da ASCII a UNICODE, i primi 128 caratteri del codice UNICODE sono gli
stessi del codice ASCII.
23