Cenni di Matematica e Fisica

Fondamenti e Concetti della Fisica
Contemporanea
Cenni di Matematica e Fisica
Roberto Casalbuoni
Dipartimento di Fisica, Università di Firenze
Sezione INFN, Firenze
Istituto di Fisica Teorica Galileo Galilei, Arcetri, Firenze
OpenLab, Universita’ di Firenze
Appunti delle lezioni tenute all’Universita’ di Firenze nell’a.a. 2011/2012
nell’ambito della
Laurea Magistrale in Logica, Filosofia e Storia della Scienza.
Indice
Indice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1 Cenni di matematica
1.1 Funzioni . . . . . . . . . . . . . . . . . . .
1.2 Trigonometria . . . . . . . . . . . . . . . .
1.3 I limiti . . . . . . . . . . . . . . . . . . . .
1.4 Le derivate . . . . . . . . . . . . . . . . .
1.4.1 Equazioni differenziali e formula di
1.4.2 Funzioni di piu’ variabili . . . . . .
1.5 Gli integrali . . . . . . . . . . . . . . . . .
1.6 Numeri complessi . . . . . . . . . . . . . .
1.7 Le matrici . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Cenni di fisica
2.1 Introduzione . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 I postulati della meccanica classica . . . . . . . . . . . . . . .
2.3 Onde . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.1 Descrizione delle onde . . . . . . . . . . . . . . . . . .
2.3.2 L’interferenza . . . . . . . . . . . . . . . . . . . . . . .
2.3.3 Il meccanismo della visione . . . . . . . . . . . . . . .
2.4 Gli inizi della meccanica quantistica . . . . . . . . . . . . . .
2.4.1 Il corpo nero . . . . . . . . . . . . . . . . . . . . . . .
2.4.2 Einstein e i fotoni . . . . . . . . . . . . . . . . . . . .
2.4.3 Il problema atomico . . . . . . . . . . . . . . . . . . .
2.4.4 La meccanica delle onde e quella delle matrici . . . . .
2.4.5 Il significato probabilistico della funzione d’onda . . .
2.4.6 Il principio di indeterminazione . . . . . . . . . . . . .
2.4.7 Equivalenza della meccanica ondulatoria (Schrödinger)
canica delle matrici (Heisenberg) . . . . . . . . . . . .
2.5 L’esperimento di interferenza di Young . . . . . . . . . . . . .
2.6 L’esperimento di Stern e Gerlach . . . . . . . . . . . . . . . .
2.6.1 Analogia con la polarizzazione della luce . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
e
.
.
.
.
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
della
. . .
. . .
. . .
. . .
1
. . . .
. . . .
. . . .
. . . .
Taylor
. . . .
. . . .
. . . .
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
2
3
6
11
14
16
16
21
23
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
mec. . .
. . .
. . .
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
27
27
30
35
37
41
42
43
44
47
48
50
56
58
.
.
.
.
59
60
67
69
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Capitolo 1
Cenni di matematica
1.1
Funzioni
Una funzione e’ una regola per associare ad un oggetto un altro oggetto. L’oggetto da
cui si parte e’ detto l’argomento della funzione, quello di arrivo e’ il risultato prodotto
dalla funzione. L’insieme a cui appartiene l’argomento e’ detto il dominio della funzione.
Il risultato dell’applicazione di una funzione ad un argomento appartiene in genere ad un
insieme che e’ detto il codominio, ma l’insieme dei risultati e’ detto range della funzione. In generale, codominio e range non coincidono necessariamente. ma il range e’ un
sottoinsieme del codominio.
• Consideriamo f (x) = x2 . Questa funziona associa ad ogni argomento x appartenente ai reali (dominio) il suo quadrato che appartiene ai reali positivi (range). E’ da
osservare che la notazione f indica la trasformazione, mentre f (x) indica il risultato
della trasformazione f applicata all’argomento x. Nel caso specifico f sta per elevazione al quadrato. Mentre, per es. f (2) = 4 e’ il risultato di prendere il quadrato
di 2. Notiamo che il codominio e’ dato da tutti i numeri reali.
• Consideriamo la funzione g(x) = x2 con dominio sugli interi positivi. L’operazione
g coincide con l’operazione f ma il dominio di definizione e’ diverso. Quindi f e g
devono essere considerate funzioni diverse.
√
• Consideriamo h(x) = x. Perche’ questa funzione abbia senso il dominio deve
essere dato dai reali maggiori od uguali a zero. Il range sono i reali positivi, mentre
il codominio sono i numeri reali.
Qualche volta e’ utile considerare la composizione di due funzioni h(x) e j(x). La
composizione e’ una nuova funzioe k = h ◦ j definita calcolando prima j(x) e poi h(x).
Cioe’
k(x) = h ◦ j(x) = h(j(x))
(1.1)
Per esempio, se
h(x) = sin x,
2
j(x) = x2
(1.2)
si ha
k(x) = h ◦ j(x) = h(x2 ) = sin(x2 )
(1.3)
E’ da tener presente che se si inverte l’ordine delle funzioni il risultato e’ diverso. In questo
caso
j ◦ h(x) = j(sin x) = (sin x)2
(1.4)
Lo strumento fondamentale per lo studio dettagliato delle funzioni e’ il calcolo differenziale. L’idea, che nasce con Leibnitz e Newton, si basa sull’idea che qualunque tratto di
curva (vedi Figura 1.1), se preso su un intervallo sufficientemente piccolo, si puo’ assimilare
ad un segmento rettilineo
Figura 1.1: La figura in basso rappresenta la stessa curva disegnata in alto ma
nell’intervallo piu’ piccolo (1.4, 1.6). Come si vede, in questo intervallo puo’ essere
identificata con un segmento rettilineo.
Quindi l’idea e’ quella di andare a considerare quelle che si chiamano le proprieta’
locali delle funzioni per poi derivarne le proprieta’ generali. Prima pero’ di addentrarci
nel calcolo differenziale introduciamo alcune nozioni elementari di trigonometria.
1.2
Trigonometria
Consideriamo il cerchio di raggio uno di Figura 1.2 ed il triangolo descritto dai punti
P1 OQ1 . I rapporti dei cateti all’ipotenusa dipendono solo dal valore di θ1 e possiamo
3
y
I
II
P2
θ2
x2
P1
y1
y2
θ1 Q1
x1
O
x
III
IV
Figura 1.2: La figura illustra la definizione di seno e coseno per gli angoli θ1,2 .
quindi definire le seguenti funzioni dell’angolo θ1
sin θ1 =
P1 Q1
= y1 ,
OP1
cos θ1 =
OQ1
= x1
OP1
(1.5)
dove si e’ tenuto conto che OP1 = 1. In queste definizioni le coordinate x, y sono prese con
il loro segno algebrico. Dunque nel primo quadrante sono entrambe positive e cosi’ saranno
seno e coseno. Nel secondo quadrante x e’ negativo e quindi il seno e’ positivo mentre il
coseno e’ negativo. Questo caso e’ considerato nella Fig.1.2, come l’agolo θ2 .Analogamente
si possono considerare gli altri casi Nel III quadrante sono entrambi negativi, mentre nel
IV il coseno e’ positivo ed il seno negativo. Si trovano anche subito i seguenti valori del
seno e coseno per valori particolari degli angoli
sin 00 = 0,
cos 00 = 1,
sin 900 = 1,
cos 900 = 0,
1
sin 450 = cos 450 = √
2
(1.6)
per il teorema di Pitagora si ha
(P1 Q1 )2 + (OQ1 )2 = (OP1 )2 = 1
(1.7)
sin2 θ1 + cos2 θ1 = 1
(1.8)
da cui
Questa proprieta’ vale per qualunque valore dell’angolo e quindi le funzioni seno e coseno
non sono indipendenti tra loro.
Segue subito dalla definizione di seno e coseno (il punto P ritorna su se stesso dopo
un giro di 3600 ), ma anche guardando il grafico di Figura 1.3, che si tratta di funzioni
periodiche con un periodo di 3600 , cioe’
sin(θ + 3600 ) = sin θ,
cos(θ + 3600 ) = cos θ
4
(1.9)
1.0
0.5
50
100
150
200
250
300
350
-0.5
-1.0
Figura 1.3: Il grafico delle funzioni seno (linea continua) e coseno (linea tratteggiata)
tra 0 e 360 gradi.
Relazioni importanti sono le seguenti (che dimostreremo facendo uso dei numeri complessi)
sin(α + β) = sin α cos β + sin β cos α
cos(α + β) = cos α cos β − sin α sin β
(1.10)
Un’altra funzione trigonometrica spesso usata e’ la tangente definita come il rapporto tra
6
4
2
-200
100
-100
200
-2
-4
-6
Figura 1.4: La funzione trigonometrica tangente.
seno e coseno:
tan θ =
sin θ
cos θ
(1.11)
Si vede che questa funzione e’ periodica, con periodo 1800 come e’ chiaro dal suo grafico
in Fig. 1.4:
tan(θ + 180) = tan θ
(1.12)
5
Dalla Fig. 1.2 vediamo che la tangente dell’angolo θ1 e’ anche data da
tan θ1 =
y1
P1 Q1
=
OQ1
x1
(1.13)
In molti casi e’ conveniente misurare gli angoli in radianti. Per definire questa misura,
consideriamo la Figura 1.5. Allora si definisce il valore di α in radianti come il rapporto tra
l’arco AB ed il raggio OA. Per un cerchio di raggio 1 corrisponde alla lunghezza dell’arco
corrispondente.
La lunghezza dell’arco per un angolo giro vale 2π e quindi si ha la seguente corrispondenza tra i valori in gradi ed i valori radianti
3600 ⇔ 2π,
1800 ⇔ π,
900 ⇔
Piu’ precisamente
αradianti = αgradi
π
,
2
450 ⇔
π
4
π
180
(1.14)
(1.15)
B
α
O
A
Figura 1.5: La misura di un angolo in radianti.
1.3
I limiti
Supponiamo sia data una funzione f (x) ed un punto a sull’asse delle x. Quello che vogliamo
determinare e’ cosa succede alla f (x) quando x e’ molto vicino ma non uguale ad a.
Consideriamo per esempio la seguente funzione con dominio tutto l’asse reale eccetto il
punto x = 2
f (x) = 3x − 1,
per x 6= 2
(1.16)
Ovviamente non ha senso dire che f (2) = 5 dato che questa funzione non e’ definita in quel
punto1 . Posssiamo pero’ domandarci che valore assume la funzione quando siamo molto,
1
Vedremo in seguito che casi di questo tipo, sebbene appaiono molto artificiali, li incontreremo
spesso
6
molto vicini a 2. Per capire il punto costruiamo due tabelle, la prima in cui partiamo
da valori di x < 2 calcolando il corrispondente valore della f ed un’altra analoga ma per
valori decrescenti di x
x
1 1.5 1.9 1.99 1.999
(1.17)
f(x) 2 3.5 4.7 4.97 4.997
x
f(x)
3
8
2.5
6.5
2.1
5.3
2.01
5.03
2.001
5.003
(1.18)
Vediamo che avvicinandosi a 2 da entrambe le parti il risultato si avvicina sempre piu’ a 5.
Partendo da valori inferiori a 2 la sequenza superiore tende a 5 per valori inferiori, mentre
per valori superiori a 2 la seuqnza tende a 5 per valori maggiori a 5. Dunque abbiamo
due successioni numeriche, una che tende a 5 per valori inferiori a 2 ed una che ci tende
per valori superiori. Questo e’ il modo usuale con il quale si definiscono, per esempio, i
numeri reali, tramite due successioni che approssimano il numero una per valori superiori
e l’altra per valori inferiori. Dunque diremo che
lim f (x) = 5
(1.19)
x→2
Dunque, questa procedura ci permette di dare un senso a qualcosa che a priori non e’
definito.
In questa definizione di limite abbiamo considerato la convergenza ad un determinato
valore sia partendo da valori minori di x che maggiori rispetto al punto limite. Possiamo
pero’ definire anche un limite da destra e uno da sinistra. Indicheremo il limite fatto
da destra o da sinistra con i due simboli limx→a± . Consideriamo, per esempio, la curva
6
4
2
-2
1
-1
2
3
4
Figura 1.6: Nel punto x = 3. che non appartiene al dominio della curva in figura,
il limite destro ed il limite sinistro non coincidono.
di Fig. 1.6 che non e’ definita per x = 3. Possiamo pero’ definire il limite destro e quello
sinistro che sono rispettivemente:
lim f (x) = 6,
lim f (x) = 2
x→3−
x→3+
7
(1.20)
Ovviamente, se il limite destro e quello sinistro esistono ma non coincidono il limite tout
court (cioe’ quello definito in precedenza) non esiste.
In molti casi e’ interessante conoscere il comportamento della funzione per grandi valori
di x. In questo caso definiamo il limite per x → ±∞ e scriveremo
lim f (x) = L±
x→±∞
(1.21)
Dove si intende che prendendo x sempre piu’ grande in valore assoluto, se x > 0, allora il
valore della funzione diventa sempre piu’ vicino a L+ o a L− quando x < 0.
Facciamo alcuni esempi meno banali. Consideriamo la seguente funzione
f (x) =
x2 − 3x + 2
x−2
(1.22)
e notiamo che questa funzione e’ definita ovunque eccetto in x = 2 dove il denominatore
si annulla. Se ne consideriamo il limite in un qualunque punto diverso da x = 2 possiamo
semplicemente sostituire il valore di x dentro la funzione e calcolare il risultato. Per
esempio
(−1)2 − 3(−1) + 2
= −2
(1.23)
lim
x→−1
−1 − 2
Ma per x = 2 non possiamo seguire questa strada. In generale occorre seguire la procedura
che abbiamo visto prima,cioe’ studiare cosa succede quando x si avvicina sempre piu’ a 2
ma senza uguagliarlo. In molti casi ci sono dei trucchi che possiamo adottare. Nel caso in
esame si puo’ notare che anche il numeratore si annulla per x = 2. Questo significa che si
puo’ fattorizzare il numeratore estraendo il fattore x − 2. Infatti avremo
x2 − 3x + 2
(x − 2)(x − 1)
= lim
= lim (x − 1) = 1
x→2
x→2
x→2
x−2
x−2
lim
(1.24)
Dato che nell’ultimo passaggio, l’espressione che risulta dopo la divisione tra i due polinomi
al numeratore ed al denominatore e’ ben definita, e quindi possiamo calcolare il limite
semplicemente sostituendo il valore di x. Notiamo che la f (x) e (x − 1) non sono la stessa
funzione, dato che la f (x) e’ definita su tutto l’asse reale escludendo il punto x = 2, mentre
la seconda funzione e’ definita ovunque. Ma l’osservazione cruciale e’ che le due funzioni
sono uguali in tutti gli altri punti. Questo fatto ci permette di calcolare in modo semplice
il limite della f (x) nel punto in cui non e’ ben definita.
Se consideriamo il rapporto di due polinomi e gli zeri del denominatore non coincidono
con zeri del numeratore, il limite in questi punti tendera’ a ±∞ a seconda del segno della
funzione per grandi valori di |x|.
Intuitivamente diciamo che una curva e’ continua se la possiamo disegnare senza alzare
la penna dal foglio. Ci sono pero’ funzioni come 1/x (vedi Fig. 1.7) che vanno a +∞ per
x → 0+ e a −∞ per x → 0− che non godono di questa proprieta’ perche’ x = 0 non sta
nel dominio ed inoltre il limite destro ed il limite sinistro non coincidono.
Diremo dunque che una funzione e’ continua nel punto x = a se a e’ nel dominio della
funzione e se
lim f (x) = f (a)
(1.25)
x→a
8
2
1
-4
2
-2
4
-1
-2
Figura 1.7: Il grafico di 1/x.
Ovviamente questa scrittura contiene implicitamente il fatto che i limiti destro e sinistro
esistono e coincidono.
Un limite che e’ spesso utile considerare e’ il seguente:
sin x
=1
x→0 x
lim
(1.26)
Senza entrare in una dimostrazione formale facciamo vedere graficamente in Fig 1.8, come
sin x e x vadano a zero nello stesso modo quando x → 0
1.5
1.0
0.5
-1.5
-1.0
0.5
-0.5
1.0
1.5
-0.5
-1.0
-1.5
Figura 1.8: I grafici di sin x e x in vicinanza di x = 0.
Tramite la nozione di limite siamo adesso in grado di definire un particolare numero di
grandissima rilevanza nella matematica. Stiamo parlando del numero di Eulero che e’ un
numero trascendente (cioe’ non esiste equazione algebrica che lo ammetta come soluzione)
9
la cui rappresentazione decimale (ovviamente infinita, come π) e’ data da
e = 2.71828182845904523536028.....
(1.27)
La definizione rigorosa di e e’ la seguente
e = lim
n→∞
1+
1
n
n
(1.28)
Questa espressione ha il significato che si devono calcolare i termini della successione
e1 , e2 , · · · ....
(1.29)
A questo punto piu’ grande e’ il valore di n che si considera, tanto piu’ il termine en della
successione en definita da
1 n
en = 1 +
(1.30)
n
si avvicina ad e. Per esempio si ha
e1 = 2,
e2 = 2.25,
e3 = 2.37, · · · e10 = 2.59374,
e1000 = 2.71692, · · ·
(1.31)
Scegliendo n sufficientemente grande possiamo calcolare e con la precisione che si vuole
(anche se questo non e’ il metodo piu’ efficiente).
Supponiamo adesso di voler calcolare una potenza di e,
a
1 n
a m
1 an
a
e = lim
1+
(1.32)
= lim 1 +
= lim 1 +
n→∞
m→∞
n→∞
n
n
m
dove abbiamo sotituito ad n la quantita’ m/a. Infatti fare il limite per n → ∞ o m → ∞
non fa differenza.
Ricordiamo qui anche la definizione di logaritmo. Se abbiamo una equazione del tipo
ax = b,
a, b > 0
(1.33)
con a e b noti, il valore di x per cui questa e’ soddisfatta si chiama il logaritmo di b in
base a e si scrive
x = loga b
(1.34)
Quindi, per definizione
aloga b = b
(1.35)
Ricordiamo alcune proprieta’ del logaritmo
b
= loga b − loga c,
loga (bc) = loga b + logb c,
loga
c
loga (br ) = r loga b
(1.36)
Jnoltre
loga 1 = 0,
loga a = 1,
10
loga (ax ) = x
(1.37)
Esiste anche un modo semplice per cambiare la base dei logaritmi in cui si lavora. Precisamente, i logaritmi di uno stesso numero in due basi diverse sono correlati da
loga x =
logc x
logc a
(1.38)
Ovviamente la scelta della base per i logaritmi e’ completamente arbitraria. Quando
si usano per calcoli numerici una base molto conveniente e’ la base 10, ma quando si voglia
una base comoda per sviluppi matematici, questa e’ la base e, cioe’ si sceglie come base il
numero di Eulero. I logaritmi in base e sono anche detti logaritmi naturali. I logaritmi
naturali hanno una scrittura particolare che non indica la base stessa2 :
loge a ≡ ln a
(1.39)
In particolare, per i logaritmi naturali valgono le seguenti regole
eln x = x,
ln(xy) = ln x + ln y,
1.4
ln(ex ) = x, ln 1 = 0
x
= ln x − ln y, ln xy = y ln x
ln
y
(1.40)
(1.41)
Le derivate
Se vogliamo definire la velocita’ media di una automobile dobbiamo prendere la distanza
percorsa in un dato tempo e dividerla per il tempo impiegato, cioe’
velocita′ media =
distanza
tempo
(1.42)
Un modo per misurare la distanza e’ considerare i segnali chilometrici. Se ad una dato
istante passiamo da un dato segnale chilometrico, diciamo che la nostra posizione e’ quella
indicata dal segnale. In pratica stiamo definendo una funzione tale che quando l’argomento
e’ il tempo che corrisponde al passaggio da un dato segnale, assume un valore numerico
pari al valore dei chilometri indicati. Se chiamiamo questa funzione posizione, potremo
scrivere la distanza tra due segnali come
posizione(t2 ) − posizione(t1 ) = distanza tra i due segnali
(1.43)
dove t1 e t2 sono gli istanti di tempo nei quali passiamo al primo ed al secondo segnale.
Se immaginiamo di avere una distribuzione di segnali in tutti i punti della strada che
stiamo percorrendo, possiamo definire una funzione che ad ogni istante ci segnala la nostra
posizione sulla strada in relazione all’istante considerato. Chiamando questa funzione con
s(t) possiamo definire la velocita’ media come
v̄ =
s(t2 ) − s(t1 )
t2 − t1
2
(1.44)
Ma qualvolta, per abuso di notazioni, scriveremo ln a nella forma log a. Cioe’, ogni volta che
non si indichi esplicitamente la base si intende che il logaritmo e’ in base e
11
dove t1 e t2 sono gli istanti tra i quali vogliamo calcolare la velocita’ media.
Supponiamo adesso di voler determinare la velocita’ ad ogni istante t, cioe’ quello che
in pratica fa un contachilometri. A questo scopo fissiamo l’istante t al quale vogliamo
definire la velocita’. Poi prendiamo un altro istante t′ e calcoliamo la velocita’ media
prendendo t′ sempre piu’ vicino a t. Quello che stiamo facendo e’ di definire la velocita’
istantanea come il limite
s(t′ ) − s(t)
(1.45)
v = lim
t′ →t
t′ − t
Ovviamente e’ necessario il concetto di limite in questa definizione perche’ il rapporto
che definisce la velocita’ media non e’ definito quando i due istanti considerati coincidono.
Una maniera piu’ illuminante per definire la velocita’ istantanea (velocita’ tout court) e’
quello di considerare t′ = t + ∆t e poi prendere il limite per ∆t che tende a zero
s(t + ∆t) − s(t)
∆t→0
∆t
v = lim
(1.46)
Si dice anche che la velocita’ e’ il limite del rapporto incrementale, o la derivata di s(t),
ed il risultato del limite viene rappresentato in vari modi. Per esempio
v=
ds(t)
= ṡ(t)
dt
(1.47)
sono notazione equivalenti. La seconda espressione ricorda il fatto che la derivata e’ il
limite del rapporto tra due variazione, la variazione della posizione e la variazione del
tempo. Infatti potremmo scrivere
∆s = s(t + ∆t) − s(t)
(1.48)
che rappresenta la variazione di posizione nel passare dal tempo t al tempo t+∆t e scrivere
∆s
ds(t)
= lim
∆t→0 ∆t
dt
(1.49)
Dopo questa premessa, consideriamo una generica funzione f (x) e definiamone la
derivata come il limite del rapporto incrementale
f (x + ∆x) − f (x)
df (x)
≡ f ′ (x) = lim
∆x→0
dx
∆x
(1.50)
La derivata ha un semplice significato geometrico. Consideriamo la Fig. 1.9. Il rapporto
incrementale e’ il rapporto dei due cateti ∆f (x) e ∆x del triangolo rettangolo che ha
per ipotenusa la linea tratteggiata che passa per i punti (x + ∆x, f (x + ∆x) e (x, f (x).
Dunque e’ la tangente dell’angolo che l’ipotenusa forma al vertice f (x) con il catetoo,
in altri termini, la pendenza dell’ipotenusa. Quando facciamo tendere ∆x a zero, questa
ipotenusa tende a diventare la tangente alla curva nel punto di coordinate (x, f (x). Questa
osservazione permettere di capire molto semplicemente quanto vale la derivata guardando
il grafico della funzione.
12
f(x)
f(x + ∆ x)
∆ f(x)
f(x)
x+ ∆ x
x
x
Figura 1.9: Illustrazione del significato geometrico della derivata.
Facciamo alcuni esempi: consideriamo f (x) = c con c costante indipendente da x,
allora
df (x)
c−c
= lim
=0
(1.51)
∆x→0 ∆x
dx
Quindi la derivata di una costante e’ zero. Esprime semplicemente il fatto che una costante
non cambia. Od anche osservando che il grafico che corrispondente a f (x) = c e’ una retta
orizzontale nel piano (x, f (x)) che passa per il punto f (x) = c. Ma una retta orizzontale
ha pendenza zero.
Se prendiamo f (x) = x
dx
(x + ∆x) − x
= lim
=1
∆x→0
dx
∆x
(1.52)
dx2
2x∆x + ∆2
(x + ∆x)2 − x2
= lim
=
= 2x + ∆x
∆x→0
dx
∆x
∆x
(1.53)
Infine consideriamo f (x) = x2
Nel limite in cui ∆x va a zero si trova
dx2
= 2x
dx
(1.54)
Riportiamo di seguito una tavola con le derivate delle funzioni piu’ importanti
f (x)
c
xn
sin(cx)
cos(cx)
ecx
ln x
df (x)/dx
0
nxn−1
c cos(cx)
−c sin(cx)
cecx
1/x
13
(1.55)
Tavola 1 - Una tavola di derivate. In queste espressioni c e’ una costante.
Una regola importante e’ quella che serve per calcolare la derivata di un prodotto. Si
ha
f (x + ∆x)g(x + ∆x) − f (x)g(x)
=
∆x→0
∆x
f (x + ∆x)g(x + ∆x) − f (x + ∆x)g(x) + f (x + ∆x)g(x) − f (x)g(x)
lim
(1.56)
∆x→0
∆x
(f (x)g(x))′ = lim
dove nell’ultimo passaggio abbiamo aggiunto e levato f (x + ∆x)g(x). Possiamo riscrivere
f (x + ∆x)(g(x + ∆x) − g(x)) + (f (x + ∆x) − f (x))g(x)
∆x→0
∆x
(f (x)g(x))′ = lim
(1.57)
Dato che nel limite f (x + ∆x) tende a f (x) si trova
(f (x)g(x))′ = f (x)g′ (x) + f ′ (x)g(x)
(1.58)
Infine consideriamo la derivata di una funzione di funzione, cioe’ di un funzione f (x) dove
a sua volta x e’ una funziona di un’altra variabile y, cioe’ f (x(y)). Ci si chiede quale sia
la derivata della funzione f rispetto ad y. Si ha
df (x) df (x(y))
dx(y)
=
dy
dx x=x(y) dy
(1.59)
Supponiamo, per esempio, di avere la funzione f (y) = sin(y 3 ). Per calcolare la sua
derivata introduciamo x = y 3 . Dunque
d sin x dy 3
df (x(y))
=
= cos x 3 3y 2 = 3y 2 cos(y 3 )
3
dy
dx x=y dy
x=y
(1.60)
Le derivate di ordine piu’ alte si definiscono per ricorrenza. La derivata seconda e’ la
derivata della derivata prima, ecc. La derivata di ordine n viene indicata con uno dei
seguenti simboli
dn f (x)
f (n) (x) =
(1.61)
dxn
1.4.1
Equazioni differenziali e formula di Taylor
Consideriamo una equazione differenziale del primo ordine del tipo:
df (x)
+ h(x)f (x) = g(x)
dx
(1.62)
dove h(x) e g(x) sono funzioni note e f (x) e’ la funzione incognita. Un teorema fondamentale sulle equazioni differenziali dice che: se assegniamo il valore di f (x) in un punto,
l’equazione ha una ed una sola soluzione.
14
L’idea della dimostrazione e’ molto semplice. Consideriamo la definizione di derivata
(1.50). Se la quantita’ ∆x e’ sufficientemente piccola, possiamo approssimare la derivata
della funzione f (x) nel punto x, con il relativo rapporto incrementale
df (x)
f (x + ∆x) − f (x)
≈
dx
∆x
(1.63)
Ma questa relazione puo’ anche essere usata per calcolare approssimativamente la f (x +
∆x) in funzione della f (x) e della sua derivata nello stesso punto:
f (x + ∆x) ≈ f (x) + ∆x
df (x)
dx
Data allora la funzione in un punto x0 , la possiamo calcolare in un punto vicino
df (x) f (x0 + ∆x) ≈ f (x0 ) + ∆x
= f (x0 ) + ∆x (g(x0 ) − h(x0 )f (x0 ))
dx x=x0
(1.64)
(1.65)
dove abbiamo usato l’equazione differenziale per riesprimere la derivata di f (x) in x0 in
termini di f (x0 ). Adesso il secondo membro e’ noto e quindi conosciamo f (x0 + ∆x).
Possiamo poi procedere analogamente per calcolare la f nel punto x0 + 2∆x0 )
df (x) (1.66)
f (x0 + 2∆x) = f (x0 + ∆x) + ∆x
dx x=x0 +∆x
Dato che dal calcolo precedente abbiamo determinato f (x0 +∆x), possiamo riesprimere
la derivata nel punto x0 + ∆x usando l’equazione differenziale dove compaiono adesso
tutte quantita’ note. Cosi procedendo e’ possibile determinare la f (x) in tutti i punti.
Naturalmente questa procedura e’ tanto piu’ corretta quanto piu’ piccolo si [rende ∆x.
Una procedura di questo tipo, o sue variazioni, viene usata per risolvere, o integrare,
numericamente un’equazione differenziale. Questa procedura e’ facilmente implementabile
in un calcolatore elettronico.
In genere, l’errore che si fa in questa approssimazione e’ di ordine (∆x)2 . Per esempio se ∆x ≈ 0.1, l’errore e’ di ordine 10−2 . Usando questo risultato si puo’ calcolare
l’approssimazione a ex0 nel seguente modo
ex0 +∆x ≈ ex0 + ∆xex0 = ex0 (1 + ∆x)
(1.67)
Il valore della funzione in un punto, che serve per risolvere l’equazione differenziale, viene
anche detto costante d’integrazione.
La formula (1.65) e’ un caso particolare di una formula piu’ generale che si chiama
formula di Taylor che permette di calcolare il valore di una funzione in un punto se si
conoscono le prime N derivate
f (x) ≈ f (a) + (x − a)f ′ (a) +
1
1
(x − a)2 f ′′ (a) + · · ·
f (N −1) (a)
2!
(N − 1)!
dove
f (N ) (a) ≡
dN f (x) dxN x=a
15
(1.68)
(1.69)
La correzione a questa espressione e’ in genere di ordine (x − a)N . Per esempio, se ci
limitiamo sino al termine con la derivata terza, e se x − a = 0.1, l’errore che facciamo e’
di ordine (10−1 )4 = 10−4 = 0.0001. Sotto certe ipotesi possiamo prendere il limite per
N → ∞ di questa espressione e trovare una rappresentazione esatta (detta sviluppo in
serie) della funzione f (x)
∞
X
1
(x − a)n f (n) (a)
(1.70)
f (x) =
n!
n=0
ex
Se consideriamo
e sviluppiamo in serie per a = 0, dato che la derivata prima e’
uguale all’esponenziale di partenza, tutte le derivate sono uguali all’esponenziale e se le
calcoliamo a x − 0 si trova 1. Il risultato e’ che l’esponenziale ammette il seguente sviluppo
in serie
∞
X
1 2
xn
1 n
x
e = 1 + x + x + ··· + x + ··· =
(1.71)
2!
n!
n!
n=0
Questi risultati si possono facilmente generalizzare al caso di equazioni differenziali di
ordine piu’ elevato, cioe’ ad equazioni che coinvolgano la derivata ennesima di una funzione.
In questo caso per avere un’unica soluzione occorre assegnare n costanti d’integrazione che,
per esempio, possono essere scelte come il valore della funzione e delle sue derivate sino
all’ordine (N − 1) in un punto. Vedremo in seguito alcuni esempi.
1.4.2
Funzioni di piu’ variabili
Nel caso di funzioni di piu’ variabili si possono definire le derivate rispetto alle singole
variabili. In questo caso si parla di derivate parziali. Per esempio, se si ha una funzione
f (x, y) la sua derivata parziale rispetto ad x e’ definita da
∂f (x, y)
f (x + ∆x, y) − f (x, y)
= lim
∆x→0
∂x
∆x
(1.72)
f (x, y + ∆y) − f (x, y)
∂f (x, y)
= lim
∆y→0
∂y
∆y
(1.73)
ed analogamente
Quindi, quando si esegue una derivata parziale rispetto ad una variabile, le altre devono
essere tenute ferme. Per esempio
∂(x3 y 2 )
= 3x2 y 2 ,
∂x
1.5
∂(x3 y 2 )
= 2x3 y
∂y
(1.74)
Gli integrali
Ci sono due tipi di integrali, il cosi detto integrale indefinito e quello definito. L’integrale
indefinito e’ l’operazione inversa della derivata. Cioe’ data un funzione f (x), il suo integrale
indefinito
Z
F (x) = f (x)dx
(1.75)
16
e’ quella funzione F (x) tale che la sua derivata e’ f (x). F (x) e’ anche detta una primitiva
di f (x)
dF (x)
= f (x)
(1.76)
dx
Quindi per calcolare l’integrale di una funzione elementare come quelle di Tavola 1 basta
leggere la tavola stessa in ordine inverso. L’integrale indefinito dipende da una costante
arbitraria, dato che la derivata di una costante e’ nulla. Per esempio, l’integrale di x sara’
Z
x2
x dx =
+c
(1.77)
2
Troviamo cosi la seguente tavola di integrali indefiniti
R
f (x)
f (x) dx
n
n+1
x
x
/(n + 1) + cost
cos(cx)
sin(cx)/c + cost
sin(cx) − cos(cx)/c + cost
ecx
ecx /c + cost
1/x
ln x + cost
(1.78)
Tavola 2 - Una tavola di integrali. In queste espressioni c e’ una costante.
Chiaramente il concetto di integrale indefinito e’ utile per risolvere una equazione
differenziale.
Vediamo alcuni esempi.
Moto con accelerazione costante
In questo caso la derivata della velocita’, cioe’ l’accelerazione e’ costante, quindi
Z
Z
dv
dv
= a → v(t) =
dt = adt = at + costante
dt
dt
(1.79)
con a una costante indipendente dal tempo. Pertanto
v(t) = at + costante
(1.80)
Come possiamo determinare la costante? Se assegniamo la velocita’ v0 al tempo t0 ,
dovremo avere
v(t0 ) = v0 = at0 + costante
(1.81)
Possiamo ricavare la costante da questa relazione
costante = v0 − at0
(1.82)
v(t) = at + v0 − at0
(1.83)
e sostituendo
17
da cui
v(t) = v0 + a(t − t0 )
(1.84)
Se ci chiediamo come varia la posizione della particella nel caso in esame, dovremo risolvere
l’equazione
ds(t)
= v(t) = v0 + a(t − t0 )
(1.85)
dt
In questa equazione abbiamo a secondo membro un termine costante ed uno lineare in t.
In entrambi i casi si calcolano agevolmente le primitive con il risultato
1
s(t) = (v0 − at0 )t + at2 + costante
2
(1.86)
Se conosciamo la posizione al tempo t0 , s0 = s(t0 ), possiamo determinare la costante
risolvendo
Dunque
e sostituendo
1
1
s0 = (v0 − at0 )t0 + at20 + costante = v0 t0 − at20 + costante
2
2
(1.87)
1
costante = s0 − v0 t0 + at20
2
(1.88)
1
1
s(t) = (v0 − at0 )t + at2 + s0 − v0 t0 + at20
2
2
(1.89)
da cui
1
(1.90)
s(t) = s0 + v0 (t − t0 ) + a(t − t0 )2
2
Un esempio meno banale e’ il moto di una molla. In questo caso, dalla legge di Newton,
F = ma e dal fatto che per spiccoli spostamente, la molla tende a ritornare alla posizione
di equilibrio con una forza proporzionale allo spostamento, F = −kx, si ha
m
d2 x(t)
= −kx(t)
dt
(1.91)
Occorre dunque trovare una funzione che derivata due volte e’ proporzionale a se stessa.
Vediamo dalle nostre tavole che le funzioni trigonometriche seno e coseno godono entrambe
di questa proprieta’. Segue immediatamente che la soluzione e’ data da
x(t) = A cos ωt + B sin ωt,
ω2 =
k
m
(1.92)
Dove le costanti A e B sono legate alle condizioni iniziali. Per esempio, se diamo a t = 0
la posizione e la velocita’, avremo
x0 = x(0) = A
(1.93)
v0 = v(0) = [−ωA sin ωt + ωB cos ωt]t=0 = ωB
(1.94)
e
18
Quindi
v(0)
sin ωt
(1.95)
ω
L’integrale definito e’ invece introdotto nel seguente modo. Consideriamo una funzione
f (x) nell’intervallo (a, b), allora il suo integrale definito tra a e b, e che viene indicato con
Z b
f (x)dx
(1.96)
x(t) = x(0) cos ωt +
a
e’ l’area della regione compresa tra la curva in questo intervallo ed il segmento (a, b)
sull’asse delle ascisse (vedi Figura 1.10).
10
8
6
4
2
0.0
0.5
1.0
1.5
2.0
2.5
3.0
a
b
Figura 1.10: L’integrale della funzione f (x), riportata nel grafico, tra a e b e’ l’area
della parte tratteggiata.
10
8
6
4
2
0.0
0.5
1.0
1.5
2.0
2.5
3.0
a
b
Figura 1.11: L’integrale della funzione f (x), secondo Riemann.
In termini piu’ concreti l’integrale (secondo Riemann) e’ definito dal processo di limite
illustrato in Figura 1.11. Si divide l’area di interesse in tanti rettangoli di ampiezza
∆xi = xi+1 − xi ,
x1 = a,
19
xn+1 = b
(1.97)
e si approssima l’area con la somma delle aree dei rettangoli e poi si prende il limite per
∆xi → 0. In formule
Z b
n
X
f (xi )∆xi
(1.98)
f (x)dx = lim
∆xi →0
a
i=1
Consideriamo adesso una primitiva di f (x). Dunque una funzione tale che
dF (x)
= f (x)
dx
(1.99)
Dunque possiamo scrivere in via approssimata
F (xi+1 ) ≈ F (xi ) + (xi+1 − xi )f (xi )
(1.100)
∆xi f (xi ) ≈ F (xi+1 ) − F (xi )
(1.101)
od anche
da cui
Z
b
f (x)dx = lim
∆xi →0
a
n
X
(F (xi+1 − F (xi ))
(1.102)
i=1
Scriviamo i vari termini di questa somma nel seguente modo
F (x2 ) − F (x1 ) +
+ F (x3 ) − F (x2 ) +
+ F (x4 ) − F (x3 ) +
+ ··· +
+ F (xn ) − F (xn−1 ) +
+ F (xn+1 ) − F (xn )
(1.103)
Chiaramente i termini di questa somma si annullano a due a due ed il risultato e’ semplicamente F (b) − F (a). Dunque abbiamo dimostrato il teorema fondamentale del calcolo
integrale che dice l’integrale definito e quello indefinito sono connessi dalla seguente
relazione
Z
b
a
f (x)dx = F (b) − F (a)
(1.104)
dove F (x) e’ la primitiva di f (x). La costante arbitraria che appare nel calcolo dell’integrale indefinito di f (x) (o della primitiva) non ha effetto nel calcolo dell’integrale definito,
dato che nella differenza F (b) − F (a) si cancella. Facciamo un semplice esempio
Z
2
1
x2 dx =
7
x3 8 1
x3 − = − =
3 x=2
3 x=1 3 3
3
20
(1.105)
1.6
Numeri complessi
I numeri complessi nascono dall’esigenza di trovare comunque delle soluzioni alle equazioni algebriche di secondo grado che, com’e’ noto, nel caso di discriminante negativo non
ammettono soluzioni reali. L’esempio piu’ semplice e’ quello dell’equazione
x2 = −1
(1.106)
Il modo in cui viene risolto il problema e’ quello di definire un numero nuovo, non reale,
che e’ indicato con la lettera i (immaginario in contrasto ai numeri reali), tale che
i2 = −1
(1.107)
Questo permette di allargare il campo dei numeri reali introducendo delle nuove quantita’
(i numeri complessi) che sono determinati da una coppia di reali:
z = a + ib
(1.108)
Im z
z
b
a
Re z
Figura 1.12: La rappresentazione di un numero complesso come un punto sul piano.
I numeri reali a e b si dicono rispettivamente parte reale (Re z) e parte immaginaria
(Im z) di z. Notiamo che un numero complesso con parte immaginaria nulla e’ un numero reale. Possiamo introdurre la moltiplicazione tra due numeri complessi, in modo da
rispettare le consuete regole algebriche aumentate della regola i2 = −1. Si ha dunque
z1 z2 = (a1 + ib1 )(a2 + ib2 ) = a1 a2 − b1 b2 + i(b1 a2 + a1 b2 )
(1.109)
Se sia z1 che z2 hanno parte immaginaria nulla (b1 = b2 = 0), la regola precedente si riduce
al prodotto a1 a2 . Si ritrova cosi il prodotto di due numeri reali. In particolare il prodotto
21
di un numero reale per un numero complesso (nel caso precedente b1 = 0) da’
a1 z2 = a1 a2 + ia1 b2
(1.110)
Si definisce il complesso coniugato di un numero complesso tramite l’operazione di trasformare i → −i. Precisamente
z ∗ = (a + ib)∗ = a − ib
(1.111)
Il modulo quadro di z e’ una quantita’ positiva ed e’ data da
|z|2 = zz ∗ = (a + ib)(a − ib) = a2 + b2 ≥ 0
(1.112)
Dato che un numero complesso e’ identificato da una coppia di numeri reali, lo possiamo
anche descrivere in termini di punti su un piano, in cui l’asse x e l’asse y siano rappresentati
dalla parte reale e dalla parte immaginaria del numero complesso (vedi Figura 1.12). Possiamo dare anche un’altra rappresentazione di z usando coordinate polari. Cioe’ possiamo
scrivere
a = ρ cos θ, b = ρ sin θ
(1.113)
da cui
z = ρ(cos θ + i sin θ)
(1.114)
Il numero ρ e’ correlato semplicemente al modulo quadro di z. Infatti usando la rappresentazione polare si ha
|z|2 = ρ2 (cos θ + i sin θ)(cos θ − i sin θ) = ρ2 (cos2 θ + sin2 θ) = ρ2
(1.115)
Dunque
ρ=
p
|z|2
(1.116)
Esiste una importantissima relazione, chiamata l’identita’ di Eulero, tra l’espressione trigonometrica di un numero complesso di modulo 1 ed il numero di Eulero, indicato con la
lettera e, data da
eiθ = cos θ + i sin θ
(1.117)
Notiamo intanto che entrambi i membri hanno modulo 1. Per il secondo membro vedi
l’equazione (1.115). Per il primo membro ricordiamo una identita’ algebrica valida per
potenze con la stessa base
ax ay = ax+y
(1.118)
Segue
da cui
eiθ1 eiθ2 = ei(θ1 +θ2 )
(1.119)
∗
|eiθ |2 = eiθ eiθ = eiθ e−iθ = 1
(1.120)
22
Siamo ora in grado di dimostrare le equazioni (1.10), assumendo l’identita’ di Eulero.
Usando su entrambi i membri della (1.119) questa identita’ si ha
ei(θ1 +θ2 ) = cos(θ1 + θ2 ) + i sin(θ1 + θ2 )
eiθ1 eiθ2
= (cos θ1 + i sin θ1 ) (cos θ2 + i sin θ2 ) =
= cos θ1 cos θ2 − sin θ1 sin θ2 + i(sin θ1 cos θ2 + sin θ2 cos θ1 )
(1.121)
(1.122)
Dato che due numeri complessi sono uguali se e solo se hanno uguale parte reale e parte
immaginaria, confrontando queste due espressioni vediamo che le relazioni che si ottengono
sono esattamente le (1.10).
Dimostriamo adesso l’identita’ di Eulero. Consideriamo le due funzioni
f1 (θ) = eiθ ,
Si ha
f2 (θ) = cos θ + i sin θ
(1.123)
df1 (θ)
= if1 (θ)
dθ
(1.124)
df2 (θ)
= − sin θ + i cos θ = i(cos θ + i sin θ) = if2 (θ)
dθ
(1.125)
Inoltre
f1 (0) = 1,
f2 (0) = 1
(1.126)
Dunque f1 (θ) e f2 (θ) coincidono ovunque, dato che soddisfano la stessa equazione differenziale del primo ordine e coincidono in θ = 0. Dalla formula di Eulero segue quella che
viene considerata la piu’ bella formula della matematica perche’ connette il numero
e, π, l’unita’ immaginaria e −1. Infatti se nella formula di Eulero scegliamo θ = π segue
subito
eiπ = −1
(1.127)
1.7
Le matrici
Una matrice e’ una collezione di n × m numeri (in genere considereremo numeri complessi)
che indicheremo con il simbolo
mij ,
i = 1, · · · , n,
j = 1, · · · , m
(1.128)
In genere questi numeri si dispongono in un rettangolo che si denota complessivamente
con un unico simbolo, per esempio, M


m11 m12 · · · m1m
 m21 m22 · · · m2m 


(1.129)
M = .
.. 
..
..
 ..
. 
.
.
mn1 m2n · · · mnm
23
I singoli numeri mij sono detti elementi della matrice M . Il primo indice determina la
riga, mentre il secondo indice la colonna. Facciamo alcuni esempi:
0 1
Matrice 2 × 2 :
(1.130)
1 0
0
Matrice 2 × 1 :
(1.131)
1
Matrice 1 × 2 :
1 0
(1.132)
Le matrici come le ultime due sono anche dette vettori. Nel primo caso si parla di un
vettore colonna, nel secondo caso di un vettore riga. Le matrici di ordine n × m formano
uno spazio vettoriale di dimensione n × m, con la somma di due matrici definita da:
(A + B)ij = Aij + Bij
(1.133)
(αA)ij = αAij
(1.134)
ed il prodotto
Per matrici 2 × 2 questo significa
′ ′ a b
a + a′ b + b′
a b
=
+
c + c′ d + d′
c′ d′
c d
e
α
a b
c d
=
αa αb
αc αd
(1.135)
(1.136)
E’ possibile definire un prodotto tra due matrici A e B se il numero di colonne di A e’
uguale al numero di righe di B. Precisamente se A e’ di ordine m1 × n e B n × m2 , allora
il loro prodotto, una matrice m1 × m2 , e’ dato da
Cij =
n
X
Aik Bkj
(1.137)
k=1
Piu’ esplicitamente si ha
C11
C12
···
C1m2
C21
···
Cij
···
Cm1 m2
= A11 B11 + A12 B21 + · · · + A1n Bn1
= A11 B12 + A12 B22 + · · · + A1n Bn2
= A11 B1m2 + A12 B2m2 + · · · + A1n Bnm2
= A21 B11 + A22 B21 + · · · + A2n Bn1
= Ai1 B1j + Ai2 B2j = · · · + Ain Bnj
= Am1 1 B1m2 + Am1 2 B2m2 + · · · + Am1 n Bnm2
(1.138)
Il prodotto cosi’ definito si chiama prodotto righe per colonne. Infatti, se guardiamo
l’espressione precedente, vediamo che, per esempio, l’elemento C11 , e’ dato dalla somma
24
dei prodotti dei termini della prima riga di A per i corrispondenti della prima colonna di
B. Nello stesso modo, l’elemento Cij e’ dato dalla somma dei prodotti dei termini della
riga i-ma di A per i corrispondenti della colonna j-ma di B. Diamo alcuni esempi di
prodotti. Il prodotto di due matrici 2 × 2 e’ ancora una matrice 2 × 23
0 1
1 0
0 −1
=
(1.139)
1 0
0 −1
1 0
Il prodotto di una matrice 2 × 2 per una 2 × 1 (un vettore) e’ ancora un vettore 2 × 14
0 1
0
1
=
(1.140)
1 0
1
0
Analogamente il prodotto di un vettore 1 × 2 per una matrice 2 × 2 e’ un vettore 1 × 25
0 1
0 1
= 1 0
(1.141)
1 0
Notiamo infine che il prodotto di un vettore 1 × n per un vettore n × 1 da’ una matrice
1 × 1 cioe’ un numero. Per esempio
a′
a b
= aa′ + bb′
(1.142)
b′
Nel caso di matrici quadrate si definisce una quantita’ importante che e’ il determinante. Importante, in particolare, perche’ un sistema di n equazioni lineari in n incognite
si riconduce ad un calcolo di determinanti di matrici costruite con i coefficienti delle equazioni del sistema. In particolare, se si ha un sistema lineare omogeneo, cioe’ senza termini
noti, quale per esempio
a11 x + a12 y = 0,
a21 x + a22 y = 0
(1.143)
si puo’ dimostrare che si hanno soluzioni non nulle se e solo se il determinante della matrice
dei coefficienti e’ nullo. In questo caso il determinante e’ dato da
a11 a12
= a11 a22 − a21 a12
(1.144)
Det
a21 a22
In generale il determinante si ottiene prendendo tutti i possibili prodotti di elementi che
non appartengono alla stessa riga e alla stessa colonna e combinandoli assieme con un
opportuno segno in fronte a ciascuno di essi. Senza entrare in dettagli diciamo che esiste
3
In genere il prodotto di due matrici quadrate n × n e’ ancora una matrice quadrata dello stesso
ordine
4
In generale il prodotto di una matrice n × n per il vettore n-dimensionale, n × 1, e’ ancora un
vettore n-dimensionale
5
Anche qui in generale, un vettore 1 × n per una matrice quadrata n × n da’ un vettore di tipo
1×n
25
un metodo ricorsivo per calcolare i determinanti
righe (o per colonne). Consideriamo ad esempio il


a11 a12 a13
Det  a21 a22 a23  =
a31 a32 a33
a21
a22 a23
− a12 Det
= a11 Det
a31
a32 a33
effettuando il cosi detto sviluppo per
determinante di una matrice 3 × 3
a23
a33
+ a13 Det
a21 a22
a31 a32
(1.145)
Come si vede il segno di ogni termine e’ scelto positivo o negativo se la somma degli indici
del coefficiente dell’elemento per il quale si sta sviluppando e’ pari o dispari rispettivamente. Inoltre le sottomatrici sono ottenute cancellando dalla matrice iniziale l’intera
riga e l’intera colonna corrispondenti all’elemento dello sviluppo. Il metodo si applica a
qualunque riga o colonna da cui sia preferibile partire. Ovviamente e’ conveniente partire
dalla riga o dalla colonna che ha piu’ elementi nulli perche’ questo diminuisce il numero di
sotto-determinanti da calcolare. Da queste regole si vede facilmente che il determinante e’
una somma di termini costituita da tutti i possibili prodotti di elementi di matrice che non
appartengono alla stessa riga e alla stessa colonna, presi ognuno con un segno opportuno.
Per esempio tra i vari prodotti appare il prodotto di tutti gli elementi della diagonale
principale (quella che va da sinistra a destra) preso con il segno positivo. Questi termini
si chiamano anche prodotti dedotti.
Per matrici quadrate a determinante non nullo e’ possibile trovare una matrice inversa,
definita dalla regola
AA−1 = A−1 A = I
(1.146)
dove I e’ la matrice identita’, cioe’ una matrice con tutti 1 sulla diagonale principale e
zero in tutti gli altri posti). In componenti
n
X
Aji (A−1 )ik =
n
X
(A−1 )ji Aik = δjk
(1.147)
i=1
i=1
Il simbolo δjk e’ detto la δ di Kronecker ed e’ uguale ad 1 per j = k e zero in tutti gli altri
casi. Per esempio, se si ha la matrice 2 × 2
a11 a12
(1.148)
A=
a21 a22
allora l’inversa e’ data da
A−1 =
1
DetA
a22 −a12
−a21 a11
26
(1.149)
Capitolo 2
Cenni di fisica
2.1
Introduzione
Una delle questioni piu’ interessanti relative alla concezione del mondo che ci circonda e’
sempre stata la seguente: la materia, allo stato piu’ elementare, ha composizione corpuscolare o piuttosto continua? Questa domanda deriva a sua volta dal problema di cosa
succeda qualora si continui a dividere un pezzo di materia. E’ possibile continuare questo
processo di divisione sino all’infinito? In questo caso potremo parlare di continuita’ della
materia. Se invece il processo di divisibilita’ ha termine perche’ alla fine non ci e’ possibile effettuare ulteriori divisioni, parleremo di costituzione corpuscolare della materia.
Nel periodo che va dal 600 al 300 AC molti pensatori greci (Talete, Anassimene, Eraclito, Empedocle, Platone e Aristotele) formularono o sostennero l’idea che la materia fosse
costituita da quattro elementi, aria, acqua, terra e fuoco che producevano varie sostanze
tramite processi di rarefazione e di condensazione. Questo portava all’idea di una continuita’ della materia elementare. La posizione opposta fu assunta da Democrito (verso il
460 AC), che introdusse l’idea di atomi1 . Questi atomi erano uguali, eccetto per la forma,
la grandezza ed il moto. Quindi i vari elementi derivavano da una diversa disposizione
degli atomi stessi. Uno dei problemi della concezione di Democrito e’ che questa portava
necessariamente all’idea di vuoto. Infatti tra un atomo e l’altro non esiste materia. Leucippo (≈ 450 AC), Epicuro (347-271 AC) e Lucrezio (98-55 AC) appoggiarono le idee di
Democrito, ma in genere questa idea fu abbandonata per il sopravvento delle idee di Platone e Aristotele che aborrivano l’idea del vuoto e che quindi preferivano l’idea dei quattro
elementi. Questa idea permase per molti secoli. Finalmente Cartesio (1596-1650) riprese
l’idea corpuscolare, sebbene anche lui fosse contrario al vuoto. L’affermazione definitiva
dell’idea corpuscolare, o meglio dell’idea atomica, avvenne grazie alle ricerche fatte sui gas
ed allo sviluppo della chimica. Di particolare rilievo fu il contributo di Dalton (1766-1844)
che introdusse l’idea che tutti gli atomi che costituiscono lo stesso elemento2 fossero identici tra loro. Nonostante che le evidenze della chimica fossero di natura schiacciante, fino
1
2
Dal greco ατ øµøς che significa indivisibile
L’idea che gli elementi costituiscano tutte le sostanze fu introdotta da Boyle (1627-1691)
27
ai primi del novecento c’erano ancora molti scienziati che mettevano in dubbio l’effettiva
realta’ degli atomi. Per esempio lo stesso Einstein nella sua tesi di abilitazione del 1905
affrontava i metodi di misura delle dimensioni molecolari, lavoro teso a rafforzare le idee
corpuscolari sulla materia. Nello stesso anno dava anche un contributo decisivo alle idee
atomiche con il suo lavoro sul moto browniano.
Tutta la discussione precedente si riferisce in realta’ ad una descrizione puramente
cinematica della materia. Dal punto di vista dinamico, dopo la formulazione delle leggi di
Newton (1643-1727) si era consolidata l’idea di una rappresentazione completamente meccanicistica dell’universo, l’idea cioe’ di un universo riconducibile ad un modello puramente
meccanico descritto appunto dalle leggi di Newton. In particolare si tento’ di descrivere
anche i fenomeni luminosi in termini meccanici. Newton stesso formulo’ una teoria corpuscolare della luce. Questa era anche giustificata da quella parte dell’ottica, nota come
ottica geometrica, che descrive la luce come composta da raggi che attraversano lo spazio
in modo rettilineo essendo poi riflessi od assorbiti dalle superfici incontrate. Questo poteva essere chiaramente interpretato in termini di moti di particelle. Quest’ idea si scontro’
successivamente con la scoperta di vari fenomeni, quali la diffrazione e l’interferenza che
non potevano essere spiegati nei termini corpuscolari, ma piuttosto in termini di onde3 .
In realta’ l’idea di moti ondosi si era gia’ largamente diffusa nei domini dell’acustica e
della dinamica dei fluidi. Infatti, anche se l’aria e l’acqua sono composti da atomi ed hanno
quindi struttura corpuscolare, se consideriamo fenomeni che avvengono su una scala D,
molto grande rispetto alle dimensioni interatomiche d4 , il mezzo (aria o acqua) puo’ di fatto
essere considerato come un continuo. I fenomeni interessanti che avvengono in un mezzo
continuo sono fenomeni di disturbo del mezzo stesso e vengono schematizzati nel seguente
modo. Noi siamo interessati a cosa avviene nei vari punti del mezzo. Indichiamo il generico
punto con P . Per esempio nel caso di un bacino d’acqua possiamo iniziare considerando
tutta l’acqua ferma. Questa situazione viene descritta come lo stato di equilibrio o stato
fondamentale del sistema. Possiamo poi considerare un disturbo (dovuto ad una qualunque
ragione), per cui, invece di avere lo specchio d’acqua immobile, in ogni punto P , il livello
dell’acqua varia con il tempo. Questo fenomeno si puo’ allora descrivere in termini di
una funzione h(P, t) che descrive la variazione di altezza del liquido nel punto P ed al
tempo t rispetto al livello di equilibrio. La quantita’ h(P, t) e’ detta un campo e nel caso
specifico un campo scalare perche’ associa ad ogni punto e ad ogni istante un numero:
h(P, t). Un altro esempio di campo scalare e’ la variazione di pressione nell’aria. Anche
questa puo’ essere descritta da un campo scalare p(P, t) che ci fornisce la variazione di
pressione ripetto alla pressione in aria quieta in ogni punto P e ad ogni istante t. Un
altro esempio di campo scalare e’ la temperatura nei vari punti di una stanza ad un dato
istante di tempo T (P, t). In altri casi puo’ avere interesse avere informazioni che non si
riducono ad un puro numero. Per esempio potremmo essere interessati a conoscere ad
3
A questo contribuirono i lavori di Huygens, Fresnel e quello definitivo di Young nel 1801 con
il famoso esperimento della doppia fenditura, vedi in seguito
4
Stiamo cioe’ assumendo d ≪ D
28
ogni istante la velocita’ dell’acqua nei vari punti di una condotta. La velocita’ e’ una
~ (P, t),
grandezza vettoriale e quindi l’informazione puo’ essere codificata in tre campi, V
che rappresentano le tre componenti della velocita’ in un dato sistema di riferimento. In
questo caso si parla di un campo vettoriale. Da un punto di vista matematico, un campo
scalare e’ una applicazione di R3 × R → R, dove R3 rappresenta lo spazio tridimensionale,
il primo R e’ il campo reale nel quale varia il tempo, mentre il secondo R non e’ altro che
lo spazio dei valore assunti dalla funzione scalare, cioe’ nei vari casi, h(P, t), p(P, t), ecc.
Nel caso di campi vettoriali si ha una applicazione da R3 × R → R3 .
Come abbiamo detto, questi campi rappresentano in genere la variazione dello stato
del mezzo rispetto ad una situazione di equilibrio. Nel caso dell’altezza dell’acqua h, e’
la variazione dell’altezza rispetto al caso di acqua stagnante. p e’ essere la variazione
~ ci fornisce
della pressione rispetto ad una situazione di pressione costante. Il campo V
la velocita’ dell’acqua rispetto allo stato in cui l’acqua e’ ferma e cosi via. Nonostante
tutti questi campi rappresentino delle situazioni fisiche molto diverse, quando le variazioni
rispetto alla situazione di equilibrio sono piccole, si hanno situazioni completamente analoghe sul piano matematico. Infatti sotto queste condizioni tutti questi campi descrivono
delle propagazioni ondose. Cioe’ soddisfano un’equazione, detta equazione delle onde.
Dunque l’dea di onde era piuttosto diffusa a seguito degli studi sulla propagazione
dei disturbi nei mezzi. Quando risulto’ evidente che anche la luce dava luogo a fenomeni
di diffrazione e di interferenza, le idee corpuscolari in merito svanirono rapidamente e si
affermo’ in maniera definitiva la descrizione ondulatoria. Alla fine dell’ottocento la teoria
di Maxwell, che prevedeva che la radiazione elettromagnetica soddisfacesse un’equazione
d’onda, fu l’affermazione definitiva della teoria ondulatoria della luce, anche per la maniera
unitaria in cui i fenomeni elettrici e magnetici venivano trattati.
Dunque alla fine dell’ottocento si era in una situazione in cui la materia veniva descritta in maniera corpuscolare, mentre la radiazione elettromagnetica in termini di onde.
Ovviamente gli irriducibili sostenitori delle idee newtoniane cercarono di interpretare le
equazioni di Maxwell in termini meccanicistici. La questione stava in una possibile interpretazione delle onde em come spostamenti di particelle che costituiscono il mezzo in cui
si propagano, cosi come le onde acustiche o le onde di velocita’. In questi casi l’onda esiste
perche’ c’e’ un mezzo materiale che la supporta. Ma quale e’ questo mezzo nel caso della
luce? Si introdusse allora l’idea di etere come il mezzo che, per cosi’ dire, riempie il vuoto
e le cui vibrazioni originano i campi elettromagnetici. Questa idea fu spazzata in modo
definitivo dalla teoria di Einstein (ci riferiamo alla teoria della relativita’ ristretta). Da
quel momento in poi il campo elettromagnetico fu pensato semplicemente in termini di
campi elettrici e magnetici che si propagano nel vuoto. Cioe gli oggetti che vibrano sono
i campi elettromagnetici.
Piu’ o meno nello stesso periodo cominciarono ad emergere fatti nuovi che mettevano in crisi i due pilastri della fisica classica, l’equazione di Newton e quelle di Maxwell.
Descriveremo poi questi fenomeni. In questa introduzione e’ sufficiente dire che il primo
colpo fu assestato alla teoria ondulatoria della luce con l’analisi di Planck del corpo nero
(1900) e l’idea successiva di Einstein che la luce fosse costituita da corpuscoli (fotoni) con
29
energia quantizzata. Questa ipotesi permetteva di spiegare l’effetto Compton (1922), che
consiste nel cambiamento di frequenza della luce quando e’ diffusa da un elettrone. Lo
studio dei sistemi atomici portava a concludere che la fisica classica non era in grado di
spiegare la stabilita’ degli atomi che, al contrario, sarebbero dovuti collassare in tempi
brevissimi. L’analisi di Bohr (1913) mostrava che le leggi che regolano i sistemi microscopici dovevano subire una revisione profonda. Nel 1923 De Broglie formulava l’ipotesi che
cosi come la luce mostra un duplice aspetto, ondulatorio e corpuscolare, anche la materia
doveva possedere un duplice aspetto, corpuscolare e ondulatorio. Nel 1927 Davisson e
Germer mostrarono che gli elettroni possono dare luogo ad un fenomeno di interferenza,
mettendone cosi in luce l’aspetto ondulatorio. In questo periodo gli sviluppi procedettero
a velocita’ straordinaria. Nel gennaio del 1925 Pauli enunciava il principio di esclusione e
nel luglio dello stesso anno Heisenberg, con la collaborazione di Born e Jordan, formulava
la meccanica delle matrici che permetteva di effettuare veri e propri calcoli quantistici,
tant’e’ vero che Pauli nel Gennaio del 1926 fu capace di usare le meccanica di Heisenberg
per calcolare l’energia dei livelli dell’atomo di idrogeno. Dopo una decina di giorni usci’ il
primo di una serie di articoli di Schrödinger sulla formulazione ondulatoria della meccanica
quantistica. Questa teoria fu poi mostrata essere equivalente a quella di Heisenberg ma
offriva il fondamentale vantaggio, per i fisici dell’epoca, di essere espressa in termini di
equazioni differenziali, invece che in termini di matrici, tecnica quest’ultima scarsamente
nota ai fisici di allora. Nel febbraio dello stesso anno Fermi, durante la sua permanenza
di due anni presso l’Istituto di Fisica dell’Universita’ di Firenze scrisse il primo lavoro
su quella che poi sarebbe stata conosciuta come la statistica di Fermi-Dirac. Ancora
nel mese di Giugno Born scrisse il primo lavoro sulla interpretazione probabilistica della
meccanica quantistica. Con questo lavoro si puo’ dire che la meccanica quantistica fosse
completamente formulata nella versione nota come l’interpretazione di Copenhagen.
Come abbiamo visto nell’introduzione i capisaldi della fisica classica alla fine
dell’ottocento erano la teoria di Newton e le equazioni di Maxwell. Qui daremo una
breve introduzione su come la teoria di Newton possa essere riformulata in maniera
da poter consentire un confronto diretto con quelli che saranno i postulati della
meccanica quantistica. Per quanto concerne invece le equazioni di Maxwell, sarebbe
troppo lungo e complicato discuterne. Ci limiteremo dunque ad esporre alcune delle
proprieta’ delle onde.
2.2
I postulati della meccanica classica
Consideriamo il caso semplice di un moto unidimensionale di una particella puntiforme di massa m soggetta ad una forza F (x). L’equazione di Newton che descrive
il moto della particella risulta essere5
m
d2 x(t)
≡ mẍ(t) = F (x(t))
dt2
5
(2.1)
E’ uso indicare le derivate prime e seconde rispetto al tempo con uno o due punti
rispettivamente.
30
Questa equazione determina completamente il moto della particella nel senso che se
si assegnano i valori al tempo t = 0 della posizione x(0) e della velocita’ dx(t)/dt|t=0 ≡
ẋ(0), il moto ai tempi successivi e’ completamente determinato, cioe’ dall’equazione precedente possiamo calcolare x(t). Questo problema si puo’ riformulare
introducendo la variabile di impulso che e’ semplicemente connessa alla velocita’:
p(t) = mẋ(t)
(2.2)
In questi termini la singola equazione del moto, del secondo ordine nelle derivate
temporali, viene convertita in due equazioni differenziali del primo ordine
ẋ(t) =
p
,
m
ṗ(t) = F (x(t))
(2.3)
Se esiste una funzione V (x) (che nel caso unidimensionale esiste sempre ma non e’
detto che esista in generale), tale che
F (x) = −
allora
p(t)
ẋ(t) =
,
m
dV (x)
dx
(2.4)
dV (x) ṗ(t) = −
dx x=x(t)
(2.5)
In questo caso si puo’ introdurre una funzione delle variabili p e x (detta l’hamiltoniana del sistema) data da
p2
+ V (x)
(2.6)
H=
2m
in termini della quale le due equazioni del moto (2.5) si possono scrivere nella forma
ẋ(t) =
∂H
,
∂p
ṗ(t) = −
∂H
∂x
(2.7)
Un sistema di equazioni cosi fatto si chiama sistema hamiltoniano e le due variabili (x, p) vengono dette canonicamente coniugate. Si dice anche che p e’
coniugata a x e viceversa, o che x e p sono una coppia di variabili coniugate. Nel
caso in esame la funzione H ha anche il significato di energia meccanica del sistema, essendo la somma dell’energia cinetica p2 /2m = mẋ2 /2 e dell’energia potenziale
V (x). Ma indipendentemente dal significato fisico particolare di x e p un sistema
di equazioni cosi’ fatto e’ estremamente generale ed e’ in grado di descrivere molti
tipi di sistemi fisici. Notiamo anche che se introduciamo il piano (x, p), le condizioni
iniziali x(0) e p(0) sono rappresentate da un punto e la soluzione delle equazioni
del moto (x(t), p(t) da’ luogo ad una linea passante da (x(0), p(0)), come si vede in
Figura 2.1. Lo spazio (in questo caso il piano) descritto dalle variabili (x, p) viene
detto lo spazio delle fasi e quindi il moto di una particella si puo’ pensare come al
moto di un punto in questo spazio le cui coordinate ci danno, istante per istante,
31
p
(x(0), p(0))
x
Figura 2.1: Viene mostrata la traiettoria della particella nel piano (x, p) che al tempo
t = 0 passa dal punto di coordinate (x(0), p(0))
la posizione e l’impulso (o la velocita’ v = p/m) della particella. Consideriamo un
semplice esempio
p2
− kx
(2.8)
H=
2m
segue
p
ẋ = , ṗ = k
(2.9)
m
Assumendo (x(0), p(0)) = (0, 0) si ha dalla seconda
p(t) = kt
(2.10)
k
t
m
(2.11)
k 2
t
2m
(2.12)
e sostituendo nella prima
ẋ(t) =
da cui
x(t) =
eliminando t
t=
si ha infine
x(t) =
p(t)
k
1 2
p (t)
2mk
32
(2.13)
(2.14)
p
x
Figura 2.2: La soluzione delle equazioni (2.9).
o
p(t) =
p
2mkx(t)
(2.15)
Questa equazione descrive la curva di Figura 2.2, che rappresenta una particella che
si muove di moto accelerato con accelerazione k/m. Risulta che la maggior parte dei
sistemi fisici di interesse sono descrivibili in termini di un sistema hamiltoniano, cioe’
da n variabili di tipo x che vengono indicate tradizionalmente con qi , i = 1, · · · n
e da n variabili di tipo p, che denoteremo con pi . Dunque, per ipotesi, esiste una
hamiltoniana H(qi , pi ) che dà luogo alle 2n equazioni di Hamilton
q̇i =
∂H(qi , pi )
,
∂pi
ṗi = −
∂H(qi , pi)
∂qi
(2.16)
Assegnando i 2n valori iniziali (qi (0), pi (0)) queste equazioni descrivono una unica
curva nello spazio delle fasi 2n-dimensionale delle variabili (qi , pi ). Quindi per ogni
punto dello spazio delle fasi passa una ed una sola soluzione delle equazioni di Hamilton. Il sistema delle equazioni di Hamilton è dunque completamente deterministico,
perche’ assegnate le condizioni iniziali è possibile prevedere cosa succederà ad ogni
istante futuro (o cosa e’ successo ad ogni istante passato).
Il concetto di sistema hamiltoniano è estremamente più generale di come possa
apparire da questi cenni introduttivi. Anche sistemi apparentemente scorrelati dalla
dinamica del punto, quali per esempio i moti delle onde, si possono riportare ad un
sistema hamiltoniano, sebbene con un continuo di gradi di libertà invece che con un
numero discreto come qui considerato.
Siamo ora in grado di enunciare i postulati della meccanica classica:
33
1. Lo stato di un sistema è caratterizzato ad ogni istante dalle 2n variabili (qi , pi),
cioè da un punto nello spazio delle fasi.
2. Ogni variabile dinamica ω è funzione delle coordinate (qi , pi ), ω ≡ ω(qi , pi).
Per esempio, l’hamiltoniana è una loro funzione.
3. Se il sistema si trova nello stato caratterizzato da (qi , pi ), la misura di ω dà con
certezza il valore ω(qi , pi). E’ sempre possibile fare una misura ideale, cioe’
una misura per cui lo stato del sistema rimane inalterato dopo la misura, cioè
la posizione nello spazio delle fasi non cambia. Questo significa che il processo
di misura non interferisce con il sistema (come vedremo questo postulato viene
abbandonato in meccanica quantistica).
4. Lo stato del sistema si evolve nel tempo in accordo alle equazioni di Hamilton
q̇i =
∂H(qi , pi )
,
∂pi
ṗi = −
∂H(qi , pi )
∂qi
(2.17)
Il generico sistema classico e’ dunque caratterizzato dai suoi gradi di liberta’ e
dalla sua hamiltoniana. Con questi elementi ed i postulati assegnati si puo’ determinare completamente il moto del sistema (assegnando il punto nello spazio delle fasi
all’istante iniziale). Per esempio, la descrizione del moto di un punto, nella meccanica di Newton ed in quella relativistica di Einstein, differisce solo per la forma di
H, ma valgono sempre i postulati precedenti.
Nella meccanica analitica giocano un ruolo primario le parentesi di Poisson
che, come vedremo, hanno un importante analogo quantistico. Le parentesi di Poisson intervengono allorche’ si sia interessati a calcolare la variazione temporale di una
generica variabile dinamica ω(qi (t), pi(t), t), calcolata lungo la traiettoria del sistema
nello spazio delle fasi. Si ha
n dω
∂ω X ∂ω
∂ω
=
+
q̇i +
ṗi
(2.18)
dt
∂t
∂q
∂p
i
i
i=1
ed usando le equazioni di Hamilton (2.17)
n dω
∂ω X ∂ω ∂H
∂ω ∂H
=
+
−
dt
∂t
∂qi ∂pi
∂pi ∂qi
i=1
(2.19)
Date due variabili dinamiche A e B, la loro parentesi di Poisson è definita da
n X
∂A ∂B ∂A ∂B
{A, B} =
−
(2.20)
∂qi ∂pi ∂pi ∂qi
i=1
Dunque
∂ω
dω
=
+ {ω, H}
dt
∂t
34
(2.21)
Le parentesi di Poisson godono di alcune importanti proprietà algebriche che possono
essere verificate immediatamente:
{A, B} = −{B, A}
(2.22)
{A, B + C} = {A, B} + {A, C}
(2.23)
{A, BC} = {A, B}C + B{A, C}
(2.24)
Inoltre, essendo qi e pi variabili indipendenti si ha
{qi , qj } = {pi , pj } = 0,
2.3
{qi , pj } = δij
(2.25)
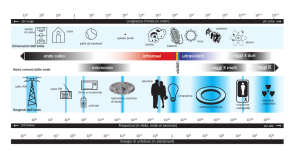
Onde
Un’onda e’ una perturbazione che si propaga attraverso lo spazio trasportando energia ma non materia. Ad eccezione della radiazione elettromagnetica, ed a livello
teorico della radiazione gravitazionale, che possono propagarsi nel vuoto, gli altri
tipi di onde si propagano in un mezzo che, per deformazione, e’ in grado di produrre
forze elastiche di ritorno. Attraverso il mezzo, le onde possono viaggiare e trasferire
energia da un punto all’altro, senza che alcuna particella del mezzo venga dislocata permanentemente. Ogni punto, od ogni particella materiale, interagisce con le
particelle vicine ed e’ quindi in grado di trasferire energia. Non esiste, quindi, un
trasporto di massa associato, ogni punto oscilla attorno a una posizione fissa. Intuitivamente il concetto di onda e’ associato al trasporto di una perturbazione nello
spazio, ma non e’ associato con il moto del mezzo che occupa lo spazio stesso. In
un’onda, l’energia vibrazionale si muove dalla sorgente sotto forma di perturbazione
senza un moto collettivo del mezzo in cui si propaga.
La teoria delle onde rappresenta una particolare branca della fisica teorica che
riguarda lo studio delle onde indipendentemente dalla loro origine fisica. Questa
peculiarita’ deriva dal fatto che la teoria matematica delle onde puo’ essere usata
per descrivere fenomeni ondulatori in contesti anche molto differenti. Per esempio
l’acustica si distingue dall’ottica per il fatto che la prima si occupa del trasporto
vibrazionale di energia meccanica, mentre la seconda di perturbazioni del campo
elettrico e magnetico. Concetti come massa, inerzia, quantita’ di moto, elasticita’
diventano quindi cruciali per descrivere i processi ondulatori acustici, al contrario
dell’ottica. La struttura particolare del mezzo introduce inoltre alcuni fattori di cui
bisogna tenere conto, come ad esempio i fenomeni vorticosi per l’aria e l’acqua o la
complessa struttura cristallina nel caso di alcuni solidi. Per esempio, basandosi sull’origine meccanica delle onde acustiche, ci puo’ essere un movimento nello spazio e
nel tempo di una perturbazione se e solo se il mezzo non e’ ne’ infinitamente flessibile
ne’ infinitamente rigido. Se tutte le parti che compongono il mezzo si dispongono
in modo rigido l’una rispetto all’altra, non sara’ possibile alcun movimento relativo infinitesimo e quindi non ci sara’ alcuna onda (ad esempio l’ idealizzazione del
35
corpo rigido). Al contrario, se tutte le parti sono indipendenti l’una dall’altra senza
alcun tipo di interazione reciproca, non vi sara’ alcuna onda in quanto non ci sara’
trasmissione di energia fra le varie parti componenti del corpo.
Altre proprieta’ tuttavia possono essere usate per descrivere indifferentemente
tutti i tipi di onde. Per esempio, le onde periodiche presentano una cresta (punto
piu’ alto) ed un ventre (punto piu’ basso). Si possono poi distinguere onde longitudinali e trasversali. Nelle onde trasversali la vibrazione e’ perpendicolare alla
direzione di propagazione (ad esempio le onde di una corda vibrante, in cui le parti
infinitesime che costituiscono la corda stessa si muovono verso l’ alto e verso il basso
in verticale, mentre l’onda si propaga orizzontalmente). Le onde longitudinali sono
invece caratterizzate da una vibrazione concorde con la direzione di propagazione
dell’onda (ad esempio le onde sonore, le particelle dell’aria si muovono nella stessa
direzione di propagazione del suono). Esistono tuttavia onde che sono sia longitudinali che trasversali e sono dette onde miste (ad esempio le onde sulla superficie del
mare).
Tutte le onde hanno un comportamento comune in situazioni standard e possiedono le seguenti proprieta’:
• Riflessione: quando una onda cambia direzione incidendo su un materiale
riflettente.
• Rifrazione: il cambio di direzione di un’onda causata dal passaggio tra due
mezzi (ad esempio con densita’ diversa).
• Diffrazione: la diffusione delle onde, per esempio quando passano per una
fessura stretta (piu’ correttamente piccola rispetto alla lunghezza d’onda)
• Interferenza: la somma vettoriale (possono annullarsi) di due onde che entrano
in contatto
• Dispersione: la divisione di un’onda in sotto onde in dipendenza della loro
frequenza.
Un’onda e’ polarizzata se puo’ oscillare solo in una direzione. La polarizzazione di
un’onda trasversale descrive la direzione di oscillazione, nel piano perpendicolare alla
direzione di moto. Onde longitudinali come quelle sonore non hanno polarizzazione,
in quanto per queste onde la direzione di oscillazione e’ lungo la direzione di moto.
Un’onda puo’ essere polarizzata con un filtro polarizzatore. Nel caso dell’ottica
questo filtro puo’ essere una lente Polaroid.
A seconda del mezzo in cui si propagano e della caratteristica fisica che usiamo
per rappresentarle si hanno:
• onde elastiche o di spostamento, in cui poniamo l’attenzione sullo spostamento
delle particelle;
• onda di velocita’, se poniamo l’attenzione sulla velocita’ delle particelle;
36
• onda di densita’, se studiamo la densita’ volumica e per questo ne e’ associata
un’ onda di pressione.
• radiazione elettromagnetica che riguarda un insieme di onde come luce, onde
radio, raggi X nel cui caso la propagazione non ha bisogno di un mezzo, le
onde posso propagarsi ne vuoto;
2.3.1
Descrizione delle onde
Come abbiamo detto, le onde sono caratterizzate da funzioni delle coordinate spaziali e del tempo. Sappiamo inoltre dal teorema di Fourier (vedi dopo) che una
funzione (periodica o no) puo’ essere decomposta in termini di componenti (funzioni) periodiche, quali seno e/o coseno. La caratteristica specifica di una funzione
periodica e’ il periodo T , definito come il tempo nel quale una funzione ritorna al
valore iniziale. In formule
f (t + T ) = f (t)
(2.26)
Il periodo e’ strettamente collegato alla frequenza ν cioe’ il numero di periodi per
unita’ di tempo; se quest’unita’ e’ il secondo allora la frequenza si misura in hertz.
Queste grandezze sono correlate nel modo seguente:
1
(2.27)
T
Ad un periodo temporale corrisponde un periodo spaziale detto lunghezza d’onda λ
che e’ legata al periodo dalla velocita’ di propagazione dell’onda
ν=
λ = vT
(2.28)
Un’onda viene spesso descritta per mezzo della sua frequenza angolare (ω, radianti/secondo); quest’ultima e’ correlata alla frequenza ν secondo la formula:
ω=
2π
= 2πν.
T
(2.29)
Non tutte le onde sono sinusoidali (ovvero hanno la forma della funzione seno
e/o coseno). Come abbiamo detto, in generale si possono esprimere come somma di
sinusoidi, ma questa somma non e’ necessariamente una sinuosoide. Un esempio di
onda non sinusoidale e’ l’impulso che si muove lungo una corda poggiata per terra.
Matematicamente si ha che un’onda (teorema di Fourier) puo’ essere rappresentata
tramite la somma
X
A(x, t) =
Ak sin(kx − ωt)
(2.30)
k
con ω = kv e v la velocita’ di propagazione dell’onda. La quantita’ k si chiama
anche il vettore d’onda. Si definisce anche come lunghezza d’onda la quantita’:
k=
2π
λ
37
(2.31)
vediamo dunque che
k=
2π
ω
=
v
vT
(2.32)
e, confrontando con la precedente
λ = vT
(2.33)
Dunque la lunghezza d’onda corrisponde allo spazio di un punto che si muove con
velocita’ v in un periodo. Un’ onda sinusoidale di questo tipo e’ una soluzione
particolare dell’equazione generale delle onde ed e’ quella che di solito e’ studiata in
un primo approccio ai fenomeno ondulatori.
Notiamo che
kx − ωt = k(x − vt)
(2.34)
dunque l’argomento della funzione sinusoidale dipende solo dalla differenza x − vt.
Come vedremo tra un po’ una funzione di x − vt rappresenta un’onda che si propaga
verso destra, mentre una funzione di x + vt un’onda che si propaga in direzione
opposta. In generale si vede facilmente che generiche funzioni di x − vt o di x + vt
soddisfano l’equazione delle onde:
∂ 2 φ(x, t)
1 ∂ 2 φ(x, t)
−
=0
∂x2
v 2 ∂t2
(2.35)
La soluzione piu’ generale di questa equazione dipende da due funzioni arbitrarie
φ(x, t) = f (x − vt) + g(x + vt)
(2.36)
Per le considerazioni precedenti sin(kx±ωt) sono soluzioni particolari dell’equazione
delle onde. Il fatto che una soluzione generica la si possa esprimere come somma di
onde sinusoidali e’ conseguenza della linearita’ dell’equazione delle onde. Cioe’ se f1
e f2 sono due soluzioni, anche una generica combinazione
αf1 + βf2
(2.37)
con α e β costanti arbitrarie, e’ una soluzione.
Per capire meglio il significato di queste soluzioni consideriamo f (x − vt) e
supponiamo che la f sia una gaussiana (vedi Figura 2.3
f (y) = e−y
2 /2∆2
(2.38)
Quando y = x−vt possiamo vedere come questa curva cambia al passare del tempo.
Come si vede dai grafici in Figura 2.4, la curva si sposta con una velocita’ pari a
2, cioe’ pari al parametro v. Questo si capisce facilmente considerando il valore
f (0) = 1. Quando x − vt = 0 il valore di f e’ sempre lo stesso. Questo accade in
tutti i punti tali che x(t) = vt. Analogamente se calcoliamo, per esempio, f (0.2), in
tutti i punti per cui x(t) = vt + 0.2 la curva avra’ sempre lo setsso valore. Dunque
38
1.0
0.8
0.6
0.4
0.2
-4
2
-2
4
Figura 2.3: La curva gaussiana considerata nel testo.
f
f
f
1.0
1.0
1.0
0.8
0.8
0.8
0.6
0.6
0.6
0.4
0.4
0.4
0.2
0.2
0.2
x
-4
-2
2
4
6
8
x
-4
2
-2
4
6
8
x
-4
-2
2
4
6
Figura 2.4: La curva gaussiana, rappresentata in funzione di x, e’ fissata ai tempi
t = 0, t = 1 e t = 2 Il parametro v e’ fissato a 2.
la curva si propaga nello spazio con una velocita’ pari a v, cioe’ al parametro che
appare nella equazione delle onde.
Consideriamo una soluzione sinusoidale
ω φ(x, t) = A sin(kx − ωt) = A sin k x − t
(2.39)
k
Per quanto detto prima questa puo’ essere soluzione solo se
v=
ω
k
(2.40)
Ricordando ancora le relazioni
λ=
si ha
2π
,
k
ν=
φ(x, t) = A sin 2π
ω
2π
x
− νt
(2.41)
(2.42)
λ
Ma seno e coseno hanno un periodo di 3600, o 2π in radianti. Dunque l’espressione (2.42) e’ periodica sia nello spazio che nel tempo, con periodi dati rispettivamente
39
8
d
λ
ν
ν/ 2
2λ
Figura 2.5: Illustrazione della relazione tra frequenza e lunghezza d’onda.
da λ e T = 1/ν. Infatti
x
x+λ
φ(x + λ, t) = A sin 2π
− νt
= A sin 2π
− νt + 2π = φ(x, t)
λ
λ
(2.43)
Analogamente
x+λ
− ν(t + 1/ν)
=
φ(x, t + 1/ν) = A sin 2π
λ
x
= A sin 2π
− νt − 2π = φ(x, t)
(2.44)
λ
Abbiamo visto che vale la relazione
λ
= λν = v
T
(2.45)
dove v = c, con c la velocita’ della luce nel caso di onde elettromagnetiche. Questa
relazione puo’ essere capita anche dalla Figura 2.5 dove sono mostrati due treni
d’onde ad un tempo fissato. I due treni hanno la stessa lunghezza d, quello superiore
ha 10 creste e dato che la lunghezza d’onda non e’ altro che la distanza tra due creste
(ricordarsi la periodicita’ spaziale) , avremo per il treno d’onda superiore
d
10
(2.46)
d
= 2λ
5
(2.47)
λ=
mentre per quello inferiore
λ′ =
40
Se le onde viaggiano ad una velocita’ v, dopo un tempo t = d/v, entrambi i treni
saranno passati al di la’ dello schermo. Quindi per il treno superiore saranno passate
10 onde e 5 per quello inferiore. Pertanto le frequenze (il numero di onde per unita’
di tempo) saranno date da
ν=
10
,
t
ν′ =
5
ν
=
t
2
(2.48)
Abbiamo cosi’ mostrato che
λν = λ′ ν ′ =
2.3.2
d
=v
t
(2.49)
L’interferenza
2
2
1
1
5
-5
5
-5
-1
-1
-2
-2
2
2
1
1
5
-5
5
-5
-1
-1
-2
-2
Figura 2.6: Le quattro figure mostrano, da sinistra verso destra, la somma di due
onde sfasate rispettivamente di 00 , 450 , 900 e 1800 (nella figura gli angoli sono
espressi in radianti e corrispondono a 0, π/4, π/2 e π radianti rispettivamente).
Il fenomeno di interferenza nasce dalla maniera in cui si compongono due onde
luminose della stessa frequenza ma con fase diversa. nella Figura 2.6 si mostra la
somma di due coseni sfasati di un angolo α
cos(θ) + cos(θ + α)
(2.50)
A seconda del valore di α si ottengono risultati diversi. In particolare, quando le
onde sono in fase (prima illustrazione in alto) si ottiene un’onda che in ogni punto
ha un valore doppio, mentre quando la differenza di fase e’ 1800 (o π) si ottiene
un’onda nulla, poiche’ cos(θ + π) = − cos θ.
41
L’interferenza di due raggi luminosi fu stabilita con una famosa esperienza dovuto
a Young. Una discussione piu’ approfondita verra’ fatta in seguito. Qui basta
ricordare che nell’esperimento due onde (con la stessa frequenza) provenienti da
fenditure diverse vengono fatte incidere su uno schermo. Queste onde sono descritte
da
2π
(x − λνt)
(2.51)
φ(x, t) = A sin
λ
Dato che la x misura la distanza a partire da una data origine, per esempio la
sorgente, il valore della x con cui le due onde arrivano sullo schermo e’ in genere
diverso tra loro. Avremo cosi una differenza di fase a seconda della distanza percorsa.
Segue cosi’ il fenomeno per cui in certe zone dello schermo si hanno dei massimi o dei
minimi di intensita’ (che, ricordiamo, varia con il quadrato del campo e quindi come
il quadrato della somma delle due onde). Infatti, ricordiamo, che il campo elettrico
ed il campo magnetico, sono grandezze vettoriali e come tali si compongono con le
regole della somma vettoriale (si sommano tra loro le componenti).
La direzione del campo elettrico esprime anche la polarizzazione di un’onda
elettromagnetica ed esiste sempre la possibilita’ di decomporre un vettore lungo
due direzioni perpendicolari tra loro e nello stesso piano del vettore. Per esempio
un campo elettrico diretto lungo l’asse delle x ha componenti (E, 0, 0) e lo si puo’
decomporre lungo gli assi x′ e y ′ ortogonali tra loro e, per esempio, a 450 con il
campo, ottenendo
~ = √1 (E, −E)
E
(2.52)
2
dove ora le componenti sono rispetto al nuovo riferimento (vedi Figura 2.7).
x'
y
y'
E
x
~ decomposto lungo gli assi (x′ , y ′).
Figura 2.7: Il campo elettrico E
2.3.3
Il meccanismo della visione
Veniamo adesso ai processi di indagine fisica quali, per esempio, la misura di posizione di una particella. Queste osservazioni vengono fatte, di norma, inviando sul42
l’oggetto in esame delle onde elettromagnetiche. Quello che si osserva e’ il disturbo
prodotto dall’oggetto sull’onda stessa (vedi Figura 2.8). In generale, il meccanismo
consiste nell’invio di un’onda elettromagnetica sull’oggetto che si vuole esaminare.
L’onda viene riflessa dall’oggetto e il nostro occhio, od un rivelatore, osserva l’onda
Sorgente
Oggetto
Osservatore
Figura 2.8: Il meccanismo della visione.
riflessa che contiene le informazioni sull’oggetto che si sta osservando. Per fare una
buona misura di posizione e’ necessario fare uso di onde elettromagnetiche che abbiano lunghezza d’onda piccola rispetto alle dimensioni dell’oggetto. Per esempio,
in Figura 2.9, vediamo che un oggetto piccolo rispetto alla lunghezza d’onda non
produce disturbo, mentre lo produce se e’ grande.
Figura 2.9: L’oggetto a sinistra (piccolo rispetto alla lunghezza d’onda) non produce
disturbo, mentre quello a destra (grande) lo produce.
2.4
Gli inizi della meccanica quantistica
La teoria classica tratta, in generale, sistemi macroscopici per i quali non ci siano problemi nel pensarli rappresentati in termini delle coordinate e delle velocita’.
D’altra parte quando si ha a che fare con corpi microscopici, e quindi al di fuori della
portata diretta dei nostri sensi, il problema cambia radicalmente. Sebbene questo
aspetto sia stato inizialmente ignorato cercando di estrapolare la descrizione classica
43
a queste nuove circostanze, le evidenze sperimentali mostravano che questa estrapolazione non funzionava. La prima indicazione in questo senso venne dal problema
del corpo nero.
2.4.1
Il corpo nero
L’ipotesi dei quanti fu formulata da Max Planck (fisico tedesco) nel 1900 in corrispondenza dei suoi studi sul corpo nero. E’ comune esperienza che un metallo
riscaldato sino all’incandescenza emette radiazioni luminose. Per esempio a 850 0 K
(un po’ meno di 600 0 C) un metallo emette luce rossa. Aumentando la temperatura
si vede il giallo ed il colore si sposta lentamente verso il blu sino a circa 2000 0 K
dove si vede il bianco cioe’ una mescolanza di tutti i colori del visibile. La ricerca di
Planck aveva lo scopo di determinare lo spettro della radiazione emessa da un corpo
incandescente, ma questa radiazione dipende dal corpo che si scalda. Esiste pero’
una situazione ideale, quella del corpo nero, cioe’ un corpo che assorbe completamente le radiazioni che lo colpiscono, per cui la radiazione che emette non dipende
ne’ dalla forma ne’ dalla sostanza del corpo stesso e questo permette una indagine delle proprieta’ intrinseche della radiazione. Un corpo nero si puo’ realizzare,
Figura 2.10: Come si può realizzare un corpo nero.
come mostrato in Figura 2.10, con una scatola chiusa nella quale venga praticato
un piccolo forellino che, in pratica, lascia entrare la luce ma ne fa uscire solo una
piccolissima quantità.
La Figura 2.11 mostra che il risultato del calcolo classico dell’intensità emessa in funzione della frequenza dell’onda elettromagnetica è in contrasto con i dati
sperimentali. Inoltre, dato che il calcolo classico da’ una intensità crescente con
la frequenza, si vede che, integrando su tutte le frequenze per determinare l’intensità totale della radiazione emessa, si ottiene un risultato infinito (catastrofe
ultravioletta), cosa fisicamente assurda. Le curve sperimentali mostrano invece
un andamento che va esponenzialmente a zero per grandi frequenze. All’equilibrio
termico le pareti del corpo nero e la radiazione saranno in equilibrio termico. Si puo’
44
Intensita'
(unita' arbitrarie)
calcolo classico (Rayleigh-Jeans) a T = 2000 0K
T = 2000 0K
T = 1500 0K
T = 850 0K
0
2
4
6
8
frequenza
(unita' arbitrarie)
Figura 2.11: Intensità della luce emessa da un corpo nero in funzione della frequenza
misurata sperimentalmente. La linea tratteggiata (di Raileigh e Jeans) mostra il
risultato del calcolo fatto a partire dalla teoria classica dell’elettromagnetismo.
quindi affrontare il problema cercando di descrivere la materia delle pareti all’equilibrio. Dato che le pareti sono fatte da atomi, cioe’ da nuclei ed elettroni carichi,
queste particelle oscillano con la frequenza stessa del campo a cui sono sottoposte.
Quindi, in un modello molto semplice (ma come detto le proprieta’ del corpo nero
non dipendono dal materiale) le pareti del corpo nero possono essere pensate come oscillatori che vibrano alle frequenze del campo elettromagnetico presente nella
cavita’(vedi Figura 2.12). Dato che questi oscillatori sono carichi e trattandosi di
un moto accelerato (la velocita’ dell’oscillatore cambia durante l’oscillazione) essi
riemettono radiazione elettromagnetica (che corrisponde alla radiazione riflessa).
A
A
t
t= 3/4 T
t=0
t = T/2
t=T
t = T/4
T
Figura 2.12: La figura di sinistra mostra una pallina attaccata a d una molla. Sulla
destra è rappresentata l’ampiezza delle oscillazioni in funzione del tempo.
Il moto di un oscillatore e’ caratterizzato da un’ampiezza A ed un periodo T.
La frequenza dell’oscillatore, cioè il numero delle oscillazioni fatte in un secondo è
45
l’inverso del periodo
1
(2.53)
T
Invece, l’ampiezza dell’oscillazione dipende dall’energia conferita (cioe’ dalla forza
applicata). Secondo la fisica classica l’energia dell’oscillatore puo’ assumere qualunque valore. Se pero’ si ha un insieme di oscillatori ad una data temperatura allora
tutti gli oscillatori hanno mediamente la stessa energia. Dato che si hanno infinite
frequenze l’energia totale del corpo nero risulterebbe infinita (catastrofe ultravioletta). Planck (1900) risolse questo problema assumendo che un singolo oscillatore di
frequenza ν potesse avere solo valori discreti di energia
ν=
E = nhν
(2.54)
dove h è la costante di Planck che ha le dimensioni di un’azione (energia× tempo)
e vale
h ≈ 6.626 × 10−34 J · s.
(2.55)
mentre n è un intero positivo. Inoltre assunse che la distribuzione di energia relativa
ai singoli oscillatori non potesse superare il valore previsto dalla fisica classica, vedi
Figura 2.13. Come si vede il numero di modi di oscillazione possibili diminuisce al
crescere della frequenza, mentre nel caso classico rimane costante. Quindi nell’ipotesi
di Planck la catastrofe ultravioletta viene evitata.
E = hνn
n=5
n=4
n=3
energia classica
n=2
n=1
frequenza
Figura 2.13: La figura mostra il numero di modi possibili per ogni valore di n al
variare della frequenza.
46
2.4.2
Einstein e i fotoni
Einstein in un lavoro fondamentale del 1905 riprendeva l’analisi di Planck del corpo
nero in quanto riteneva che l’idea di identificare la distribuzione di energia della radiazione em all’interno del corpo con la distribuzione di energia degli oscillatori non
fosse corretta, ma piuttosto che si dovesse passare all’idea che la radiazione stessa
fosse quantizzata secondo la formula di Planck, cioe’ che ad ogni radiazione di frequenza ν dovesse associarsi un quanto di energia (il fotone) pari a hν. E’ possibile
che anche Planck avesse avuto un’idea simile ma ritenenendola eretica avesse preferito trasferire la quantizzazione a livello della materia, sulla quale all’epoca ben poco
si sapeva, mentre le proprieta’ della radiazione em che derivavano dalle equazioni di
Maxwell facevano parte del credo dei fisici. L’idea di Einstein era eretica dato che
apparentemente si allontanava dal comportamento ondulatorio della radiazione che
era ben nota dagli esperimenti di diffrazione ed interferenza. Queste ultime proprieta’ discendono direttamente dalle equazioni di Maxwell in cui all’epoca c’era una
fede incrollabile. L’idea rivoluzionaria di Einstein era che la luce possedesse, oltre ad
un aspetto ondulatorio riflesso dalla presenza della frequenza della radiazione nella
formula di Planck, anche un aspetto corpuscolare che si manifestava con l’assorbimento e l’ emissione della radiazione per quantita’ discrete di energia, il quanto hν.
Solo piu’ tardi, nel 1916, mostro’ che al fotone era necessario associare un impulso
dato dalla relazione p = E/c. L’ipotesi del fotone fu confermata sperimentalmente
da Compton nel 1923 che studio’ il comportamento degli elettroni sotto l’azione di
un’onda elettromagnetica e mostro’ che il risultato non e’ in accordo con le idee classiche ma che invece, in tali circostanze, la radiazione elettromagnetica si comporta
come un insieme di corpuscoli.
Dunque, Einstein, contrariamente a Planck, ipotizzava che un campo em in una
cavità si comportasse come un sistema di oscillatori armonici, e che l’energia em
che competeva ad una data frequenza ν fosse dovuta ad un insieme di corpuscoli
indipendenti in numero pari a:
U
n=
(2.56)
hν
dove U e’ l’energia em associata all’onda. In altri termini l’energia dell’onda si
ripartisce tra n corpuscoli (fotoni) ognuno di energia E = hν. In questo modo
l’interpretazione di Einstein del corpo nero era che la luce veniva emessa come un
insieme di fotoni ognuno con energia hν. Applicando questa idea anche all’assorbimento Einstein fu in grado di spiegare in modo semplice l’effetto fotoelettrico.
L’effetto consiste nell’emissione di elettroni da parte di metalli irraggiati con la radiazione e.m.. I principali fatti sperimentali a questo riguardo sono:
1) - esiste una frequenza di soglia ν0 che dipende dal metallo irraggiato.
2) - L’energia cinetica degli elettroni emessi varia tra 0 ed un massimo che dipende
in modo lineare dalla frequenza ν0 , ma non dipende dall’intensità della radiazione.
3) - Il numero di elettroni emessi per secondo e per unità di superficie è proporzionale all’intensità della radiazione.
47
4) - L’estrazione degli elettroni avviene istantaneamente.
La spiegazione classica del fenomeno assume che sulla superficie del metallo ci sia
una barriera elettrica e che gli elettroni siano in pratica liberi all’interno. Per estrarre gli elettroni occorre compiere un lavoro w sufficiente a superare la barriera, detto
lavoro di estrazione. Supponiamo che l’energia incidente sia distribuita in modo
uniforme sulla superficie, occorrerà un certo tempo perché un elettrone accumuli
l’energia sufficiente a superare la barriera. E’ possibile fare un calcolo in condizioni
realistiche sul tempo necessario per l’estrazione e il risultato e’ che occorrono parecchie ore in netto contrasto con gli esperimenti. Inoltre in questo caso la velocità di
emissione degli elettroni dovrebbe essere funzione dell’intensità della luce. Nell’ipotesi dei fotoni si assume invece che l’estrazione avvenga perché il singolo elettrone
assorbe il singolo fotone, cioè con un assorbimento localizzato, il processo risulta
istantaneo e detta K l’energia cinetica massima che può assumere l’elettrone, si ha
hν = w + K
(2.57)
Inoltre all’aumentare dell’intensità aumenterà il numero di fotoni emessi ma non la
loro energia. Questa ipotesi si può verificata. Riportando in un grafico (vedi Fig.
2.14) K in funzione di ν si può determinare sia w che la costante di Planck.
K
tan α = h
α
ν
-w
Figura 2.14: L’energia cinetica degli elettroni misurata nell’esperimento sull’effetto
fotoelettrico in funzione della frequenza
2.4.3
Il problema atomico
All’inizio del 900 molti fisici erano interessati al problema della struttura atomica.
Molti modelli erano stati proposti ma quando nel 1911 Rutherford e collaboratori
48
studiarono l’urto di particelle alpha6 sugli atomi, divenne chiaro che l’atomo doveva
essere costituito da un nucleo centrale, in cui si concentrava in pratica tutta la
massa dell’atomo, e da elettroni esterni, molto piu’ leggeri. Le dimensioni tipiche
atomiche sono dell’ordine di 10−8 cm., mentre quelle del nucleo circa 10−12 − 10−13 .
In linea di principio il problema del moto degli elettroni (carichi negativamente)
nel campo della forza coulombiana generata da un nucleo carico positivamente si
poteva affrontare e risolvere tramite la meccanica classica. In particolare, il caso
dell’atomo di idrogeno, composto da una carica centrale positiva e dall’elettrone
di carica opposta era matematicamente identico a quello del moto di un pianeta
nel campo gravitazionale del sole. Infatti la forza gravitazionale e quella elettrica
dipendono entrambe dall’inverso del quadrato della distanza e danno luogo allo
stesso tipo di equazione differenziale. D’altra parte, anche senza fare molti conti si
capisce il tipo di problema a cui si va incontro. Infatti un elettrone, in analogia ai
pianeti, girera’ attorno al nucleo e quindi si muovera’ di moto accelerato. D’altra
parte la teoria di Maxwell dell’elettromagnetismo ci dice che una carica accelerata
perde energia in modo proporzionale al quadrato della sua accelerazione. Dunque
l’elettrone perde via via energia e corrispondentemente si avvicina sempre piu’ al
nucleo7 . E’ allora semplice vedere che un elettrone che sia inizialmente ad una
distanza dell’ordine del raggio atomico (10−8 cm.) e’ destinato a cadere sul nucleo
in un tempo dell’ordine di 10−11 secondi. Ovviamente questo significherebbe che la
materia come noi la conosciamo non puo’ esistere.
Nel 1908, Walter Ritz scopri’ una semplice proprieta’ delle frequenze della radiazione elettromagnetica emesse da un atomo. Questa proprietà prende il nome di
Principio di Combinazione e dice che tutte le frequenze, ν, emesse da un dato atomo
si possono scrivere nella semplice forma
ν = νn − νm ,
n, m = 1, 2, 3, · · ·
(2.58)
dove le frequenze νn sono caratteristiche dell’atomo considerato. Fu Bohr, nel 1913,
a suggerire che associando ad ogni frequenza ν emessa dall’atomo, l’emissione di un
fotone di energia E = hν, era possibile spiegare il principio di Ritz come conseguenza
della variazione dell’energia dell’atomo dovuta all’emissione (o all’assorbimento) di
un fotone
hν = En − Em
(2.59)
Inoltre Bohr, pur rimanendo nell’ambito della meccanica classica, fece due nuove
importanti assunzioni. La prima fu che non tutte le energie fossero possibili per l’elettrone nell’atomo o, detto in altro modo, che non tutte le orbite di raggio arbitrario8
fossero permesse, ma solo quelle per cui il momento orbitale e’ quantizzato
/,
L = mvr = nh
6
/h =
h
2π
(2.60)
La particella alpha (α) e’ il nucleo dell’elio ed e’ costituita da due protoni e due neutroni
Una buona analogia e’ quella di un satellite artificiale in orbita terrestre che a causa dei vari
attriti perde energia e quindi alla fine cade sulla terra
8
Per semplicita’ considereremo solo orbite circolari
7
49
con m la massa dell’elettrone, v la sua velocita’, r il raggio dell’orbita e h la costante
di Planck. Infine Bohr postulava, contrariamente al risultato classico, che l’elettrone,
ruotando attorno al nucleo, non emettesse energia em, ma emettesse solo quando
l’elettrone passa da un’orbita all’altra. Questa ipotesi fu detta ipotesi degli stati
stazionari, nel senso che un elettrone che si trova nello stato corrispondente ad uno
dei possibili valori dell’energia quantizzata, non puo’ emettere radiazione. Sotto
queste condizioni, ed usando la meccanica classica, si potevano facilmente calcolare
le energie (quantizzate) delle possibili orbite, e nel caso dell’atomo di idrogeno il
risultato era
m e4
(2.61)
En = − 2 2 , n = 1, 2, · · · , ∞
2n /h
con e il valore assoluto della carica dell’elettrone 1, 602 ×10−19 Coulomb. Il risultato
si accordava benissimo con un risultato empirico dovuto a Balmer che dava appunto
le frequenze emesse come
1
1
ν=R
−
, m = 3, 4, · · ·
(2.62)
22 m2
Dunque le ipotesi di Bohr erano in accordo con i dati empirici ed inoltre permettevano il calcolo di R (costante di Rydberg) in termini di costanti fondamentali (m, e, h).
Ovviamente, il problema della instabilita’ atomica non era veramente risolto dalla
teoria di Bohr, ma semplicemente evitato con l’ipotesi delle orbite stazionarie.
2.4.4
La meccanica delle onde e quella delle matrici
Dopo questi successi della teoria atomica di Bohr ci furono ulteriori sviluppi specie
nella generalizzazione al caso delle orbite ellittiche dovuta a Sommerfeld e Watson
(1915), ma i progressi furono lenti, anche perche’ si rimaneva in un ambito di pensiero
eminentemente classico, al quale veniva aggiunto (in modo piu’ o meno arbitrario) un
qualche postulato di quantizzazione. Il passo successivo, piu’ significativo sul piano
concettuale, e’ dovuto a De Broglie nel 1923. Questo passo fu di una importanza
decisiva perche’ in qualche modo buttava a mare l’intera costruzione classica. In altri
termini l’idea di De Broglie non era quella di correggere ed introdurre delle regole
quantistiche all’interno della teoria classica ma, bensi, di costruire una meccanica
su basi concettuali nuove. De Broglie suppose che l’idea di una descrizione duale
della luce in termini corpuscolari ed ondulatori la si potesse estendere anche alle
particelle. Dunque si trattava di associare una descrizione ondulatoria a quella di
particella. De Broglie penso’ che questo si potesse fare lasciandosi guidare dalla
descrizione duale che si da per le onde luminose. Partando dalla relazione che lega
l’energia, E, trasportata da un raggio luminoso monocromatico all’impulso, p della
radiazione stessa9
E = pc
(2.63)
9
La luce esercita su una superficie su cui venga riflessa una pressione di radiazione. La luce
rimbalzando cede una certo impulso alla superficie che a sua volta genera una forza e quindi una
50
possiamo scrivere
E = pc = p(νλ)
(2.64)
dove si e’ usato la relazione tra frequenza e lunghezza d’onda per un’onda luminosa
(λ = c/ν). Ma la relazione di Planck ci dice che
E = hν
(2.65)
hν = p(νλ) ⇒ h = pλ
(2.66)
e quindi
e finalmente la relazione fondamentale di De Broglie
p=
h
λ
(2.67)
Einstein per primo aveva attribuito ai fotoni l’impulso (2.67), ma l’idea di De Broglie
era di associare anche ai corpi materiali di impulso p un’onda con una lunghezza
d’onda pari a h/p. Come si vede l’impulso e’ inversamente proporzionale alla lunghezza d’onda, per cui a particelle di grande impulso sono associate piccole lunghezze
d’onda. Come vedremo nella sezione successiva, un’onda da’ luogo a fenomeni di
interferenza o di diffrazione passando attraverso a delle fenditure, solo se la lunghezza d’onda e’ dello stesso ordine di grandezza delle fenditure stesse. Qualora la
lunghezza d’onda sia piccola tali fenomeni non si manifestano. In tali circostanze un
raggio luminoso ha comportamento molto simile a quello di una particella. A scopo
esemplificativo consideriamo una palla di massa m = 0.5Kg che si muova con una
velocita’ di 3 m/sec. Il suo impulso sara’
p = mv = 0.5 × 3 = 1.5Kg × m/sec
(2.68)
Il valore della lunghezza d’onda associata e’ pari a10
λ=
h
6.626 × 10−34 joule × sec
=
= 4.4 × 10−34 m
p
1.5Kg × m/sec
(2.69)
Quando si fa passare un fascio di luce attraverso un foro (vedi Figura 2.15), la massima deviazione che subisce il raggio luminoso (contrariamente ad un fascio di particelle che passerebbero tirando a diritto) e’ data da un angolo θ che approssimativamente
risulta (per λ << d)
λ
(2.70)
θ≈
d
pressione sulla superficie. Per un’onda monocromatica si verifica facilmente come E e p siano
correlate. Il fenomeno e’ analogo a quello in cui una palla rimbalzando a terra, produce una forza
(pressione) sul pavimento
10
Le dimensioni di h sono quelle di un’azione, quindi energia × t o, [h] = m(ℓ/t)2 × t = mℓ2 /t.
Quindi [h/mv] = ℓ
51
Quindi se consideriamo un foro dell’ordine di 10 cm, cioe’ 0.1m segue
4.4 × 10−34
= 4.4 × 10−33 radianti
(2.71)
0.1
Se assumiamo che la nostra palla continui il suo percorso sino ai confini dell’universo
(le cui dimensioni sono stimate in 1025 m, segue che la deviazione subita e’ pari a
4.4 × 10−8m, cioe’ quasi dell’ordine delle dimensioni atomiche. Dunque per un
oggetto macroscopico gli effetti ondulatori associati all’aspetto ondulatorio della
materia non sono osservabili. Diverso e’ il caso di un elettrone in un atomo. Le
θ≈
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
θ
d
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
xx
Figura 2.15: Il fenomeno della diffrazione
velocita’ tipiche sono dell’ordine di 108 m/sec e la massa dell’elettrone e’ dell’ordine
di 10−30 Kg. Dunque p = 10−22 Kg × m/sec e
6.6 × 10−34
= 6.6 × 10−12 m
(2.72)
10−22
Dunque la lunghezza d’onda dell’elettrone in un atomo e’ dell’ordine di grandezza
delle dimensioni atomiche. In questa situazione l’aspetto ondulatorio non puo’ essere certo trascurato. Una maniera molto semplice per capire le profonde conseguenze
di tutto questo e’ di considerare ancora l’atomo di idrogeno. Supponiamo che l’elettrone faccia un’orbita circolare. In questo caso l’onda associata dovra’ adattarsi
all’atomo stesso. La condizione e’ che si formi un’onda stazionaria e la condizione
geometrica di continuita’ e’ che il diametro della circonferenza percorsa dall’elettrone
sia un multiplo intero di lunghezze d’onda (vedi Figura 2.16)
λ≈
2πr = nλ
(2.73)
Moltiplicando questa equazione per l’impulso dell’elettrone si ha
2πpr = npλ = nh
52
(2.74)
Dunque si trova che il momento angolare dell’elettrone sull’orbita (dato proprio dal
prodotto pr) e’ quantizzato e pari a
/
L = pr = nh
(2.75)
in accordo con la equazione (2.60). Da questa condizione di quantizzazione si ricavano facilmente le energie possibili per l’atomo di idrogeno date nell’equazione (2.61).
Figura 2.16: La quantizzazione dell’atomo di idrogeno secondo De Broglie
La teoria di De Broglie fu confermata nel 1927 in un esperimento di Davisson e
Germer che osservarono la diffrazione degli elettroni sugli atomi di un cristallo. In
pratica la distanza interatomica funge da fenditura e quindi si realizza la condizione
di avere lunghezze d’onda paragonabili a quelle delle dimensioni della fenditura. Il
risultato dell’esperimento e’ mostrato in Figura 2.17.
Il 19 Luglio 1925 Heisenberg pubblico’ un lavoro fondamentale che dette luogo a
quella che fu chiamata la meccanica delle matrici. Heisenberg partiva dall’idea che
in fisica si deve parlare solo di quantita’ osservabili, cioe’ di quantita’ che e’ possibile
misurare. La conseguenza immediata era che non si poteva parlare delle orbite degli
elettroni che nessun esperimento dell’epoca avrebbe mai potuto osservare e misurare.
Le uniche informazioni che si avevano sulla struttura atomica erano le frequenza
della luce emessa dagli atomi e l’intensita’ di queste radiazioni. Quindi Heisenberg
partiva dall’idea che le energie degli elettroni fossero quantizzate e date dalla formula
di Bohr (2.61). Successivamente Heisenberg notava che classicamente la radiazione
emessa dipende dal dipolo elettrico che e’ essenzialmente la distanza dell’elettrone
dal nucleo moltiplicata per la carica dell’elettrone. D’altra parte, nelle ipotesi di
Bohr la radiazione emessa dipende dai due livelli energetici tra i quali l’elettrone
fa la sua transizione. Ovviamente in questa transizione la distanza dell’elettrone
rispetto al nucleo cambia, ma in un modo che dipende dal livello iniziale e finale.
Questo significa che la posizione dell’elettrone durante la transizione non puo’ essere
53
Figura 2.17: La figura di diffrazione ottenuta nell’esperimento di Davisson Germer
determinata. Alla posizione x andra’ sostituito un numero xnm che dipende dai
livelli tra i quali avviene la transizione. In maniera analoga ci si trova costretti ad
introdurre la velocita’ e l’accelerazione dell’elettrone in termini di quantita’ del tipo
ẋnm e ẍnm . Classicamente si hanno le equazioni del moto (nel caso unidimensionale)
ẍ = f (x)
(2.76)
Secondo Heisenberg queste equazioni rimangono valide ma sostituendo alle variabili
numeriche la doppia infinita’ di nuove variabili del tipo xnm . Il problema immediato
che sorgeva era l’interpretazione di f (x) nella (2.76). La soluzione e’ immediata
se f (x) e’ una funzione lineare, come per l’oscillatore armonico. Con una serie di
argomentazioni Heisenberg riusciva a mostrare che se
x → xnm
allora
x2 → x2nm =
X
(2.77)
xnr xrm
(2.78)
r
E’ allora chiaro come si ottengono le potenze successive, per esempio
X
X
x3nm =
x2nr xrm =
xnm xrs xsm
r
(2.79)
rs
e cosi via. Heisenberg noto’ anche che in generale
X
X
(xy)nm =
xnr yrm 6= (yx)nm =
ynr xrm
r
(2.80)
r
Subito dopo il lavoro di Heisenberg, il 27 Settembre 1925, Born e Jordan, notarono che le quantita’ del tipo xnm possono essere pensate come gli elementi di una
54
matrice (che indicheremo con X) e che la regola di prodotto data in (2.78) altro non
e’ che il prodotto righe per colonne di due matrici. Questi autori furono anche in
grado di dimostrare che le matrici associate alle variabili classiche x e p soddisfano
la seguente regola (regola di commutazione)
/
[X, P ]− ≡ XP − P X = ih
(2.81)
Poco piu’ di un mese dopo, il 7 Novembre 1925 Dirac arrivava alla stessa regola di
commutazione per via completamente indipendente. Inoltre Dirac mostrava che la
matrice X (oggi detta operatore di posizione) soddisfa l’equazione
i
Ẋ = − [X, H]
/h
(2.82)
dove H = H(X, P ) e’ l’hamiltoniana espressa in termini delle matrici X e P e
quindi una matrice essa stessa. Dirac notava anche l’analogia che esiste tra questa
equazione e la (2.21), quando si scelga x come variabile dinamica
ẋ = {x, H}
(2.83)
/ con la parentesi di Poise si mettano in corrispondenza il commutatore −i[X, H]/h
son {x, H}. Dirac il 7 Novembre 1925 e pochi giorni dopo, il 16 Novembre, Heisenberg, Born e Jordan lasciarono perdere la strada originale di Heisenberg concentrandosi invece sulla formulazione di una nuova meccanica in cui le variabili di
posizione e di impulso non fossero numeri ordinari ma matrici non commutanti tra
loro. Questi autori fornirono la prima trattazione completa della meccanica delle
matrici.
Il 17 Gennaio 1926 Schrödinger pubblico’ il primo dei suoi lavori in cui riusciva
a dare una formulazione precisa delle intuizioni di De Broglie. Cio’ che Schrödinger
fece fu di scrivere un’equazione analoga, in un certo senso, all’equazione per le
onde elettromagnetiche. Nel caso dello stato stazionario di un atomo di energia En ,
l’equazione soddisfatta dalla funzione d’onda ψn (q) era
∂
/
H q, −ih
ψn (q) = En ψn (q)
(2.84)
∂q
La funzione H(q, p) e’ l’hamiltoniana classica sulla quale Schrödinger effettuava la
sostituzione
∂
/
(2.85)
p → −ih
∂q
Per l’atomo di idrogeno si ha
H(~x, ~p) =
e2
p~ 2
−
2m |~x|
e dunque
~ =−
/ ∇)
H(~x, −ih
55
/h2
e2
2
~
|∇| −
2m
|~x|
(2.86)
(2.87)
L’equazione differenziale che ne risultava era ben nota nella fisica matematica e
non e’ difficile trovare i valori En per i quali esistono soluzioni che si annullano
all’infinito11 . In questo modo Schrödinger ricavo’ la formula di Bohr per le energie
dell’atomo di idrogeno. Il lavoro di Schrödinger ebbe molta risonanza anche perche’
faceva uso di equazioni differenziali, sulle quali i fisici matematici dell’epoca erano
molto preparati, invece di usare un’algebra matriciale di conoscenza non comune.
Inoltre Schrödinger generalizzo’ la sua equazione d’onda al caso non stazionario
∂
∂ψ(q, t)
/
/
ψ(q, t)
(2.88)
= H q, −ih
ih
∂t
∂q
Erwin Schrödinger realizzo’ molto presto che la funzione d’onda per un sistema
di molti elettroni non poteva essere definita nello spazio ordinario a tre dimensioni.
Per esempio, nel caso di due elettroni essa doveva dipendere dalle coordinate di
entrambi e quindi doveva essere una funzione di sei variabili spaziali e del tempo.
Ci si trovava davanti ad una generalizzazione mai vista prima, si aveva a che fare
con oggetti definiti in uno spazio astratto multidimensionale ed inoltre le funzioni
in oggetto assumevano valori complessi, come e’ chiaro dal fatto che in entrambe le
equazioni di Schrödinger, sia la (2.84) che la (2.88), compare esplicitamente l’unita’
immaginaria.
2.4.5
Il significato probabilistico della funzione d’onda
Uno dei problemi della teoria atomica di Bohr era quello relativo al meccanismo di
emissione e di assorbimento dei quanti di luce. Nel 1915-16 Einstein non riuscendo
a trovare questi meccanismi uso’ un metodo statistico per determinare le probabilita’ relative. In questo modo fu capace di ritrovare la formula di Planck per la
radiazione di corpo nero. Rimaneva pero’ l’interrogativo sui meccanismi di base,
cioe’ su cosa provocava questi fenomeni. Un problema analogo si era presentato a
Rutherford nel 1900 quando aveva cercato di formulare una teoria fenomenologica
della radioattivita’. Anche Rutherford fece uso di metodi statistici introducendo la
probabilita’ di decadimento di un nucleo ed il concetto di mezza vita, cioe’ in quanto
tempo una popolazione atomica si dimezza. I due problemi (quello atomico e quello
della radioattivita’) erano molto simili, anche l’emissione da parte di un atomo puo’
infatti essere pensata come una sorta di decadimento. Restava pero’ nell’animo di
Einstein l’idea che questa descrizione fosse provvisoria e che la si dovesse un giorno
sostituire con una spiegazione deterministica al momento in cui si fosse formulata
una teoria adeguata. Come vedremo la risposta della meccanica quantistica e’ che
invece non esiste nessuna spiegazione deterministica dei decadimenti, e che invece la
natura probabilistica dei fenomeni atomici e’ una legge fondamentale della natura.
Nelle considerazioni atomiche esisteva anche un altro elemento di incomprensione
11
Schrödinger pensava correttamente che essendo l’elettrone presente solo in vicinanza del nucleo,
la funzione d’onda correlata dovesse annullarsi all’infinito
56
e cioe’ da dove viene e dove va il fotone al momento dell’emissione o dell’assorbimento. La risposta a questa particolare domanda risiede nella teoria quantistica
della radiazione o piu’ in generale nella teoria dei campi quantizzati che pero’ non
considereremo in questo corso.
Venendo alla questione dell’interpretazione probabilistica della meccanica quantistica, fu Max Born che il 25 Giugno del 1926 (e piu’ compiutamente il mese successivo) scopri’, per primo, il significato empirico della funzione d’onda, che poi dette
luogo all’interpretazione di Copenhagen della meccanica quantistica. Born aveva in
mente le considerazioni di Einstein ed in particolare il fatto che l’energia associata
ad una radiazione di frequenza ν in un dato volume V , dello spazio puo’ essere interpretata come dovuta ad n fotoni di energia hν. Dunque in termini di fotoni l’energia
sara’ data da nhν. Questo significa che nel dato volume ci sono n fotoni. Se l’energia
totale dell’onda (cioe’ quella relativa a tutto lo spazio) corrisponde a N fotoni, allora
n/N e’ la probabilita’ di trovare un fotone nel volume V . Ma la densita’ di energia
e’ proporzionale al quadrato del campo em, e quindi la probabilita’ n/N puo’ essere
calcolata dal quadrato del campo em. Dopo queste considerazioni l’analisi di Born
si concentro’ sul processo di collisione di un elettrone su un atomo analizzandolo
in analogia con la diffrazione dei raggi X. In questo modo arrivo’ a realizzare che
l’elettrone poteva essere in tutti quei punti dello spazio dove la funzione d’onda era
non nulla e che non c’era modo di dire dove esso fosse effettivamente dato che si
trattava di un evento casuale. Quindi Born arrivo’ a teorizzare che la probabilita’,
dP , affinche’ un elettrone si trovi nell’elemento di volume infinitesimo dV fosse data
da
dP = |ψ(~x)|2 dV
(2.89)
Da questa interpretazione seguiva la necessita’ di normalizzare la funzione d’onda,
di richiedere cioe’ che
Z
|ψ(~x)|2 dV = 1
(2.90)
dove l’integrale e’ fatto su tutto lo spazio. Il significato di questa equazione e’ che il
trovare un elettrone in un qualunque punto e’ un evento certo, e quindi la probabilita’
corrispondente deve essere uguale ad uno. Come vedremo successivamente, la scelta
del modulo quadro della funzione d’onda permette di ritrovare molto semplicemente
le proprieta’ di diffrazione e di interferenza mostrate anche dai corpuscoli materiali.
Ovviamente questa interpretazione da’ luogo a un problema concettuale molto
importante. Infatti noi possiamo calcolare la probabilita’ che un elettrone dopo aver
colliso con un atomo vada in una direzione assegnata, ma la teoria non ci offre alcun
elemento per poter dire a priori in quale direzione l’elettrone potra’ andare. Quindi
non possiamo mai dire dove si trovi una particella, possiamo solo dare la probabilita’
che si trovi in un certo punto. Dunque la meccanica quantistica deve essere una
teoria strettamente probabilistica e pertanto atta a calcolare solo ed esclusivamente
le probabilita’ degli eventi. Una situazione, solo apparentemente analoga, esiste
in meccanica statistica. In questo caso si tratta con un numero molto grande di
sistemi elementari ed e’ praticamente impossibile conoscere le condizioni iniziali
57
di tutti questi sistemi che ci permetterebbe di fare delle previsioni completamente
deterministiche. Si e’ dunque costretti ad usare metodi probabilistici, ma questi
sono dovuti ad ignoranza nostra. Invece nel caso della meccanica quantistica una
concoscenza piu’ dettagliata della realta’ fisica e’ imposssibile. Questo fu reso molto
piu’ chiaro dalla formulazione del principio di indeterminazione di Heisenberg (Marzo
1927).
2.4.6
Il principio di indeterminazione
Heisenberg fece un’analisi critica dei processi di misura tenendo conto della dualita’
onda corpuscolo. L’idea era quella di misurare contemporaneamente posizione ed
impulso di un elettrone. Per determinare accuratamente la posizione e’ necessario,
come sappiamo, usare luce con lunghezza d’onda dell’ordine delle dimensioni dell’elettrone, quindi molta piccola. Ma il fotone trasporta un impulso dato da h/λ,
quindi piccola lunghezza d’onda significa grande impulso. Supponiamo di voler misurare contemporaneamente l’impulso dell’elettrone. Dato che per la misura della
posizione necessitiamo di fotoni di grande impulso, l’urto cambiera’ molto l’impulso
dell’elettrone che quindi non potra’ essere determinato con buona approssimazione.
Se vogliamo migliorare questa misura occorre usare fotoni di impulso piccolo, allora
la lunghezza d’onda associata sara’ grande e la misura della posizione non risultera’
molto precisa. Mettendo insieme questi elementi Heisenberg riusciva a dimostrare
che il prodotto delle indeterminazioni sulla posizione, ∆x e sull’impulso ∆px ha un
limite inferiore
/h
(2.91)
∆x∆px ≥
2
Il fatto che il limite inferiore non sia zero significa che non riusciremo mai a conoscere
con infinita precisione (∆x = 0) la posizione di una particella e lo stesso vale per
l’impulso. Questo e’ da contrastare con la meccanica classica in cui si ammette
di poter conoscere con infinita precisione in qualunque istante posizione e impulso
coniugato di una particella. In pratica queste indeterminazioni possono anche essere
trascurabili. Vediamo alcuni esempi. Consideriamo una particella macroscopica di
massa 1 grammo. Supponiamo di aver misurato la sua posizione con una precisione
di un milionesimo di millimetro, cioe’ 10−9 m. Allora
∆v =
/h
10−34
≈
= 0.5 × 10−22 m/sec
2m∆x
2 × 10−3 10−9
(2.92)
Vediamo che per una particella macroscopica gli effetti del principio di indeterminazione sono completamente trascurabili e mascherati dalle incertezze sulle misure
dovute alla nostra strumentazione che molto difficilmente riuscira’ a raggiungere le
precisioni di cui sopra. Molto diversa e’ la situazione per un elettrone in un atomo.
Dato che le dimensioni di un atomo sono dell’ordine di 10−10 m dovremo misurare
la posizione dell’elettrone molto meglio di cosi. Diciamo per esempio ∆x = 10−13 m
58
(cioe’ una precisione percentuale del per mille). Dato che per la massa dell’elettrone
si ha m = 9 × 10−31 ≈ 10−30 Kg, segue
∆v =
/h
10−34
≈
= 0.5 × 109 m/sec
2m∆x
2 × 10−30 10−13
(2.93)
La velocita’ di un elettrone in un atomo e’ tipicamente di 108 m/sec e quindi l’indeterminazione sulla velocita’ dell’elettrone e’ grandissima. Dunque nel caso atomico
il principio di indeterminazione e’ importante ed infatti la fisica classica fallisce completamente e come si capisce risulta molto difficile parlare di traiettoria dell’elettrone
o della sua orbita dato che conosciamo male posizione ed impulso. Esaminiamo infine il cammino di un elettrone in una camera a nebbia che e’ stata per molti anni
un tipico rivelatore di particelle. L’elettrone nel suo cammino ionizza gli atomi che
fungono da nucleo di condensazione e quindi lascia una traccia visibile all’osservatore. Tramite l’analisi di queste tracce e’ possibile determinare posizione e velocita’
dell’elettrone. Come si riconcilia questo con il principio di indeterminazione? La
dimensione tipica delle tracce e’ di circa un millesimo di millimetro, 10−6 m. Si ha
dunque per un elettrone
∆v =
/h
10−34
≈
= 0.5 × 102 m/sec
−30
−6
2m∆x
2 × 10 10
(2.94)
Ma in questi esperimenti la velocita’ degli elettroni e’ in genere superiore a 1/10
della velocita’ della luce, ≈ 3 × 108 m/sec, quindi
0.5 × 102
∆v
=
≈ 0.16 × 10−4
v
3 × 106
(2.95)
Dunque, in base al principio di indeterminazione, possiamo conoscere la velocita’
con una precisione massima di 10−5. In pratica la precisione sperimentale e’ inferiore. In ogni caso il principio di indeterminazione costituisce un ostacolo vero e
proprio all’idea di particelle che si muovono nello spazio descrivendo delle traiettorie,
dato che non e’ possibile determinare contemporaneamente, con infinita precisione,
posizione e velocita’.
2.4.7
Equivalenza della meccanica ondulatoria (Schrödinger) e della meccanica delle matrici (Heisenberg)
Alla fine del 1926 Schrödinger e Dirac mostrarono la relazione tra la meccanica
ondulatoria e la meccanica delle matrici. Prima di tutto osserviamo che esiste una
relazione semplice tra le due equazioni di Schrödinger, quella che descrive onde
stazionarie (2.84) e quella dipendente dal tempo (2.84). Precisamente l’evoluzione
temporale di uno stato stazionario e’ data da
/
ψ(x, t) = e−iEn t/h ψn (x)
59
(2.96)
Allora la relazione tra le funzioni d’onda degli stati stazionari (per esempio gli stati
di energia definita di un atomo di idrogeno) con le matrici introdotte da Heisenberg
per rappresentare le quantita’ x e p e’ data da
Z
Z
∂
∗
∗
/
ψm (x)dx
(2.97)
xnm = ψn (x)xψm (x)dx, pnm = ψn (x) −ih
∂x
Come vedremo queste equazioni hanno una interpretazione matematica molto semplice quando si considerino le funzioni d’onda come elementi astratti di uno spazio vettoriale (infinito-dimensionale) e le variabili dinamiche come operatori che
agiscono su questo spazio.
Queste considerazioni concludono di fatto la parte storica introduttiva. Prima
pero’ di passare alla descrizione vera e propria della teoria, studieremo un caso
particolare, quello dell’esperimento di interferenza di Young, perche’ ci permettera’
di capire molti degli aspetti di questa nuova meccanica.
2.5
L’esperimento di interferenza di Young
L’esperimento che maggiormente mette in risalto gli aspetti fondamentali della meccanica quantistica è l’esperimento di interferenza di Young, o esperimento
della doppia fenditura illustrato in Figura 2.18.
Figura 2.18: Schema del dispositivo per l’esperimento di Young.
In questo esperimento, un raggio luminoso viene scisso in due fasci per effetto
delle due fenditure F1 e F2 producendo una figura di interferenza sullo schermo.
Le frange di interferenza sono dovute ai diversi cammini percorsi dai due raggi che
possono arrivare in fase o in opposizione di fase sullo schermo, producendo dei minimi
o dei massimi di intensità luminosa, come mostrato in Figura 2.19. Tutto questo è
perfettamente spiegabile nell’ambito della teoria ondulatoria della luce. Supponiamo
adesso di analizzare al microscopio vari punti sullo schermo.
60
Figura 2.19: L’esperimento della doppia fenditura di Young dimostra l’interferenza
della luce. Nel grafico (1) è mostrato lo schema dell’esperimento. Nella parte (2)
viene mostrato l’effetto dell’interferenza costruttiva o distruttiva di due onde elettromagnetiche. In (3) viene mostrata la costruzione delle frange di interferenza sullo
schermo di cui è dato il dettaglio nella parte destra della figura
Sulla base dell’ipotesi ondulatoria della luce ci aspetteremmo di osservare delle
distribuzioni uniformi, come mostrato nella parte sinistra di Figura 2.20. Ciò che
invece viene osservato è rappresentato nella parte destra di Figura 2.20. Si vede un
insieme di punti più o meno fitto a seconda della regione di intensità selezionata.
Questo risultato è invece in accordo con la teoria corpuscolare della luce, cioè con
l’ipotesi dei quanti o dei fotoni, per la quale l’assorbimento avviene per quantità
discrete di energia. Una ulteriore osservazione si può fare confrontando tra loro
punti situati nella stessa frangia di interferenza tramite un’ analisi microscopica. Il
risultato è riportato in Figura 2.21. Come si vede il numero di punti osservati è
mediamente lo stesso nei vari casi, ma la distribuzione è diversa e apparentemente
casuale. D’altronde ci si rende immediatamente conto che l’ipotesi corpuscolare
cade subito in gravi difficoltà. Questo si può capire effettuando l’esperimento in tre
condizioni diverse, quali quelle illustrate in Figura 2.22. Nel caso a) si chiude la
fenditura F2 e si osserva una distribuzione continua di intensità con un massimo in
F1 , come mostrato in Figura 2.22. Questo è esattamente ciò che ci si attende dal
punto di vista corpuscolare. Analogamente, se chiudiamo F1 si trova la distribuzione
simmetrica, centrata in F2 . Se invece apriamo entrambe le fenditure, come sappiamo
non si ottiene la curva a+ b di Figura 2.22, cioè la somma delle due curve precedenti,
ma invece si trova la figura di interferenza. Indicando con I le intensità della luce,
61
Figura 2.20: Nella parte destra: cosa si dovrebbe osservare, in base alla teoria ondulatoria, guardando al microscopio le frange di interferenza prodotte nell’esperimento di Young. Nella parte sinistra cosa si osserva realmente al microscopio. Nei
cerchi di sinistra l’osservazione di intensità massima, mentre nei cerchi di destra
l’osservazione di tre zone di debole intensità
Figura 2.21: L’analisi dettagliata di più punti situati nella stessa frangia di interferenza mostra che il numero medio di punti impressionati è lo stesso, ma cambia la
loro distribuzione che appare del tutto casuale.
si ha
Ia+b 6= Ia + Ib
(2.98)
Ovviamente questo non è un problema dal punto di vista ondulatorio dato che nel
caso della radiazione luminosa sappiamo che dobbiamo sommare i campi. Detta A
l’ampiezza del campo si ha
Aa+b = Aa + Ab
(2.99)
e dato che l’intensità luminosa è essenzialmente il modulo quadrato del campo segue
|Aab |2 = |Aa |2 + |Ab |2 + A∗a Ab + Aa A∗b 6= |Aa |2 + |Ab |2
(2.100)
D’altra parte abbiamo anche visto che sul piano microscopico la distribuzione dell’intensità sullo schermo non è ciò che ci si attende dall’ipotesi ondulatoria. Un
62
passo ulteriore si può fare riducendo l’intensità della sorgente. Questo non avrebbe
alcun effetto sul risultato se tutto andasse come previsto dall’ipotesi ondulatorio.
a+b
a
b
F1
F2
Figura 2.22: L’esperimento di Young effettuato in tre condizioni diverse. Nel caso
a) è chiusa la fenditura inferiore, non si hanno frange di interferenza e si osserva un
massimo in corrispondenza della fenditura superiore. Il caso b) è identico al caso a)
eccetto che si scambiano le due fenditure. Nel terzo caso le fenditure sono aperte e
si osservano le frange di interferenza. Sul lato destro della figura sono riportate e le
distribuzioni di intensità ottenute chiudendo la fenditura F2 , caso a), e la fenditura
F2 , caso b). È anche riportata la somma delle due distribuzioni.
Dal punto di vista corpuscolare le cose invece cambiano, dato che al limite si
potrebbe far passare un solo fotone che potrebbe dare una sola immagine sullo
schermo e certamente non produrre una figura di interferenza. In particolare si potrebbe cercare di capire cosa succede mandando una successione di fotoni, uno dietro
l’altro. Con le tecniche odierne questo è un esperimento possibile, ma possiamo invece ottenere lo stesso risultato usando elettroni. Come sappiamo dall’esperimento
di Davisson e Germer anche gli elettroni mostrano un aspetto ondulatorio. Quindi
se si ripete l’esperimento di Young con elettroni ci attendiamo ancora una figura di
interferenza. E questo è proprio ciò che si trova come mostrato in Figura 2.23. In
questo caso possiamo ripetere varie volte l’esperimento utilizzando numeri diversi
di elettroni, come illustrato in Figura 2.24. Vediamo che le frange si formano aumentando il numero di elettroni. Un risultato analogo nel caso della luce è quello
di fotografie effettuate con pellicole poco sensibili (cioè con bassa densità di grani),
oppure ingrandendo una determinata immagine sullo schermo di un computer. Per
63
Figura 2.23: Confronto tra le frange di interferenza ottenute nell’esperimento di
Young con gli elettroni (frange superiori) e con la luce (frange inferiori).
un numero basso di elettroni non si ha una immagine particolare, ma piuttosto una
serie casuale di punti impressionati. Crescendo il numero degli elettroni i punti immagine sullo schermo si infittiscono in determinate zone sino a formare le frange
di interferenza. La distribuzione dei punti, aumentando la statistica, appare quindi
essere pilotata da quelle che sono le leggi dell’ottica ondulatoria. Pertanto, anche
usando elettroni, la loro distribuzione numerica sullo schermo con entrambe le fenditure aperte, na+b , è diversa dalla somma delle distribuzioni con una sola fenditura
aperta, na e nb . Da un punto di vista corpuscolare il fenomeno è chiaramente inspiegabile, dato che il fatto che un elettrone passi da F1 non cambia a seconda che
la fenditura F2 sia aperta o chiusa.
Chiaramente l’interpretazione classica dei fenomeni non può essere mantenuta
a livello microscopico. Prendendo spunto da considerazioni di questa natura Born
arrivò a formulare, come abbiamo gia’ accennato, l’attuale interpretazione probabilistica della meccanica quantistica. Abbiamo detto che la distribuzione dei punti sullo
schermo appare regolata dalle leggi dell’ottica ondulatoria. Sembra allora naturale
assumere che il campo elettromagnetico possa essere pensato come una ampiezza di
probabilità per trovare un fotone in un certo punto. La probabilità si ottiene invece facendo il modulo quadrato. Questo spiega la distribuzione statistica dei punti
sullo schermo e l’interferenza allo stesso tempo. Questo punto di vista può essere
generalizzato agli elettroni e ad altre particelle, associando ad ognuna di esse una
ampiezza di probabilità complessa, o funzione d’onda
ψ(x)
(2.101)
il cui modulo quadro fornisce la probabilità di trovare la particella nel punto x:
P (x) = |ψ(x)|2
64
(2.102)
Figura 2.24: L’esperimento di Young ripetuto usando un numero crescente di elettroni. Da una immagine informe a) ottenuta con 28 elettroni si passa alla figura di
interferenza c) prodotta con 10,000 elettroni .
Ovviamente, come il campo elettromagnetico soddisfa le equazioni di Maxwell, anche le funzioni d’onda delle varie particelle dovranno soddisfare un’equazione che è
quella che regola la distribuzione di probabilità. Questa equazione è l’equazione di
Schrödinger che discuteremo in dettaglio nel seguito. In questa interpretazione probabilistica perde di senso il concetto di traiettoria di una particella: noi non siamo
in grado di dire da dove sia passata la particella, se da F1 o da F2 ma possiamo dare
solo la probabilità di trovarla in un certo punto dello spazio. Occorre menzionare che
esiste un altro punto di vista, completamente equivalente, ed è l’idea della somma
sui cammini di Feynman. In questo caso non si rinuncia all’idea di traiettoria, ma
si cambiano le regole del gioco delle probabilità. Si assume cioè che siano le ampiezze di probabilità a comporsi con le regole della probabilità classica. Per esempio
per due casi esclusivi, come il passaggio da F1 o F2 , si assume che l’ampiezza di
probabilità totale sia
ψa (x) + ψb (x)
(2.103)
dove le due ampiezze corrispondono al passaggio da F1 o da F2 . Pertanto avremo
un effetto di interferenza nella probabilità. Come detto questo punto di vista è
65
completamente equivalente a quello di Born. Il solo problema è che la matematica
associata è assolutamente non banale, e sebbene nei problemi più attuali il punto di
vista di Feynamn sia il più usato, noi affronteremo lo studio seguendo l’approccio
alla Born.
Una cosa che e’ molto importante sottolineare e’ che se pensiamo ai fotoni o agli
elettroni come corpuscoli, si potrebbe pensare di interpretare questo esperimento
dicendo che si ha quella che viene chiamata una miscela statistica. Una miscela
statistica significa, in questo caso, che abbiamo N particelle, con probabilita’ Pa (x)
e Pb (x) di passare da F1 e F2 rispettivamente e di arrivare ad un punto x sullo
schermo. Dunque in ogni punto x arriveranno
N(x) = NPa (x) + NPb (x)
(2.104)
particella. In questo caso la probabilita’ e’ data da
P (x) =
N(x)
= Pa (x) + Pb (x)
N
(2.105)
e non si ha interferenza. L’interferenza e’ dovuta al fatto che il sistema e’ descritto
da una funzione d’onda che e’ data dalla somma di due contributi
ψ = ψa + ψb
(2.106)
con Pi = |ψi |2 e quindi calcolando il modulo quadro si ha un termine misto responsabile dell’interferenza. E’ da notare invece
R che se misuriamo il numero di particelle
che passano da F1 (che sara’ pari a N dxPa (x)), sapremo
con certezza che il nuR
mero di particelle che passano da F2 sara’ dato da N dxPb (x). Dunque la misura
fatta in F1 determina automaticamente il numero di particelle che passano da F2 .
Possiamo anche dire che se non effettuiamo la misura in F1 la funzione d’onda del
sistema complessivo e’
ψ(x) = ψa (x) + ψb (x)
(2.107)
e non e’ possibile distinguere le due parti della funzione d’onda. Se invece misuriamo
le particelle che passano in F1 separiamo il sistema in due parti, una descritta da
ψa e l’altra descritta da ψb . In altri termini la misura cambia lo stato del sistema.
Possiamo anche dire che mentre prima della misura lo stato tiene conto di entrambe
le particelle, dopo la misura in F1 le particelle che passano da F2 perdono completamente memoria della loro relazione con quelle che sono passate da F1 . Questo e’ un
punto di importanza estrema importanza e, come vedremo, dara’ luogo ad uno dei
capisaldi della interpretazione di Copenhagen, il cosi detto postulato di riduzione
della funzione d’onda.
Vorremmo anche sottolinere che l’esperimento della doppia fenditura eseguito
inviando un fotone alla volta e’ stato fatto solo a meta’ degli anni 80 a Parigi.
Quello con elettroni (sempre un elettrone alla volta) da un team giapponese nel
1987. All’inizio degli anni 90 un gruppo tedesco ha usato atomi di elio, mentre
66
all’MIT e’ stato fatto con atomi di sodio. In tutti questi casi i risultati sono stati
identici a quelli qui descritti usando un fascio luminoso.
Nelle due sezioni successive mostreremo altri esempi di collasso del vettore di
stato.
2.6
L’esperimento di Stern e Gerlach
Discuteremo adesso l’esperimento di Stern e Gerlach, concepito nel 1921 da Stern e
poi realizzato dai due nel 1922. Questo esperimento, cosi come quello della doppia
fenditura mostra chiaramente l’insufficienza della fisica classica nel descrivere certi
fenomeni.
L’apparato sperimentale e’ mostrato nella seguente figura 2.25:
z
x
x
x
x
x
x
x
x
x
x
x
x
xxxxxxxxxxxxxxxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
forno
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
x
x
x
x
x
x
x
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
x
x
x
x
x
x
x
x
x
x
x
S
A
fascio atomico
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
xxxx
collimatore
a)
A'
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxx
xxxxxxxxxxxxxxx
x
xxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxxxxxxx
A
b)
A'
Figura 2.25: Disposizione dell’esperimento di Stern e Gerlach in figura a). In figura b) il
particolare del magnete
Degli atomi di argento vengono scaldati in un forno e poi inviati, tramite un
collimatore, al magnete. Il magnete ha una struttura non omogenea. Un atomo di
argento e’ costituito da un nucleo e da 47 elettroni, di cui 46 si possono visualizzare come una nube a simmetria sferica con zero momento angolare. Il momento
67
angolare nucleare puo’ essere ignorato in questa discussione12 . Dunque l’atomo si
comporta come un atomo pesante con un momento magnetico dovuto allo spin (momento angolare intrinseco) del 47-mo elettrone. Il momento magnetico dell’atomo di
argento risulta dunque proporzionale allo spin dell’elettrone. Si dimostra poi che la
disomogeneita’ del campo magnetico lungo l’asse z produce una forza lungo questa
direzione. L’atomo subisce allora una deviazione lungo l’asse z che dipende dall’orientazione del dipolo magnetico rispetto a questo asse. Precisamente e’ deviato
verso il basso se il momento e’ orientato lungo l’alto e verso l’alto se e’ orientato
verso il basso. Per valori intermedi dell’angolo l’atomo subisce deflessioni minori
rispetto a questi casi limite. In altri termini questo apparato e’ in grado di misurare la componente dello spin (a cui il momento magnetico e’ proporzionale) lungo
l’asse z. Dato che gli atomi sono orientati in modo casuale ci aspettiamo che il
fascio atomico possa arrivare in qualunque posizione compresa tra i due casi limite
sopra considerati. Invece cio’ che si osserva sperimentalmente sono due componenti
distinte del fascio. Invece di osservare una fascia continua, si osservano due righe.
Questo fenomeno fu chiamato di quantizzazione spaziale.
Dunque solo due possibili valori della componente dello spin lungo l’asse z sono
possibili, corrispondenti rispettivamente a spin up e spin down che indicheremo con
Sz± . Numericamente risulta
/h
Sz± = ±
(2.108)
2
E’ da notare che l’uso dell’asse z e’ puramente accidentale, potremmo tranquillamente girare l’apparato di 900 e separare ancora due componenti lungo l’asse
y.
Consideriamo adesso degli esperimenti di Stern e Gerlach sequenziali. Il primo
caso e’ rappresentato in Figura 2.26a, dove un primo apparato di Stern e Gerlach,
indicato con SGz separa il fascio in due componenti lungo l’asse z. Successivamente
blocchiamo la componente Sz− e facciamo attraversare la componente Sz+ ancora
uno apparato SGz. In questo caso solo la componente Sz+ emerge dal secondo SGz.
Questo si spiega facilmente, dato che gli spin sono orientati lungo l’asse z dopo il primo SGz passano inalterati attraverso il secondo. Nel secondo caso in Figura 2.26b,
la prima parte dell’apparato e’ identica al caso a), mentre il secondo apparato SGz
e’ sostituito da uno orientato lungo l’asse x, detto SGx. La componente Sz+ viene
separata in due componenti di uguale intensita’ corrispondenti ad una orientazione
dello spin Sx± . Come si puo’ spiegare questo fatto? Si potrebbe pensare che il fascio
Sz+ che emerge dal primo SGz e’ composto al 50% da atomi con Sz+ e Sx+ , mentre
l’altro 50% é costituito da atomo con Sz+ e Sx− . Per vedere come questa spiegazione non sia corretta possiamo effettuare una ulteriore modifica aggiungendo alla
configurazione b) un terzo SGz. Provvediamo inoltre a bloccare la componente Sx−
emergente dall’apparato SGx. Quello che succede e’ che il fascio Sx+ , che per ipotesi
12
Il momento magnetico del nucleo e’ soppresso rispetto a quello dell’elettrone di un fattore
me /mN . Nel caso dell’atomo di idrogeno questo fattore e’ 1/2000 e decresce all’aumentare del
numero atomico
68
+
Sz comp.
+
Sz comp.
a)
forno
SGz
Sz-
xxxxxxxxxxxxxxxxxxxxxxxxxx
SGz
xx
xx
xx
xx
xx
xx
xx
comp.
+
Sx comp.
+
Sz comp.
b)
forno
SGz
Sz
xxxxxxxxxxxxxxxxxxxxxxxxx
SGx
xxx
xxx
xxx
xxx
xxx
xxx
xxxxxxxxxxxxxxxxxxxxxxxxxx
-
S x comp.
comp.
+
Sx comp.
+
Sz comp.
c)
forno
SGz
Sz-
No Sz- comp.
+
Sz comp.
xxxxxxxxxxxxxxxxxxxxxxxxxx
SGx
xxx
xxx
xxx
xxx
xxx
xxx
comp.
xxx
xxx
xxxxxxxxxxxxxxxx
xxx
xxx
xxx
xxxxxxxxx
SGz
-
Sx comp.
xxxxxxxx
-
Sz comp.
Figura 2.26: Tre esperimenti di Stern e Gerlach di tipo sequenziale
non conteneva atomi con polarizzazione di tipo Sz− viene separato in due componenti Sz± di uguale intensita’. Questo risultato mostra che la selezione del fascio
Sx+ da parte dell’apparato SGx distrugge ogni informazione relativa ad Sz . Questo
risultato illustra anche come non sia possibile, in meccanica quantistica, misurare
simultaneamente Sz e Sx .
2.6.1
Analogia con la polarizzazione della luce
L’ esperimento di Stern e Gerlach ha molte somiglianze con gli esperimenti che si
possano fare usando luce polarizzata e dei filtri Polaroid. Un filtro Polaroid e’ una
lamina di cristallo in grado di far passare solo onde elettromagnetiche i cui campi
elettrici sono orientati lungo la direzione del filtro. Ricordiamo che un’onda piana
elettromagnetica che si propaghi lungo l’asse z, corrisponde ad un campo elettrico e
magnetico orientati nel piano (x, y) (perpendicolare alla direzione di propagazione)
ed inoltre i campi sono perpendicolari tra loro. Tramite un filtro orientato lungo
l’asse x (che chiameremo un filtro-x), un’onda comunque polarizzata diventa polarizzata secondo l’asse x, vedi la Figura 2.27. Chiaramente se ruotiamo un filtro-x di 900
orientandolo lungo l’asse y esso diventa un filtro-y. Dopo esser passata attraverso
un filtro-x il campo elettrico dell’onda puo’ essere descritto come
~ = E0 ~x̂ cos(kz − ωt)
E
(2.109)
dove ~x̂ e’ un vettore unitario lungo l’asse delle x. Analogamente un’onda polarizzata
lungo l’asse y avra’ un campo elettrico dato da
~ = E0 ~ŷ cos(kz − ωt)
E
69
(2.110)
x
E
v
z
H
y
Figura 2.27: La disposizione dei campi elettrico e magnetico discussa nel testo
In queste espressioni ω e’ la pulsazione, e k il numero d’onde, legate alla frequenza,
ν, ed alla lunghezza d’onda λ, da
ω = 2πν,
k=
2π
λ
(2.111)
Il legame con il periodo, T e la velocita’ di propagazione (c) e’ dato da
ω=
2π
,
T
c=
λ
ω
=
T
k
(2.112)
Se facciamo passare la luce attraverso un filtro-x e poi attraverso un filtro-y che
siano efficienti al 100%, all’uscita non avremo nessun fascio luminoso (vedi Figura
2.28). Supponiamo adesso di inserire tra il filtro-x ed il filtro y un filtro-x′ con la
direzione x′ che formi un angolo di 450 rispetto all’asse delle x e sempre nel piano
(x, y) (vedi Figura 2.29). Questa volta dal filtro-y esce un fascio di luce, nonostante
che dopo il filtro-x non ci fosse piu’ componente dell’onda polarizzata in questa
direzione. Cioe’, dopo che la luce passa attraverso il filtro x′ e’ del tutto irrilevante
come fosse il fascio dopo il filtro-x.
filtro-x
filtro-y
nessuna luce
Figura 2.28: Due filtri Polaroid ad angolo retto tra loro bloccano completamente il fascio
luminoso
La situazione qui descritta e’ del tutto simile al caso considerato in Figura 2.26c,
se si stabilisce la corrispondenza:
atomi Sz± ⇔ luce polarizzata lungo x, y
atomi Sx± ⇔ luce polarizzata lungo x′ , y ′
70
(2.113)
filtro-x
filtro-x' (45 gradi)
y
filtro-y
x'
y'
x
Figura 2.29: Nella parte superiore i tre filtri x, x′ e y. Nella parte inferiore sono
rappresentate le tre corrispondenti di polarizzazione del fascio
con y ′ la direzione perpendicolare a x′ . Secondo l’elettrodinamica classica la spiegazione relativa e’ data dal fatto che la luce polarizzata lungo l’asse x′ la possiamo
rappresentare nel seguente modo
i
E0 h
E0~x̂′ cos(kz − ωt) = √ ~x̂ cos(kz − ωt) + ~ŷ cos(kz − ωt)
2
(2.114)
cioe’ come una combinazione di due fasci, uno polarizzato lungo l’asse y e l’altro
lungo l’asse x. Quindi quando questo fascio passa attraverso il secondo filtro-y, la sua
componente x viene assorbita, mentre passa la componente y. L’analisi complessiva
ci dice che dopo il primo filtro-x, il fascio puo’ essere visto come una combinazione
lineare di fasci x′ ed y ′. Il filtro-x′ lascia passare solo la componente x′ . A sua
volta, come gia’osservato, questo fascio puo’ essere visto come una combinazione
di polarizzazione x ed y ed il secondo filtro y lascera’ passare solo la componente
y. La corrispondenza che abbiamo stabilito suggerisce che, come la polarizzazione
del campo elettromagnetico puo’ essere vista come un vettore bidimensionale nel
piano (x, y), anche lo stato di spin di un atomo di argento puo’ essere pensato come
un vettore bidimensionale in uno spazio astratto a due dimensioni da considerarsi
distinto dallo spazio ordinario (x, y), Cosi come la polarizzazione lungo x′ e’ vista
come combinazione lineare delle due polarizzazioni x ed y, potremo pensare allo stato
Sx+ dell’atomo di argento come una combinazione lineare degli stati Sz± . Useremo
per questi stati (vettori bidimensionali) la notazione di Dirac |Sz± i. In analogia a
quanto accade per le onde elettromagnetiche ci aspettiamo allora per lo stato Sx+
1
|Sx+ i = √ |Sz+ i + |Sz− i
2
71
(2.115)
Quindi dall’apparato SGx esce una sovrapposizione di stati Sz± . Pertanto, mentre
la componente Sz− verra’ bloccata, la componente Sz+ passera’ inalterata. In questo
modo si riproducono i risultati di Figura 2.26c.
Una questione da esaminare e’ come si possano descrivere gli stati dell’atomo di
argento di tipo Sy± , dato che i due stati Sz± vengono gia’ usati per descrivere Sx± .
Infatti lo stato Sx− e’ dato da
1
|Sx− i = √ −|Sz+ i + |Sz− i
2
(2.116)
che risulta ortogonale a |Sz+ i. La risposta e’ suggerita ancora dalla polarizazione della
luce. Infatti oltre alla polarizzazione x o y la luce puo’ avere anche una polarizzazione circolare. Questa puo’ essere descritta matematicamente usando combinazioni
complesse dei campi lungo x ed y. Senza entrare in troppi dettagli diciamo che e’
possibile stabilire la seguente corrispondenza
atomi Sy+ ⇔ luce polarizzata destrogira
atomi Sy− ⇔ luce polarizzata levogira
(2.117)
In corrispondenza i vettori che descrivono gli stati Sy± in termini di Sz± sono dati da
1
|Sy± i = √ |Sz+ i ± i|Sz− i
2
(2.118)
Dunque lo spazio bidimensionale necessario per descrivere lo spin risulta complesso.
Cioe’ i vettori di questo spazio si costruiscono prendendo combinazioni complesse
dei due vettori di base |Sz± i.
Riassumendo, abbiamo visto che la meccanica quantistica fa uso di ampiezze di
probabilità complesse che si possono sommare tra loro e che devono obbedire una
equazione d’onda, che per la linearità delle ampiezze, deve essere lineare, perchè la
somma di due soluzioni deve essere anch’essa una soluzione. Pertanto la struttura
matematica che emerge da queste considerazioni è, come vedremo meglio in seguito,
quella di uno spazio vettoriale complesso (spazio di Hilbert).
72