RAPPORTI E PROPORZIONI Dato un rapporto si possono ottenere

RAPPORTI E PROPORZIONI
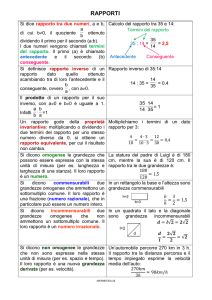
Il rapporto corrisponde all’operazione di divisione.
Il primo termine si dice antecedente, il secondo conseguente.
Un rapporto si può esprimere in tre modi diversi:
Un rapporto si può esprimere in tre modi diversi:
1. Come divisione in riga 2. Come frazione 8
8 : 9
(8 antecedente – 9 conseguente)
9
3. Come quoziente 0,888888
Dato un rapporto si possono ottenere infiniti rapporti equivalenti a quello dato, Dato
un rapporto si possono ottenere infiniti rapporti equivalenti a quello dato
moltiplicando o dividendo antecedente e conseguente per lo stesso numero diverso da zero.
8 16 40 80
9

18

45

90
Il rapporto non può avere il denominatore uguale a zero (zero non può essere divisore!)
Il prodotto tra un rapporto e il suo inverso è uguale a 1.
8 9
x 1
9 8
RAPPORTO TRA GRANDEZZE
Il rapporto tra grandezze omogenee (dello stesso tipo) è un numero puro, cioè un numero senza unità di misura 1.
7cm
 1,4
5cm
10l
2
2.
5l
3.
5,65cm
 2
4cm
Due grandezze omogenee si dicono commensurabili se il loro rapporto è un numero razionale (caso 1 e 2) , incommensurabili se il loro rapporto è un numero irrazionale (caso 3)
irrazionale (caso 3)
Il rapporto tra due grandezze non omogenee potrebbe essere un’altra grandezza e quindi è un numero con la sua unità di misura
quindi è un numero con la sua unità di misura
Es
velocità 
15 Km
 5Km / h
3h
20 Kg
3
densità 

5
Kg
/
dm
4dm 3
SCALA DI RIDUZIONE ‐ SCALA DI INGRANDIMENTO
Il rapporto tra due grandezze si esegue dividendo nell’ordine la seconda diviso la prima. In caso di rapporto tra lunghezze si ottiene una scala.
La scala è di riduzione (carta geografica) se il rapporto è < 1; è di ingrandimento se il
La scala è di riduzione (carta geografica) se il rapporto è < 1; è di ingrandimento se il
rapporto è > 1.
Il rapporto di una scala ha come antecedente la distanza grafica (lunghezza sulla carta) e come conseguente la distanza reale.
scala 
d .grafica
d reale
d.
1
È una scala di riduzione perché il rapporto è<1
È una scala di riduzione perché il rapporto è<1
250
10
scala 
È una scala di ingrandimento perché il rapporto è>1
1
scala 
Solitamente l’unità di misura con cui si esprimono le distanze in una scala è il cm
Formule inverse
d .reale
d .grafica 
conseg
g.scala
d .reale  d .graficaxconsg .scala
Es: Calcola la distanza grafica tra due città che distano 300Km su una carta geografica con scala 1: 1000.
l 1 1000
Dati
d. reale 300Km
300 Km = 30 000 000 cm
Scala 1 : 10 000 000
d .reale
30000000
.
d
grafica

d
.
grafica

 3cm
Distanza grafica?
10000000
conseg.scala
Es : Calcola la distanza tra due città che su una carta geografica con scala 1: 100 000 distano 6 cm
Dati
d grafica= 6cm d. grafica=
6cm
Scala 1 : 100 000
Distanza reale?
d .reale  d .graficaxconsg .scala
d .reale  6 x100000  600000cm
Distanza reale = 600 000 cm = 6 Km
Distanza reale = 600 000 cm = 6 Km