I.T.I.S. "Antonio Meucci" di Roma
Conversione dati (A/D) e (D/A)
a cura del Prof. Mauro Perotti
Anno Scolastico 2009-2010
Conversione dati (A/D) e (D/A)
Sommario
Introduzione ..................................................................................................3
1. Conversione D/A ........................................................................................3
1.1 Il DAC a resistori pesati..................................................................... 5
1.2 Il DAC con rete a scala R-2R (ladder)................................................. 6
1.3 Parametri di un DAC ......................................................................... 8
1.3.1 Offset............................................................................................................. 9
1.3.2 Guadagno...................................................................................................... 9
1.3.3 Linearità ....................................................................................................... 9
1.3.4 Tempo di assestamento.............................................................................. 10
2. La conversione A/D .................................................................................10
2.1 Minimizzazione dell'errore di quantizzazione ..................................... 11
2.2 Osservazioni conclusive ................................................................... 12
3. Architettura degli ADC ............................................................................ 13
3.1 ADC flash (o parallelo) .................................................................... 13
3.2 Gli ADC a retroazione ...................................................................... 13
3.2.1 ADC a gradinata ..........................................................................................13
3.2.2 ADC ad inseguimento ................................................................................ 14
3.2.3 ADC ad approssimazioni successive...........................................................15
4. Parametri e caratteristiche dei convertitori A/D .................................... 17
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
Errori di offset, guadagno e linearità ................................................ 17
Errore di quantizzazione .................................................................. 17
Tempo di conversione ..................................................................... 17
Velocità di conversione.................................................................... 17
Dinamica di ingresso ....................................................................... 17
Impedenza di ingresso .................................................................... 18
Slew rate........................................................................................ 18
Codici mancanti .............................................................................. 18
pag. 2
Conversione dati (A/D) e (D/A)
Introduzione
Le tecniche di conversione di un segnale analogico in digitale (A/D) e di un segnale digitale in analogico
(D/A) sono fondamentali per consentire ad un sistema di elaborazione dati digitale (come un calcolatore,
ma non solo) di interagire con il mondo ad esso esterno.
1. Conversione D/A
Il DAC (Digital Analog Converter) è un sistema che
converte un dato digitale in una grandezza analogica,
generalmente una tensione o una corrente (figura 1). Il
dato digitale, costituito da un certo numero di bit, è
presentato all'ingresso del convertitore in forma seriale o
parallela. L'uscita del sistema è un livello di tensione o di
corrente proporzionale al valore rappresentato dal dato
digitale applicato all'ingresso.
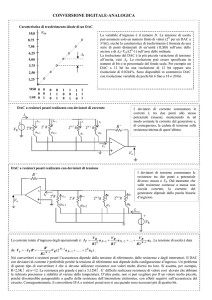
La figura 2 mostra un possibile andamento
dell'uscita di un DAC a 3 bit (il dato digitale
applicato in ingresso è costituito da parole di 3
bit ciascuna). Osservando la figura si possono
fare le seguenti considerazioni:
1.
2.
è richiesto che il dato digitale applicato
all'ingresso sia mantenuto per un certo
intervallo di tempo;
eguali parole binarie producono eguali
livelli della grandezza analogica.
Supponiamo ora, per fissare le idee, che la
grandezza in uscita sia una tensione (Vo) e che
la parola in ingresso (N) sia codificata in
codice binario naturale e sia costituita dagli n bit:
bn-1 bn-2. b1 b0
dove b0 rappresenta il bit meno significativo (LSB) e
scrivere:
(1)
Essendo
quello più significativo (MSB). Potremo allora
Vo = Q · N
Vo ed N
indichiamo con Q.
Ovvero, tra
bn-1
esiste un legame di proporzionalità diretta e la costante di proporzionalità la
N espresso in codice binario naturale, possiamo scrivere:
(2)
N = bn-1 · 2n-1 + bn-2 · 2n-2 + ... + b1 · 21 + b0 · 20
sostituendo quest'ultima espressione nella (1):
(3)
pag. 3
Conversione dati (A/D) e (D/A)
Essendo N un numero puro avremo che Vo e Q dovranno avere le stesse dimensioni. Quindi Q è una
tensione e viene indicata come il quanto della conversione. Moltiplicando e dividendo il secondo membro
n
della (3) per 2 :
(4)
dove
VFS
è la tensione di fondo scala. Nella ricostruzione di una tensione analogica la più piccola
variazione della tensione d'uscita si ha quando cambia solo il bit meno significativo (LSB). Se nella (4)
facciamo cambiare, nella parola
N, solo il bit b0, la variazione di V0 sarà pari a:
(5)
Vo corrispondente al caso in cui tutti i
bit siano pari a zero ed il valore di Vo corrispondente al caso in cui solo il bit LSB sia pari a 1. Nel primo
caso avremo, dalla (3), V0=0. Nel secondo caso, sempre dalla (3), avremo:
Per convincersi di ciò è sufficiente fare la differenza tra il valore di
V0=Q
Se invece cambia solo l'MSB si ha, in uscita, una variazione pari alla metà della tensione di fondo scala.
Anche qui, come per il caso precedente, faremo la differenza tra il valore di Vo corrispondente al caso in
cui tutti i bit sono pari a zero ed il valore di Vo corrispondente al caso in cui solo il bit MSB è pari a 1. Nel
primo caso abbiamo V0=0. Nel secondo caso, dalla (3), avremo:
(6)
dove si è sostituita la (5) in luogo di
Q.
Occorre ora prestare attenzione al fatto che la tensione di fondo scala non corrisponde al valore massimo
assumibile dall'uscita. Questo, infatti, lo si ottiene dalla (3) o dalla (4) ponendo ad 1 tutti i bit:
(7)
Prima di esaminare gli schemi che la letteratura del settore propone per la conversione D/A sono utili
alcune considerazioni.
Come si è visto, la tensione di fondo scala viene divisa in un numero di intervalli che cresce al crescere di
n (il numero dei bit). Contemporaneamente accade che al crescere di n diminuisce anche l'ampiezza
dell'intervallo di quantizzazione Q. Ciò comporta la concreta possibilità di generare segnali di uscita con
andamenti sempre più prossimi a quelli analogici. Per descrivere tale capacità si introduce il parametro
della risoluzione, definito come:
(8)
E' comunque invalso l'uso di indicare la risoluzione di un
DAC con il numero n dei bit di ingresso.
pag. 4
Conversione dati (A/D) e (D/A)
1.1 Il DAC a resistori pesati
La figura 3 mostra un DAC a
resistori pesati ad n bit. Si tratta
di uno schema di importanza
soprattutto
didattica.
I
costruttori,
generalmente,
preferiscono implementare la
soluzione descritta nel paragrafo
successivo per ragioni che si
renderanno evidenti a breve.
Analizzando la figura possiamo
osservare che si tratta di un
sommatore invertente. Si noti,
altresì, la presenza di n deviatori
comandati
dagli
n
bit
di
ingresso. Quando il bit i-esimo
(anche indicato con bi) vale 1 il
relativo deviatore collega il
potenziale -VREF al resistore di
ingresso. Se, invece, bi vale 0, il
relativo deviatore collega al
medesimo resistore il potenziale
di massa.
Il bit più significativo,
R.
bn-1 (MSB),
è collegato, attraverso il proprio deviatore, ad un resistore di valore
bn-2, è collegato, attraverso il proprio deviatore, ad un resistore di
2·R, e così tutti gli altri: al diminuire del peso del bit raddoppia il valore di resistenza del resistore
n-1
associato a tale bit. Il bit meno significativo, b0, è collegato ad un resistore di valore R·2 . Le resistenze
sono quindi pesate secondo opportune potenze di 2 (da cui il nome allo schema).
Il bit immediatamente successivo,
valore
Per l'analisi di tale schema determiniamo le correnti circolanti in ciascuno dei resistori di ingresso. Il
valore della corrente nel ramo associato al bit MSB può essere nullo, se il relativo bit vale 0, oppure
essere pari a -VREF/R, se il relativo bit è pari ad
scrittura possiamo scrivere:
1.
Per rappresentare entrambi i casi con un'unica
(9)
In questo modo se
-VREF/R.
bn-1
è
0 il secondo membro si annulla; se bn-1 è 1 il secondo membro è pari a
In modo del tutto analogo possiamo scrivere il valore delle altre correnti:
...
pag. 5
Conversione dati (A/D) e (D/A)
La somma di tutte queste correnti, che pervengono al nodo (-) dell'A.O., fornisce la corrente
circolando in
I
che,
R, produce la tensione d'uscita:
(10)
I = In-1 +In-2 +...+I0
(11)
v0 = - Rf · I
sostituendo il valore di ciascuna corrente nella (10) e questa nella (11) si ottiene:
(12)
che può essere riscritta nella forma:
Se confrontiamo questa espressione con la (4) possiamo concludere che la tensione di fondo scala è pari
a:
e, applicando la (5), ricaviamo l'espressione per il quanto:
e, dalla (7), l'espressione per il valore massimo assumibile dall'uscita:
Queste tre relazioni definiscono le caratteristiche operative del
DAC a resistori pesati.
Questa struttura circuitale, molto utile da un punto di vista didattico per comprendere il funzionamento di
un DAC, presenta però un fondamentale inconveniente che ne impedisce di fatto la realizzazione: il
valore delle resistenze di ciascun resistore deve essere estremamente preciso: diversamente vengono a
perdere di significato le tre relazioni distintive di questo schema. Si tratta di un vincolo così stringente
che i costruttori preferiscono adottare altre soluzioni come quella della rete ladder descritta nel paragrafo
successivo.
1.2 Il DAC con rete a scala R-2R (ladder)
La rete a scala R-2R, o rete ladder, può assumere differenti tipologie circuitali. Qui viene analizzata
quella maggiormente implementata nelle soluzioni integrate adottate dai principali costruttori (vedi figura
4).
pag. 6
Conversione dati (A/D) e (D/A)
Anche qui, come si può notare, ciascuno degli n bit di ingresso comanda un deviatore che connette il
relativo resistore (di valore 2R) al morsetto (-) dell'A.O., se il relativo bit vale 1; connette invece il
resistore al morsetto (+) se il medesimo bit vale 0. Pur essendo fisicamente diversi entrambi i morsetti,
comunque, si trovano al potenziale di massa. Quindi tutti gli estremi inferiori dei resistori 2R sono
collegati a massa (a prescindere dal valore assunto dal relativo bit).
La particolare simmetria della rete, inoltre, è tale per cui la corrente erogata dal generatore
sempre pari a:
(13)
VREF
è
I = VREF/R
Qualunque sia la disposizione dei bit applicati all'ingresso del DAC. Cerchiamo di
spiegare questa affermazione. Qualunque nodo "vede", alla sua destra, sempre lo
stesso valore di resistenza equivalente. Partiamo dal nodo N0 e poniamoci
immediatamente alla sua sinistra: il resistore equivalente che si vede verso
destra da tale posizione è pari ad R (trattandosi del parallelo di due resistori
eguali e pari a 2R ciascuno - vedi
figura 5). Chiediamoci, ora, che
cosa vede il nodo N1 alla sua
destra: la serie di due resistori
eguali e di valore pari ad R.
Quindi
2R
(vedi figura 6). E così,
anche il nodo N2 vede alla sua destra un resistore
equivalente pari a 2R. Il ragionamento può quindi essere
ripetuto per ciascun nodo fino ad arrivare al primo di
questi, Nn-1, che vede verso destra 2R e verso il basso
2R. Questa catena di ragionamenti giustifica la (13).
VREF, giunta al nodo Nn-1, si divide in due parti eguali:
prosegue verso il nodo successivo Nn-2 (anch'essa pari a I/2).
Proseguiamo nell'analisi. La corrente I erogata da
una scende verso il basso (I/2) e l'altra
Quella che scende verso il basso viene poi dirottata sul morsetto (-) o (+) dell'A.O. sulla base del valore
del bit bn-1. Quella che procede verso il nodo Nn-2 si divide ulteriormente in due parti eguali: una circolerà
verso il basso (I/4) e l'altra verso il nodo
resistore
Rf varrà:
Nn-3
(sempre
I/4).
In definitiva, la corrente che circolerà nel
che possiamo anche riscrivere:
pag. 7
Conversione dati (A/D) e (D/A)
sostituendo ad
I la (13):
da cui la tensione d'uscita:
Anche qui, come abbiamo già fatto per il
la (4) e concludiamo che:
DAC a resistori pesati, confrontiamo quest'ultima relazione con
dove il quanto è stato espresso in valore assoluto trattandosi dell'ampiezza di un intervallo.
In conclusione possiamo affermare che questa configurazione offre, rispetto al
seguenti vantaggi:
•
la rete a scala non pone i problemi del
caso, resistori di due soli valori: R e 2R;
•
la corrente I erogata da
costante;
DAC
DAC
a resistori pesati, i
a resistori pesati dovendosi utilizzare, in questo
VREF è sempre costante e ciò comporta l'impegno di una potenza sempre
i transitori che si verificano in altre soluzioni, in coincidenza
con la commutazione dei bit di ingresso da un livello all'altro,
qui sono praticamente inesistenti in quanto la circolazione
della corrente in ciascun resistore è sempre costante.
1.3 Parametri di un DAC
Vengono qui esaminati i parametri che il costruttore riporta,
per un DAC, nel relativo data sheet. La figura 7 rappresenta
la risposta ideale di un DAC a 3 bit. Questa risposta verrà
considerata quale andamento di riferimento per definire i vari
tipi di errore che affliggono un DAC e che, in definitiva,
modificano la risposta ideale in una risposta reale.
pag. 8
Conversione dati (A/D) e (D/A)
1.3.1 Offset
Consideriamo un DAC unipolare con codice di ingresso binario
naturale. Se all'ingresso applichiamo zero in decimale
(corrispondente ad una sequenza di bit tutti eguali a zero) in
uscita dovremmo rilevare una tensione pari a zero. A causa di
una serie di imprecisioni costruttive tale valore, talvolta, si può
discostare da zero. In tal caso avremmo una risposta come
quella indicata in figura 8. Tale scostamento dal comportamento
ideale viene indicato come errore di offset. Questo errore tende
a mantenersi costante anche in corrispondenza delle altre
sequenze binarie di ingresso. Ciò giustifica l'andamento
parallelo della transcaratteristica rispetto all'andamento di
riferimento riportato in figura 7.
1.3.2 Guadagno
La tolleranza sulle tensioni di riferimento provoca l'errore di
guadagno che si manifesta con una risposta del DAC avente
pendenza diversa da quella ideale (vedi figura 9). Questo tipo di
scostamento viene denominato errore di guadagno.
Sia l'errore di offset che quello di guadagno vengono eliminati
agendo su opportuni piedini di compensazione secondo le
indicazioni riportate sul data sheet del DAC che si sta
utilizzando.
1.3.3 Linearità
Se i punti che definiscono
la caratteristica di un
DAC non si trovano su
una retta, come nel caso
della figura 10, allora
siamo in presenza dell'
errore di non linearità.
Esso è definito come il
massimo scostamento –
in percentuale del fondo
scala o in frazioni di LSB
–
dei
punti
della
caratteristica
reale
rispetto a quella ideale.
Nel caso della figura 11,
ad esempio, si può notare
che tra tutti i punti che
definiscono la caratteristica reale quello che maggiormente si discosta dalla caratteristica ideale è quello
in corrispondenza dell'ingresso 011. Nell'esempio si osserva un valore dell'uscita reale pari a 4.5V
rispetto a quello ideale di
3.0V. In tal modo l'errore di linearità vale, in percentuale del fondo scala:
oppure, in frazioni di
LSB:
(si tenga presente che la tensione di fondo scala si è supposta pari ad
8V
e, di conseguenza, essendo il
DAC a 3 bit, il valore del quanto o dell'LSB è pari ad 1V).
pag. 9
Conversione dati (A/D) e (D/A)
Il costruttore riporta nel data sheet anche l' errore di non
linearità differenziale. Si tratta della massima differenza,
espressa in frazioni di LSB, tra l'incremento reale dell'uscita e
quello ideale in corrispondenza dell'ingresso di 1 LSB. La figura
12 mostra il significato di tale tipo di errore. Si può notare che,
in tale esempio, l'errore di non linearità differenziale ammonta
ad 1.5 LSB.
Nel caso di un errore di
non
linearità
differenziale superiore
ad 1 LSB si ha che
l'uscita può aumentare
o
diminuire di
un
gradino di ampiezza
superiore al quanto (o
ad 1 LSB). Si può verificare, in tale circostanza, la presenza di
un altro tipo di errore: quello di non monotonicità. Si tratta di
una diminuzione del valore dell'uscita reale rispetto al valore
assunto
in
corrispondenza
della
sequenza
binaria
immediatamente precedente (vedi figura 13). Con un errore di
non linearità inferiore a +/- ½LSB si scongiura l'errore di non
monotonicità.
1.3.4 Tempo di assestamento
Questo parametro è indicato dal costruttore con il termine settling
time. E' definito come l'intervallo di tempo necessario all'uscita di un
DAC per raggiungere il suo valore finale all'interno di +/- ½LSB.
Tipicamente il data sheet riporta questo dato rispetto a due
commutazioni tipiche: 1 LSB ed 1 MSB. La figura 14 mostra il
significato di tale errore. In essa si è supposto che in ingresso,
all'istante t1, vi sia stata la commutazione dalla sequenza binaria
011 alla sequenza 100. L'andamento della tensione d'uscita, come si
può notare, non avviene in modo istantaneo ma oscillatorio. Vi è poi
un istante, indicato in figura con t2, a partire dal quale la tensione
d'uscita risulta contenuta all'interno di +/- ½LSB. Il tempo di
assestamento corrisponde proprio all'intervallo di tempo
t2 - t1.
2. La conversione A/D
Il processo della conversione analogico-digitale ha lo scopo di trasformare un segnale analogico (in
genere una tensione) in un insieme di codici digitali. I circuiti che svolgono tale compito, realizzati in modi
differenti, formano la famiglia degli ADC (Analog to Digital Converter).
Il segnale analogico varia all'interno dell'intervallo denominato range di fondo scala. Questo può essere
unipolare, ad esempio da 0V a 5V, oppure bipolare, ad esempio da –15 V a 15 V. Se indichiamo con
VFS l'ampiezza di tale intervallo (5V nel primo esempio e 30V nel secondo) e con n il numero dei bit del
convertitore, definiamo il quanto o intervallo di quantizzazione il rapporto:
(14)
Il range di fondo scala viene quindi diviso in un numero di fasce dipendente dal numero di bit del
convertitore. Per n=3, ad esempio, si avranno 8 fasce. Facciamo un esempio per comprendere meglio. Se
VFS=8V ed n=4 avremo:
pag. 10
Conversione dati (A/D) e (D/A)
questo vuol dire che se la
vi
assume valori compresi tra
0V
e
0.5V il
dato digitale in uscita sarà:
0000;
se la vi assume valori compresi tra 0.5V e 1.0V il dato digitale in uscita sarà: 0001. E così via. In
generale, supponendo il dato digitale in uscita espresso in codice binario naturale, potremo scrivere:
(15)
Il massimo valore codificabile dell'ingresso corrisponderà ad una sequenza binaria di bit tutti eguali ad 1.
In questo caso si avrà:
In figura 15 è riportata la transcaratteristica di un
ADC a 3 bit. Sull'asse delle ascisse vi è la tensione
di ingresso e su quello delle ordinate il dato
digitale in uscita.
Un ADC, quindi, è un circuito che associa un
intervallo di valori della tensione di ingresso ad un
dato digitale in uscita. All'aumentare del numero
di bit diminuisce l'intervallo di quantizzazione e,
nel,contempo,
aumenta
la
precisione
del
convertitore. Viene qui richiamato il concetto di
precisione in quanto l'ADC, nel processo di
conversione, commetterà pur sempre un errore.
Tale errore è detto errore di quantizzazione. Nell'esempio precedente (VFS = 8 V, Q = 0.5 V ed n = 4
bit) se la tensione applicata all'ingresso è pari a 0.22 V il dato digitale prodotto in uscita sarà 0000. Tale
dato verrà interpretato come risultato dell'applicazione, all'ingresso dell'ADC, di una vi pari a 0V. Verrà
quindi commesso, in questa circostanza, un errore di 0.22V (per difetto).
2.1 Minimizzazione dell'errore di quantizzazione
Si può osservare, a questo punto, che il massimo errore di quantizzazione è pari a
figura 15, infatti, si può notare che il dato digitale
000
Q.
Osservando la
è interpretato come una tensione di ingresso pari
a 0V. Tale dato digitale, tuttavia, rappresenta un intervallo di valori pari a Q. Nel caso peggiore,
pertanto, che la reale tensione applicata all'ingresso tenda ad assumere valori verso l'estremo destro
dell'intervallo si avrà, corrispondentemente, un errore di quantizzazione che tenderà ad assumere valori
prossimi a Q.
Per minimizzare tale errore è sufficiente scegliere la
soglia tra un codice di uscita ed il successivo a metà
dell'intervallo di quantizzazione. Si tratta, in
sostanza, di spostare la transcaratteristica indicata in
figura 15 di mezzo quanto verso sinistra. In tal modo
si ottiene la transcaratteristica di figura 16. In questo
modo si avrà che il codice 000 rappresenterà tutti i
valori dell'ingresso compresi tra
001
rappresenterà
tutti
i
0
e
valori
Q/2;
il codice
dell'ingresso
compresi tra Q/2 e 1.5 Q. E così via. In tal modo si
ottiene un errore di quantizzazione, massimo, pari a:
(16)
pag. 11
Conversione dati (A/D) e (D/A)
Va osservato che questa scelta della soglia, che minimizza l'errore massimo di quantizzazione, non
modifica la relazione (15) che rimane comunque valida.
2.2 Osservazioni conclusive
Tenendo conto dell'errore di quantizzazione possiamo affermare che ad un dato codice digitale in uscita,
N0, verrà associato un intervallo di valori della tensione di ingresso:
(17)
Se tutti i bit valgono
0 il bit LSB diverrà 1 quando la vi supererà il valore:
La sequenza corrispondente a tutti i bit eguali a zero tranne l'MSB è stata generata da un intervallo dei
valori della tensione di ingresso:
il valore minimo che la
Il codice digitale
dell'ingresso:
N0
vi deve superare per consentire la commutazione dell'MSB, quindi, vale:
costituito da bit tutti eguali ad 1 è prodotto dal seguente intervallo dei valori
il valore minimo di tale intervallo è:
ciò significa che quando la tensione di ingresso supera tale soglia in uscita si avrà una configurazione di
bit tutti eguali ad 1.
Un'ultima importante considerazione. L'estremo superiore di questo intervallo corrisponde a:
se la tensione di ingresso supera tale valore non si avrà, com'è ovvio, un'ulteriore commutazione del dato
digitale in uscita. In tale circostanza, assolutamente da evitare, ci si troverebbe ad avere una crescita
indefinita dell'errore di quantizzazione.
pag. 12
Conversione dati (A/D) e (D/A)
3. Architettura degli ADC
3.1 ADC flash (o parallelo)
Un ADC parallelo è indicato in figura 17. Come si vede, è
costituito da un determinato numero di comparatori ed una rete
logica del tipo priority encoder. Il numero dei comparatori è
legato al numero n di bit del convertitore dalla relazione:
n°comp = 2n - 1
Il flash illustrato in figura si riferisce al caso di 3 bit (7
comparatori). In esso è anche presente un opportuno partitore
resistivo della tensione
VFS
che ha lo scopo di fissare la soglia
di commutazione di ciascun comparatore. La vi è applicata
simultaneamente sui morsetti + di ciascun A.O. Sappiamo, dal
paragrafo precedente, che per minimizzare l'errore di
quantizzazione la prima soglia di commutazione deve essere
pari a Q/2, la seconda distanziata di Q e le successive
distanziate tra di loro sempre da una quantità pari a Q.
3.2 Gli ADC a retroazione
L'ADC flash è un convertitore molto veloce ma altrettanto costoso. Il suo impiego, pertanto, trova spazio
in tutte quelle applicazioni che richiedono velocità di funzionamento particolarmente spinte (come quelle
in campo video).
Per applicazioni in cui non vi è tale necessità si può
ricorrere ad una categoria di convertitori, detti a
retroazione, di cui la figura 18 mostra l'idea che ne è alla
base del funzionamento.
Una rete logica sequenziale genera e presenta alla sua
uscita tutte le configurazioni binarie possibili secondo un
ordine stabilito dalla strategia implementata in tale rete.
Ognuna di queste configurazioni viene quindi applicata
all'ingresso di un DAC che le trasforma in analogico (vD).
La tensione così prodotta viene confrontata con la
tensione incognita, vi, per mezzo di un comparatore.
Quando l'uscita del comparatore cambia stato la rete logica interrompe la generazione delle sequenze
binarie e salva quella corrente che, nei limiti della risoluzione del convertitore, rappresenta la conversione
in digitale della tensione vi.
3.2.1 ADC a gradinata
Rappresenta il convertitore più semplice e più intuitivo di
questa categoria. La figura 19 ne illustra lo schema
elettrico. La rete logica sequenziale è costituita, in questo
caso, da un contatore binario che produce le configurazioni
digitali in binario naturale in ordine crescente. Queste
configurazioni sono applicate quindi all'ingresso di un DAC
la cui uscita, che indichiamo con vD, è costituita da una
pag. 13
Conversione dati (A/D) e (D/A)
tensione a gradinata crescente (vedi figura 20). La
vD viene quindi confrontata con la tensione
incognita, vi, grazie ad un comparatore ad anello
aperto. L'uscita di questo comparatore è applicata
ad uno dei due ingressi di una porta AND. L'altro
ingresso di tale porta è costituito da un segnale di
clock. Quando vD > vi l'uscita del comparatore si
porta a livello basso e con essa l'uscita della porta
AND. A questo punto si interrompe il conteggio
del contatore. Il dato è quindi pronto per essere
prelevato dal blocco successivo.
Il problema principale di tale convertitore è la sua
particolare lentezza. Non sapendo, infatti, quando
verrà interrotto il conteggio, in quanto tale evento
non è in alcun modo prevedibile, il tempo di
conversione sarà pari al tempo impiegato dal contatore per generare tutte le sequenze. Ovvero:
(18)
dove con TCK si è indicato l'intervallo di tempo tra due fronti attivi del segnale di clock e con n il numero
di bit del convertitore.
3.2.2 ADC ad inseguimento
Questo
1.
2.
ADC è ottenuto da quello appena esaminato grazie a due variazioni:
sostituzione del contatore in avanti con uno UP/DOWN;
controllo della direzione del conteggio per mezzo dell'uscita del comparatore.
La figura 21 mostra lo schema di questo ADC.
Esso può funzionare in free running: ciò significa
che, una volta attivato, aggiorna continuamente il
dato digitale in uscita senza la necessità di fornire
ulteriori comandi.
Non è possibile fornire il tempo di conversione di
questo ADC. E' invece opportuno definire il
massimo slew rate ammissibile dalla tensione vi.
Con ciò si intende la massima variazione del
segnale di ingresso che l'ADC è in grado di
seguire senza sganciarsi dal segnale vi. Dal
momento che l'uscita del convertitore può al
massimo variare di un quanto, ogni periodo del segnale di clock, si avrà che il massimo slew rate
ammissibile dalla vi dovrà rispettare la condizione:
(19)
E' utile osservare, in conclusione, che il valore
iniziale assunto dalla vD è pari alla metà della
tensione di fondo scala: ciò per ridurre i tempi
iniziali (medi) di aggancio. In figura 22 vi è una
possibile situazione di operatività del convertitore.
E' anche rappresentato il caso in cui il convertitore
si sgancia dalla tensione di ingresso in quanto
pag. 14
Conversione dati (A/D) e (D/A)
quest'ultima varia troppo rapidamente.
3.2.3 ADC ad approssimazioni successive
E' tra i convertitori più usati in quanto consente di ottenere brevi tempi di conversione a fronte di una
struttura circuitale abbastanza semplice. La
figura 23 mostra lo schema di questo
convertitore che rispetta, come per i
precedenti due, la logica di funzionamento
degli ADC a retroazione. La principale
differenza è costituita dall'architettura della
logica sequenziale di controllo formata da
un registro ad approssimazioni successive
(S.A.R.). Il funzionamento di questo
registro è basato sul noto algoritmo di
ricerca binaria (molto usato in informatica
per cercare un elemento all'interno di una
lista ordinata). Nel nostro caso si tratta di
cercare in quale quanto cade il valore della
tensione incognita di ingresso.
La conversione ha inizio quando viene
attivato il segnale SOC (Start Of Conversion). Successivamente viene caricata nel S.A.R. una parola
binaria di bit posti tutti eguali a zero tranne l'MSB. Tale parola viene convertita dal DAC in vD e
vi. Se vD < vi la logica di controllo mantiene ad 1 l'MSB e pone ad
1 il bit immediatamente successivo (bn-2). Se invece vD > vi la logica di controllo pone il bit MSB a zero
e, comunque, porta ad 1 il bit immediatamente successivo (bn-2). Tale parola viene quindi passata al DAC
che la converte in vD; successivamente avviene il confronto con la tensione incognita vi. Sulla base
confrontata con la tensione incognita
dell'esito di tale confronto avremo:
•
•
bn-2 = 1 se vD < vi
bn-2 = 0 se vD > vi
Il processo si ripete fino al bit LSB. In questo modo occorreranno n cicli di clock per l'esecuzione
dell'intera conversione più un altro ciclo per le varie operazioni di lettura del dato digitale, inizializzazione
di una nuova conversione, ecc.. Quindi:
(20)
In figura 24 è descritto un esempio di
funzionamento di questo ADC. Si fa
l'ipotesi di VFS = 10 V ed n =
Calcoliamo il valore del quanto:
8 bit.
La prima soglia di commutazione, per
le note ragioni di minimizzazione
dell'errore di quantizzazione, sarà
posta a Q/2 = 19.55 mV. La soglia
successiva sarà distante Q da questa e
così via per tutte le altre.
pag. 15
Conversione dati (A/D) e (D/A)
In figura 25 sono mostrate le prime soglie
(delle 255 complessive).
Supponiamo che la tensione incognita da
convertire sia pari a 5.75 V. Per vedere in
quale intervallo cade applichiamo la formula:
(21)
(10010011)
dove con le parentesi quadre chiuse superiormente ed aperte inferiormente si è indicata l'operazione di
approssimazione all'intero superiore (parte intera superiore).
Il 147° intervallo, di ampiezza
Q=39.1
mV, è indicato in figura 26.
Si può osservare che la vi cade proprio in
tale intervallo (più precisamente nella
prima metà di questo). Seguiamo ora il
processo di conversione così come
descritto nella figura 24.
Avviato il processo di conversione
(attivando la linea SOC) nel SAR viene posta la configurazione 1000000 che viene passata al DAC e
convertita in:
vD =128 Q = 128 · 39.1 · 10-3 = 5.0048 V
Essendo vD <
convertita in:
vi
il convertitore salva l'MSB. La configurazione successiva è:
11000000
che viene
vD =192 Q = 192 · 39.1 · 10-3 = 7.5072 V
Essendo vD >
convertita in:
vi
il convertitore non salva il bit
b6.
La configurazione successiva è:
10100000
che viene
vD =160 Q = 160 · 39.1 · 10-3 = 6.256 V
per cui anche
b5 non viene mantenuto. Si passa alla configurazione: 10010000 convertita dal DAC in:
vD =144 Q = 144 · 39.1 · 10-3 = 5.6304 V
questa volta il bit
b4 viene salvato. Si passa quindi alla configurazione: 10011000 convertita dal DAC in:
vD =152 Q = 152 · 39.1 · 10-3 = 5.9432 V
che essendo maggiore di
10010100, convertita in:
vi
non produce il salvataggio di
b3.
Si pone quindi ad 1 il bit
b2
ottenendo:
vD =148 Q = 148 · 39.1 · 10-3 = 5.7868 V
pag. 16
Conversione dati (A/D) e (D/A)
vD > vi e il
10010010 convertita dal DAC in:
Anche in questo caso
convertitore non salva il bit
b2.
Si passa quindi alla configurazione:
vD =146 Q = 146 · 39.1 · 10-3 = 5.7086 V
vi produce
10010011, convertita dal DAC in:
che essendo inferiore a
il salvataggio di
b1.
Si perviene, quindi, all'ultima configurazione:
vD =147 Q = 147 · 39.1 · 10-3 = 5.7477 V
che essendo inferiore a
vi
produce il salvataggio di
b0.
Tale configurazione è quindi disponibile in uscita
all'ADC per la lettura da parte del blocco successivo.
4. Parametri e caratteristiche dei convertitori A/D
I parametri di funzionamento di un ADC sono descritti nei data sheet dei relativi costruttori ed
informano il progettista sui limiti di funzionamento (massima potenza dissipabile, resistenza d'ingresso,
massima variazione della tensione di ingresso, ecc.) di questi dispositivi.
4.1 Errori di offset, guadagno e linearità
Ciascuno di questi errori, analogamente a quanto già visto per i DAC, descrive lo scostamento del
comportamento reale rispetto a quello ideale. I grafici che mostrano questi effetti si ottengono da quelli
visti per i DAC invertendo, tra loro, le variabili degli assi cartesiani. Anche in questo caso sono possibili
le compensazioni degli errori di offset e di guadagno. Compensazioni che, invece, non sono previste per
gli errori di linearità e di linearità differenziale.
4.2 Errore di quantizzazione
Sappiamo che l'ADC non può generare in uscita un codice in corrispondenza di ciascuno degli infiniti
valori della tensione applicata all'ingresso. Ciò significa che nella codifica del segnale di ingresso viene
introdotto un errore. Si tratta dell' errore di quantizzazione. Per minimizzare tale errore, riducendolo a ±
1/2 LSB, si fissa la soglia di commutazione da un codice al successivo a metà dell'intervallo di
quantizzazione. Il costruttore indica, nel proprio data sheet, la modalità operativa per ottenere ciò.
4.3 Tempo di conversione
Il conversion time è il tempo che l'ADC impiega per effettuare la conversione, in digitale, della tensione
analogica applicata al suo ingresso (tconv).
4.4 Velocità di conversione
Viene misurata in Hz ed indica il numero di conversioni eseguite nell'unità di tempo. Per la sua misura si
tiene conto di tutti i ritardi intrinseci dell'ADC. Il costruttore indica questo parametro con il nome di
conversion rate.
4.5 Dinamica di ingresso
Per garantire il corretto funzionamento dell'ADC (ed anche la sua non distruzione fisica) è necessario
che la tensione analogica applicata all'ingresso sia contenuta all'interno di un intervallo denominato input
voltage range.
pag. 17
Conversione dati (A/D) e (D/A)
4.6 Impedenza di ingresso
Il progettista deve prendere in considerazione tale parametro quando collega l'ingresso dell'ADC
all'uscita del blocco precedente (generalmente si tratta del circuito di condizionamento di un trasduttore).
E' un valore che negli ADC commerciali varia da qualche kΩ a qualche centinaio di MΩ.
4.7 Slew rate
Questo parametro è definito come la massima variazione della tensione analogica d'ingresso, nel tempo,
che consente la fornitura, in uscita, di codici corretti.
4.8 Codici mancanti
ADC a retroazione, nei quali è presente un DAC, si può presentare l'errore dei codici mancanti. Si
tratta dell'impossibilità, da parte dell'ADC, di generare in uscita il corretto codice in corrispondenza di
Negli
uno o più valori della tensione analogica applicata all'ingresso. La ragione di questa impossibilità è dovuta
all'errore di non monotonicità del DAC interno. Per fare un esempio di codice mancante consideriamo
l'ADC a gradinata di figura 19 (pag. 13) ipotizzando, per semplicità, che il numero di bit sia pari a 3.
4V. In tal modo avremo un quanto pari a 0.5V.
2.1V. La corretta codifica dovrebbe fornire la
sequenza 100. Infatti, dalla (17), abbiamo che in corrispondenza di tale sequenza si ha, per la vi:
Supponiamo, inoltre, che la tensione
VFS
sia pari a
Supponiamo, ancora, che la tensione incognita valga
vi = Q · N0 ± εmax = 0.5 · 4 ± 0.25 [V]
a tale sequenza, pertanto, corrisponde un intervallo di
valori per la vi compreso tra 1.75 e 2.25. Supponiamo che
il DAC interno sia caratterizzato da una transcaratteristica
ideale come quella di figura 27 (si noti la sopraelevazione
di mezzo quanto di tutta la curva, necessaria per situare le
soglie tra i codici di uscita a metà degli intervalli di
quantizzazione); quando il contatore binario raggiunge la
sequenza 100 e la passa all'ingresso del DAC questi, alla
sua uscita, fornirà una tensione pari a 2.25V. In quel
momento il comparatore passerà dal livello alto a quello
basso e si interromperà il conteggio.
Se invece la transcaratteristica del DAC è quella di figura
28 (nella quale si nota un errore di non monotonicità) si
può osservare che la tensione in uscita dal DAC in
corrispondenza della sequenza 100 applicata all'ingresso
è inferiore a quella che nominalmente si dovrebbe avere
2.25V). L'uscita del comparatore si manterrà, pertanto,
al livello alto e si dovrà attendere la sequenza
successiva, 101, per avere l'interruzione del conteggio.
La sequenza 100, quindi, non si verificherà mai: è,
appunto, una situazione di codice mancante.
pag. 18