Lezione: Temperatura e calore

Lezione: Temperatura e calore
1
Equilibrio termico e principio zero della termodinamica
Per definire quantitativamente e correttamente dal punto di vista scientifico i
concetti, in gran parte intuitivi e familiari, di calore e temperatura rimanendo
nell’ambito della descrizione macroscopica, non si può fare a meno di ricorrere,
almeno inizialmente, a nozioni soggettive. In particolare alla percezione sensoriale umana di “caldo” e “freddo”, relativa a un corpo o a una porzione di
sostanza”
Innanzitutto possiamo vedere che, per quanto soggettiva, la percezione di
“caldo” o “freddo” è per la maggior parte di noi abbastanza coerente – nel senso
che ci mette grosso modo tutti d’accordo – per quanto riguarda il decidere se un
corpo è più o meno freddo di un altro, o se un corpo dopo un certo intervallo di
tempo è diventato “più caldo” (si è riscaldato) o “più freddo” (si è raffreddato)
di prima.
Partendo da queste considerazioni iniziali si può cominciare a trovare un
punto di partenza osservando che quando due corpi che ci appaiono inizialmente
uno “più caldo” e l’altro “più freddo” vengono messi a contatto, quello più
caldo “si raffredda” e quello più freddo si “riscalda”, fino al raggiungimento di
un equilibrio (detto equilibrio termico) dopo un tempo più o meno lungo. Una
volta raggiunto l’equilibrio termico i corpi cessano di raffreddarsi o riscaldarsi. È
intuitivo che nel processo i due corpi si siano scambiati “qualcosa”: chiameremo
questo qualcosa calore, e ne daremo una definizione più quantitativa tra poco.
Il principio zero della termodinamica, preso come postulato, afferma che
se un corpo A è in equilibrio termico con il corpo B, e il corpo B è in equilibrio
termico con il corpo C, allora A è in equilibrio termico con il corpo C.
Può sembrare un principio ovvio (è l’enunciazione della proprietà transitiva
di una relazione di equivalenza) ma in realtà non lo è, visto che la definizione che
abbiamo dato di equilibrio termico implica il contatto (prolungato) tra i corpi in
questione. Grazie il principio zero della termodinamica possiamo affermare che
i corpi A e C sono in equilibrio termico tra loro anche se non sono mai venuti a
contatto diretto.
2
Temperatura
Diciamo che due corpi macroscopici all’equilibrio termico hanno (per definizione)
la stessa temperatura. Questo però non ci aiuta a darne una definizione quan1
titativa, perché non sappiamo ancora come misurare questa nuova grandezza in
maniera univocamente definita.
2.1
Dilatazione termica
Ci viene in soccorso l’osservazione che in molti materiali (metalli, liquidi, gas)
si verifica il fenomeno – misurabile – della dilatazione termica: il volume di una
data porzione di sostanza aumenta quando la sostanza si riscalda, diminuisce
quando si raffredda.
Per i solidi e i liquidi queste variazioni sono piuttosto piccole (∆V /V 1)
ma si possono amplificare usando speciali accorgimenti tecnici.
Un’ampolla che termina in un tubicino capillare di sezione molto più piccola
di quella dell’ampolla stessa, per esempio, se viene riempita completamente
di liquido in modo che la superficie libera sia all’interno del capillare, riesce a
rilevare piccole variazioni di volume del liquido attraverso variazioni apprezzabili
dell’altezza raggiunta dal liquido stesso nel tubicino.
Δh
ΔV = SΔh
Figura 1: termometro ad ampolla
La variazione di volume ∆V è infatti in questo caso ∆V = S∆h. Se per
esempio l’ampolla ha un volume V = 1 cm3 e il capillare ha una sezione S =
0, 25 mm2 , un ∆h = 1 cm corrisponde a ∆V = 2, 5 × 10−3 cm3 , con ∆V /V =
2, 5 × 10−3 .
Confrontando il comportamento di materiali diversi ci si rende conto che,
almeno per piccole variazioni percentuali di volume il fenomeno è lineare: se
∆V /V raddoppia o si dimezza per un materiale, raddoppia o si dimezza anche
per tutti gli altri che esibiscono il fenomeno della dilatazione termica.
Questo rende possibile sfruttare il fenomeno suddetto per definire in modo
quantitativo (arbitrario) la temperatura, usando un tubicino graduato in un
termometro ad ampolla dalle caratteristiche prestabilite e fissando convenzionalmente in maniera uguale per tutti la scala riportata sul tubicino come scala
di temperatura.
Punti fissi e scala Celsius Grazie a questi termometri arbitrari, si constata
sperimentalmente che alcuni fenomeni avvengono a una temperatura (tacca sul
termometro) ben definita e sempre uguale. In particolare questo è vero per
2
passaggi di stato dell’acqua da solido a liquido (fusione) e da liquido a vapore
(ebollizione) a pressione atmosferica fissata.
Si possono usare questi risultati sperimentali per fissare in maniera riproducibile e uguale per tutti la scala di temperatura: segnando su un termometro le
temperature corrispondenti all’equilibrio termico del termometro in una miscela
di acqua e ghiaccio (presa come 0 della scala), e quella all’equilibrio termico in
un aperto con acqua in ebollizione alla pressione atmosferica di circa 1 atm, e
suddividendo l’intervallo cosı̀ ottenuto in 100 parti uguali si ottiene la scala Celsius o centigrada (un grado Celsius si indica con 1◦ C: la temperatura di fusione
del ghiaccio è dunque 0◦ C, quella di ebollizione dell’acqua a livello del mareo
100◦ C). Dagli stessi due punti fissi, ponendo la temperatura del primo a 32 e
quella del secondo a 212 si ottiene la scala Fahrenheit, ancora usata nel mondo
anglofono.
Coefficienti di dilatazione termica Avendo stabilito un metodo e un’unità
di misura della temperatura, si può descrivere in maniera quantitativa anche il
fenomeno della dilatazione termica.
Ogni materiale che presenta il fenomeno sarà quindi caratterizzato da un
coefficiente di dilatazione termica volumica α tale che
∆V
= α∆T
(1)
V
◦
Per esempio nel caso del rame si ha αCu ≈ 1, 7 × 10−5 C−1
Se l’oggetto che subisce la dilatazione termica è un corpo solido, può capitare
che le sue dimensioni non siano dello stesso ordine di grandezza nelle tre coordinate, e che una o due risultino di fatto trascurabili, o tali che il loro aumento sia
impercettibile per la sensibilità degli strumenti di misura. Esempi sono un foglio
o una lastra sottile di metallo, o una sbarra (per esempio un binario ferroviario)
in cui le dimensioni trasversali siano molto minori di quelle longitudinali.
In questi casi risulta difficile misurare una variazione percentuale di volume,
ed è più comodo misurare la variazione di lunghezza o di superficie. Vengono
perciò definiti, in maniera del tutto analoga a quello volumico, i coefficienti di
dilatazione termica lineare e superficiale:
∆S
= β∆T
S
∆L
= γ∆T
L
I coefficienti α, β e γ sono legati per la maggior parte dei materiali da una
semplice relazione.
Nell’ipotesi che il solido dilatandosi rimanga simile (dal punto di vista geometrico) a sé stesso, abbiamo infatti che per un parallelepipedo di lati a, b, c e
volume V = abc, in corrispondenza a un certo aumento di temperatura si avrà
per definizione di similitudine
∆b
∆c
∆a
=
=
≡ γ∆T
a
b
c
Se per esempio b a e c a la variazione che riusciamo a misurare meglio
(o l’unica che riusciamo a misurare) è ∆a, dunque ci fa comodo conoscere il
3
coefficiente di dilatazione lineare γ per misurare ∆T , oppure per stimare ∆a
dati γ e ∆T (per esempio per calcolare di quanto si può allungare un binario
ferroviario dato il massimo ∆T a cui è sottoposto)
Il nuovo volume sarà
∆b
∆c
∆a
0
1+
1+
V = (a + ∆a)(b + ∆b)(c + ∆c) = abc 1 +
a
b
c
da cui
∆V
∆a
∆b
∆c
=1− 1+
1+
1+
= 1 − (1 + γ∆T )3
V
a
b
c
se le variazioni percentuali sono piccole, come è vero in genere per i solidi,
possiamo usare l’approssimazione di Taylor al prim’ordine
(1 + )3 ≈ 1 + 3
trovando
∆V
≈ 3γ∆T
V
da cui
α = 3γ
Con lo stesso procedimento, calcolando la variazione della superficie S = ab
si trova
∆S
≈ 2γ∆T
S
e quindi
β = 2γ
Dilatazione termica dei gas perfetti
Il caso dei gas, nel caso in cui siano sufficientemente rarefatti da poter essere
considerati gas perfetti è particolarmente interessante perchè sono descritti tutti
dalla legge di Gay-Lussac: a pressione costante
V (T ) = V0 (1 + αT )
dove, se T è misurata in gradi centigradi, il coefficiente α è lo stesso per tutti
i gas e vale
α≈
1
273.5◦ C
Per un gas mantenuto a volume costante vale una legge analoga per la
variazione della pressione con la temperatura
p(T ) = p0 (1 + αT )
4
dove il coefficiente α è di nuovo universale ed è lo stesso che compare nella
legge di variazione del volume.
Per T = −273.15◦ C (lo zero assoluto) il volume del gas a pressione costante (o la pressione a volume costante) si annulla, ed è chiaro che temperature
inferiori non hanno senso, se le equazioni devono continuare a valere.
Le due leggi suggeriscono di cambiare l’origine della scala delle temperature introducendo la temperatura assoluta misurata in kelvin (1K = 1◦ C),
spostandola allo zero assoluto.
Dunque per ottenere la temperatura assoluta basta aggiungere 273.15 K al
valore di T espresso in gradi centigradi:
T(K) = T(◦ C) + 273.15
Le leggi di Gay-Lussac per pressione e volume, e quella di Boyle (pV =
costante fissata la temperatura) si riassumono nella legge dei gas perfetti
pV = nRT
che discuteremo meglio in seguito, in cui n, il numero di moli, è una misura della
quantità di gas, R è una costante universale, dunque indipendente dal tipo di
gas, e T è la temperatura assoluta del gas, definita come sopra.
3
Capacità termica e calore specifico
Si osserva sperimentalmente che per molte categorie di materiali se si mettono a
contatto tra loro due corpi a temperature diverse T1 e T2 , mantenendoli isolati
termicamente da altri corpi e dall’ambiente esterno, la temperatura che essi
raggiungono all’equilibrio è una media delle due temperature iniziali, pesata
con coefficienti che chiamiamo capacità termiche:
Tf =
C1 T1 + C2 T2
C1 + C2
Se i due corpi sono della stessa sostanza, risulta che la capacità termica
proporzionale alla quantità di sostanza:
(2)
1
è
C = cm
dove C è detto calore specifico della sostanza, e m è la massa del campione.
Nel caso in cui i due corpi siano della stessa sostanza (e abbiano quindi lo stesso
calore specifico), la ?? diventa
Tf =
m1 T1 + m2 T2
m1 + m2
(3)
Analogia con i vasi comunicanti La formula ?? è analoga al risultato che si
ottiene per il livello del liquido che si ottiene collegando tra loro due recipienti
aperti (vasi comunicanti). Se i recipienti sono cilindrici e hanno superfici di
5
h1 h2 S1 hf S2 S1 S2 base rispettivamente S1 e S2 , il volume di liquido che essi contengono sarà
rispettivamente V1 = h1 S1 e V2 = h2 S2 , dove h1 e h2 è
Per trovare l’altezza di equilibro del liquido una volta che i recipienti sono
stati collegati, si impone la conservazione del volume del liquido totale:
S1 h1 + S2 h2 = S1hf + S2 hf
da cui
hf =
S1 h1 + S2 h2
S1 + S2
Nel caso dell’equilibrio termico, la temperatura è l’analogo dell’altezza del
liquido, e le capacità termiche l’analogo delle aree di base dei recipienti (proporzionali alle loro capacità se sono cilindrici). Anche questo caso dunque sembra
esserci qualcosa di conservato, analogo al volume di liquido.
In effetti dalla formula ?? si ricava facilmente che la quantità
∆Q1 = C1 (Tf − T1 )
che chiamiamo calore assorbito dal corpo 1 è uguale e opposta alla corrispondente quantità per il corpo 2
∆Q2 = C2 (Tf − T2 )
come se fosse la misura di volume di “fluido” uscito da uno dei due oggetti
e entrato nell’altro. Questa comportamento ha fatto sı̀ che per molti decenni il
calore fosse considerato a tutti gli effetti un fluido (il calorico).
Vedremo in seguito che la quantità conservata è in realtà l’energia, di cui
il calore rappresenta una forma. Tuttavia l’analogia continua a rimanere utile
(per aiutare l’intuito) nei casi in cui i corpi a contatto non si scambiano energia
meccanica.
1 A rigore la ?? è vera solo se le capacità termiche C e C sono costanti indipendenti
1
2
dalla temperatura, cosa che in certi casi non è verificata in maniera esatta. In quel caso la
formula rimane approssimativamente valida a patto che la variazioni delle capacità termiche
siano piccole per i cambiamenti di temperatura in gioco.
6
Unità di misura La relazione ∆Q = C∆T = cm∆T , una volta verificatane
sperimentalmente la validità per una grande classe di sostanze, si può usare per
misurare quantitativamente il calore scambiato. In particolare, storicamente si è
deciso di prendere come sostanza di riferimento l’acqua e definire la caloria come
la quantità di calore necessaria ad aumentare la temperatura di un grammo di
acqua da 14, 5◦ C a 15, 5◦ C. Il calore specifico dell’acqua a 14,5◦ C è quindi per
definizione 1 cal (◦ C g)−1 .
3.1
Equivalente meccanico della caloria
Il contatto termico tra corpi non è l’unico modo per aumentare la temperatura di
una sostanza: sappiamo dall’esperienza che quando in meccanica ci sono attriti
che rallentano il moto di corpi macroscopici dissipando energia meccanica, la
temperatura dei corpi coinvolti aumenta, tanto più quanto maggiore è l’energia
dissipata. Dove si perde energia meccanica “si crea” calore. L’ipotesi, suggestiva, che il calore creato non sia altro che l’energia persa andava naturalmente
verificata sperimentalmente, dimostrando che le due quantità (inizialmente non
imparentate, e misurate in unità diverse) sono in effetti proporzionali. Gli esperimenti storici che stabilirono questa proporzionalità si devono a James Joule il
quale trasferı̀ a una data quantità di acqua delle quantità misurabili di energia
meccanica (un modo può essere quello di fornire a un mulinello immerso nell’acqua un’energia cinetica nota, e poi lasciarlo fermare per attrito) misurando
quindi l’aumento di temperatura dell’acqua e deducendone (nota la capacità
termica dell’acqua) la quantità di calore assorbito. Naturalmente Joule non
misurava l’energia in joule, ma in termini moderni la proporzionalità da lui
misurata si esprime scrivendo che
1 cal ≈ 4.18 J
La proporzionalità permette di identificare le due grandezze: ciò che chiamavamo calore è una forma di energia, la cui conservazione – apparentemente
violata nella fisica dei corpi macroscopici in presenza di attriti meccanici – viene cosı̀ recuperata, inserendo nel bilancio anche gli scambi termici. È questo il
primo principio della termodinamca.
3.2
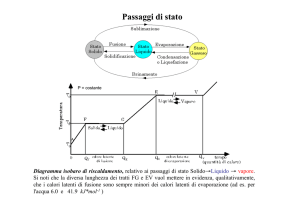
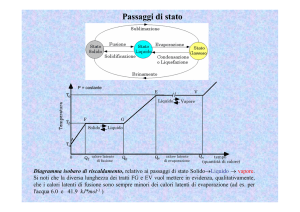
Passaggi di stato e calori latenti
Per una vasta classe di sostanze il passaggio di stato dallo stato solido a quello
liquido (fusione) o dallo stato liquido a quello gassoso (ebollizione) avviene a
una temperatura ben precisa e coinvolge il cosiddetto calore latente di fusione
o di ebollizione.
Nel caso della fusione, per esempio, accade che ricaldando una sostanza
allo stato solido la sua temperatura aumenta proporzionalmente al calore ceduto, secondo la formula Csolido ∆T = ∆Q. Quando la sostanza raggiunge una
temperatura critica (temperatura di fusione) si osserva che parte della sostanza
comincia a passare allo stato liquido: ogni ulteriore assorbimento di calore non
provoca alcun aumento della temperatura, che rimane uguale a quella di fusione, ma aumenta la percentuale di sostanza liquefatta, fino a quando tutta la
sostanza si trova allo stato liquido. A quel punto la temperatura riprende a salire proporzionalmente al calore assorbito, anche se in generale con una capacità
termica diversa: Cliquido ∆T = ∆Q.
7
Risulta che la quantità di calore necessaria alla fusione completa del campione di sostanza è proporzionale alla sua massa
∆Qfus = λfus m
Il fenomeno si presenta anche nel processo inverso di solidificazione: sottraendo calore al liquido questo abbassa la sua temperatura fino al raggiungimento
della temperatura di fusione (che dunque coincide con quella di solidificazione):
ulteriori sottrazioni di calore non fanno diminuire la temperatura ma aumentano la percentuale di sostanza passata allo stato solido, fino a quando il processo
non è completo. A quel punto la sostanza può ricominciare a raffreddarsi se
viene sottratto ulteriore calore.
Il fenomeno si spiega dal punto di vista microscopico con il fatto che il
passaggio di stato richiede energia per rompere i legami tra le molecole, e questa
energia è proporzionale al numero di molecole, dunque alla massa del campione
di sostanza. La stessa energia viene restituita quando il legame si riforma, nel
processo inverso.
La quantità λfus , caratteristica della sostanza, è quella che viene chiamata
calore latente di fusione, anche se ha in realtà le dimensioni di un calore per
unità di massa.
Evaporazione ed ebollizione Il caso del passaggio allo stato di vapore è
più complesso, perché anche a temperature più basse di quella di ebollizione
parte del liquido passa allo stato gassoso (evaporazione), fino a quando la parte
gassosa raggiunge una concentrazione di equilibrio, che per i gas rarefatti è
equivalente a una pressione (dato che a temperatura fissata p ∝ n/V ). La
pressione del vapore all’equilibrio con il liquido corrispondente è detta tensione
di vapore, ed è funzione della temperatura. Alla temperatura in cui la tensione
di vapore è uguale alla pressione atmosferica, diventa possibile la formazione
e l’espansione di bolle all’interno del liquido, perché la pressione del vapore
all’interno della bolla riesce a vincere quella del liquido circostante, e si ha il
fenomeno dell’ebollizione.
Il fenomeno del calore latente si verifica sia nell’evaporazione sia nell’ebollizione; il secondo caso, tuttavia, è molto più simile a quanto accade nella fusione,
perché una volta raggiunta l’ebollizione, ulteriori cessioni di calore al liquido non
ne aumentano la temperatura fino a quando tutto il liquido non è passato allo
stato gassoso. Anche il calore assorbito da un liquido in ebollizione per passare
completamente allo stato gassoso è proporzionale alla massa
∆Qeb = λeb m
• Esempio: ghiaccio in acqua
Un cubetto di ghiaccio di massa mg = 10 g alla temperatura Tg = −5◦ C
viene immerso in un litro d’acqua (ma = 100 g) inizialmente alla temperatura Ta = 20◦ C, in un recipiente termicamente isolato dall’esterno. Quale sarà la temperatura finale raggiunta dal sistema? (Calore specifico del
ghiaccio: cg = 0, 5cal/g, calore specifico dell’acqua liquida ca = 1, 0cal/g,
calore latente di fusione dell’acqua λ = 80cal/g)
8
Soluzione Supponiamo che il ghiaccio fonda completamente e che quindi la temperatura finale sia Tf > 0◦ C. Il calore assorbito dal ghiaccio nel
processo deve essere quello necessario a scendere alla temperatura di fusione Tfus = 0◦ C, più il calore necessario per fondere, più quello per salire
una volta fuso da Tfus a Tf
∆Qg = cg mg (Tfus − Tg ) + λmg + ca mg (Tf − Tfus )
Usando come prima la convenzione di considerare positivo il calore assorbito, abbiamo che il calore scambiato dall’acqua inizialmente liquida
sarà
∆Qa = Ca (Tf − Ta ) = ca ma (Tf − Ta )
La somma algebrica delle quantità di calore scambiato deve essere nulla:
cg mg (Tfus − Tg ) + λmg + ca mg (Tf − Tfus ) + ca ma (Tf − Ta ) = 0
da cui
Tf =
cg mg (Tg − Tfus ) − λmg + ca mg Tfus + ca ma Ta
cg mg + ca ma
Con i nostri dati iniziali troviamo Tf ≈ 13◦ C.
Approfondimento Notiamo che se nell’esempio visto avessimo avuto valori
diversi delle masse e temperature iniziali avremmo potuto trovare un valore
finale per la temperatura dell’acqua inferiore a 0◦ C, il che è assurdo. Questo
significa che la nostra ipotesi iniziale (il ghiaccio fonde tutto) sarebbe stata falsa.
A seconda dei casi, infatti, il risultato finale sarà una miscela di acqua e
ghiaccio a Tf = Tfus , o solo ghiaccio a Tfus < Tf < Tg
Più che scrivere in dettaglio tutti i casi e le relative formule risolutive, può
essere utile rappresentare graficamente il meccanismo:
Il grafico di figura ?? rappresenta la temperatura di un campione di sostanza
(per esempio acqua) in funzione del calore che assorbe. Nel primo tratto, in cui
la temperatura è inferiore a quella di fusione, il grafico è una retta di pendenza
∆T
1
∆Q = cs m , dove m è la massa del campione e cs il calore specifico della sostanza
allo stato solido. Quando la temperatura del solido raggiunge la temperatura
di fusione si ha il tratto orizzontale: ogni ulteriore ∆Q non fa aumentare la
temperatura ma rende possibile la fusione di una quantità di sostanza tale che
dQ = λf dm. Alla fine del tratto orizzontale, la cui lunghezza totale vale ∆Q =
mλf , tutto il campione è passato allo stato liquido e la temperatura ricomincia
∆T
= cl1m dove cl è il calore specifico dello
a salire, questa volta con pendenza ∆Q
stato liquido.
Un simile grafico, ma “ribaltato” descrive il comportamento di una sostanza
allo stato liquido a cui viene progressivamente sottratto calore. Anche in questo
caso la pendenza dei tratti obliqui e la lunghezza del tratto orizzontale dipendono dalla massa del campione. Se i due campioni sono a contatto, l’equilibrio
si raggiunge quando, a parità di calore scambiato, le due temperature si eguagliano, il che corrisponde al punto di intersezione dei due grafici. La figura ??
9
Tfus Ti ΔQ
Figura 2: Variazione della temperatura in funzione del calore assorbito per una
sostanza che attraversa un passaggio di stato.
Tf Tfus Tfus Tf Ti Ti ΔQ
ΔQ
Figura 3: Variazione della temperatura in funzione del calore scambiato per
due campioni diversi di sostanza inizialmente a temperatura diversa. La temperatura di equilibrio è quella in corrispondenza della quale i due grafici si
intersecano
illustra nel grafico di sinistra un caso simile a quello analizzato nell’esempio, in
cui all’equilibrio si ha solo liquido; nel grafico di destra invece, se la massa iniziale del liquido è suffcientemente bassa, l’equilibrio si raggiunge quando tutto
il liquido si è solidificato, e la temperatura finale è inferiore a quella di fusione.
10