ESERCIZI SVOLTI (raccolta di 62 esercizi in PDF).

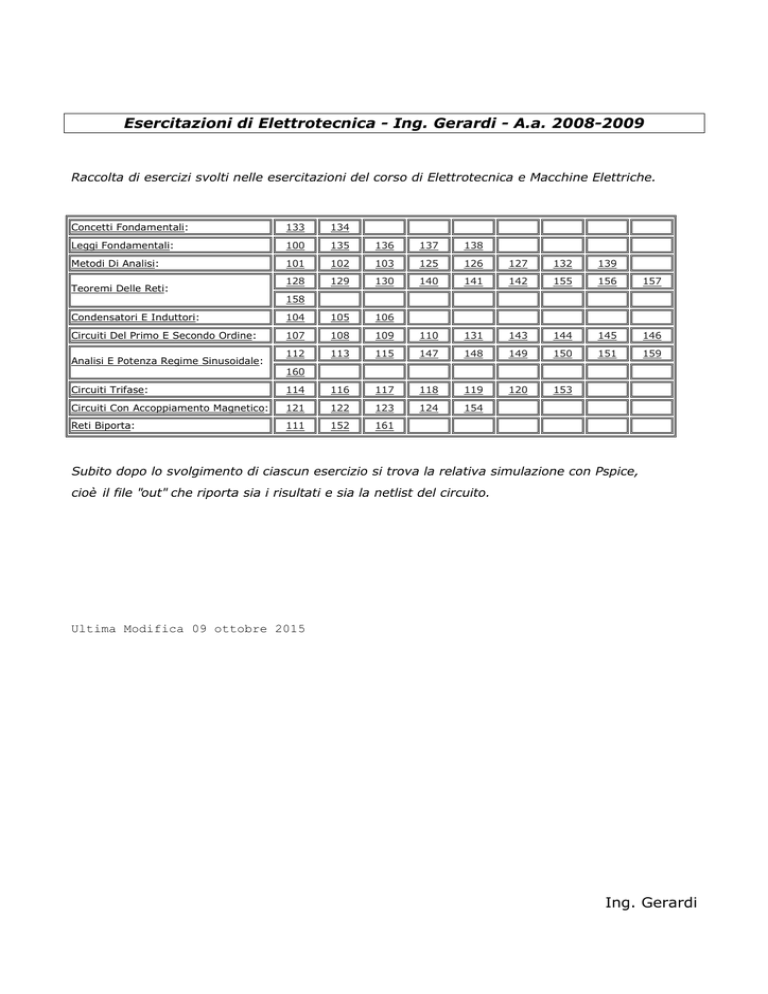
Esercitazioni di Elettrotecnica - Ing. Gerardi - A.a. 2008-2009
Raccolta di esercizi svolti nelle esercitazioni del corso di Elettrotecnica e Macchine Elettriche.
Concetti Fondamentali:
133
134
Leggi Fondamentali:
100
135
136
137
138
Metodi Di Analisi:
101
102
103
125
126
127
132
139
128
129
130
140
141
142
155
156
157
Teoremi Delle Reti:
158
Condensatori E Induttori:
104
105
106
Circuiti Del Primo E Secondo Ordine:
107
108
109
110
131
143
144
145
146
112
113
115
147
148
149
150
151
159
120
153
Analisi E Potenza Regime Sinusoidale:
160
Circuiti Trifase:
114
116
117
118
119
Circuiti Con Accoppiamento Magnetico:
121
122
123
124
154
Reti Biporta:
111
152
161
Subito dopo lo svolgimento di ciascun esercizio si trova la relativa simulazione con Pspice,
cioè
il file " out" che riporta sia i risultati e sia la netlist del circuito.
Ultima Modifica 09 ottobre 2015
Ing. Gerardi
ESERCIZIO 100
Calcolare tutte le correnti nei rami e verificare con il BILANCIO DELLE
POTENZE.
I1
E = 40 V
A
I3
R1
I2
+ E
−
R1 = 12 Ω
R3
R2
B
R2 = 10 Ω
I4
R4
I5
R5
R3 = 19 Ω
R4 = 30 Ω
R5 = 70 Ω
C
Soluzione:
Calcolo della resistenza equivalente “vista” dal generatore:
Req = R1 + {R2 //[R3 + R4 // R5 ]} = 20Ω
I1 =
E
= 2A
Req
V AC = E − R1 ⋅ I1 = 16V
I2 =
V AC
= 1,6 A
Req
I3 =
V AC
= 0,4 A
R3 + (R4 // R5 )
I4 =
VBC
= 0,28 A
R4
VBC = V AC − R3 ⋅ I 3 = 8,4V
I5 =
VBC
= 0,12 A
R5
Verifica del Bilancio delle potenze:
Pgen = E ⋅ I1 = −80W ;
PR1 = R1 ⋅ I12 = +48W ;
PR2 = R2 ⋅ I 22 = +25,6W
PR3 = R3 ⋅ I 32 = +3,04W ; PR4 = R4 ⋅ I 42 = +2,352W ; PR5 = R5 ⋅ I 52 = +1,008W
Per cui risulta vero che:
Pgeneratori + Putilizzatori = 0
Ing. Gerardi
**** 10/09/115 13:10:33 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 100
****
CIRCUIT DESCRIPTION
******************************************************************************
V_E 1 0 DC 40
R1 1 2 12
R2 2 0 10
R3 2 3 19
R4 3 0 30
R5 3 0 70
.DC V_E 40 40 1
.PRINT DC I(R1) I(R2) I(R3)
.PRINT DC I(R4) I(R5)
.END
**** 10/09/115 13:10:33 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 100
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V_E
I(R1)
I(R2)
I(R3)
4.000E+01 2.000E+00 1.600E+00 4.000E-01
**** 10/09/115 13:10:33 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 100
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V_E
I(R4)
I(R5)
4.000E+01 2.800E-01 1.200E-01
JOB CONCLUDED
TOTAL JOB TIME
.05
Ing. Gerardi
ESERCIZIO 101
Calcolare la tensione V0 per il circuito in figura.
A
+ 30V
−
I1
+ 20V
−
I3
+
4KΩ V0
−
I2
2KΩ
5KΩ
B
Soluzione:Metodo nodale
Si nota che V0 è uguale alla tensione nodale EA con il nodo B di riferimento.
V0
=0
4
1) KCL nodo A
− I1 − I 2 +
2) Vincolo al generatore da 30V
I1 =
30 − E A
2
3) Vincolo al generatore da 20V
I2 =
20 − E A
5
Sostituendo la (2) e la (3) nella (1) si ottiene:
V0 − 30 V0 − 20 V0
+
+
=0
2
5
4
I1 =
30 − E A
= 5 mA = I3
2
380
= 20V = EA
19
I2 =
20 − E A
= 0A
5
V0 =
Verifica del Bilancio delle potenze:
P30 V = E ⋅ I1 = −150 mW ; P20 V = E ⋅ I2 = 0 W
P2KΩ = R ⋅ I 12 = 50 mW ; P5KΩ = R ⋅ I 22 = 0 W ; P2KΩ = R ⋅ I 12 = 150 mW
Per cui risulta vero che:
Pgeneratori + Putilizzatori = 0
Ing. Gerardi
**** 10/09/115 13:44:04 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 101
****
CIRCUIT DESCRIPTION
******************************************************************************
V1 1 2 DC 30
R1 0 2 2E+03
V2 1 3 DC 20
R2 0 3 5E+03
R3 1 0 4E+03
.DC V1 30 30 1
.PRINT DC V(1) I(R1) I(R2) I(R3)
.END
**** 10/09/115 13:44:04 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 101
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V1
V(1)
I(R1)
I(R2)
I(R3)
3.000E+01 2.000E+01 5.000E-03 0.000E+00 5.000E-03
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 102
Calcolare le tensioni nodali V1 e V2 per il circuito in figura.
2Ω
V1
V2
+−
I1
I2
2V
8Ω
4Ω
3A
Soluzione:Metodo agli anelli
Nel circuito ci sono 2 correnti di anello IA (maglia SX), e IB 1(maglia DX).
V1
8Ω
V2
+−
2Ω
2V
IA
4Ω
IB
3A
Si nota subito che I B = 3 A , si scrive la KVL alla maglia a SX (antiorario):
(8 + 4 + 2) ⋅ I A − 2 − 4 ⋅ I B
=0
I A = 1A
Dalle correnti di maglia si ricavano le tensioni nodali richieste:
V1 = 8 ⋅ I A = 8V

V2 = 4 ⋅ (I B − I A ) = 8V
Verifica del Bilancio delle potenze:
Pgen.3 A = V2 ⋅ 3 = −24W ;
P8Ω = 8 ⋅ I 82Ω = +8W ;
Per cui risulta vero che:
Pgen.2V = 2 ⋅ I A = −2W
P4Ω = 8 ⋅ I 42Ω = +16W ;
P2Ω = 8 ⋅ I 22Ω = +2W
Pgeneratori + Putilizzatori = 0
Ing. Gerardi
**** 10/09/115 13:52:44 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 102
****
CIRCUIT DESCRIPTION
******************************************************************************
R1 1 0 8
R2 3 1 2
V0 3 2 DC 2
R3 2 0 4
I0 0 2 DC 3
.DC V0 2 2 1
.PRINT DC V(1) V(2) I(R2) I(R3)
.END
**** 10/09/115 13:52:44 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 102
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V0
V(1)
V(2)
I(R2)
I(R3)
2.000E+00 8.000E+00 8.000E+00 1.000E+00 2.000E+00
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 103
Calcolare le tensioni nodali EA e EB per il circuito in figura.
A Iy
−+
B
8V
5A
10Ω
IA
5Ω 2A
IB
IC
Soluzione:Metodo della sovrapposizione degli effetti
1
1
Nel circuito vi sono 3 generatori indipendenti,
per cui si calcolano
3 effetti.
A
A
B
A
B
B
−+
8V
5A
10Ω
10Ω
5Ω
5Ω 2A
10Ω
5Ω
I
1° Effetto
2° Effetto
3° Effetto
1^effetto, agisce solo il generatore da 5A: applicando il partitore di corrente
I10Ω = 5 ⋅
5
5
= A
(10 + 5) 3
E AI = E BI = 10 ⋅ I10Ω =
50
V
3
2^effetto, agisce solo il generatore da 2A: applicando il partitore di corrente
I 5Ω = 2 ⋅
10
4
= A
(10 + 5) 3
E AII = E BII = 5 ⋅ I 5Ω =
20
V
3
3^effetto, agisce solo il generatore da 8V:
I=
8
8
= A
(10 + 5) 15
8
E BIII = 5 ⋅ I = V
3
E AIII = −10 ⋅ I = −
16
V
3
Sommando i due effetti si ha:
E A = E AI + E AII + E AIII = +18V
E B = E BI + E BII + E BIII = +26V
Ing. Gerardi
1
**** 10/09/115 13:57:47 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 103
****
CIRCUIT DESCRIPTION
******************************************************************************
I1 0 1 DC 5
R2 1 0 10
V3 2 1 DC 8
R4 2 0 5
I5 0 2 DC 2
.DC V3 8 8 1
*le tensioni EA e EB sono rispettivamente V(1) e V(2)
.PRINT DC V(1) V(2) I(R2) I(R4)
.END
**** 10/09/115 13:57:47 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 103
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V3
V(1)
V(2)
I(R2)
I(R4)
8.000E+00 1.800E+01 2.600E+01 1.800E+00 5.200E+00
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 104
Calcolare le tensioni sui condensatori e le correnti negli induttori in
condizioni stazionarie per il circuito in figura.
L1
4Ω
C1
+ 30V
−
6Ω
C2
L2
Soluzione:
In condizioni di regime stazionario condensatore e induttore si comportano
1
come un circuito aperto ed un cortocircuito. Il circuito si trasforma:
iL1
4Ω
+
6Ω
vC1
+ 30V
−
−
+
vC2
iL2
−
VC 2 = 0V
perché c’è il cortocircuito.
I L1 = I L2 =
VC1 = 30 ⋅
30
= 3A
(6 + 4)
6
= 18V
(6 + 4)
(partitore di corrente)
(partitore di tensione)
Ing. Gerardi
**** 10/09/115 14:07:09 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 104
****
CIRCUIT DESCRIPTION
******************************************************************************
V 1 0 DC 30
R1 1 2 4
*si inseriscono valori a piacere per condensatori e induttori
*essendo prevista l'analisi in regime stazionario
C1 2 0 10e-3
L1 2 4 20e-3
R2 4 5 6
C2 5 0 30E-3
L2 5 0 40E-3
.DC V 30 30 1
.PRINT DC V(C1) V(C2) I(L1) I(L2)
.END
**** 10/09/115 14:07:09 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 104
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V
V(C1)
V(C2)
I(L1)
I(L2)
3.000E+01 1.800E+01 0.000E+00 3.000E+00 3.000E+00
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 105
Calcolare l’energia immagazzinata dai condensatori in condizioni stazionarie
per il circuito in figura.
3kΩ
20mF
1kΩ
+ 10V
−
C2
C1
10mF
6kΩ
Soluzione:
In condizioni di regime stazionario i due condensatori sono carichi per cui si
1
comportano come circuiti aperti. Il circuito si trasforma:
3kΩ
1kΩ
+ 10V
−
+ vC2 −
+
vC1
6kΩ
−
Le resistenze espresse in kΩ.Applicando ripetutamente il partitore si ha:
VC1 = 10 ⋅
(3 + 6) = 9V
1 + (3 + 6 )
Oppure si calcola:
VC 2 = VC1 ⋅
VC 2 = 10 ⋅
3
= 3V
6+3
3
= 3V
3 + (1 + 6 )
Le energie immagazzinate dai due condensatori sono:
WC1 =
1
⋅ C1 ⋅ VC21 = 405mJ
2
WC2 =
1
⋅ C2 ⋅ VC22 = 90mJ
2
Ing. Gerardi
**** 10/09/115 14:11:24 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 105
****
CIRCUIT DESCRIPTION
******************************************************************************
V 1 0 DC 10
R1 1 2 1E3
*si inseriscono valori a piacere per condensatori e induttori
* essendo prevista l'analisi in regime stazionario
C1 2 0 10e-3
R2 2 3 3E3
C2 2 3 20E-3
R3 3 0 6E3
.DC V 10 10 1
.PRINT DC V(C1) V(C2)
.END
**** 10/09/115 14:11:24 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 105
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V
V(C1)
V(C2)
1.000E+01 9.000E+00 3.000E+00
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 106
Determinare il valore della resistenza R in modo che a regime, l’energia
immagazzinata dal condensatore si uguale a quella dall’induttore.
R
160mF
C
5A
2Ω
4mH
L
Soluzione:
In condizioni di regime stazionario condensatore e induttore si comportano
1
come un circuito aperto ed un cortocircuito.
Il circuito si trasforma:
iR
iL = iR = 5 ⋅
R
+ vC −
5A
2Ω
2
10
=
2+R 2+R
vC = R ⋅ iL =
iL
10 ⋅ R
2+R
Uguagliando le energie immagazzinate da C e L, si determina il valore di R:
1
1
⋅ C ⋅ vC2 = ⋅ L ⋅ iL2
2
2
WC = WL
−6
−3
R=±
4 ⋅ 10 − 3
= +5Ω
160 ⋅ 10 − 6
Avendo scartato il valore negativo. L’energia immagazzinata vale:
160 ⋅ 10
⋅ R = 4 ⋅ 10
2
WC = WL = 4,082mJ
iL = iR = 5 ⋅
2
10
=
= 1,429 A
2+R 2+R
vC = R ⋅ iL =
10 ⋅ R
= 7,143 V
2+R
Ing. Gerardi
**** 10/09/115 15:06:12 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 106
****
CIRCUIT DESCRIPTION
******************************************************************************
I 0 1 DC 5
R1 1 0 2
*si inseriscono valori a piacere per condensatori e induttori
* essendo prevista l'analisi in regime stazionario
C 1 2 10e-3
*si inserisce una resistenza di 5 ohm verificando i
*valori di v_C e i_L
R125
L 2 0 20E-3
.DC I 5 5 1
.PRINT DC V(C) V(R) I(L) I(R)
.END
**** 10/09/115 15:06:12 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 106
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
I
V(C)
V(R)
I(L)
I(R)
5.000E+00 7.143E+00 7.143E+00 1.429E+00 1.429E+00
JOB CONCLUDED
TOTAL JOB TIME
.05
Ing. Gerardi
ESERCIZIO 107
Calcolare la corrente i0(t) per t < 0 e per t ≥ 0.
1
t=0
40Ω
i0
0.5 · i0
3F
80Ω
+ 80V
−
Soluzione:
I
1) t < 0 Il valore per t<0 è vCI
= 0 , perché è inizialmente scarico.
I
1
si considera
il condensatore carico:
Per calcolare il valore finale vCF
Si applica il metodo nodale:
i0
+
I
80Ω vCF
−
40Ω
0.5 · i0
+ 80V
−
I
I
 vCF
− 80
vCF

+
− 0,5 ⋅
 80
40

I
vCF
=
I
 vCF
+
=0
 80

320
= 64V
5
Per calcolare la costante di tempo si ricava R1 TH con Thevenin:
A
Si determina V0 col nodale:
i0
40Ω
+
0.5 · i0
1A
V0
80Ω
+
0
V 
V
− 0,5 ⋅  0  − 1 + 0 = 0
 80 
80
 
V
40
−
V0 =
80
I
= 32V = RTH
= 32Ω
2,5
I
⋅ C = 32 ⋅ 3 = 96 sec .Per t < 0 vC e i0 variano con le seguenti leggi:
τ I = RTH
vCI
(t )
I
= vCF
+
(
I
vCI
I
− vCF
)⋅ e
− t
τI
= 64 − 64 ⋅ e
−t
96
V
Ing. Gerardi
i0I
−t
vCI (t )
(t ) =
= 0,8 − 0,8 ⋅ e 96 A
80
( )
II
I
2) t > 0 Il valore iniziale per t ≥ 0 è: vCI
= vC 0 − = vCF
= 64V
II
Il circuito è autonomo, vCF
= 0 . Per la costante di tempo si ricava RTH:
A
Si determina V0 col nodale:
V 
V
− 0,5 ⋅  0  − 1 + 0 = 0
 80 
80
 
i0
+
1A
V0
80Ω
−
0.5 · i0
II
= 160Ω
V0 = 160V = RTH
II
⋅ C =160⋅ 3 = 480 sec
τ II = RTH
La costante di tempo vale:
Quindi per t ≥ 0 la tensione vC e la corrente i0 variano con le seguenti leggi:
(
)⋅ e
− t
vCII
(t )
i0II
−t
vCII (t )
= 0,8 ⋅ e 480 A
(t ) =
80
II
= vCF
+
II
vCI
II
− vCF
τ II
= 64 ⋅ e
−t
480V
Ing. Gerardi
ESERCIZIO 108
Calcolare la corrente i0(t) per t < 0 e per t ≥ 0.
a
b
t=0
+ 30V
−
3Ω
12V +
−
6Ω
2F
i
Soluzione:
( )
1) t < 0: posizione “a” Per il valore iniziale vC 0 − il condensatore è carico:
6Ω
+ 30V
−
( )
vCI = vC 0 − = 30 ⋅
+
3Ω vCI
−
3
= +10V
6+3
2) t > 0: posizione “b” Per il valore finale il condensatore è aperto:
vCF = 12 ⋅
3
= +4V
6+3
La costante di tempo si ricava RTH passivizzando il generatore da 12V:
RTH =
6⋅3
= 2Ω
6+3
τ = RTH ⋅ C = 4 sec
Quindi per t ≥ 0 la tensione vC e la corrente i variano con le seguenti leggi:
(
)
vC (t ) = vCF + vCI − vCF ⋅ e
i0 (t ) = C ⋅
− t
τ
= 4 + 6⋅e
−t
4V
dvC (t )
−t
 1 −t
= 2 ⋅ 6 ⋅  −  ⋅ e 4 = −3 ⋅ e 4 A
dt
 4
Ing. Gerardi
ESERCIZIO 109
L’interruttore S è rimasto nella posizione “A” per molto tempo. Nell’istante
t=0 si sposta nella posizione “B”. Infine si sposta in posizione “C” dopo
0,25s. Calcolare la corrente iL(t) per t →-∞ a t →+∞.
10Ω
iL
+
1H
vL
10Ω
30Ω
A
−
S
+−
B
10V
+−
1Ω
+−
30V
C
10V
Soluzione:
1) t < 0: posizione “A” Per t<0 l’interruttore è in posizione “A”:
1H
i L A (− ∞ ) = i LI A = 0 A
10Ω
iL
+
vL
10
1
=− A
10 + 10
2
perché L è in cortocircuito.
i L A (+ ∞ ) = i LFA = −
10Ω
−
+−
10V
La costante di tempo si calcola dalla resistenza equivalente di Thevenin:
τA =
RTH A = 10 + 10 = 20Ω
(
)
iL (t ) = iLF + iLI − iLF ⋅ e
A
A
A
A
− t
τA
1 1
= − + ⋅ e − 20⋅t A
2 2
L
RTH
=
1
= 50m sec
20
A
t<0
( )
2) 0 ≤ t < 0,25sec: posizione “B” La C.I. è: i L B 0 − = i L A (∞ ) = i LI B = −0,5 A
A regime si avrebbe:
i LB (+ ∞ ) = iLFB = −
10 + 30
= −1 A
10 + 30
Ing. Gerardi
1H
RTH B = 10 + 30 = 40Ω
10Ω
iL
+
vL
30Ω
τB =
−
+−
+−
10V
30V
(
)
i L (t ) = i LF + i LI − i LF ⋅ e
B
B
B
B
− t
τB
= −1 +
L
RTH
=
1
= 25m sec
40
B
1 − 40⋅t
⋅e
A
2
0≤t<0,25s
3)“S” commuta in posizione “C” La condizione di regime in posizione “B”
viene raggiunta dopo 5τ=125ms; la commutazione nella posizione “C”
avviene dopo 125ms, quindi la C.I. vale:
iL 1H
+ vL −
1Ω
τC =
L
RTH
+−
10V
i LC (+ ∞ ) = iLFC =
+−
10V
RTH C = 1Ω
10 − 10
= 0A
1
= 1sec
C
(
)
iL (t ) = iLF + iLI − iLF ⋅ e
C
( )
i LC 0 − = iL B (∞ ) = i LI C = −1A
C
C
C
− (t − 0.25)
τC
= −e − (t − 0.25) A
t ≥ 0,25s
Ing. Gerardi
ESERCIZIO 110
L’interruttore è chiuso da molto tempo, e si apre in t = 0. Determinare la
tensione v(t) per t ≥ 0.
[N.B. u(t) è la funzione gradino unitario]
t=0
3A
1H
+
v
−
10Ω
4F
5Ω
4 · u(t)A
Soluzione:
1) t < 0 Si calcolano le due C.I. prima dell’apertura del tasto.Il circuito è:
3A
vC (0− )
10Ω
( ) 1010+ 5 = 2 A
vC (0 − ) = 5 ⋅ iL (0 − ) = 10V
iL 0 − = 3 ⋅
iL
+
5Ω
−
2) t ≥ 0 Il circuito cambia e applicando le KCL e KVL, si ha:
iL 1H
+ vL −
+
vC
−
iC
+
4F
iL = −iC

iR − iL − 4 = 0
− v + v + v = 0
L
R
 C
iR
vR 5Ω
−
 vR
+ 5 − iL − 4 = 0

− vC + L ⋅ diL + vR = 0

dt
4A
dvC
 vR
+
+
4
⋅
−4=0
 5
dt

2
+ v + 4 ⋅ d vC = v
R
 C
dt 2
dv
vC 4 d 2vC
+
+ ⋅ 2 + 4 ⋅ C − 4 = 0 (Equ.differenziale del 2° ord.non omogenea
5 5 dt
dt
4⋅
d 2vC
dt 2
+ 20 ⋅
dvC
+ vC = 20
dt
(*)
Ing. Gerardi
L’ equazione caratteristica associata, serve per calcolare i 2 valori di λ:
4 ⋅ λ2 + 20 ⋅ λ + 1 = 0
λ1 =
(**)
2
− 0,051
− 4,949
Le due soluzioni sono reali, distinte e negative, (risposta sovrasmorzata):
vC (t ) = K1 ⋅ eλ1 ⋅t + K 2 ⋅ e λ2 ⋅t + vC P (t )
(***)
Sostituendo la (***) nella (*), si ottiene:
vC P (t ) = cos t . = 20V
Calcolo di K1 e K2: (C.I. vC(0)=10V, iL(0)=2A):
vC (0 ) = K1 ⋅ e λ⋅0 + K 2 ⋅ e λ ⋅0 + 20 = 10V
iL (0 ) = −iC (0 ) = − C ⋅
d vC
dt
t =0
=−
K 1 + K 2 + 20 = 10
1
= (K1 ⋅ λ 1 ) + (K 2 ⋅ λ 2 )
2
Risolvendo si determinano le due costanti:
 K1 = −9 ,795

 K 2 = −0 ,205
Sostituendo nella (***):
vC (t ) = −9 ,795 ⋅ e −0 ,051⋅t − 0 ,205 ⋅ t ⋅ e − 4 ,949 ⋅t + 20V
Ing. Gerardi
ESERCIZIO 111
Calcolare la potenza assorbita dal Doppio Bipolo nel circuito in figura.
+
10A
V1
I1
I2
1Ω
1Ω
1Ω
2Ω
V2
1Ω
−
+
10A
−
Soluzione: (si risolve mediante i parametri “Y”)
I parametri Y di un doppio bipolo si ricavano dalle relazioni seguenti:
 I1 = Y11 ⋅V1 + Y12 ⋅ V2
[Si userà il metodo agli nodale per il calcolo di tutti i parametri.]

I
=
Y
⋅
V
+
Y
⋅
V
 2
21 1
22 2
- Calcolo Y11 e Y21:Si mette in porta 1 un gen. I1=1A, (porta 2 cortocircuitata).
I1
A
B
1Ω
I2
I2
+
1A
V1
−
1Ω
2Ω
1Ω
V2 = 0
1Ω
B
1) KCL nodo A
− 1 + E A + 0,5 ⋅ ( E A − E B ) + ( E A − E B ) = 0
2) KCL nodo B
+ ( EB − E A ) + 0,5 ⋅ ( EB − E A ) + E B = 0
5 
5

E
=
V
V
=
E
=
V
A
1
A

8
2
I
I
8 ; 
8
; Y11 = 1
= S ; Y21 = 2
=− S


5
V1 V = 0 5
V1 V = 0
 EB = 3 V  I = EB − E A = − 1 A
2
2
2

8 
1
4
- Calcolo Y12 e Y22: Si mette in porta 2 un gen. I2=1A, (porta 1 cortocircuitata).
1) KCL nodo C
− 1 + EC + ( EC − EA ) = 0
2) KCL nodo B
+ ( EA − EC ) + 0,5 ⋅ (E A ) + E A = 0
Ing. Gerardi
I1
A
C
I2
1Ω
+
V1 = 0
1Ω
1Ω
2Ω
V2
1A
−
1Ω
A
I1
Da cui si ha: (sarà Y12 = Y21, il doppio bipolo è reciproco, e si usa la “rete a π“)
EA
1 
1

E
=
V
I
=
−
=
−
A
A
1

I1
I2
2
8
4 ; 
1
4 ;
;
Y
Y
=
=
−
S
=
=
S


12
22
5
5
V
V
5
5
2 V1 = 0
2 V1 = 0
 EC = V V2 = EC = V


8 
8
I2
+
10A
I1
5
Ω
6
V1
5
Ω
2
5
Ω
6
+
I3
10A
V2
−
−
Si calcolano le correnti I1,I2 e I3, applicando 1la sovrapposizione degli effetti
I2I
10A
5
Ω
6
I1I
I2II
5
Ω
2
5
Ω
6
I1II
I3I
5
Ω
6
1^ Effetto: agisce il generatore a sinistra.
I1I = 10 ⋅
(5 2 + 5 6) = 15 A ;
(5 2 + 5 6) + 5 6 2
I 2I = I 3I = 10 ⋅
5
I 2II = − I1II = − A ;
2
I1 = 10 A ;
I2 = 0 A;
Sommando gli effetti:
V1 = 8,333 V ;
La potenza assorbita vale:
I3II
10A
2^ Effetto: agisce il generatore a destra.
5
A;
2
Sommando gli effetti:
I1II =
5
Ω
2
5
Ω
6
56
5
= A
(5 2 + 5 6) + 5 6 2
I 3II =
I 3 = 10 A
15
A
2
V2 = 8,333 V
5
 5
 5
 500
P =  ⋅ I12  +  ⋅ I 22  +  ⋅ I 32  =
W
3
6
 2
 6

Ing. Gerardi
**** 10/09/115 19:16:36 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 111
****
CIRCUIT DESCRIPTION
******************************************************************************
I1 0 1 DC 10
R1 1 0 1
R2 1 2 1
R3 2 3 1
I4 3 2 DC 10
R5 3 0 1
R6 1 3 2
.DC I1 10 10 1
.PRINT DC V(R1) V(R3)
.END
**** 10/09/115 19:16:36 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 111
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
I1
V(R1)
V(R3)
1.000E+01 8.333E+00 8.333E+00
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 112
Calcolare la potenza assorbita dal circuito in figura e verificare il bilancio
della potenza complessa.
2
3F
1
6H
L
C
i0 (t)
+ v (t)
− 1
1Ω
1Ω
R2
v1 (t) = 30 · cos(3 · t)
i0 (t) = 40 · cos(3 · t)
R1
Soluzione: Si risolve il circuito trasformato coi “fasori” col metodo “nodale”:
1
A
I1 +j 2 Ω
1
I2 −j 2 Ω
+
+
40 0A
+ 30 0V
−
I0
v0
−
1Ω
E A − 30
EA
− 40 +
=0
1
1
+j
1− j
2
2
EA =
1Ω
I1 =
30 − E A
= −10 + j 20 = 22.361∠116.565 A
+ j 0,5
I2 =
EA
= 30 + j 20 = 36.056∠33.690 A
1 − j 0,5
La potenza attiva e reattiva totali sono:
[( ) ( )]
40 − j 60
= 40 + j 5V
0.8 − j1.6
[(
) (
)]
PT = 0,5 ⋅ 1 ⋅ I 02 + 1 ⋅ I 22 = 1450W QT = 0,5 ⋅ 0,5 ⋅ I 02 − 0,5 ⋅ I 22 = −200VAR
Verifica con le potenze complesse:
(
)
(
)
1
1
ST = S gen _ V1 + S gen _ I 0 = ⋅ V1 ⋅ I1* + ⋅ V0 ⋅ I 0* = 1450 − j 200VA
2
2
V0 è la tensione sul generatore di corrente:
V0 = E A + 1 ⋅ I 0 = 80 + j5V
Ing. Gerardi
**** 10/10/115 13:40:46 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 112
****
CIRCUIT DESCRIPTION
******************************************************************************
V1 1 0 AC 30 0
L 1 2 166.667E-3
I0 3 2 AC 40 0
R1 3 0 1
C 2 4 666.667E-3
R2 4 0 1
*la tensione E_A V(2)
*la corrente I1 I(L)
*la corrente I2 I(C)
.AC LIN 1 .47746 .47746
.PRINT AC VR(2) VI(2) IR(L) II(L)
.PRINT AC IR(C) II(C)
.END
**** 10/10/115 13:40:46 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 112
****
SMALL SIGNAL BIAS SOLUTION
TEMPERATURE = 27.000 DEG C
**** 10/10/115 13:40:46 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 112
**** AC ANALYSIS
TEMPERATURE = 27.000 DEG C
******************************************************************************
FREQ
VR(2)
VI(2)
IR(L)
II(L)
4.775E-01 4.000E+01 5.000E+00 -1.000E+01 2.000E+01
******************************************************************************
FREQ
IR(C)
II(C)
4.775E-01 3.000E+01 2.000E+01
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 113
Del circuito in figura sono noti (valori di tensione e corrente efficaci):
ω = 1 rad/s; BIPOLO “X” [PX=0; QX=1kVAR induttivi]
Calcolare V1, I1, cos ϕ1 e verificare il bilancio della potenza complessa.
I1
1
5Ω
V1
cosϕ1
X
1F
+ 10A
100V
−
75mF
Soluzione: Si risolve il circuito trasformato coi “fasori” con “Boucherot”:
DI
CI
ID
BI
IC
AI
IB
1
5Ω
S = P2 + Q2
X
V1
1Ω
10Ω
cosϕ1
D
C
B
PA − A' = 100 ⋅ 10 = 1000 W
S A − A'
V A − A'
= 12,5 A
PC − C ' = PB − B '
40
3 Ω
A
;
PB − B ' = PA − A' + PX = 1 kW ;
IA =
Si ricorda che
IA
;
;
Q A − A'
100 2
=−
= −750 VAR
40 3
QB − B ' = Q A − A' + Q X = +250 VAR
VB − B ' =
S B − B'
V B − B'
QC − C ' = QB − B '
= 82,46V
VC2− C '
−
= −6,55kVAR
XC
QD − D ' = QC − C '
1
;
PD − D ' = PC − C ' + ⋅ I D2 = 2,29kW
5
S
S
V1 = D − D ' = 86,361V
I C = I D = I 1 = C − C ' = 80,35 A ;
ID
VC − C '
P
ϕ1 = −70,72°
cos ϕ1 = D − D ' = 0,3302(capacitivo) ;
S D − D'
Ing. Gerardi
**** 10/10/115 16:59:45 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 113
****
CIRCUIT DESCRIPTION
******************************************************************************
*f = w/(2*pi) = 0.15915 Hz
V1 1 0 AC 86.361 -70.72
R1 1 2 .2
C1 2 0 1
*il bipolo X solo induttivo per cui
*si calcola LX=(QX/IA^2)/w = 6.4 ohm
LX 2 3 6.4
*la resistenza R2=100V/10A= 10 ohm
R2 3 0 10
C2 3 0 75E-3
*la tensione VA-A' V(3)
*la corrente IX=IA=IB I(LX)
*la tensione VB-B' V(2)
*la corrente IC=I1 I(R1)
*si calcolano solo i moduli
.AC LIN 1 0.15915 0.15915
.PRINT AC V(3) I(LX) V(2) I(R1)
.END
**** 10/10/115 16:59:45 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 113
****
SMALL SIGNAL BIAS SOLUTION
****
AC ANALYSIS
TEMPERATURE = 27.000 DEG C
TEMPERATURE = 27.000 DEG C
******************************************************************************
FREQ
V(3)
I(LX)
V(2)
I(R1)
1.592E-01 1.000E+02 1.250E+01 8.246E+01 8.035E+01
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 114
Una tensione V = 325 ∠0°V, f = 50Hz, alimenta 3 carichi in parallelo:
a) carico ohmico-induttivo serie R1 = 6 Ω, L1 = 25,46 mH;
b) carico ohmico R2 = 25 Ω;
c) carico ohmico-induttivo serie R3 = 39 Ω, L3 = 165,521 mH;
Calcolare la corrente totale assorbita dai 3 carichi ed il fattore di potenza;
calcolare il valore del condensatore per rifasare ad un fattore di potenza pari a
0,9, e calcolare la corrente a monte del condensatore dopo il rifasamento.
Soluzione: Si risolve il circuito trasformato coi “fasori” con “Boucherot”:
V
IT
I1
6Ω
I3
I2
R1
25Ω
8Ω
39Ω
R3
52Ω
X3
R2
X1
−
−
−
Z1 = 6 + j8 = 10∠53,130Ω ;
Z 2 = 25Ω ;
Z 3 = 39 + j 52 = 65∠53,130Ω
−
−
−
− V
− V
− V
I1 = − = 32,5∠ − 53,13 A ;
I 2 = − = 13∠0 A ;
I 3 = − = 5∠ − 53,13 A
Z1
Z2
Z3
−
−
IT = ∑ I = (19,5 − j 26) + (13) + (3 − j 4) = 35,5 − j 30 = 46,478∠ − 40,2 A
− 1 − −
ST = ⋅ V ⋅ IT* = 5768,25 + j 4875 = 7552,373∠40,203VA ; cosϕT = 0.7638
2
*****************************************************************************
Si rifasa a cos ϕT' = 0,9 :
C=
2 ⋅ QC
ω ⋅V 2
= 125,458µF
(
)
QC = PT ⋅ tgϕT − tgϕT' = 2081,556VAR
IT' =
2 ⋅ PT
V ⋅ cos ϕT'
= 39,441A
Ing. Gerardi
**** 10/10/115 17:57:32 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 114
******************************************************************************
*w = 2*pi*f = 314.16 rad/s
V1 1 0 AC 325 0
*per le correnti IT e IT' si inseriscono due generatori
*di 0V che funzionano da amperometri, per cui si ha
*IT'=I(Vamp1) e IT=I(Vamp2)
Vamp1 1 2 AC 0 0
Vamp2 2 3 AC 0 0
R1 3 4 6
*si inseriscono una resistenza elevatissima in parallelo
*agli induttori per evitare il messaggio di errore di PSPICE
L1 4 0 25.46E-3
Rinf1 2 0 1E12
R2 3 0 25
R3 3 5 39
L3 5 0 165.521E-3
Rinf2 4 0 1E12
*si inserice il condensatore di rifasamento Crif
Crif 2 0 125.458E-6
*la corrente I1 I(R1)
*la corrente I2 I(R2)
*la corrente I3 I(R3)
.AC LIN 1 50 50
.PRINT AC I(R1) IP(R1) I(R2) IP(R2)
.PRINT AC I(R3) IP(R3) I(Vamp1) IP(Vamp1)
.PRINT AC I(Vamp2) IP(Vamp2)
.END
**** 10/10/115 17:57:32 ******* Evaluation PSpice (September 1991) ***********
FREQ
I(R1)
IP(R1)
I(R2)
IP(R2)
5.000E+01 3.250E+01 -5.312E+01 1.300E+01 0.000E+00
******************************************************************************
FREQ
I(R3)
IP(R3)
I(Vamp1) IP(Vamp1)
5.000E+01 5.000E+00 -5.313E+01 3.945E+01 -2.584E+01
******************************************************************************
FREQ
I(Vamp2) IP(Vamp2)
5.000E+01 4.648E+01 -4.020E+01
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 115
Quattro carichi ohmico-induttivi sono collegati in parallelo e vengono
alimentati da una tensione V = 230 ∠0°V (efficaci), f = 50Hz:
a) P1 = 1 kW ;
Q1 = + 3 kVAR;
b) S2 = 2 kVA ;
cosϕ2 = 1;
c) P3 = 1,5 kW ;
tgϕ3 = 1;
d) S4 = 4 kVA ;
cosϕ4 = 0,5
Calcolare la corrente totale assorbita dai 3 carichi ed il fattore di potenza;
calcolare il valore del condensatore per rifasare ad un fattore di potenza pari a
0,9, e calcolare la corrente a monte del condensatore dopo il rifasamento.
Soluzione: Si risolve il circuito con “Boucherot”:
V
IT
C
Carico
1
Carico
2
Carico
3
Carico
4
PT = ∑ P = 1 + 2 + 1,5 + 2 = 6,5kW
QT = ∑ Q = 3 + 1,5 + 3,46 = 7,96kVAR
tgϕT =
QT
= 1,2252
PT
Si rifasa a cos ϕT' = 0,9 :
C=
QC
ω ⋅V 2
≅ 290 µF
cos ϕT = 0,6323
(
IT =
PT
V ⋅ cos ϕT
= 44,695 A
)
QC = PT ⋅ tgϕT − tgϕT' ≅ 4816VAR
IT' =
PT
V ⋅ cos ϕT'
= 31,4 A
Ing. Gerardi
ESERCIZIO 116
Calcolare le correnti di linea totali nel circuito di figura (V = 380 V efficaci).
1
I1
R1
30Ω
40Ω
30Ω
2
3
30Ω
I3
40Ω
I1T
X2
R1
30Ω
Si pone la fase delle tensioni di linea:
−
V12 = 380∠120V
−
V23 = 380∠0V
V− = 380∠ − 120V
 31
R2
I2
40Ω
I1S X1
I2S X1
40Ω
O
R2
I2T
X2
R1
30Ω
−
 E1 = 219,393∠90V
−
 E2 = 219,393∠ − 30V
 E− = 219,393∠ − 150V
 3
I3S X1
40Ω
Soluzione:
−
E1 219,393∠90
−
I1S = − =
= 4,388∠36,87 A
Z1
50∠53,13
−
−
I 3S = 4,388∠156,87 A
I 2 S = 4,388∠ − 83,13 A ;
−
−
V23
V12
380∠120
−
−
I 2T = − = 7,6∠36,87 A
I1T = − =
= 7,6∠156,87 A ;
Z 2 50∠ − 36,87
Z2
− −
−
I1 = I1S + I1T = −3,479 + j 5,618 = 6,608∠121,768 A
− −
−
−
I 2 = I 2 S + I 2T − I1T = 13,594 − j 2,781 = 13,876∠ − 11,562 A
− −
−
I 3 = I 3S − I 2T = −10,115 − j 2,836 = 10,505∠ − 164,338 A
Come si può verificare la somma delle correnti di linea totali è nulla pur
essendo il carico complessivamente squilibrato e quindi le correnti non hanno
moduli uguali e sfasamenti reciproci di 120°.
Ing. Gerardi
**** 10/11/115 17:53:06 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 116
**** CIRCUIT DESCRIPTION
******************************************************************************
*si sceglie w = 2 rad/s per cui
*f = .3183 Hz
*si inseriscono tre generatori relativi alle tensioni di fase
V_E1 1 0 AC 219.3931 90
V_E2 2 0 AC 219.3931 -30
V_E3 3 0 AC 219.3931 210
*per le correnti di linea si inseriscono tre generatori
*di 0V che funzionano da amperometri, per cui si ha
*I1=I(Vamp1), I2=I(Vamp2) e e I3=I(Vamp3)
Vamp1 1 10 AC 0 0
Vamp2 2 20 AC 0 0
Vamp3 3 30 AC 0 0
R10 10 11 30
R20 20 21 30
R30 30 31 30
*le induttanze si calcolano da L = XL/w
L10 11 0 20
L20 21 0 20
L30 31 0 20
R12 10 100 40
R23 20 200 40
*i condensatori si calcolano da C = 1/(w*XC)
C12 100 20 16.6667E-3
C23 200 30 16.6667E-3
.AC LIN 1 .3183 .3183
.PRINT AC I(Vamp1) IP(Vamp1) I(Vamp2) IP(Vamp2)
.PRINT AC I(Vamp3) IP(Vamp3)
.END
**** 10/11/115 17:53:06 ******* Evaluation PSpice (September 1991) ***********
**** SMALL SIGNAL BIAS SOLUTION
TEMPERATURE = 27.000 DEG C
**** AC ANALYSIS
TEMPERATURE = 27.000 DEG C
******************************************************************************
FREQ
I(Vamp1)
IP(Vamp1) I(Vamp2) IP(Vamp2)
3.183E-01 6.608E+00 1.218E+02 1.388E+01 -1.156E+01
FREQ
I(Vamp3) IP(Vamp3)
3.183E-01 1.051E+01 -1.643E+02
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 117
Calcolare le POTENZE totali nel circuito dell’esercizio 116.
Soluzione: Supponendo di aver già ricavato le correnti, precedentemente:
−
−
−
I1S = 4,388∠36,87 A ;
I1S = 4,388∠ − 83,13 A ;
I1S = 4,388∠156,87 A
−
I1T = 7,6∠156,87 A ;
I 2T = 7,6∠36,87 A
− −
−
I1 = I1S + I1T = −3,479 + j 5,618 = 6,608∠121,768 A
− −
−
−
I 2 = I 2 S + I 2T − I1T = 13,594 − j 2,781 = 13,876∠ − 11,562 A
− −
−
I 3 = I 3S − I 2T = −10,115 − j 2,836 = 10,505∠ − 164,338 A
1) con Boucherot:
P1 = R1 ⋅ I12S = 577,636W ;
P2 = R2 ⋅ I12T = 2310,4W
Q1 = + X 1 ⋅ I12S = +770,182VAR ;
Q2 = − X 2 ⋅ I12T = −1732,8VAR
PT = 3 ⋅ P1 + 2 ⋅ P2 = 6353,708W ;
QT = 3 ⋅ Q1 + 2 ⋅ Q2 = −1155,054VAR
ST = PT + jQT = 6363,708 − j1155,054VA
2) con la potenza complessa:
S1S = E1 ⋅ I1*S = 577,662 + j 770,069VA
S 2 S = E2 ⋅ I 2*S = 577,590 + j 770,049VA
S3S = E3 ⋅ I 3*S = 577,532 + j 770,187VA
S1T = V12 ⋅ I1*T = 2310,244 − j1732,860VA
S 2T = V23 ⋅ I 2*T = 2310,4 − j1732,8VA
ST = S1S + S 2 S + S3S + S1T + S 2T = 6353,428 − j1155,355VA
Ing. Gerardi
ESERCIZIO 118
Tre impedenze uguali vengono alimentate da una tensione di linea (V = 400
V efficaci). Calcolare le POTENZE totali quando vengono collegate prima a
stella e poi a triangolo.
Soluzione: Si fa riferimento al sistema di tensioni trifasi dell’esercizio 116
a) collegamento a STELLA:
1
E1 230,94∠90
=
= 4,62∠36,87 A
50∠53,13
Z
E
= 2 = 4,62∠ − 83,13 A
Z
I1S =
2
3
I 2S
I1
30Ω
R
I2
30Ω
R
I3
30Ω
R
E3
= 4,62∠156,87 A
Z
2
Ste = 3 ⋅ R ⋅ I1S = 1,92kW
I 3S =
40Ω
X
40Ω
X
40Ω
X
PT _
QT _ Ste = 3 ⋅ X ⋅ I12S = 2,56kVAR
a) collegamento a TRIANGOLO:
1
2
I12 =
V12 400∠120
= 8∠66,87 A
=
50∠53,13
Z
I 23 =
V23
= 8∠ − 53,13 A
Z
I 31 =
V31
= 8∠ − 173,13 A
Z
3
30Ω
40Ω
I1
I2
I3
I12
I23
I31
R
X
30Ω
40Ω
R
X
30Ω
40Ω
R
X
I1 = I12 − I 31 = 13,86∠36,9 A
I 2 = I 23 − I12 = 13,86∠ − 83,1A
Le correnti di linea e le potenze sono il triplo
I 3 = I 31 − I 23 = 13,85∠156,88 A
rispetto al collegamento a stella.
2
PT _ Tri = 3 ⋅ R ⋅ I 31
= 5,76kW
2
= 7,68kVAR
QT _ Tri = 3 ⋅ X ⋅ I 31
Ing. Gerardi
**** 10/11/115 18:20:42 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 118
**** CIRCUIT DESCRIPTION
*si sceglie w = 2 rad/s (f = .3183 Hz)
V_E1 1 0 AC 230.9401 90
V_E2 2 0 AC 230.9401 -30
V_E3 3 0 AC 230.9401 210
*per le correnti di linea si usano 6 generatori
*di 0V (amperometri): 3 per la stella e 3 triangolo
*CARICO A STELLA
VampS1 1 10 AC 0 0
VampS2 2 20 AC 0 0
VampS3 3 30 AC 0 0
R1S 10 11 30
R2S 20 21 30
R3S 30 31 30
L1S 11 0 20
L2S 21 0 20
L3S 31 0 20
*CARICO A TRIANGOLO
VampT1 1 100 AC 0 0
VampT2 2 200 AC 0 0
VampT3 3 300 AC 0 0
R1T 100 101 30
R2T 200 201 30
R3T 300 301 30
L1T 101 200 20
L2T 201 300 20
L3T 301 100 20
.AC LIN 1 .3183 .3183
.PRINT AC I(VampS1) IP(VampS1) I(VampS2) IP(VampS2)
.PRINT AC I(VampS3) IP(VampS3)
.PRINT AC I(VampT1) IP(VampT1) I(VampT2) IP(VampT2)
.PRINT AC I(VampT3) IP(VampT3)
.END
**** 10/11/115 18:20:42 ******* Evaluation PSpice (September 1991) ***********
**** AC ANALYSIS
TEMPERATURE = 27.000 DEG C
FREQ
I(VampS1) IP(VampS1) I(VampS2) IP(VampS2)
3.183E-01 4.619E+00 3.687E+01 4.619E+00 -8.313E+01
******************************************************************************
FREQ
I(VampS3) IP(VampS3)
3.183E-01 4.619E+00 1.569E+02
******************************************************************************
FREQ
I(VampT1) IP(VampT1) I(VampT2) IP(VampT2)
3.183E-01 1.386E+01 3.687E+01 1.386E+01 -8.313E+01
******************************************************************************
FREQ
I(VampT3) IP(VampT3)
Ing. Gerardi
3.183E-01 1.386E+01 1.569E+02
JOB CONCLUDED
TOTAL JOB TIME
0.00
ESERCIZIO 119
Un sistema di tensioni trifase (V=380V eff.) a 4 fili alimenta questi carichi:
1) carico monofase tra fase 1 e Neutro ( Z1N = 13,15∠34,93Ω );
2) carico monofase tra fase 2 e Neutro ( Z 2 N = 10,41∠21,57Ω );
3) carico trifase equilibrato a stella ( Z S = 11,56∠28,36Ω );
Calcolare le correnti di linea totali e di neutro; calcolare le POTENZE totali.
Soluzione: Si fa riferimento al sistema di tensioni trifasi dell’esercizio 116.
1
2
3
N
I1
I2N =
I2
I3
I1N = 16,68∠55,07 A
IN
Z1N
E2
= 21,07∠ − 51,57 A
Z2N
I1N
Z2N
I2N
Z1S
I1S
I2S
I3S
Z2S
Z3S
I1S = 18,98∠61,64 A
I 2 S = 18,98∠ − 58,36 A
I 3S = 18,98∠ − 178,36 A
I1 = I1N + I1S = 35,82∠58,02 A ;
I 2 = I 2 N + I 2 S = 39,99∠ − 54,78 A
I 3 = I 3S = 18,98∠ − 178,37 A ;
I N = I1N + I 2 N = 25,21∠ − 6,45 A
P1N = R1N ⋅ I12N = 2999,24W ;
P2 N = R2 N ⋅ I 22N = 4297,39W
Q1N = X 1N ⋅ I12N = +2095,01VAR ;
Q2 N = X 2 N ⋅ I 22N = +1700,31VAR
PStella = 3 ⋅ RStella ⋅ I12S = 10990,93W ;
QStella = 3 ⋅ X Stella ⋅ I12S = +5933,16VAR
PTotale = ∑ P = 18287,72W ;
QTotale = ∑ Q = +9728,48VAR
Con la potenza complessa:
STotale _ Triangolo = S1N + S1N + S Stella =
(
)(
) (
)
= E1 ⋅ I1*N + E2 ⋅ I 2*N + 3 ⋅ E1 ⋅ I1*S = 18291,16 + j9728,24VA
Ing. Gerardi
**** 10/14/115 11:33:37 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 119
**** CIRCUIT DESCRIPTION
******************************************************************************
*si sceglie w = 2 rad/s per cui
*f = .3183 Hz
*si inseriscono tre generatori relativi alle tensioni di fase
V_E1 1 0 AC 219.3931 90
V_E2 2 0 AC 219.3931 -30
V_E3 3 0 AC 219.3931 210
*per le correnti si inseriscono 4 generatori di tensione
*di 0V che funzionano da amperometri, per cui si ha
*I1=I(Vamp1), I2=I(Vamp2), I3=I(Vamp3), IN=I(VampN)
Vamp1 1 10 AC 0 0
Vamp2 2 20 AC 0 0
Vamp3 3 30 AC 0 0
VampN 100 0 AC 0 0
R1N 10 11 10.781
L1N 11 100 3.765
R2N 20 21 9.681
L2N 21 100 1.914
R1S 10 111 10.173
L1S 111 100 2.746
R2S 20 222 10.173
L2S 222 100 2.746
R3S 30 333 10.173
L3S 333 100 2.746
.AC LIN 1 .3183 .3183
.PRINT AC I(Vamp1) IP(Vamp1) I(Vamp2) IP(Vamp2)
.PRINT AC I(Vamp3) IP(Vamp3) I(VampN) IP(VampN)
.END
**** AC ANALYSIS
TEMPERATURE = 27.000 DEG C
******************************************************************************
FREQ
I(Vamp1)
IP(Vamp1) I(Vamp2) IP(Vamp2)
3.183E-01 3.560E+01 5.856E+01 3.998E+01 -5.479E+01
******************************************************************************
FREQ
I(Vamp3) IP(Vamp3) I(VampN) IP(VampN)
3.183E-01 1.898E+01 -1.784E+02 2.283E+01 -7.127E+00
JOB CONCLUDED
TOTAL JOB TIME
.05
Ing. Gerardi
ESERCIZIO 120
Un sistema di tensioni trifase (V=380V eff.; f=50 Hz) a 4 fili alimenta un
Impianto industriale con i carichi con i seguenti DATI DI TARGA:
(carico a) 4 M.A.T.: Vn = 400V; Pn = 15 kW; pfn = 0,82; ηn = 0,85;
(carico b) 10 M.A.T.: Vn = 400V; Pn = 2,2 kW; pfn = 0,74; ηn = 0,78;
(carico c) 30 lampade: Vn = 230V; Pn = 36 W; pfn = 1;
(carico d) un forno a induzione: Vn = 400V; Pn = 25 kW; pfn = 0,5;
Rifasare l’impianto per ottenere pf = 0,9 (si supponga che tutti i carichi siano
contemporaneamente attivi ed in condizioni di funzionamento nominale).
Soluzione:Con Boucherot, si calcolano le potenze attive e reattive:
15
= 70588W ;
0,85
Qa = Pa ⋅ tgϕ a = 49271VAR
carico (a)
Pa = 4 ⋅
carico (b)
Pb = 10 ⋅
carico (c)
Pc = 30 ⋅ 36 = 1080W ;
Qc = 0
carico (d)
Pd = 25000W ;
Qd = Pd ⋅ tgϕ d = 43301VAR
2,2
= 28205W ;
0,78
Qb = Pb ⋅ tgϕb = 25636VAR
PTotale = Pa + Pb + Pc + Pd = 124873W
QTotale = Qa + Qb + Qd = 118208VAR
tgϕTotale = QT
(
PT
cos ϕTotale = 0,7262
= 0,9466 ;
)
QC = PTotale ⋅ tgϕTotale − tgϕ I = 57726VAR
C=
QC
3 ⋅ω ⋅ V
2
≅ 383µF
Ing. Gerardi
ESERCIZIO 121
Calcolare la potenza media dissipata dalla resistenza nel circuito in figura.
k = 0, 9
X1
X2
+ j 4Ω
+ j 8Ω
V +
− 40 − j10V
20Ω
R
Soluzione:
I
− j 12Ω
XC
Applicando la KVL nell’unica maglia si ha:
− V + [R + j ⋅ ( X 1 + X 2 − X C + 2 ⋅ X M )] ⋅ I = 0
X M = k ⋅ X 1 ⋅ X 2 = 5,091Ω
I=
40 − j10
= 1,386 − j1,206 = 1,837∠ − 41,017 A
[20 + j ⋅ (4 + 8 − 12 + 10,182)]
Se si invertisse il “puntino di “X2” si ha:
I=
40 − j10
= 1,790 − j 0,412 A
[20 + j ⋅ (4 + 8 − 12 − 10,182)]
La potenza media dissipata dalla resistenza vale:
1
1
⋅ R ⋅ I 2 = ⋅ 20 ⋅1,837 2 = 33,75W
2
2
Oppure si calcola dalla potenza complessa:

1
PR = Re S generatore = Re  ⋅V ⋅ I *  = 33,75W

2
PR =
[
]
**** 10/08/115 17:29:26 ******* Evaluation PSpice (September 1991) ***********
V 1 0 AC 41.231 -14.036
L1 1 2 2
L2 2 3 4
K12 L1 L2 .9
C 3 4 41.6667E-3
R 4 0 20
.AC LIN 1 .3183 .3183
.PRINT AC I(R) IP(R)
.END
**** 10/08/115 17:29:26 ******* Evaluation PSpice (September 1991) ***********
FREQ
I(R)
IP(R)
3.183E-01 1.837E+00 -4.102E+01
**** 10/08/115 17:29:26 ******* Evaluation PSpice (September 1991) ***********
Ing. Gerardi
ESERCIZIO 122
Calcolare la tensione v(t) nel circuito in figura, funzionante in regime
sinusoidale (f = 50 Hz). (Valori efficaci).
5Ω
R
20
30 V +
− VS
◦
XC
k = 0, 9
−j2Ω
IS
+j4Ω
+j5Ω
8 0◦ A
v(t)
Soluzione:
X M = k ⋅ X 1 ⋅ X 2 = 4,025Ω
Applicando il metodo degli anelli si ha:
1) maglia SX I1 verso orario:
− VS + (R + jX 1 ) ⋅ I1 − jX M ⋅ I S = 0
2) maglia DX IS verso antiorario:
I1 =
− V + j ( X 2 − X C ) ⋅ I S − jX M ⋅ I1 = 0
VS + jX M ⋅ I S
= 6,229 + j 3,456 A
(R + jX 1 )
V = 13,912 − j1,073 = 13,954∠ − 4,411°V
Passando nel dominio del tempo:
ω = 2 ⋅ π ⋅ f = 314,16 rad s
Vm = 2 ⋅ V = 2 ⋅13,954 = 19,734V
v(t ) = 19,734 ⋅ cos(314,16 ⋅ t − 4,411°)V
**** 10/08/115 17:35:45 ******* Evaluation PSpice (September 1991) ***********
VS 1 0 AC 20 30
R1 1 2 5
L1 2 0 2
L2 0 3 2.5
K12 L1 L2 .9
C 3 4 .25
Rinf 3 4 1E12
IS 0 4 AC 8 0
.AC LIN 1 .3183 .3183
.PRINT AC IR(R1) II(R1) V(4) VP(4)
.END
**** 10/08/115 17:35:45 ******* Evaluation PSpice (September 1991) ***********
FREQ
IR(R1)
II(R1)
V(4)
VP(4)
3.183E-01 6.229E+00 3.456E+00 1.395E+01 -4.410E+00
**** 10/08/115 17:35:45 ******* Evaluation PSpice (September 1991) ***********
Ing. Gerardi
ESERCIZIO 123
Determinare l’equivalente di Thèvenin ai terminali “a” e “b” del circuito in
figura. (Valori efficaci).
+j2Ω
+j6Ω
5Ω
+j8Ω
−j3Ω
a
◦
E1 +
− 10 90 V
2Ω
4 0◦ A
I0
b
Soluzione:
Si trasforma in una rete a “T”:
5Ω
+j4Ω
+j3Ω
2Ω
+j2Ω
◦
E1 +
− 10 90 V
a
8 0◦ V +
− E0
b
Calcolo di ZTH (si passivizza la rete)
ZTH = j 2 +
(5 + j 4) ⋅ (2 + j3) = 1,5 +
(5 + j 4) + (2 + j 3)
j 3,786 = 4,072∠68,387Ω
Calcolo di ETH
Nella maglia circola una corrente oraria pari a:
I=
(10∠90) − (8∠0) = 0,143 +
(5 + j 4) + (2 + j3)
j1,286 A
ETH = Vab = (10∠90) − (5 + j 4 ) ⋅ I = 4,429 + j 2,998 = 5,348∠34,094V
Verifica della ETH :
ETH = Vab = (8∠0 ) + (2 + j 3) ⋅ I = 4,428 + j 3,001 = 5,349∠34,127V
Ing. Gerardi
**** 10/11/115 20:44:38 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 123a - Calcolo E_TH
**** CIRCUIT DESCRIPTION
******************************************************************************
*si sceglie w = 2 rad/s (f = .3183 Hz)
V_E1 1 0 AC 10 90
R1 1 2 5
L1 2 3 3
L2 4 3 4
*k= M/radq(L1*L2) = 0,288675
K12 L1 L2 .288675
C 4 5 166.6667E-3
R2 5 0 2
I0 0 5 AC 4 0
*la tensione E_TH la V(3)
.AC LIN 1 .3183 .3183
.PRINT AC V(3) VP(3)
.END
**** 10/11/115 20:44:38 ******* Evaluation PSpice (September 1991) ***********
**** AC ANALYSIS
TEMPERATURE = 27.000 DEG C
******************************************************************************
FREQ
V(3)
VP(3)
3.183E-01 5.349E+00 3.411E+01
**** 10/11/115 20:44:40 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 123b - Calcolo Z_TH
**** CIRCUIT DESCRIPTION
*si spengono i generatori azzerandoli
*si inserisce un genertatore da 1A e si
*misura la sua tensione che la Z_TH
V_E1 1 0 AC 0 0
R1 1 2 5
L1 2 3 3
L2 4 3 4
I 0 3 AC 1 0
*k= M/radq(L1*L2) = 0,288675
K12 L1 L2 .288675
C 4 5 166.6667E-3
R2 5 0 2
I0 0 5 AC 0 0
.AC LIN 1 .3183 .3183
.PRINT AC V(3) VP(3)
.END
**** 10/11/115 20:44:40 ******* Evaluation PSpice (September 1991) ***********
**** AC ANALYSIS
TEMPERATURE = 27.000 DEG C
******************************************************************************
FREQ
V(3)
VP(3)
Ing. Gerardi
3.183E-01 4.072E+00 6.838E+01
ESERCIZIO 124
Calcolare la potenza media dissipata dalla resistenza da ZS.
ZP
I1
1 : 10
3 + j4Ω
120 0◦ V ef f. +
− VS
+
I2
+
V2
V1
−
ZS
500 − j200Ω
−
Soluzione: 1) applicando la KVL al primario ed al secondario si ricava:
− VS + (3 + j 4 ) ⋅ I 1 + V1 = 0
− V2 + Z 2 ⋅ I 2 = 0
Dall’analisi delle tensioni e correnti relative ai “puntini”, si ha :
V2 = −n ⋅ V1

 I1 = −n ⋅ I 2
− VS − (3 + j 4 ) ⋅ n ⋅ I 2 − 1 ⋅V2 = 0
n

− V2 + Z 2 ⋅ I 2 = 0
Risolvendo rispetto a I2 si ricava:
I2 =
− 1200
= 1,455∠165 ,964 A
800 + j 200
2) risolvendo con il metodo agli anelli:
1) KVL maglia SX IA (orario):
− 120 + (3 + j 4 ) ⋅ I1 + V1 = 0
2) KVL maglia DX IB (antiorario):
− V2 + (500 − j 200) ⋅ I 2 + = 0
V1 = 63,54 − j 45,89V

V2 = −635,4 + j 458,9V

 I1 = 14,12 − j 3,53 A
 I = −1,412 + j 0,353 A
 2
La potenza media dissipata da ZS vale:
Oppure:
PS = 500 ⋅ I 22 = 1058,51W
PS = 5 ⋅ I12 = 1059,18W
Ing. Gerardi
ESERCIZIO 125
Calcolare la corrente ICC (cortocircuito tra 2 punti),per il circuito in figura.
10Ω
8A
20Ω
Icc
50Ω
40Ω
Soluzione: Metodo agli anelli: Ci sono 31 correnti di anello Ia, Ib e Ic.
1) Vincolo sul generatore
10Ω
8A
Ia
2) KVL maglia Ib oraria: + 30 ⋅ I b − 10 ⋅ I a = 0
20Ω
Ib
3) KVL maglia Ic oraria: + 90 ⋅ I c − 50 ⋅ I a = 0
Icc
50Ω
Ia = 8A
Ia = 8A
40Ω
Ic
Ib = 8 A
3
I c = 40 A
9
I cc = I c − I b = 1,778 A
1
2) Metodo nodale Si prende il nodo B come riferimento:
A
I1
I2
10Ω
8A
1) KCL nodo A
−8+
EA EA
+
=0
10 20
2) KCL nodo C
+8+
EC EC
+
=0
50 40
20Ω
B
I3
Icc
50Ω
I4
40Ω
 E A = +53,333V
; I1 = E A = +5,333 A

10
 E C = −177,778V
C
I2 =
EA
20
= +2,667 A ; I 3 = −
I cc = I1 − I 3 = +1,777 A
EC
50
= +3,556 A ; I 4 = −
EC
40
= +4,444 A
KCL al nodo B a sinistra
Ing. Gerardi
**** 10/14/115 08:40:24 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 125
****
CIRCUIT DESCRIPTION
******************************************************************************
I0 0 1 DC 8
R1 1 2 10
R2 2 0 50
R3 1 3 20
R4 3 0 40
*per la corrente Icc si inserisce un generatore
*di 0V che funziona da amperometro: Icc=I(Vamp)
Vamp 2 3 DC 0
*Ib = I(R3) e Ic = I(R4)
.DC I0 8 8 1
.PRINT DC I(Vamp) I(R3) I(R4)
.END
**** 10/14/115 08:40:24 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 125
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
I0
I(Vamp)
I(R3)
I(R4)
8.000E+00 1.778E+00 2.667E+00 4.444E+00
JOB CONCLUDED
TOTAL JOB TIME
.05
Ing. Gerardi
ESERCIZIO 126
Calcolare la tensione E0 (ramo aperto),per il circuito in figura.
10Ω
8A
20Ω
+
E0
−
50Ω
40Ω
Soluzione:
A
10Ω
8A
B
10Ω
20Ω
+
E0
−
50Ω
D
8A
+
Ia
40Ω
20Ω
50Ω
E0
−
Ib
40Ω
C
1) Metodo nodale
2) Metodo agli anelli
Metodo nodale
1) KCL nodo A: − 8 + 0,1 ⋅ (E A − E B ) + 0,05 ⋅ (E A − E D ) = 0
2) KCL nodo B: + 0,1 ⋅ (E B − E A ) + 0,02 ⋅ E B = 0
3) KCL nodo D: + 0,05 ⋅ (E D − E A ) + 0,025 ⋅ (E D ) = 0
E0 è la differenza dei potenziali dei nodi B e D:
 E A = +240V

 E B = +200V
 E = +160V
 D
E0 = E B − E D = +40V
I a = 8 A

I b = 4 A
Metodo agli anelli
1) Vincolo sul generatore I a = 8 A
2) KVL maglia Ib (oraria): + 120 ⋅ I b − 60 ⋅ I a = 0
Applicando la KVL alle maglia sotto (e per verifica alla maglia sopra), si ha:
E0 = VBC − VDC = [50 ⋅ (I b − I a )] − (40 ⋅ I a ) = 40V
(maglia “in
basso”)
Ing. Gerardi
**** 10/14/115 08:45:00 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 126
****
CIRCUIT DESCRIPTION
******************************************************************************
I0 0 1 DC 8
R1 1 2 10
R2 2 0 50
R3 1 3 20
R4 3 0 40
*la tensione E0 uguale a V(2,3)
*EA = V(1), EB = V(2), ED = V(3)
.DC I0 8 8 1
.PRINT DC V(2,3)
.PRINT DC V(1) V(2) V(3)
.END
**** 10/14/115 08:45:00 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 126
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
I0
V(2,3)
8.000E+00 4.000E+01
**** 10/14/115 08:45:00 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 126
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
I0
V(1)
V(2)
V(3)
8.000E+00 2.400E+02 2.000E+02 1.600E+02
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 127
Calcolare la tensione V, nel circuito in figura con sovrapposizione degli effetti.
12Ω
+ V −
10Ω
20Ω
40Ω
8A
50V +
−
40V +
−
Soluzione: Sovrapposizione degli effetti
A
10Ω
40Ω
12Ω
+ VI −
20Ω
50V +
−
B
A
12Ω
+ V II −
A
B
20Ω
8Ω
C
+V
III
−
12Ω Iy
8Ω
+ 40V
−
C
B
20Ω
8A
C
• 1^ effetto: agisce il gen. 50 V Col partitore di tensione (figura a sinistra) :
V ⋅ 12
50 ⋅ R X
= 32V ;V I = AC
= +12V
R X = 40 // (12 + 20) = 160 Ω ;V AC =
9
R X + 10
12 + 20
• 2^ effetto: agisce il gen. 40 V Col partitore di tensione (figura al centro):
V II = −40 ⋅
12
= −12V
12 + 20 + (40 // 10)
• 3^ effetto: agisce il gen. 8 A Col partitore di corrente (figura a destra):
Iy = 8⋅
20
= 4 A V III = − I y ⋅ 12 = −48V
20 + [12 + (40 // 10 )]
• Sommando gli effetti si ha:
V = V I + V II + V III = −48V
Ing. Gerardi
**** 10/14/115 08:53:19 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 127
****
CIRCUIT DESCRIPTION
******************************************************************************
R1 1 0 40
R2 1 2 10
V3 2 0 DC 50
R4 1 3 12
R5 3 4 20
V6 4 0 DC 40
I7 0 3 DC 8
*la tensione V uguale a V(1,3)
.DC V3 50 50 1
.PRINT DC V(1,3)
.END
**** 10/14/115 08:53:19 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 127
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V3
5.000E+01
V(1,3)
-4.800E+01
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 128
Calcolare la tensione V, nel circuito in figura con Thèvenin e Norton.
12Ω
+ V −
10Ω
20Ω
40Ω
8A
50V +
−
40V +
−
RTH = RNO = 20 + (40 // 10 ) = 28Ω
Soluzione: 1) Thèvenin:
 50 ⋅ 40 
ETH = V AC − VBC = 
 − (40 + 8 ⋅ 20 ) = −160V
+
40
10


- Calcolo di ETH
A
+
B
−
ET H
10Ω
RT H
40Ω
8A
50V +
−
A
28Ω
20Ω
ET H
40V +
−
+
−
−160V
+
12Ω
V
−
B
C
V =
ETH ⋅ 12
= −48V
RTH + 12
1
2) Norton:- Calcolo di INO. Con il metodo nodale
si calcola la tensione nodale EA.
A
IN O
B
I2
I1
10Ω
A
20Ω
40Ω
8A
50V +
−
40V +
−
+
IN O
−
40
A
7
RN O
C
− 8 + 0,025 ⋅ E A + 0,1 ⋅ (E A − 50) + 0,05 ⋅ (E A − 40 ) = 0
12Ω
28Ω
V
−
B
E A = 85,714V
I NO = − I1 − I 2 = −0,025 ⋅ E A − 0,1 ⋅ (E A − 50) = −5,714 A
V = I NO ⋅ (RNO // 12) = −48V
Ing. Gerardi
**** 10/14/115 09:02:41 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 128a - calcolo RTH = RNO
**** CIRCUIT DESCRIPTION
******************************************************************************
*si passivizza il circuito e si inserisce al posto
*della resistenza da 12 ohm un generatore di 1A
*la cui tensione uguale a RTH
R1 1 0 40
R2 1 2 10
V3 2 0 DC 0
I 3 1 DC 1
R5 3 4 20
V6 4 0 DC 0
I7 0 3 DC 0
.DC I 1 1 1
.PRINT DC V(1,3)
.END
**** DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
I
V(1,3)
1.000E+00 2.800E+01
JOB CONCLUDED
TOTAL JOB TIME
0.00
**** 10/14/115 09:02:44 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 128b - calcolo ETH
**** CIRCUIT DESCRIPTION
******************************************************************************
*la tensione E_TH la tensione a vuoto cio V(1,3)
R1 1 0 40
R2 1 2 10
V3 2 0 DC 50
R5 3 4 20
V6 4 0 DC 40
I7 0 3 DC 8
*la tensione V uguale a V(1,3)
.DC V3 50 50 1
.PRINT DC V(1,3)
.END
**** DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V3
V(1,3)
5.000E+01 -1.600E+02
JOB CONCLUDED
Ing. Gerardi
TOTAL JOB TIME
0.00
**** 10/14/115 09:10:51 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 128c - calcolo INO
****
CIRCUIT DESCRIPTION
******************************************************************************
*per la corrente INO si inserisce un resistore
*molto piccolo che funziona da amperometro: INO = I(RS)
R1 1 0 40
R2 1 2 10
V3 2 0 DC 50
RS 1 3 1e-12
R5 3 4 20
V6 4 0 DC 40
I7 0 3 DC 8
.DC V3 50 50 1
.PRINT DC I(RS)
.END
ÿ
**** 10/14/115 09:10:51 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 128c - calcolo INO
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V3
I(RS)
5.000E+01
-5.713E+00
JOB CONCLUDED
TOTAL JOB TIME
0.00
ESERCIZIO 129
Calcolare la tensione V, nel circuito in figura con Thèvenin e Norton.
3A
10Ω
20Ω
c
a
+
40V +
−
40Ω
V
18Ω
−
b
Soluzione:
1) Thèvenin: si taglia il ramo “interessato” dalla tensione.
Calcolo RTH. Si passivizza il circuito. RTH = 20 + (10 // 40 ) = 28Ω
3A
Calcolo ETH . È la tensione a vuoto.
KVL alla maglia in basso a destra:
10Ω
40 

ETH = Vac + Vcb = (20 ⋅ 3) +  40 ⋅  = +92V
50 

40V +
−
40Ω
a
+
ET H
−
b
RT H
Equivalente di Thèvenin si trova la
a
28Ω
tensione V col partitore di tensione:
V = ETH
20Ω
c
+
ET H +
− 92V
18
92 ⋅18
= +36V
⋅
=
18 + RTH 18 + 28
V
18Ω
−
b
2) Norton: si taglia il ramo “interessato”.Calcolo RNO. RNO = RTH = 28Ω
Calcolo INO .Col metodo degli anelli. [KVL maglie Ia e Ic e vincolo gen.]
− 40 + 50 ⋅ I a − 40 ⋅ I c = 0 ; + 60 ⋅ I c − 40 ⋅ I a − 20 ⋅ I b = 0 ; I b = 3 A
3A
10Ω
40V +
−
Ia
c
20Ω
a
Ic
40Ω
b
a
Ib
IN O
IN O
23
A
7
Ic =
+
RN O
28Ω
V
−
b
18Ω
23
A = I NO
7
 R ⋅ 18 
 = +36V
V = I NO ⋅  NO
 RNO + 18 
Ing. Gerardi
**** 10/14/115 11:45:56 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 129
****
CIRCUIT DESCRIPTION
******************************************************************************
V1 1 0 DC 40
R2 1 2 10
R3 2 0 40
R4 2 3 20
I5 2 3 DC 3
R6 3 0 18
*la tensione V uguale a V(R6)
.DC V1 40 40 1
.PRINT DC V(R6)
.END
ÿ
**** 10/14/115 11:45:56 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 129
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V1
4.000E+01
V(R6)
3.600E+01
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO 130
Calcolare la corrente i, nel circuito in figura con Norton e Sovrapposizione.
6Ω
12V
+−
i
2A
4Ω
5Ω
4A
Soluzione:1) Norton:Calcolo RNO. Si passivizza.
RNO = 6 + 4 = 10Ω
Calcolo INO . È la corrente del cortocircuito. col metodo degli anelli.
12V
6Ω
2A
+−
4Ω
IN O
Ia
4A
Ib
Ic
I b = −0,4 A
3.6A
RN O
10Ω
6Ω
Ia = 2A
vincolo gen. 4 A
Ic = 4 A
4Ω
RNO
= +2,4 A
RNO + 5
2^effetto:gen.(12 V) 3^ effetto: gen.(4 A)
12V
i
I
6Ω
5Ω
4Ω
iI = 2 ⋅
vincolo gen. 2 A
i = I NO ⋅
5Ω
2) Sovrapposizione:
1^ effetto: gen. (2 A)
2A
+ 10 ⋅ I b − 4 ⋅ I a + 12 = 0
I NO = I b + I c = +3,6 A . Equivalente di Norton:
i
IN O
KVL maglia Ib
6Ω
+−
iII
4Ω
iIII
5Ω
4A
5Ω
4
− 12
(6 + 4) = + 8 A
4
8
= − A i III = 4 ⋅
= + A i II =
6+4+5
5
4 + (6 + 5)
15
(6 + 4) + 5 3
Sommando gli effetti si ottiene infine:
i = i I + i II + i III =
8 4 8
− + = 2,4 A
15 5 3
Ing. Gerardi
**** 10/15/115 17:32:27 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 130
**** CIRCUIT DESCRIPTION
******************************************************************************
I1 0 1 DC 2
R2 1 0 4
R3 1 2 6
V3 2 3 DC 12
R4 3 0 5
I5 0 3 DC 4
*la corrente "i" uguale a I(R4)
.DC I1 2 2 1
.PRINT DC I(R4)
.END
**** 10/15/115 17:32:27 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 130
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
*****************************************************************************
I1
I(R4)
2.000E+00 2.400E+00
JOB CONCLUDED
TOTAL JOB TIME
0.00
*PER OTTENERE 3 EFFETTI DAL CIRCUITO SI SIMULA
*3 VOLTE (ANNULLANDO 2 GENERATORI PER VOLTA).
****** 1^ EFFETTO ******
I1
I(R4)'
2.000E+00 5.333E-01
****** 2^ EFFETTO ******
V3
I(R4)''
1.200E+01 -8.000E-01
****** 3^ EFFETTO ******
I5
I(R4)'''
4.000E+00 2.667E+00
Ing. Gerardi
ESERCIZIO 131
Determinare la corrente i(t) pet t ≥ 0, nel circuito in figura se i(0) = 2A.
i
6H
10Ω
0.5 · i
40Ω
I I = i (0 ) = 2 A
Soluzione: (Con Thèvenin). Il valore iniziale è:
Il valore finale IF e τ si calcolano dal circuito equivalente di Thèvenin:
E
+ 1 + 0,5 ⋅ (− 1) + A = 0
Calcolo RTH.
KCL nodo A
40
1A
E A = −20V
A
−
+
KVL maglia SX:
i
v0
+
− E A − v0 + (10 ⋅ 1) = 0
10Ω
eA
40Ω
v0 = +30V
− 0.5 · i
V
RTH = 0 = 30Ω
1
Calcolo ETH. Non c’è generatori indipendenti, per cui:
+
ET H
1
ETH = 0V
−
i=0
10Ω
0.5 · i
40Ω
Dal circuito equivalente di Thèvenin si ricavano:
I F = ETH
= 0A
RTH
τ = L R = 0,2 sec
TH
Quindi si ha:
i (t ) = I F + (I I − I F ) ⋅ e
−t
τ
= 2 ⋅ e − 5⋅t A
Ing. Gerardi
ESERCIZIO 132
Calcolare la potenza del generatore indipendente nel circuito in figura.
10Ω
A
20Ω
B
+
V2
2
90V +
−
30Ω
V2
60Ω
−
AI
BI
Soluzione:
Si risolve con i metodo agli anelli, e si verifica con il bilancio delle potenze.
1) Anelli. Si scrivono 3 KVL ed 1 vincolo sul generatore controllato.
A
10Ω
+
IA
90V +
−
20Ω
Vx
AI
I A = 6,6 A ;
−
V2
2
B
IB
− 90 + 10 ⋅ I A + Vx = 0
KVL maglia IB
+ 50 ⋅ I B + Vx − 30 ⋅ I C = 0
KVL maglia IC
+ 90 ⋅ I C − 30 ⋅ I B = 0
vincolo gen.
I A + I B = V2 2 = −30 ⋅ I C
+
IC
30Ω
KVL maglia IA
V2
60Ω
−
BI
I B = −0,6 A ;
I C = −0,2 A ;
Vx = 24V
Verifica con il Bilancio delle potenze (convenzione degli utilizzatori)
P10Ω = 10 ⋅ I A2 = +435,6W ; P20Ω = 20 ⋅ I B2 = +7,2W ;
P30Ω = 30 ⋅ (I C − I B )2 = +4,8W P60Ω = 60 ⋅ I C2 = +2,4W
Pgen _ indipendente = Vgen ⋅ I gen = 90 ⋅ I A = −594W (negativa perché erogata)
Pgen _ controllato = Vx ⋅ (I A + I B ) = 24 ⋅ 6 = +144W (positiva perché assorbita)
Risulta quindi verificato che:
Ptotale _ utilizzatori + Ptotale _ generatori = +450 − 450 = 0W
Ing. Gerardi
**** 10/16/115 09:54:49 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 132
****
CIRCUIT DESCRIPTION
******************************************************************************
V1 1 0 DC 90
R2 1 2 10
G3 2 0 3 0 .5
R4 3 2 20
R5 3 0 30
R6 0 3 60
*la corrente del generatore uguale a IA=I(R2)
*la corrente IB uguale a I(R4)
*la corrente IC uguale a I(R6)
.DC V1 90 90 1
.PRINT DC I(R2) I(R4) I(R6)
.END
**** 10/16/115 09:54:49 ******* Evaluation PSpice (September 1991) ***********
* Esercizio 132
****
DC TRANSFER CURVES
TEMPERATURE = 27.000 DEG C
******************************************************************************
V1
I(R2)
I(R4)
I(R6)
9.000E+01 6.600E+00 -6.000E-01 -2.000E-01
JOB CONCLUDED
TOTAL JOB TIME
0.00
Ing. Gerardi
ESERCIZIO
133
Ing. Gerardi
ESERCIZIO
134
Ing. Gerardi
ESERCIZIO
135
Ing. Gerardi
ESERCIZIO
136
Ing. Gerardi
Ing. Gerardi
ESERCIZIO
137
Ing. Gerardi
ESERCIZIO
138
Ing. Gerardi
ESERCIZIO 139
Ing. Gerardi
ESERCIZIO 140
Ing. Gerardi
Ing. Gerardi
ESERCIZIO
141
Ing. Gerardi
ESERCIZIO 142
Ing. Gerardi
ESERCIZIO
143
Ing. Gerardi
ESERCIZIO
144
Ing. Gerardi
ESERCIZIO
145
Ing. Gerardi
ESERCIZIO 146
Ing. Gerardi
Ing. Gerardi
ESERCIZIO
147
Ing. Gerardi
Ing. Gerardi
Ing. Gerardi
ESERCIZIO
148
Ing. Gerardi
ESERCIZIO
149
Ing. Gerardi
ESERCIZIO
150
Ing. Gerardi
ESERCIZIO
151
Ing. Gerardi
ESERCIZIO
152
Ing. Gerardi
Ing. Gerardi
Ing. Gerardi
ESERCIZIO
153
Ing. Gerardi
Ing. Gerardi
ESERCIZIO
154
Ing. Gerardi
ESERCIZIO
155
Ing. Gerardi
ESERCIZIO
156
Ing. Gerardi
ESERCIZIO
157
Ing. Gerardi
ESERCIZIO
158
Ing. Gerardi
ESERCIZIO
159
147
Ing. Gerardi
Ing. Gerardi
ESERCIZIO
160
148
Ing. Gerardi
ESERCIZIO
161
Ing. Gerardi
Ing. Gerardi