Esercitazione 11: Fibre ottiche

Esercitazione 11: Fibre ottiche
GENERALITÀ
Si riassumono brevemente le caratteristiche ben note delle fibre ottiche. Tre sono i tipi di fibre
di uso più comune:
a) le fibre step index (il termine step-index si riferisce al fatto che la fibra presenta una variazione
brusca di indice di rifrazione tra core e cladding) a singolo modo; il diametro del core è di alcuni
µm);
b) le fibre step index multimodo; il diametro del core è di diverse decine di µm ed il termine
multimodo usualmente significa decine o centinaia di modi;
c) le fibre graded index; l'indice di rifrazione presenta una variazione graduale, di tipo parabolico, entro il core. Sono multimodali, ma con alcuni vantaggi nelle prestazioni comunicazionistiche
rispetto al tipo b).
Occorre tener presente che, nel caso comune di fibre ottiche dotate di simmetria circolare, il termine singolo modo è un poco improprio; in effetti vi saranno almeno due modi corrispondenti alle
due possibili polarizzazioni ortogonali. Comunque solo in specifiche applicazioni è indispensabile
l'operazione strettamente a singolo modo. Tale funzionamento richiede fibre con caratteristiche
elettromagnetiche non dotate di simmetria circolare; ciò si realizza con un core ellittico, oppure
inducendo nella fibra delle tensioni interne in fase costruttiva in modo da renderla anisotropa.
È opportuno richiamare brevemente le caratteristiche delle fibre ottiche che ne rendono interessante l'uso. In sostanza si segnalano i seguenti pregi:
- isolamento elettrico: le fibre, almeno quelle più comuni, sono ottimi isolanti elettrici; oltre a
semplificare i problemi di connessioni, ciò implica un facile uso anche in ambienti elettricamente
difficili o pericolosi; l'uso delle fibre, però, non consente (se necessario o utile) il trasporto di alimentazioni elettriche;
- le fibre sono ampiamente insensibili alle perturbazioni elettromagnetiche (a meno di utilizzare
effetti appositi): oltre a introdurre un fattore di sicurezza (e di segretezza), ciò le rende particolarmente indicate nell'uso in ambienti elettromagneticamente inquinati o pericolosi;
- buona resistenza alle radiazioni ionizzanti;
- ridotta sensibilità alle vibrazioni;
- temperature di lavoro anche relativamente elevate;
- piccolo peso ed ingombro;
- facilità d'interfacciamento con componenti optoelettronici discreti e/o integrati; questa proprietà può non essere di immediata applicazione su ampia scala, ma va tenuta ben presente in vista
dell'evoluzione della tecnologia;
- grande larghezza di banda utilizzabile: ciò consente un uso "intensivo" della connessione in fibra ottica, sfruttando tecniche diverse di multiplazione e di demultiplazione (multiplazione temporale, in lunghezza d'onda, ecc.).
I materiali utilizzati per la realizzazione delle fibre hanno un ruolo sostanziale nel definirne le
prestazioni. Tra queste, la più significativa è l'attenuazione [l'attenuazione, di solito misurata in
decibel e riferita ad un km (dB/km), indica di quanto si riduce la potenza ottica durante la propagazione. La misura in dB è espressa da 10 volte il logaritmo (in base 10) del rapporto delle potenze],
legata all'assorbimento ottico dei materiali; tale parametro influenza pesantemente la gamma di lun1
ghezze d'onda in cui è possibile utilizzare un certo tipo di fibra. Le fibre più comuni sono realizzate
con i seguenti materiali:
- le fibre ottiche in silice sono le più usate per le telecomunicazioni; il materiale è ben purificato,
in modo da ridurre drasticamente i picchi di assorbimento dovuti ad impurezze indesiderate, e successivamente drogato (ad es. con Ge) per avere la dovuta variazione di indice di rifrazione. Le regioni di lunghezza d'onda di uso tipico sono centrate sui minimi di attenuazione, intorno ad 1,3 µm
(≈ 0,35 dB/km) e 1,55 µm (≈ 0,2 dB/km); possono però venire ben utilizzate (atten. superiore di un
fattore 10) nell'intervallo 0,5 < λ < 2 µm;
- le fibre ottiche plastiche (di vario tipo) presentano valori di attenuazione anche 1000 volte
maggiori di quelle in silice e non sono ovviamente interessanti per le telecomunicazioni a grande
distanza; ma tollerano raggi di curvatura decisamente più bassi (adatte a percorsi tortuosi) ed hanno
costo molto inferiore;
- le fibre in vetri fluorurati (in fase avanzata di sviluppo; ancora costose e con prestazioni limitate) permettono di lavorare fino a circa 5 µm; mentre vetri più complessi ed i materiali calcogenuri
dovrebbero, in un prossimo futuro, consentire di raggiungere lunghezze d'onda di 10-12 µm. Questa
estensione verso l'alto della regione di lunghezze d'onda in cui sono praticamente utilizzabili le fibre
ottiche è di grande interesse, non solo per le telecomunicazioni ma anche per i sensori in fibra ottica.
PARAMETRI SIGNIFICATIVI
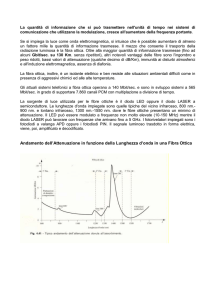
- ATTENUAZIONE. Come già indicato, questo è un parametro primario per caratterizzare le
fibre; esso è di sommo rilievo per le telecomunicazioni a grande distanza. È noto che le fibre in silice presentano diversi minimi di attenuazione al variare della lunghezza d'onda; il minimo assoluto è
localizzato vicino a λ ≈ 1,55 µm, un valore molto basso si realizza anche intorno a λ ≈ 1,33 µm. In
un sistema limitato solo dall'attenuazione, la relazione tra potenza d'ingresso Pi, potenza d'uscita Pu,
lunghezza di tratta L e costante d'attenuazione α (m-1, in ampiezza) è:
Pu/Pi = exp[ -2 α L]
È molto semplice l'uso numerico della precedente relazione. Ad es. con d'attenuazione α = 0,3
dB/km, Pi = 1 mW, Pu minima ricevibile = 0,3 µW risulta un valore massimo di L pari a 102,5 km.
- DISPERSIONE. È il fenomeno che causa la distorsione dei segnali, a seguito della propagazione, se la velocità di gruppo non è costante al variare della frequenza (nella banda di interesse)[ Si
discuterà brevemente il problema per il caso monomodale; in una fibra multimodale il comportamento è più complesso e dominato dalla differenza delle velocità di propagazione tra i vari modi;
pertanto è considerevole il vantaggio delle fibre a singolo modo, sotto l'aspetto in esame]. Le conseguenze sistemistiche di tale fenomeno dipendono dal tipo di modulazione e non conviene discuterle
in generale. Nel caso di modulazione ad impulsi di potenza (tutto o niente), tipicamente usata negli
attuali sistemi di comunicazione in fibra ottica, la distorsione si manifesta come un allargamento
dell'impulso crescente con la lunghezza della tratta propagativa. Ciò è dovuto alla diversa velocità
con cui si propagano le componenti spettrali del segnale a seguito della dispersione (lo spettro del
segnale è determinato sia dalla modulazione, sia dalla larghezza spettrale dell'onda, idealmente monocromatica, erogata dalla sorgente ottica; purtroppo i laser a semiconduttore, anche se in corso di
perfezionamento, presentano problemi per la larghezza spettrale del segnale emesso).
Ovviamente, considerando ad es. un segnale codificato, l'allargamento del singolo impulso a seguito della propagazione rende difficile separare in uscita impulsi adiacenti; per ovviare a ciò è necessario limitare o la capacità di trasmissione (cioè la spaziatura temporale degli impulsi) o la lun2
ghezza della tratta secondo criteri dettati da opportuni compromessi relativi alle prestazioni del sistema.
La dispersione è usualmente caratterizzata dal parametro:
D = (dτ/dλ)/L [ps/nm*km]
in cui τ= L/vg è il ritardo di gruppo. Ovviamente, se vg è costante, D = 0; altrettanto chiaramente D
è un buon indice del fenomeno di dispersione solo ove D = 0, altrimenti è richiesta un'analisi più
complessa. È noto che le fibre in silice presentano un minimo della dispersione nelle vicinanze λ
≈1,3 µm (da ciò l'interesse per questa regione di λ); però, con un'appropriata struttura della fibra
ottica (composizione e variazione radiale dell'indice di rifrazione) si possono ottenere situazioni
molto variate, sia con spostamento della zona di ottimo, sia con un andamento appiattito di D al
variare di λ.
LE FIBRE COME SENSORI
Le fibre trovano ampio e crescente impiego nel campo dei sensori secondo due modalità diverse:
- come elementi per la trasmissione dell'informazione raccolta tramite altri sensori (sensori
estrinseci), - sfruttando la sensibilità della fibra, con eventuale trattamento opportuno, all' ambiente
(sensori intrinseci). Nel primo caso sono significative le prestazioni comunicazionistiche già discusse nel par. precedente. Nel secondo caso, si possono ricordare le seguenti caratteristiche addizionali:
- eventuale misura distribuita, con possibilità di localizzazione spaziale: è un considerevole pregio connesso con la fibra operante direttamente come sensore,
- basso livello di potenza ottica: di solito è talmente basso da non generare problemi anche
in ambienti esplosivi o altrimenti pericolosi,
- la misura per via ottica risulta poco intrusiva e, almeno nella regione a bassa attenuazione, può essere effettuata anche a grande distanza,
- la misura per via ottica può essere molto sensibile (usando la tecnica appropriata).
Sono ormai molto numerose e parecchio diversificate le aplicazioni delle fibre nel campo dei
sensori. Basterà qui ricordare: i giroscopi; gli elementi sensibili a pressioni, sforzi, deformazioni,
vibrazioni; i sensori di campi elettrici, magnetici o i misuratori di correnti; strumenti per rilievo
delle distribuzioni di velocità; l'uso per la misura delle temperature; in diagnostica nucleare; i sensori di composizione chimica (spettrofotometria, ecc.) a scopo industriale, per applicazioni medicobiologiche o per controllo ambientale; ecc..
Alcuni richiami e relazioni utili
In una fibra step index (indice di rifrazione del core n1 e del cladding n2 ), si introduce il parametro:
∆= (n1 2 − n2 2 ) / (2n12 )
tramite cui si possono esprimere molte delle grandezze di interesse. Per una visione raggistica del
problema, è utile ricordare la legge di Snell:
n1 sin ϑi = n2 sin ϑr
3
dove ϑi è l’angolo di incidenza del raggio, e ϑr è l’angolo del raggio rifratto. Se n1 > n2 esiste il
cosiddetto angolo limite (o critico), oltre il quale si ha riflessione totale; questo si ricava dalla legge
di Snell imponendo ϑr = π/2, da cui:
n
ϑc = arcsin 2
n1
Altro concetto importante è quello di apertura numerica; è definita come il seno dell’angolo di incidenza (in aria) del raggio che dentro al core è inclinato secondo l’angolo limite; si dimostra con
considerazioni trigonometriche (vedi es. 1) che:
NA = n1 2∆
Le curve di dispersione delle fibre vengono per convenienza normalizzate secondo i parametri:
V = ak 0 n − n = ak 0 n1 2∆
2
1
2
2
e
b=
nef2 − n22
n12 − n22
dove a è il raggio della fibra, k 0 = 2π/λ e nef = β / k 0 .
È utile ricordare che il secondo modo di una fibra compare a V ≅ 2,4 e che il numero di modi guidati
M è fornito dalla relazione: M = Int (V*V/2).
Per quando riguarda problemi relativi a bit-rate e allargamento dei segnali, si può effettuare una
stima per eccesso, sostenendo che il tempo effettivo di bit sia pari all’allargamento τ, per cui il totale risulta essere t bit = 2τ. La frequenza massima di tale sistema sarà:
B = 1 / 2τ
4
Esercizi
1) Ricavare l’espressione
∆= (n1 2 − n2 2 ) / (2n12 )
Soluzione:
dell’apertura
numerica
di
una
fibra
ottica
in
funzione
di
Applicando la legge di Snell all’interfaccia aria-fibra: sin ϑa = n1 cosϑc , da cui si rica-
va:
NA = sin θa = n1 2∆
2) Una fibra ( con nucleo grande per cui vale la teoria dei raggi ) ha indice del nucleo 1,5 e del
mantello 1,47; calcolare l’angolo critico all’interfaccia nuclo-mantello, l’apertura numerica e
l’angolo di accettazione in aria.
Soluzione: angolo critico = 78,5 gradi, NA = 0,3, accettanza = 17,37 gradi.
3) Una fibra multimodo ha diametro del nucleo 80 µm, ∆ = 1,5% e opera alla lunghezza d’onda di
0,8µm. Se n1 = 1,48, calcolare la frequenza normalizzata e il numero di modi portati (M≅V 2 /2).
Soluzione:
Ricordando la definizione di V: V=75.8, M=2873
4) Cosa succede nell’es. 3 se λ = 1.55 µm?
Soluzione:
V=41.5, M=864
5) Quanto deve essere il diametro della fibra dell’es. 3 se si vuole una operazione monomodale
(V<2,4)? Cosa succede se si riduce ∆ di un fattore 10?
Soluzione:
Dalla definizione di V: Diametro 2,53µm, diametro 8 µm.
6) Calcolare in una fibra step index multimodo di 6 Km, ∆ = 1% e n1 = 1,5, il ritardo fra modo più
veloce e più lento con tecnica raggistica. Quale bit rate massimo è possibile?
Soluzione:
Si può procedere supponendo che il raggio più veloce sia quello diretto, mentre quello più
lento viaggia con inclinazione pari all’angolo limite. Per cui: Tmin = Lmin/v g , Tmax = Lmax/ v g ,
dove v g = c/ n1 , Lmin = L, Lmax = L/sin ϑc e il ritardo è Tmax - Tmin =
Bit rate = 1/(2 τ ) = 1,7 Mb/s.
L n12
c n2
( 1 − n ) = 300 ns,
n2
1
7) Se si vuole bit rate di 100 Mb/s n1 =1,5 e ∆ = 1,5%, quanto può essere lungo il collegamento?
Soluzione:
Sfuttando il risultato dell’esercizio precedente si ricava: L = 66 m
5