Analisi matematica I (10 CFU, 100 ore)
Corso 17 (gruppo SOV-UCCZ)
)
D Periodo didattico: 30/09/2013 - 17/01/2014 (14 settimane)
D Docente: Sergio Rolando
E-mail: [email protected]
Ricevimento: ??, aula consulenze, DISMA (conviene avvisare prima)
D Esercitatore: Lucia Salari ([email protected])
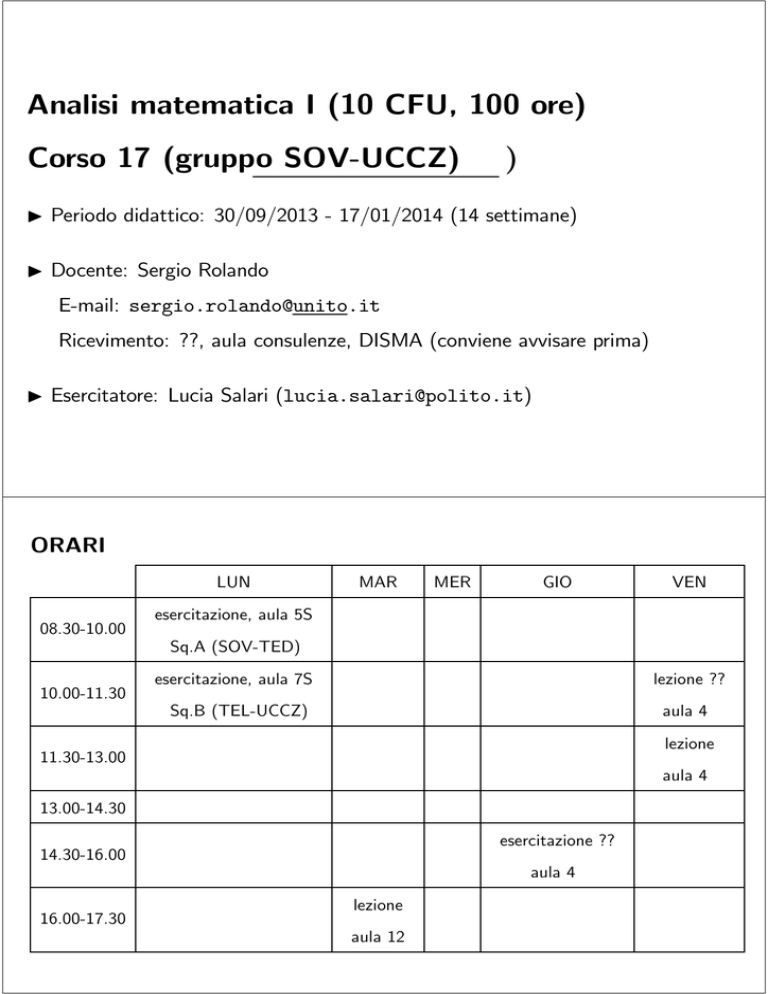
ORARI
LUN
08.30-10.00
MAR
MER
GIO
VEN
esercitazione, aula 5S
Sq.A (SOV-TED)
10.00-11.30
esercitazione, aula 7S
lezione ??
aula 4
Sq.B (TEL-UCCZ)
lezione
11.30-13.00
aula 4
13.00-14.30
esercitazione ??
14.30-16.00
16.00-17.30
aula 4
lezione
aula 12
SITO DEL CORSO
Indirizzo: segui il link su www2.dm.unito.it/paginepersonali/rolando
(sul Portale c’è anche il link diretto)
Contiene tutto ciò che può interessare sul corso: avvisi, regole d’esame, info appelli, materiale
scaricabile o consigliato, questa presentazione, ...
Avvisi urgenti e materiale d’Ateneo saranno anche sul Portale (se servisse, anche il resto).
È in aggiornamento continuo, quindi conviene consultarlo regolarmente.
PREREQUISITI DEL CORSO
Insiemi numerici e calcolo letterale. Geometria analitica. Esponenziali e logaritmi.
Trigonometria. Equazioni e disequazioni. Funzioni elementari e loro prime proprietà.
MATERIALE:
D alla propria Pagina personale del Portale della Didattica:
— Corso di accompagnamento di Matematica (videolezioni),
— e-math (materiale e-learning);
D sul sito del corso:
— link al vecchio Corso propedeutico di Matematica (materiale e-learning),
— un paio di altri file.
CONTENUTI DEL CORSO
Richiami. Simboli logici. Insiemi e operazioni sugli insiemi.
Insiemi numerici e sottoinsiemi di R; massimi, minimi, estremi superiore e inferiore.
Funzioni. Definizioni e proprietà generali. Funzioni reali di variabile reale.
Operazioni sulle funzioni.
Limiti e continuità. Limiti di funzioni e successioni; continuità. Simboli di Landau, ordine di
infinito o infinitesimo, parte principale. Proprietà delle funzioni continue su un intervallo.
Calcolo dierenziale. Derivazione e teoremi fondamentali del calcolo dierenziale (Rolle e
Lagrange). Monotonia e ottimizzazione. Regola di de L’Hôpital. Derivate di ordine superiore
e convessità. Formula di Taylor e sviluppi di McLaurin fondamentali. Applicazioni allo studio
del grafico di funzioni.
Calcolo integrale. Primitive ed integrazione indefinita. Integrazione definita nel senso di
Riemann. Teorema fondamentale del calcolo integrale. Integrali impropri.
Numeri complessi. Forma algebrica, forma trigonometrica e forma esponenziale; formule di
Eulero. Radici di numeri complessi e teorema fondamentale dell’algebra.
Equazioni dierenziali. Generalità. Equazioni del primo ordine: a variabili separabili e lineari.
Equazioni del secondo ordine: lineari a coe!cienti costanti. Problema di Cauchy.
–––––
Il dettaglio del programma svolto sarà pubblicato periodicamente sul sito, con il procedere del
corso.
COMPETENZE ATTESE
Capacità di seguire una catena di ragionamenti logici. Comprensione degli argomenti trattati
e sviluppo di abilità di calcolo. Capacità di leggere un testo tecnico.
MATERIALE DIDATTICO
Teoria:
D libro di testo adottato: Canuto-Tabacco, Analisi Matematica I, Springer, 2008
(copre tutto; gli argomenti trattati in modo sostanzialmente diverso saranno su dispensa)
D appunti
(se molto completi e integrati con eventuale altro materiale indicato in aula, coprono tutto)
D qualunque altra fonte che consenta di raggiungere gli obiettivi attesi...
Esercizi e quiz:
Quelali, Esercizi svolti di Analisi Matematica I, Clut, 2013
+ file “settimanali” di esercizi e quiz proposti, scaricabili dal sito
+ sito del corso: altri testi consigliati e altro materiale scaricabile o linkato
+ ......
MODALITA’ D’ESAME
D documento d’Ateneo, valido per tutti i corsi 16ACF in parallelo (è sul Portale e sul sito)
D sito del corso: ulteriori dettagli
DUE CONSIGLI:
D utilizzare il servizio di tutorato,
attivo dal 7/10, tutti i giorni dalle 11.30 alle 14.30, in aula 6D (terzo piano, sopra la Biblioteca)
D iscriversi al servizio SMS,
attivabile dalla propria Pagina personale del Portale.