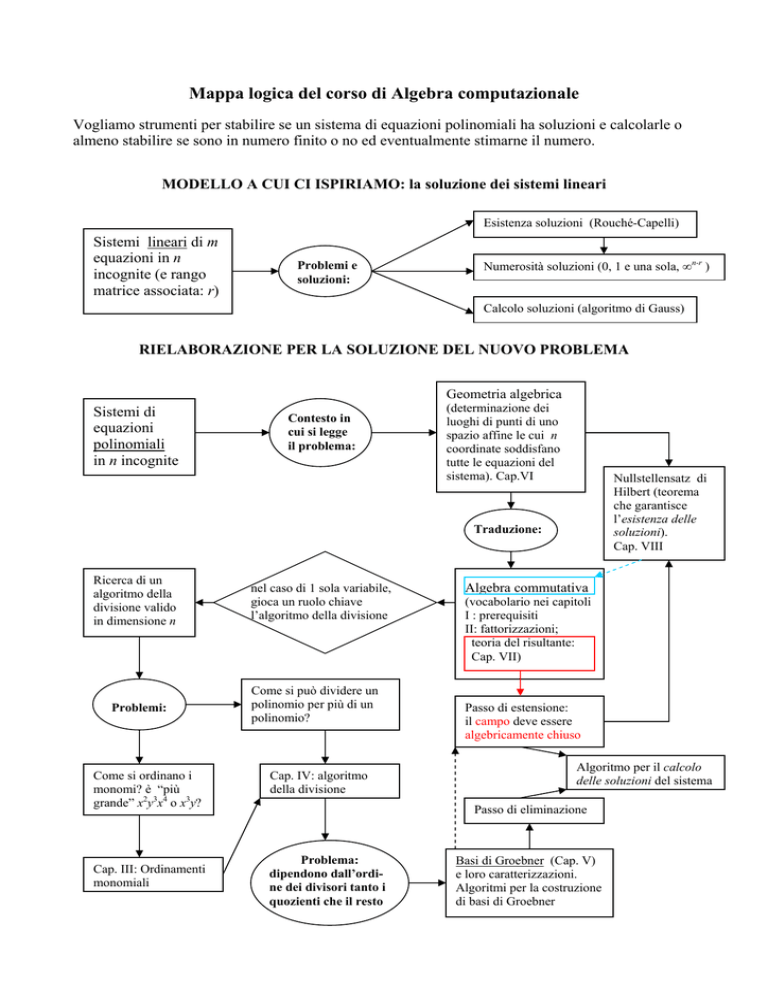
Mappa logica del corso di Algebra computazionale
Vogliamo strumenti per stabilire se un sistema di equazioni polinomiali ha soluzioni e calcolarle o
almeno stabilire se sono in numero finito o no ed eventualmente stimarne il numero.
MODELLO A CUI CI ISPIRIAMO: la soluzione dei sistemi lineari
Esistenza soluzioni (Rouché-Capelli)
Sistemi lineari di m
equazioni in n
incognite (e rango
matrice associata: r)
Problemi e
soluzioni:
Numerosità soluzioni (0, 1 e una sola, ∞n-r )
Calcolo soluzioni (algoritmo di Gauss)
RIELABORAZIONE PER LA SOLUZIONE DEL NUOVO PROBLEMA
Geometria algebrica
Sistemi di
equazioni
polinomiali
in n incognite
Contesto in
cui si legge
il problema:
(determinazione dei
luoghi di punti di uno
spazio affine le cui n
coordinate soddisfano
tutte le equazioni del
sistema). Cap.VI
Nullstellensatz di
Hilbert (teorema
che garantisce
l’esistenza delle
soluzioni).
Cap. VIII
Traduzione:
Ricerca di un
algoritmo della
divisione valido
in dimensione n
Problemi:
Come si ordinano i
monomi? è “più
grande” x2y3x4 o x3y?
Cap. III: Ordinamenti
monomiali
nel caso di 1 sola variabile,
gioca un ruolo chiave
l’algoritmo della divisione
Come si può dividere un
polinomio per più di un
polinomio?
Cap. IV: algoritmo
della divisione
Algebra commutativa
(vocabolario nei capitoli
I : prerequisiti
II: fattorizzazioni;
teoria del risultante:
Cap. VII)
Passo di estensione:
il campo deve essere
algebricamente chiuso
Algoritmo per il calcolo
delle soluzioni del sistema
Passo di eliminazione
Problema:
dipendono dall’ordine dei divisori tanto i
quozienti che il resto
Basi di Groebner (Cap. V)
e loro caratterizzazioni.
Algoritmi per la costruzione
di basi di Groebner