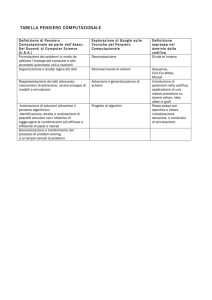
Esame di Fondamenti di Informatica II
Corso di Laurea in Ingegneria Informatica
(canale didattico di Ingegneria delle Reti e dei Servizi Informatici)
Facoltà di Ingegneria
Università degli Studi di Roma “La Sapienza” - Polo di Rieti
Prova scritta – 18 Settembre 2008
Esercizio 1
Si sviluppi in linguaggio Java un metodo ricorsivo, il cui costo computazionale in funzione della
dimensione dell’input possa essere descritto dalla seguente equazione di ricorrenza:
T(n) = T(n/2) + O(1)
Si risolva quindi l’equazione di ricorrenza (illustrare tutti i passaggi) in modo da determinare il
costo computazionale del metodo sviluppato.
Esercizio 2
Si illustri un algoritmo di ordinamento a scelta (Java o pseudocodice) tra InsertionSort,
SelectionSort e HeapSort. Si discuta dettagliatamente il costo computazionale dell’algoritmo scelto,
e lo si applichi passo passo al vettore seguente:
{ 2, 10, 12, 11, 3, 7, 1, 52, 27, 9, 3 }
Esercizio 3
Si illustri una rappresentazione a scelta per grafi non diretti, tra liste di adiacenza e matrice di
adiacenza. In particolare, per la rappresentazione scelta, si determini il costo computazionale delle
seguenti operazioni (motivare le risposte): archiIncidenti (v), aggiungiVertice (v), aggiungiArco
(x, y), sonoAdiacenti (u, v). Si sviluppi quindi un metodo Java che, dato in input un grafo nella
rappresentazione scelta, restituisca true se ogni nodo ha lo stesso grado, false altrimenti.
Determinare infine il costo computazionale del metodo sviluppato.
pag. 1/2
Esercizio 4
Si definiscano i concetti di delimitazione superiore (upper bound) e delimitazione inferiore (lower
bound) alla complessità di un problema. Si forniscano quindi un upper bound ed un lower bound
per il problema dell’individuazione di un minimo albero ricoprente in un grafo non diretto
(motivare brevemente le risposte).
Esercizio 5
Si illustri dettagliatamente (implementazione Java o pseudocodice) l’algoritmo di Dijkstra per il
problema dei cammini minimi in un grafo. Se ne discutano le prestazioni asintotiche e lo si applichi
al grafo seguente, a partire dal nodo S:
1
A
2
3
B
C
2
10
S
2
E
4
F
5
D
G
2
pag. 2/2