Lezione 3
Applicazioni della Legge di Gauss
r
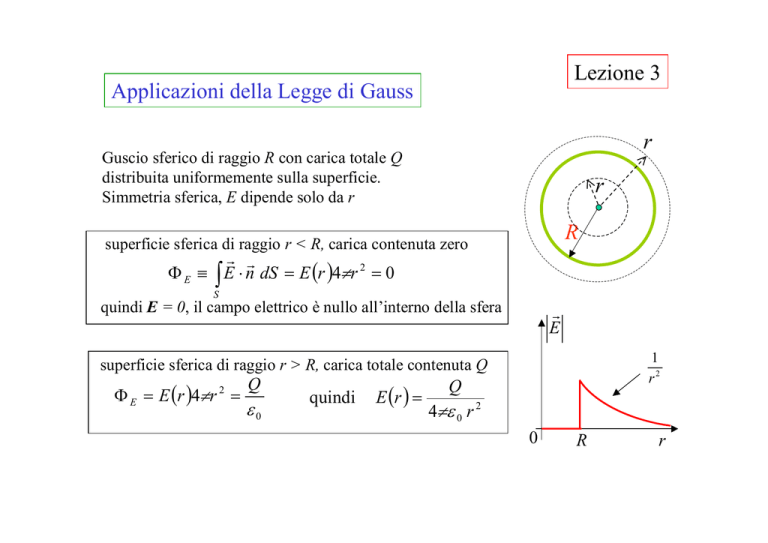
Guscio sferico di raggio R con carica totale Q
distribuita uniformemente sulla superficie.
Simmetria sferica, E dipende solo da r
r
R
Φ E ≡ ∫ E ⋅ n dS = E (r )4πr 2 = 0
superficie sferica di raggio r < R, carica contenuta zero
S
quindi E = 0, il campo elettrico è nullo all’interno della sfera
E
1
r2
superficie sferica di raggio r > R, carica totale contenuta Q
Φ E = E (r )4πr 2 =
Q
ε0
quindi
E (r ) =
Q
4πε 0 r 2
0
R
r
Notiamo che il campo elettrico all’esterno della sfera è uguale a quello generato da una carica
puntiforme e questo varrà per qualsiasi corpo con carica distribuita a simmetria sferica.
Per raggio r > R, il potenziale (per quanto detto) deve
essere uguale a quello di una carica puntiforme:
V (r ) =
Q
4πε 0 r
in particolar e V (R ) =
Potenziale elettrico:
Q
4πε 0 R
Per raggio r < R, il potenziale si calcola dalla definizione:
∆ V = (V ( B ) − V ( A) ) = − ∫ E ⋅ d s
B
A
V (r )
considerando un percorso da R (estremo A)
a r (estremo B) verso l’interno della sfera
(r < R), il campo è nullo quindi:
V ( r ) = V ( R ) − ∫ E ⋅ ds
1
r
V ( R)
r
R
V (r) = V ( R ) =
Q
4πε 0 R
= costante
0
R
r
Energia elettrostatica
Lavoro esterno per creare una configurazione di cariche elettriche.
Esempio: lavoro per portare la carica totale Q sul guscio sferico, inizialmente scarico
Per portare sul guscio una carica infinitesima dq :
dL = V ( q) dq ;
V ( q) =
Aggiungendo continuamente dq , sulla sfera si parte da q = 0 e si continua fino
ad avere la carica Q (sfera completamente carica); il lavoro totale è
Energia elettrostatica del guscio carico
Eelett .
1 Q2
=
2 4πε 0 R
1
Q
Q
1
Q
1 2
=
L = ∫ dL =∫ V (q) dq =
q
dq
q
∫
4πε 0 R 0
4πε 0 R 2
0
0
Q
0
q
4πε 0 R
1 Q2
=
2 4πε 0 R
V(q)
V
Eelett .
dq
[Eelett ] = J (Joule)
0
q
Q
Piano esteso caricato uniformemente con densità di carica σ
σ
r
E
σ=
∆Q
∆S
S
S
ΦE =
∫ E ⋅ n dS
= 0 + E (r )
r
n
∫ E ⋅ n dS
=
∫ E ⋅ n dS =
+
∫ dS = E (r ) ⋅ 2S
Sup laterale
Sup basi
Sup basi
S
r
n
r
n
C
m2
Data la simmetria planare il campo elettrico è diretto
perpendicolarmente al piano e può dipendere solo dalla
distanza r dal piano. Su un cilindro di base S che viene
tagliato dal piano:
Sup . cilindro
r
n
[σ ] =
carica per unità di superficie
Per la legge di Gauss: Φ E =
quindi risulta:
E=
Qcont .
ε0
=
σ ⋅S
ε0
σ
= cost.
2ε 0
e il campo elettrico non dipende dalla distanza dal piano
Conduttori:
Corpi in cui vi sono cariche elettriche libere di
muoversi (es. nei metalli gli elettroni)
1) all’interno il campo elettrico è sempre nullo, E = 0;
2) vicino all’esterno il campo elettrico è sempre
perpendicolare alla superficie;
3) Su un conduttore carico, le cariche si distribuiscono solo
sulla superficie;
4) Induzione elettrostatica: su un conduttore (neutro) in
un campo elettrico esterno si induce una distribuzione di
cariche (positive e negative) che produce al suo interno un
campo elettrico uguale e opposto a quello esterno, in modo
che la somma sia zero.
Conduttori in equilibrio:
E = 0 all’equilibrio
Eest .
Sup
quindi Q = 0 all’interno
Eindotto
ε0
Eest . + Eindotto = 0
Sup .
Qcont.
∫ E ⋅ n dS = ∫ 0 dS = 0 =
ΦE =
Eest .
Schermo elettrostatico
r
E=0
Corpo carico circondato da guscio conduttore:
si formano cariche indotte, di segno diverso
sulle due superfici del guscio, per equilibrare il
campo del corpo interno, e annullare il campo
all’interno del materiale del guscio.
r
E≠0
Il campo prodotto all'esterno dipende
dalla distribuzione di cariche alla
superficie dello schermo conduttore
Le forze prodotte da un campo
esterno agiscono sullo schermo ma
non sulle cariche interne.
La distribuzione delle cariche interne non muta il campo esterno; viceversa, il
campo esterno non influenza le cariche interne (schermo di Faraday, descritto già da
Benjamin Franklin nel 1755)
Campo elettrico vicino a un conduttore carico
r
E
Legge di Gauss su un cilindretto tagliato dalla
superficie del conduttore carico; all’interno E = 0
ΦE =
= E (r )
∫ dS = E (r ) ⋅ S
S
Sup base
ma Φ E =
Qcont .
ε0
=
σ ⋅S
ε0
quindi
E=
σ
ε0
σ
Dato che E = 0 all’interno, V è costante,
V all’interno = V sulla superficie
0 = Ex, y,z
∂V
=−
∂x, y, z
Il conduttore è equipotenziale
Potenziale di un conduttore carico
V = cost
Capacità C :
rapporto tra carica e potenziale
Per una sfera conduttrice carica di
raggio R (o per un guscio carico)
V=
Q
4πε 0 R
Q
Q
C = = 1 Q = 4πε 0 R
V
4πε R
0
1 Farad =
1 Coulomb
1 Volt
Q
C
= =F
V
V
[C ] =
unità di misura
Q
C=
V
(dipende dalla geometria dei
corpi conduttori carichi)
Si usano i sottomultipli perchè
l’unità di misura naturale risulta
troppo grande: µF, nF, pF
Esempio:
capacità della Terra (raggio R ≈ 6300 km)
C = 4πε 0 R ≈ 7 ⋅ 10 −4 F
due gusci metallici concentrici di raggi
R1 e R2 , con cariche +Q e -Q
Condensatore sferico
campo elettrico:
E = 0 per r < R1 , r > R2
1 Q
per R1 < r < R2
E (r ) =
2
4πε 0 r
EE(r)
(r )
+Q r
−Q
R2
R2
capacità: C =
Osserviamo che se R 2 → ∞ ,
Q
Q
≡
=
V
∆V
1
Q
Q
=
dr
4πε 0
r2
4πε 0
Q
Q
4 πε 0
C → C 1 = 4πε 0 R1
1
1
−
R1 R 2
= 4πε 0
R1
= − ∫ E ( r ) dr = − ∫
R1
R2
∆ V = V ( R1 ) − V ( R 2 ) =
R1
differenza di potenziale
1
1
−
R1 R 2
R1 R 2
R 2 − R1
capacità della sfera isolata
Condensatore piano
+σ
d
−σ
due piani metallici di superficie S, affacciati
a distanza d, con densità di carica +σ e -σ
campo elettrico: all’esterno E = 0
S
tra le armature del condensatore
E=
r
E≠0
σ
σ
σ
+
=
2ε 0 2ε 0 ε 0
E da cariche +
E da cariche -
σd
∆V = E ⋅ d =
ε0
Q Q
S
σS
C= ≡
=
= ε0
V ∆V σ d / ε 0
d
differenza di potenziale:
(con E costante)
capacità:
r
E=0
∆V
r
E=0
C = ε0
Superficie
distanza
Condensatore: immagazzinamento di cariche elettriche
3C
S
a
b
c
d
C = ε0
S
d
Nel calcolo della capacità del condensatore
occorre sommare la superficie S delle armature
di polarità opposta tra loro affacciate; in questo
caso la capacità totale vale 3C
Energia elettrostatica del condensatore piano
uguale al lavoro necessario per portare la carica q del condensatore da 0 a Q
Per spostare la carica infinitesima dq
dall’armatura negativa a quella positiva: dL = ∆V (q) dq;
Q
Energia del condensatore
1 Q2 1
1
2
EC =
= C V = QV
2 C 2
2
Q
d
d 1 2
L = ∫ dL =
q
dq
q
=
∫
S
S
ε
ε
2
0
0
0
0
Q
Il processo di carica parte da q = 0
e continua fino a raggiungere Q; il
lavoro totale è:
∆V (q) = E(q) ⋅ d =
0
σ d qd
=
ε0 ε0 S
d 1 2 1 Q2
=
Q =
ε0 S 2
2 C
Q2
C2 C2
[EC ] =
=
=
= CV = J (Joule)
C
F C/V
Densità di energia del campo elettrico
d
2d
condensatore piano a
distanza d con carica Q
condensatore piano a
distanza 2d con carica Q
1 Q2 1 2 d
= Q
E1 =
2 C1 2
ε0S
C1
C2
1 Q 2 1 2 2d
E2 =
= Q
= 2 E1
ε0S
2 C2 2
L’energia elettrostatica accumulata dal
condensatore è nella forma di una
energia associata al campo elettrico
presente nel volume tra le armature
Ogni campo elettrico possiede una energia (per
unità di volume) data dalla formula precedente;
la formazione di un campo elettrostatico nello
spazio richiede questa spesa energetica
1
1 S
1
1
2
EC = C V 2 = ε 0 (Ed ) = ε 0 E 2 S d = ε 0 E 2 ⋅Vol
2
2 d
2
2
EC
1
Def.: densità di energia del campo elettrico
2
E
u
=
ε
=
E
0
= energia per unità di volume (J/m3)
Vol
2
L’energia elettrostatica è proporzionale al volume compreso tra le armature! Infatti:












