Il problema delle correnti a vuoto nel trasformatore trifase è

Correnti a vuoto nel trasformatore trifase
Il problema delle correnti a vuoto nel trasformatore trifase è importante
in quanto, a seconda dei collegamenti delle fasi, si avrà o meno la deformazione dei flussi o della corrente magnetizzante. Considereremo per
semplicità il caso di un trasformatore con nucleo a colonne, trascurando
la limitata differenza delle correnti magnetizzanti delle colonne laterali
rispetto a quella centrale.
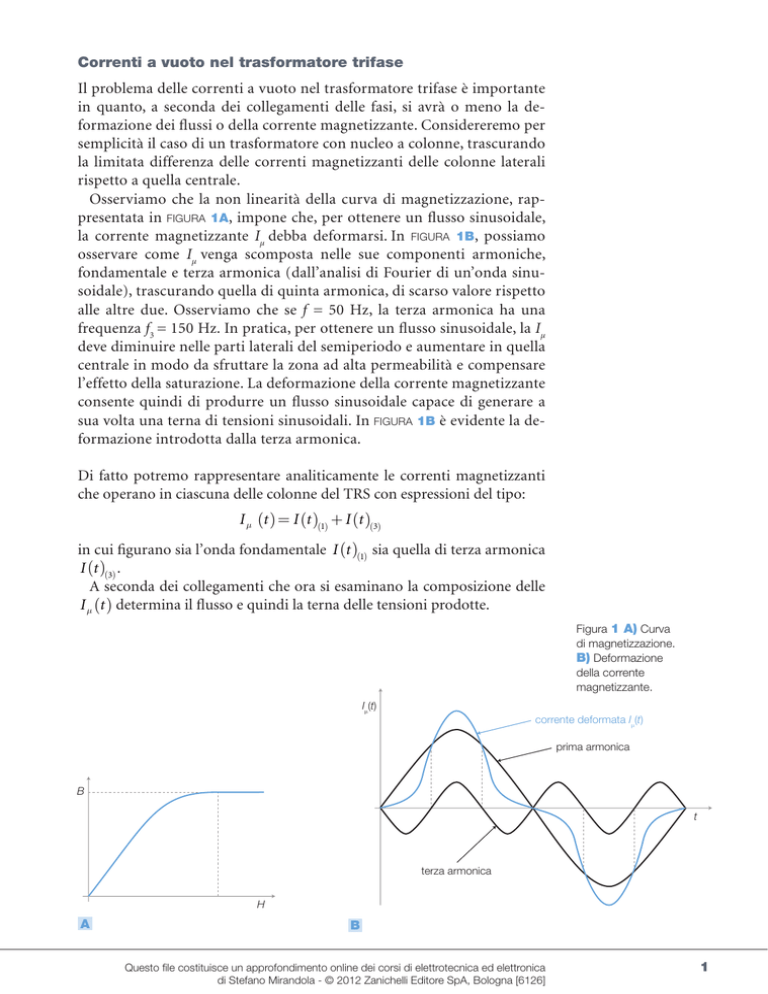
Osserviamo che la non linearità della curva di magnetizzazione, rappresentata in FIGURA 1A, impone che, per ottenere un flusso sinusoidale,
la corrente magnetizzante Iµ debba deformarsi. In FIGURA 1B, possiamo
osservare come Iµ venga scomposta nelle sue componenti armoniche,
fondamentale e terza armonica (dall’analisi di Fourier di un’onda sinusoidale), trascurando quella di quinta armonica, di scarso valore rispetto
alle altre due. Osserviamo che se f = 50 Hz, la terza armonica ha una
frequenza f3 = 150 Hz. In pratica, per ottenere un flusso sinusoidale, la Iµ
deve diminuire nelle parti laterali del semiperiodo e aumentare in quella
centrale in modo da sfruttare la zona ad alta permeabilità e compensare
l’effetto della saturazione. La deformazione della corrente magnetizzante
consente quindi di produrre un flusso sinusoidale capace di generare a
sua volta una terna di tensioni sinusoidali. In FIGURA 1B è evidente la deformazione introdotta dalla terza armonica.
Di fatto potremo rappresentare analiticamente le correnti magnetizzanti
che operano in ciascuna delle colonne del TRS con espressioni del tipo:
I µ (t ) = I (t )(1) + I (t )(3)
B
in cui figurano sia l’onda fondamentale I (t )(1) sia quella di terza armonica
I (t )(3) .
A seconda dei collegamenti che ora si esaminano la composizione delle
I µ (t ) determina il flusso e quindi la terna delle tensioni prodotte.
H
Iµ(t)
Figura 1 A) Curva
di magnetizzazione.
B) Deformazione
della corrente
magnetizzante.
corrente deformata Iµ(t)
prima armonica
B
t
terza armonica
H
A
Iµ
B
Questo file costituisce un approfondimento online dei corsi di elettrotecnica ed elettronica
corrente
deformata
Iµ(t) Zanichelli Editore SpA, Bologna [6126]
di Stefano
Mirandola
- © 2012
1
Collegamento Y/y con neutro al primario
In questo caso nel centro stella si sommano le tre correnti magnetizzanti: si
osserva che le componenti di prima armonica sono sfasate di 120° tra loro
e formano una terna sinusoidale simmetrica ed equilibrata con somma vettoriale uguale a zero, mentre le correnti di terza armonica sono in fase tra
di loro, come si vede in FIGURA 2.
Nel neutro circola allora una corrente di frequenza 150 Hz data dalla somma delle tre terze armoniche delle tre correnti magnetizzanti.
In questo modo le terze armoniche circolano liberamente e modulano
la Iμ in ciascuna colonna, consentendo la produzione di flussi sinusoidali
che, grazie alla compensazione delle non-linearità, sono privi di deformazioni.
FIGURA 2 Composizione
delle correnti
magnetizzanti.
Iµ
corrente magnetizzante
nella prima colonna
60°
180°
120°
300°
240°
360°
t
Iµ
corrente magnetizzante
nella seconda colonna
60°
180°
120°
300°
240°
360°
t
Iµ
corrente magnetizzante
nella terza colonna
60°
180°
120°
300°
240°
Questo file costituisce un approfondimento online dei corsi di elettrotecnica ed elettronica
di Stefano Mirandola - © 2012 Zanichelli Editore SpA, Bologna [6126]
360°
t
2
Collegamento Y/y senza neutro
In questo caso, nel centro stella primario deve avvenire la somma delle correnti magnetizzanti, sia per quanto riguarda le componenti fondamentali
sia per quelle di terza armonica. Per quanto riguarda le prime, la loro somma è sicuramente uguale a zero, formando una terna simmetrica ed equilibrata. Per le componenti di terza armonica, essendo in fase tra loro, perché
la somma sia zero debbono essere tutte nulle. La corrente magnetizzante
sarà allora sinusoidale per cui il flusso si deforma, secondo il modello di
FIGURA 3. In modo analogo si deformano le tensioni indotte stellate secondaria e di reazione primaria. Le tensioni di linea, essendo generate dalla
differenza vettoriale di quelle concatenate, non si deformano in quanto le
rispettive terze armoniche vengono a trovarsi in opposizione di fase, annullandosi a vicenda.
flusso totale deformato
Φ(t)
prima armonica
ωt
terza armonica
FIGURA 3 Deformazione del flusso.
Collegamento D/y con neutro al secondario
In questo caso, dal momento che la maglia a stella del primario consente la
circolazione delle correnti di terza armonica, potendosi quindi deformare
la corrente magnetizzante, si mantiene la sinusoidalità del flusso, anche nel
secondario si avranno le stesse condizioni del caso precedente.
Dal punto di vista dei problemi dovuti alla terza armonica, questa soluzione è la migliore in quanto non si hanno sostanziali deformazioni nel
flusso e quindi nei valori delle tensioni.
Cenni sul comportamento dei TRS trifase ai carichi squilibrati
In generale il migliore funzionamento di un TRS trifase avviene quando le
tre correnti secondarie sono poco differenti e il carico che viene alimentato
è lo stesso per tutte e tre le fasi, anche se ottenuto collegando utilizzatori
monofase tra il neutro e ciascuna fase secondaria (corretta ripartizione dei
carichi).
Taluni collegamenti, tuttavia, consentono di ottenere un accettabile funzionamento anche con carichi squilibrati. Esaminiamo quelli di più frequente uso.
Questo file costituisce un approfondimento online dei corsi di elettrotecnica ed elettronica
di Stefano Mirandola - © 2012 Zanichelli Editore SpA, Bologna [6126]
3
Collegamento Y/y con e senza neutro al primario e al secondario
Supponiamo di collegare l’impedenza ZTn tra la fase T2 e il neutro n2 del secondario: la presenza di ZTn determina la circolazione di una corrente IT n che
2 2
richiama una corrente di reazione I'T n tra la corrispondente fase primaria e
1 1
in neutro, come indicato in FIGURA 4. La corrente di reazione primaria circola
nel conduttore di neutro e non va a interessare le altre fasi, non dando luogo
a variazioni di flusso e quindi a variazioni delle forze elettromotrici indotte
nelle fasi.
Analogamente la corrente di carico va a richiudersi attraverso il neutro al
secondario, senza determinare perturbazioni nelle altre due fasi.
Il sistema dei flussi quindi non subisce variazioni e la macchina continua a
funzionare senza variazioni di tensione in uscita. Questa soluzione è adatta
ad alimentare carichi squilibrati mantenendo costanti le tensioni di linea.
R1
S1
T1
n1
R1
R1
R1
R1
S1
T1
R1
S1
T1
n1
R1
R1
R1
R1
S1
T1
I'T1 n1
I'T1 n1
I'T1
I'T1
I'2T1
I'2T1
2
2
I'T1
I'T1
IT2 n2
IT2 n2
IT2 n2
IT2 n2
ZTN
ZTN
IT2 n2
IT2 n2
ZTN
ZTN
R2
S2
T2
n2
R2
S2
T2
n2
Figura 4 Carico squilibrato su collegamento Y/y
R2 neutro.
S2
T2
n2
R2
S2
con
R2
S2
T2
n2
R2
S2
ZTN
ZTN
T2
n2
T2
n2
Se si elimina il neutro al primario, come in FIGURA 5, al primario viene richiamata una corrente di reazione I'T che, non essendo più presente il neu1
tro, deve richiudersi attraverso le altre due fasi, indicativamente in ognuna
di esse circolerà una corrente I'T /2.
1
Questa situazione produce l’effetto di aumentare la magnetizzazione del
nucleo, con il risultato di squilibrare le tensioni indotte primarie e secondarie, determinando un malfunzionamento della macchina e degli altri carichi (simmetrici) eventualmente presenti al secondario, che si trovano a
funzionare con una tensione maggiore di quella nominale.
Questo collegamento non è, quindi, adatto ad alimentare carichi squilibrati.
n1
R1
n1
R1
I'T1 n1
I'T1 n1
R1
I'T1
R1
R1
I'T1
I'2T1
I'2T1
2
2
R1
S1
T1
R1
S1
T1
I'T1
I'T1
IT2 n2
I
R1
IT2 n2
I
ZTTNn
ZTTNn
ZTN
ZTN
2 2
IT2 n2
I
ZTTNn
2 2
2 2
ZTN
n2
R2
S2
T2
n2
n2
R2
S2
T2
n2
Figura 5 Carico squilibrato su collegamento Y/y
S2al primario.
T2
n2
2
senzaRneutro
R2
S2
T2
n2
Questo file costituisce un approfondimento online dei corsi di elettrotecnica ed elettronica
di Stefano Mirandola - © 2012 Zanichelli Editore SpA, Bologna [6126]
4
R1
S1
T1
n1
R1
R1
R1
R1
R1 alSsecondario
T1
n1
R1
R1
R1
1
Collegamento D/y con neutro
I'T
I'T
I'T richiaIn questo caso, (FIGURA 6), la corrente di reazione nella fase primaria
2 I'T 2 I'T
I'
n squilibrio si richiude attraverso
I'T
mata dalla corrente secondaria del caricoTdi
2
2
I'
la linea e non va a interessare le altre fasi. SiT ndice che in queste condizioni
il TRS trifase viene a comportarsi come un gruppo di tre TRS monofase
indipendenti.
Questo tipo di collegamento viene molto
IT n usato nelle cabine per l’alimenIT n
tazione di carichi a bassa tensione equilibrati
e
squilibrati.
I
I
1
S1
R1
T1
S1
T1
1
1
1
1 1
1
1
1 1
2 2
ZTN
ZTN
T2 n2
ZTN
R2
S2
T2
n2
2
2
ZTN
T2 n2
ZTN
R2
S2
T2
13.2
Dati caratteristici
nei
trasformatori
trifase
R
S
T
n
R
S
T
2
IT2 n2
2 2
2
2
2
ZTN
n2
2
IT2 n2
R2
n2
Le formule che consentono di calcolare i dati caratteristici tengono conto
del fatto che si sta operando in un sistema trifase, in cui il TRS si comporta
come un insieme di tre monofase collegati nei modi visti nel paragrafo
precedente; per cui abbiamo:
S2
T2
n2
R2
S2
T2
FIGURA
6 Carico
n2
squilibrato su collegamento
D/y con neutro al secondario.
An = 3 ⋅ V1n ⋅ I1n
•potenza apparente al primario:
•potenza attiva resa al secondario: P2n = 3 ⋅ V2n ⋅ I 2n ⋅ cosϕ2 •potenza persa per effetto Joule negli avvolgimenti:
PJoule = 3 ⋅ R1 ⋅ I 12n + 3 ⋅ R2 ⋅ I 22n
oppure:
oppure:
•perdite nel ferro:
PJoule = 3 ⋅ Re' ⋅ I 12 = 3 ⋅ R'' ⋅ I 22
2
 I 
2

PJoule = Pcc ⋅ 
 I 2n 
V
PFe = P0 ⋅ 1
 V
2
2

V 
 = P0 ⋅ 20 
 V 

1n 
2n
•caduta di tensione industriale: ∆V2 = 3 ⋅ I 2 ⋅( R2'' ⋅ cosϕ2 + X e'' ⋅ senϕ2 )
3 ⋅ E1
•resistenza trasversale: R0 =
P0
R
•reattanza trasversale: X µ = 0
tgϕ0
•resistenza equivalente al secondario: Re'' =
Pcc
3 ⋅ I 22n
•reattanza equivalente secondaria: X e'' = X e'' ⋅ tgϕcc
P2n
•rendimento: η =
P2n + PJoule + PFe + Padd
L’uso delle formule indicate presuppone la conoscenza dei dati di targa del
trasformatore trifase, del tutto identici a quello monofase, con la sola aggiunta del tipo di collegamento e del gruppo di appartenenza.
Questo file costituisce un approfondimento online dei corsi di elettrotecnica ed elettronica
di Stefano Mirandola - © 2012 Zanichelli Editore SpA, Bologna [6126]
5