FORMULE PER L`IPERBOLE

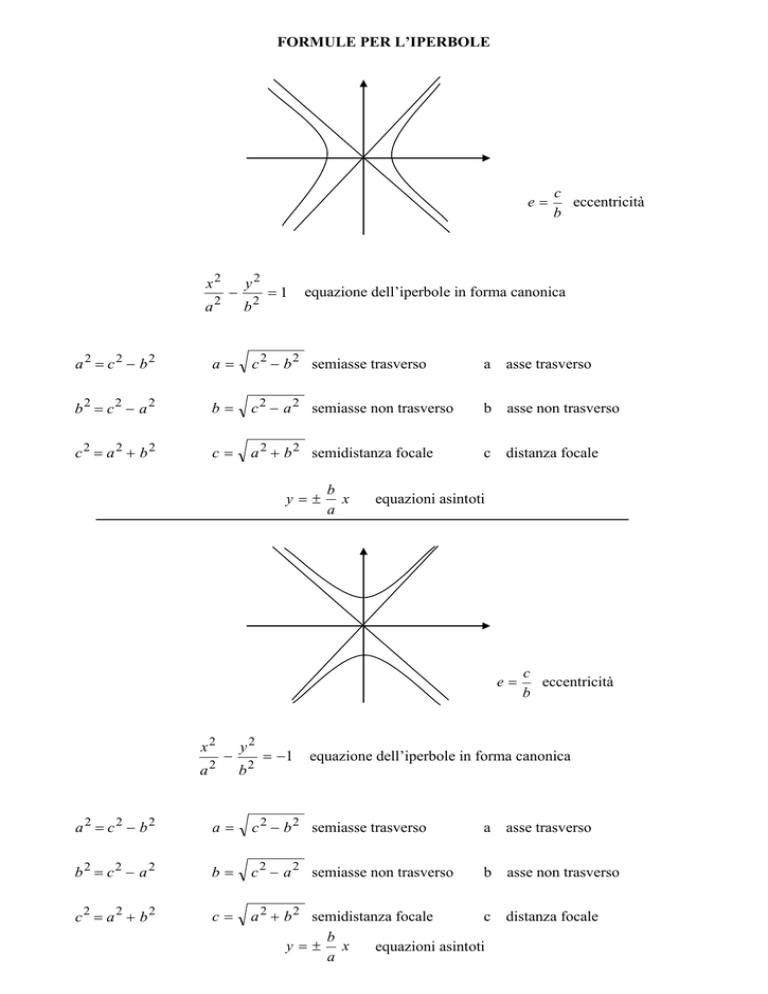
FORMULE PER L’IPERBOLE
e
x2
a2

y2
b2
1
c
eccentricità
b
equazione dell’iperbole in forma canonica
a2  c2  b2
a
c 2  b 2 semiasse trasverso
a asse trasverso
b2  c2  a2
b
c 2  a 2 semiasse non trasverso
b
c2  a2  b2
c
a 2  b 2 semidistanza focale
c distanza focale
y
b
x
a
asse non trasverso
equazioni asintoti
e
x2
a2

y2
b2
 1
c
eccentricità
b
equazione dell’iperbole in forma canonica
a2  c2  b2
a
c 2  b 2 semiasse trasverso
a asse trasverso
b2  c2  a2
b
c 2  a 2 semiasse non trasverso
b
c2  a2  b2
c
a 2  b 2 semidistanza focale
c distanza focale
b
y x
equazioni asintoti
a
asse non trasverso
IPERBOLE EQUILATERA RIFERITA AGLI ASSI
x2  y2  a2
c2  2 a2
ca 2
semidistanza focale
yx
equazioni degli asintoti
e
x2  y2   a2
c2  2 a2
ca 2
semidistanza focale
yx
equazioni degli asintoti
c
eccentricità
b
IPERBOLE EQUILATERA RIFERITA AGLI ASINTOTI
xy  k
c2  4 k
c 2
k
con k  0
semidistanza focale
y0
x0
xy  k
c2  4 k
c 2
k
equazioni degli asintoti
con k  0
semidistanza focale
y0
x0
equazioni degli asintoti
FUNZIONE OMOGRAFICA
O’
y
y
a
c
x
ax  b
cx  d
asintoto orizzontale
d
c
asintoto verticale
 d a
O'   ; 
 c c 
centro della funzione omografica