Introduzione ai convertitori Digitali

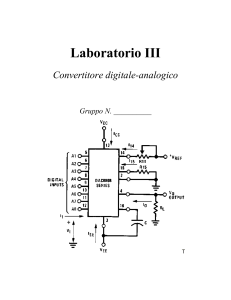
Introduzione ai convertitori Digitali-Analogici (DAC)
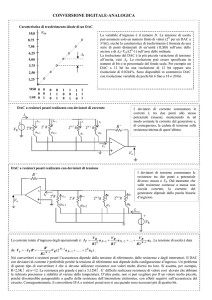
Consideriamo il circuito sommatore rappresentato nella figura 1, dove si assumono ideali tutti i
componenti (amplificatore operazionale, deviatori Si, resistenze R).
- VR
S2
D2
D1
R
S0
S1
D0
2 R
4R
VO
RF=R/2
Figura 1
La posizione di ciascun deviatore è controllata dal valore 0 oppure 1 di un bit Di. Al valore 0
corrisponde la condizione di deviatore a massa, al valore 1 la condizione di deviatore collegato a –
VR.
Chiamiamo D2, D1, D0 i bit di controllo, rispettivamente, dei deviatori S2, S1, S0.
Consideriamo la parola digitale costituita dall’insieme dei tre bit Di : sappiamo che può assumere
23=8 configurazioni distinte NK (K=0,…,7), come si vede dalla tabella 1, individuabili con le cifre
decimali N da 0 a 7 codificate in binario.
Tabella 1
Configurazione
N0
N1
N2
N3
N4
N5
N6
N7
Numero N
0
1
2
3
4
5
6
7
D2
0
0
0
0
1
1
1
1
D1
0
0
1
1
0
0
1
1
D0
0
1
0
1
0
1
0
1
Aggiungiamo alla tabella una ulteriore colonna Vo, dove riportiamo (tabella 2) i valori dell’uscita in
corrispondenza a ciascuna delle possibili configurazioni dei deviatori, assumendo, nel calcolo,
VR=10V (suggerimento: far calcolare dagli studenti i valori di Vo).
Tabella 2
Configurazione
N0
N1
N2
N3
N4
N5
N6
N7
Numero N
0
1
2
3
4
5
6
7
D2
0
0
0
0
1
1
1
1
D1
0
0
1
1
0
0
1
1
D0
0
1
0
1
0
1
0
1
Vo (V)
0
1.25
2.5
3.75
5
6.25
7.5
8.75
Esercizio 1
Ricavare l’espressione letterale generale di Vo in funzione del valore Di dei singoli bit e della
tensione di riferimento VR.
Sovrapponendo gli effetti dei singoli rami si ottiene facilmente
2
Vo  VR ( D2  D1  D0 )  VR ( 2(3i ) Di )
1
2
1
4
1
8
(1)
i 0
In generale, con n bit
n1
Vo  VR ( 2 ( ni ) Di )
(2)
i 0
Si noti che, facendo corrispondere a ciascuna parola D2D1D0 il valore decimale NK equivalente
mostrato in tabella [ovvero moltiplicando e dividendo per 23 il 2° membro della (1)], possiamo
anche scrivere che
Vo 
VR 2
(2 D2  21 D1  20 D0 )  VR
3
2
NK
8
Commento: il circuito sommatore in esame converte una parola digitale di 3 bit (che chiameremo
codice binario in ingresso) in una tensione proporzionale al valore decimale NK corrispondente.
Il circuito realizza quindi una conversione digitale-analogica e per questo viene chiamato DAC
(Digital-to-Analog Converter)
Esercizio 2
Rappresentare in un piano cartesiano Vo in funzione del codice di ingresso. (Questa
rappresentazione è detta anche”caratteristica di trasferimento del DAC”).
Caratteristica di trasferimento di un DAC a 3 bit
con VFS=10V
10,00
8,75
Vo (V)
7,50
6,25
5,00
3,75
2,50
1,25
0,00
000
001
010
011
100
101
110
111
Codice di ingresso
Osservazione: in sostanza il sommatore presenta in uscita uno tra i 2n (n= numero dei bit nella
parola digitale, 3 in questo esempio) valori che si ottengono dalla suddivisione in 2n parti uguali
della tensione VR=10 V. VR corrisponde anche alla tensione di fondo scala VFS del DAC.
Notiamo che in questo caso la più piccola variazione di Vo, pari all’incremento dell’uscita da un
codice al successivo (incremento che prende il nome di “risoluzione” del DAC), vale 1.25 V , cioè
10/8 V.
Esercizio 3
Trovare l’espressione letterale generale della risoluzione di un DAC con tensione di fondo scala VFS
e codice di ingresso a n bit
Risoluzione = VFS/2n
Osservazione: la risoluzione corrisponde al peso del bit meno significativo (LSB) nell’espressione
generale 2). [ Per n=3 si vede dalla 1) che il peso di D0 vale 2-3=1/8]
Esercizio 4
Calcolare la risoluzione di un DAC a 10 bit con VFS=5 V
Risoluzione = 5/210 V=5/1024 V 5 mV.
Abbiamo sin qui considerato ideali tanto l’amplificatore operazionale quanto i deviatori;
esaminiamo ora gli effetti delle non idealità.
L’amplificatore operazionale reale presenta un offset di tensione eo che si riflette su Vo in modo
indipendente dal codice di ingresso, come si evince dal seguente esercizio.
Esercizio 5
Calcolare la tensione Verr in uscita dal DAC della figura 1, dovuto a una tensione di offset
eo=10mV.
Osserviamo che, utilizzando la sovrapposizione degli effetti tra i generatori eo e VR, ci si rende
immediatamente conto che, indipendentemente dal valore del bit di controllo, i resistori R, 2R, 4R
sono tutti a massa quando è presente solo eo.
Dobbiamo quindi trovare la tensione di uscita della configurazione non invertente mostrata nella
figura 2, dove Req è il parallelo tra R, 2R e 4R.
R/2
Req
Verr
eo
Figura 2
Si trova che Req Re quindi Verr= (1+.5R/.57R) eo 19 mV.
In questo caso l'errore è piccolo rispetto all'LSB, ma il suo peso cresce al crescere di n.

Tenendo conto dell'offset, l'espressione generale 2) diventa:
ni
Vo  VR ( 2 ( ni ) Di )  Verr (eo )
(3)
i 0
Domanda
Che effetto ha questo errore sulla caratteristica di trasferimento di un DAC?
Risposta
La caratteristica viene traslata rigidamente di una quantità pari a Verr.
Osservazione
E’ noto che l’effetto dell’offset di tensione può essere portato a 0 in uscita agendo su opportuni
trimmer, ma la regolazione dipende dalle condizioni operative (temperatura, alimentazioni, età del
componente) e quindi deve essere periodicamente rifatta.
Domanda
Nell’esempio della figura 1) le correnti di polarizzazione introducono errori su Vo?
Risposta
Introduce errori la corrente di polarizzazione del morsetto negativo.
Assumendo che anche i deviatori Si siano reali, dobbiamo tener conto che si comportano come
resistenze ri in serie al ramo in cui sono inseriti, cambiando così il peso del relativo bit, come si
ricava dall’esercizio seguente.
Esercizio 6
Calcolo del peso effettivo di ciascun bit Di con Si reale
R/2
i=0,...,n-1
ri
2n-1-iR
-VR
Vo
Figura 3
R
Vo   r 2n21i R (VR )  VR
i
R
2 ri  2n i R
 VR 2 ( ni ) ( 12 ( n11i ) ri )  VR 2 ( ni ) (1  2 ( n1i ) Rri )
R
Commento
Le ri determinano una non linearità nella caratteristica di trasferimento, variando l’incremento
dell’uscita da un codice al successivo, incremento che differisce così dal valore ideale di 1 LSB.
Domanda
Cosa succede se le resistenze R non rispettano rigorosamente i rapporti indicati nella figura 1)?
Risposta
Si hanno effetti analoghi ai precedenti di non linearità sull’uscita, oltre a errori di guadagno (cambia
la pendenza della caratteristica di trasferimento).
Nei DAC reali può capitare che un deviatore si guasti, rimanendo sempre collegato a VR o a massa,
indipendentemente dal valore che assume il suo bit di controllo. Esaminiamo gli effetti di questo
malfunzionamento nel seguente esercizio.
(4)
Esercizio 7
Si ricalcolino i valori di Vo nella tabella 1) con S1 sempre a massa (caso a) oppure sempre a VR
(caso b) e si disegnino le caratteristiche di trasferimento normalizzate. Commentare i risultati
Caratteristica di trasferimento di un DAC non
monotono
D2
0
0
0
0
1
1
1
1
D1
0
0
1
1
0
0
1
1
D0
0
1
0
1
0
1
0
1
Vo/VR
0
0,125
0
0,125
0,5
0,625
0,5
0,625
0,70
0,60
0,50
V o/V R
NK
0
1
2
3
4
5
6
7
0,40
0,30
0,20
0,10
0,00
000
001
010
011
100
101
110
111
Codice di ingresso
Caso a): Deviatore S1 sempre a massa
NK
0
1
2
3
4
5
6
7
D2
0
0
0
0
1
1
1
1
D1
0
0
1
1
0
0
1
1
D0
0
1
0
1
0
1
0
1
Vo/VR
0,25
0,375
0,25
0,375
0,75
0,875
0,75
0,875
Vo/VR
Caratteristica di trasferimento di un DAC non
monotono
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
000
001
010
011
100
101
110
111
Codice di ingresso
Caso b): deviatore S1 sempre a VR
Commento
Il malfunzionamento produce un comportamento non monotono: l’uscita del DAC non cresce
sempre, ma talvolta decresce, al crescere del codice.